Subsections
Experimental evaluation
In this section, after explaining the setup for the experiments,
we describe the results.
In previous sections, we presented the optimal resource
allocation policy incorporated in CAM for monitoring changes in
pages relevant to continuous queries. Here we evaluate our policy
by comparing it with some classical policies using a synthetic data
set. These policies [3] are:
- Uniform
- in which resources (monitoring tasks) are allocated uniformly
across all pages, and
- Proportional
- in which resources are allocated proportional to
change-frequencies of pages respectively.
As suggested in [18], it would be fair
to compare with the weighted version of these policies than the
unweighted ones: In the Weighted Uniform scheme, the
number of monitoring tasks (xi) allocated to a page
depends on the weights (Wi) associated with the page
but is independent of its change frequency
(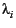 ):
xi
):
xi 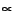 Wi. In the Proportional scheme,
xi
Wi. In the Proportional scheme,
xi 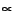
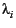 Wi.
As mentioned earlier, each page has an estimated change frequency
(
Wi.
As mentioned earlier, each page has an estimated change frequency
(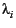 )
associated with it which denotes the expected number of changes
that occur in a page in time T.
Also, there is a sequence Ui of update instants (ui, j) for each page i which enumerates the time instants at
which changes can occur in it. With each update instant (ui, j), there is an
associated probability (
)
associated with it which denotes the expected number of changes
that occur in a page in time T.
Also, there is a sequence Ui of update instants (ui, j) for each page i which enumerates the time instants at
which changes can occur in it. With each update instant (ui, j), there is an
associated probability (
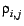 ) which
denotes the probability with which a change can occur at this
instant. To simplify our experiments, we make the sequence of
update instants (U) the same for
each page. At first sight, it seems to be in contrast with the
model we described in Section 2. There we said that each page
i may have its own distinct
sequence Ui. But note
that there is no loss of generality in fixing all update sequences
to a common U, if U is chosen as the union of
Uis of all pages, for
the following two reasons. First, the universal sequence U contains all possible update instants
of all the pages, so no update instant of any page is lost. Second,
we can mask off every update instant in U which does not occur in Ui by associating with it a
update probability of zero.
) which
denotes the probability with which a change can occur at this
instant. To simplify our experiments, we make the sequence of
update instants (U) the same for
each page. At first sight, it seems to be in contrast with the
model we described in Section 2. There we said that each page
i may have its own distinct
sequence Ui. But note
that there is no loss of generality in fixing all update sequences
to a common U, if U is chosen as the union of
Uis of all pages, for
the following two reasons. First, the universal sequence U contains all possible update instants
of all the pages, so no update instant of any page is lost. Second,
we can mask off every update instant in U which does not occur in Ui by associating with it a
update probability of zero.
Other experimental parameters are set as described below.
- Nq : The number of
queries submitted in the system, set to 500.
- N: The number of pages found
relevant the for the queries submitted. This is also set to 500.
This implies that set of relevant pages for queries have common
elements in them.
- C: The number of monitoring
tasks available. It is varied from 1000 to 50000 in our
experiments. If T is set to be 15
minutes (for example, the Google News site is said to use
crawlers which visit relevant sites every 15 minutes), then 50000
monitoring tasks would require a downloading speed of 56
documents/sec approximately.
- Change frequency distribution: The change frequencies
(
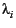 's) are
chosen according to a Zipf distribution with parameters
N and
's) are
chosen according to a Zipf distribution with parameters
N and 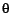 .
. 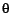 varies from 0 to 2. Such distributions
run the spectrum from highly skewed (when
varies from 0 to 2. Such distributions
run the spectrum from highly skewed (when 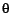 is 2) to uniform (when
is 2) to uniform (when 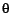 is 0). Unless otherwise
specified,
is 0). Unless otherwise
specified, 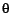 is set to 2 in experiments.
is set to 2 in experiments.
Figure 2: Change frequency
distribution
![\begin{figure}\begin{center} \includegraphics[scale=0.8]{freqDistGraph5bar} \end{center}\end{figure}](./img38.png)
|
- Update probability distribution: In our experiments,
we have 480 update instants in U
at uniform gaps throughout the duration T. For each experiment, we need to
associate a probability
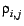 with
each update instant ui,
j. An actual update (or absence of an update) for page
i at the jth update instant is materialized by
tossing a coin with bias
with
each update instant ui,
j. An actual update (or absence of an update) for page
i at the jth update instant is materialized by
tossing a coin with bias
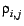 . For our
experiments, the probability values
. For our
experiments, the probability values
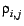 are
themselves generated from a Zipf distribution, clipped between 0
and 0.3. Using a Zipf distribution over
are
themselves generated from a Zipf distribution, clipped between 0
and 0.3. Using a Zipf distribution over
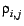 biases
them toward lower values and ensures that relatively few potential
update instants are likely to be instantiated into an actual update
for any page. Henceforth we will refer to this distribution as
update probability distribution. News sites are often
updated in a quasi-deterministic
manner: at specific intervals, changes occur with some probability.
This means the inter-update time distribution has multiple modes,
which can be modeled by generating many ``humps'' in their update
probability distribution, with probability varying in the vicinity
of every hump in Zipf fashion. Note that the probabilities
biases
them toward lower values and ensures that relatively few potential
update instants are likely to be instantiated into an actual update
for any page. Henceforth we will refer to this distribution as
update probability distribution. News sites are often
updated in a quasi-deterministic
manner: at specific intervals, changes occur with some probability.
This means the inter-update time distribution has multiple modes,
which can be modeled by generating many ``humps'' in their update
probability distribution, with probability varying in the vicinity
of every hump in Zipf fashion. Note that the probabilities
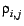 for all
update instants of a page should sum up to expected
change-frequency (
for all
update instants of a page should sum up to expected
change-frequency (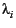 ) of that page. Also note that we
vary the Zipf skewness parameter of the update probability
distribution from 0 to 2 in our experiments and so we get a
corresponding update probability distribution for a page varying
from a uniform to a highly skewed distribution. All this makes our
experiments free from a priori assumptions about page change
behavior and helps in evaluating our policies for real
scenarios.
) of that page. Also note that we
vary the Zipf skewness parameter of the update probability
distribution from 0 to 2 in our experiments and so we get a
corresponding update probability distribution for a page varying
from a uniform to a highly skewed distribution. All this makes our
experiments free from a priori assumptions about page change
behavior and helps in evaluating our policies for real
scenarios.
- Weight of queries : All queries are assigned the same
importance measure (
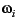 ). This means that there is no
distinction made among queries and they are defined to have equal
importance.
). This means that there is no
distinction made among queries and they are defined to have equal
importance.
- Page weight distribution: Recent studies [17] show that popularity of pages vary in
a Zipfian fashion as shown in Fig 3.
Figure 3: Observed
popularity distribution
![\begin{figure}\begin{center} \includegraphics[scale=0.8]{popularityEstimationbar} \end{center}\end{figure}](./img39.png)
|
Drawing an analogy, we choose ri,
j, the relevance of page j for a query i, from another Zipf distribution. There
is some evidence [19] that the
popularity of a page is positively related to its rate of updates.
Therefore, in our experiments, we make the more dynamic pages have
higher relevance. The summation of relevance measures of a page for
all the queries gives us the weight (Wi) for this page as
discussed in Section 3.
The distribution according to which Wi varies is referred to as
page weight distribution.
- Monitoring-change ratio: denotes the ratio of the
total number of monitoring tasks to
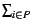
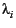 : the number of actual changes
expected in time T.
: the number of actual changes
expected in time T.
: The total expected information change over all pages is
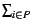 Wi
Wi 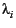 , and if the allocation algorithm
selects suitable (0/1) values of yi,
j, the expected fraction of information change made
visible to the user(s) is
, and if the allocation algorithm
selects suitable (0/1) values of yi,
j, the expected fraction of information change made
visible to the user(s) is
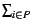 Wi.
Wi.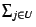
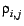 .yi, j. We define
the ratio of the latter to the former as the returned information ratio (RIR), our main
performance metric.
.yi, j. We define
the ratio of the latter to the former as the returned information ratio (RIR), our main
performance metric.
| RIR |
= |
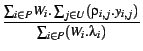 .
. |
|
Note that the maximum possible value of RIR is 1 and it is attained
by setting yi, j to 1
for every i, j having
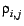 > 0.
This is the performance metric on the basis of which we compare
various allocation policies in our experiments.
> 0.
This is the performance metric on the basis of which we compare
various allocation policies in our experiments.
In this experiment, we evaluate the aforementioned resource
allocation polices and also observe the effects of update
probability distribution and page weight distribution on their
performance.
Uniform page weights and update
probabilities
We make both these distributions uniform and set the Zipf
parameter of change frequency distribution to 2 as shown in
Figure 2.
Uniform page weight distribution means that all pages have equal
importance while uniform update probability distribution leads to
equal probability of change to a page at any update instant
in T.
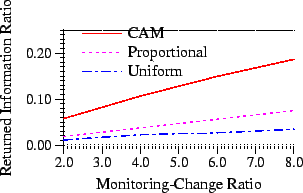
Figure 4: Performance
under uniform page weight and update probability
distribution
|
Figure 4
shows the performance of different resource allocation policies.
There are two important observations.
- The proportional policy performs better than its uniform
counterpart. This is very surprising as earlier studies showed the
reverse to be true [3,18]. The reason becomes clear when we
delve into the nature of the crawling vs. the monitoring problem.
In our case, we answer continuous queries and our aim is to detect
as many changes as possible. So when all other parameters
(page-weight and update probability distribution) are uniform, one
would certainly expect more benefits by monitoring those pages
which have high change frequency (
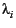 ) because these pages have
considerable chances of changing. This is what the proportional
policy does and so it performs better than the uniform policy.
Earlier studies solved the (convex optimization) problem of
answering discrete queries and aimed to maximize freshness
of pages. In that problem domain, the performance of the uniform
policy was better than the proportional policy. We offer a formal
proof of why uniform does not work as well as proportional for
continuous queries in Appendix A.
) because these pages have
considerable chances of changing. This is what the proportional
policy does and so it performs better than the uniform policy.
Earlier studies solved the (convex optimization) problem of
answering discrete queries and aimed to maximize freshness
of pages. In that problem domain, the performance of the uniform
policy was better than the proportional policy. We offer a formal
proof of why uniform does not work as well as proportional for
continuous queries in Appendix A.
Figure 5: Characteristics
of Resource Allocation Policies
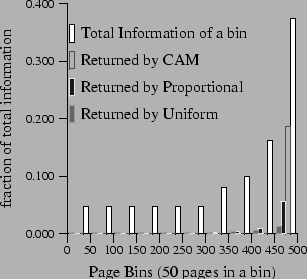
|
- The optimal policy also allocates more monitoring tasks to more
dynamic pages but it does it even more aggressively than the
proportional policy. Figure 5 shows that CAM allocates all its
monitoring tasks to only a few pages (for clarity, for the sake of
this graph, 50 pages of consecutive page indices have been grouped
into a bin) and delivers most of the change information from these
pages to CQs. The pages monitored are those which have high
probability of actually changing. Proportional does this too, but,
as its name indicates, it can only allocate tasks in a proportional
manner, while CAM does it in a more biased fashion and get even
better performance. It is evident from the graph that optimal
policy performs 300% better than the proportional policy and around
600% better than the uniform policy.
If we decrease the skewness (the Zipf parameter of the change
frequency distribution), the policies start approaching each other.
In the extreme case, they all become the same when frequencies are
made to be distributed in a uniform manner (Zipf parameter set to
0).
Skewed page update probabilities
We skew the update probability distribution with Zipf parameter
set to 1. So all pages are still of equal importance, but for
each page, the probability that an update instant instantiates to
an actual update is no longer the same for all update instants.
Figure 6
shows the performance in this setting. Again, CAM performs best
leaving other allocation policies far behind. It is 12 times better
than the uniform policy. But in this case, the pages which are
monitored by CAM turn out to be quite diversified as pages with
even lower change frequency have some update instants with a good
chance of actually changing, as shown in Figure 7.
Figure 6: Under skewed
update probability and uniform page weight distribution
![\begin{figure}\begin{center} \includegraphics[]{uniformWeightGraph} \end{center}\end{figure}](./img44.png)
|
Figure 7: Characteristics
of resource allocation policies
![\begin{figure}\begin{center} \includegraphics[]{bar2} \end{center}\end{figure}](./img45.png)
|
When page weights are skewed
If we make page-weight distribution skewed while keeping update
probability distribution uniform, we find that Optimal again
performs far better than others, as shown in Figure 8. Also, now it
allocates monitoring tasks to those pages which have high
importance and a higher probability of getting changed.
Figure 8: Performance
under skewed page weight and uniform update probability
distribution
![\begin{figure}\begin{center} \includegraphics[]{uniformProbGraph} \end{center}\end{figure}](./img46.png)
|
In summary, CAM's resource allocation approach performs better
than the previously proposed uniform and proportional approaches
across a wide spectrum of distributions. In particular, the more
skewed the distributions, the more pronounced the performance
improvement.
Figure 9 compares
performance of different resource allocation policies when
monitoring-to-change ratio![[*]](./footnote.png) is kept at 9 and the page
weight distribution is uniform.
is kept at 9 and the page
weight distribution is uniform.
Figure 9: Performance
under varying skewness of update probability distribution
![\begin{figure}\begin{center} \includegraphics[]{upograph1} \end{center}\end{figure}](./img47.png)
|
It is clear that for this data set, CAM's resource allocation
policy always performs better than the other resource allocation
policies. To emphasize the difference, we varied the update
probability distribution keeping other parameters the same as
before. As is evident from Figure 9, CAM's resource allocation
policy starts performing even better than other policies as update
distribution is made more and more skewed. It exhibits a 5-fold
improvement over uniform resource allocation policy when the Zipf
parameter is 0, and a 10-fold improvement when the Zipf parameter
is 1.5. This is because CAM monitors pages preferentially at
those update instants which have a high probability of returning
relevant information. As the update probability distribution is
made more and more skewed, CAM responds to the skewness by
selecting the most beneficial instants for monitoring, thus
performing even better than before. The uniform and proportional
policies do not take into account the granularity of update
instants and decide to monitor based on weight and change
frequency. (Note that when the Zipf parameter is set to zero, it
does not mean that update probabilities become uniformly
distributed, instead of this it means that all update probability
values occur equal number of times.)
In the previous experiment, we observed that even when we have
nine times more monitoring tasks available than expected number of
changes, the loss of information remains significant. This is
because of the distributed and uncertain nature of page change
behavior which make the number of monitoring tasks required for
good performance very large (Section 5.2.1). In the ideal case,
we will require continuous monitoring of web pages. Even a large
number of monitoring tasks (until they become comparable the to
number of update instants) will not be of much help.
Figure 10: Performance
with varying skewness of update probability distribution
![\begin{figure}\begin{center} \includegraphics[]{comparisonOf567} \end{center}\end{figure}](./img48.png)
|
Figure 10
shows how performance varies with the update probability
distribution of page change behavior. It is also evident that pages
with almost uniform update probability distribution will require
more monitoring than the skewed case. Luckily, the Web is not
updated with a flat distribution. A recent measurement study by
Fetterly and others [6] showed that
most web pages do not change much, and that a page's previous
change rate is a good predictor of its future change rate. This
means that the most favorable scenario for CAM is, in fact,
reality.
Figure 11: Performance
with different skewness of page weight distribution
![\begin{figure}\begin{center} \includegraphics[]{varP} \end{center}\end{figure}](./img49.png)
|
We find that page weight distribution also affects the
performance in a significant way. This is intuitive: if we can
somehow figure out during the tracking phase that a particular set
of pages is serving a major part of reporting to users for
answering query, then we can improve our performance by assigning
them a major share of monitoring tasks. Figure 11 shows the effect of page-weight
distribution on the performance of allocation techniques. Extending
CAM to take advantage of further meta-information about the change
behavior of web pages will help respond to CQs even more
efficiently, and is left for future work.
Figure 12: Performance of
optimal policy
![\begin{figure}\begin{center} \includegraphics[]{resultsInVariationCrawlingRatio5Ext} \end{center}\end{figure}](./img50.png)
|
Here we evaluate the practical application of our proposed
scheme. As evident from Figure 12,
90% of the Information is returned in our technique when
monitor-change ratio is 20.
Without using CAM, retrieving 90% of the information would
require monitoring of at least 432 instants while CAM needs only 20
monitoring tasks (5% of the maximum needed monitoring tasks) .
Figure 13: Effect of
Resource Reallocation after every epoch
![\begin{figure}\begin{center} \includegraphics[]{variationofPerfWithRuns3} \end{center}\end{figure}](./img51.png)
|
While describing CAM, we mentioned that after every epoch of
length T, page change statistics
are updated and resource allocation decisions reevaluated for the
next epoch. This process may become very expensive, especially if
T is small. Therefore, we next
study the effect of the resource allocation delay to determine how
often it might be beneficial to reallocate the resources.
We start with page update probability distribution's Zipf
parameter set to 1. Then we generate an actual event based on this
update probability distribution by tossing a biased coin at every
update instant and declaring a change at an instant if it turns up
heads.
Figure 14: Effect of
Varying the Resource Reallocation Delay
![\begin{figure}\begin{center} \includegraphics[]{variationofPerfWithRunsDelay} \end{center}\end{figure}](./img52.png)
|
Before the next epoch, we modify the update probability
distribution based on the recent epoch by modifying update
probabilities (
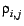 ) of
those update instants which get monitored in the epoch. We do this
modification simply by estimating the average rate of occurrence of
updates: if a page was updated five times in the last 10 monitoring
instants, the probability of expecting a change at the next update
instant is simply set to 0.5.
) of
those update instants which get monitored in the epoch. We do this
modification simply by estimating the average rate of occurrence of
updates: if a page was updated five times in the last 10 monitoring
instants, the probability of expecting a change at the next update
instant is simply set to 0.5.
Then we reallocate resources accommodating this new update
probability distribution. As Figure 13 shows,
performance of such a reallocation policy does increase in the
initial epochs and then becomes steady. This is what one would
expect because after a large number of epochs, the update
probability distribution itself becomes steady.
We also plotted two more graphs, as shown in Figure 14, to study
the effect of delayed resource allocation. Here the statistics are
updated after several epochs. We find
that it is not necessary to recompute resource allocation after
every epoch; it can be delayed without incurring any significant
loss provided the tracking phase was used to capture the initial
page change behavior. This study shows that it is possible to adapt
to the change behavior using the CAM approach and derive additional
benefits in terms of the quality of information returned.
In this experiment, we test our scheduling algorithm and show
its performance. The Zipf parameter of the change frequency
distribution is set to 2 and that of the update probability
distribution is set to 1.
Figure 15: Size of web
documents
![\begin{figure}\begin{center} \includegraphics[]{DocSizes} \end{center}\end{figure}](./img53.png)
|
Sizes of the documents are generated as shown in Figure 15 [9]. Also, the more popular pages' sizes are
set to be smaller [5]. We define
the average monitoring capacity as the
available bandwidth divided by average size of documents.
As shown in Figure 16, our scheduling
algorithm performs very well, usually accommodating all desired
monitoring tasks recommended by the resource allocation phase, when
the number of monitoring tasks is less than the average monitoring
capacity. Even when the number of monitoring tasks required to be
scheduled exceeds the average monitoring capacity, the loss of
information incurred in the scheduling phase remains quite
negligible in comparison to the resource allocation phase. The two
kinds of losses incurred are:
- As the number of monitoring tasks to be scheduled becomes more
than the average monitoring capacity, some tasks remain undone and
so some loss of information occurs.
- As number of monitoring tasks increases, the chances of
exceeding the monitoring capacity at any time also becomes high. So
these monitoring tasks get delayed, leading to loss of
information.
Figure 16: Allocation vs.
scheduling decisions.
![\begin{figure}\begin{center} \includegraphics[]{schComparison} \end{center}\end{figure}](./img54.png)
|
The experimental results lead to the following observations:
- CAM produces query results with higher coherency than either
Proportional or Uniform policies. Often the amount of returned
information with CAM's approach is 5-10 times that returned by
Uniform or Proportional. The more skewed the page update and page
weight distribution, the better the improvement. Increased
availability of monitoring resources (as indicated by the
monitoring-to-change ratio) also leads to a larger performance
improvement with CAM than with other approaches.
- By deploying a relatively small number of monitoring tasks,
e.g., 5% of the total number of update instants, CAM's resource
allocation and scheduling algorithms are able to return a very
large proportion, in the above case, 90%, of the changed
information.
- It is possible to improve performance further by updating the
page change statistics using of the changes monitored during each
epoch. We showed that in fact, it is possible to achieve
considerable performance improvement even if such adaptation is not
done after every epoch, but once after several epochs
suffices.
Sandeep Pandey 2003-03-05
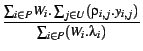 .
.![[*]](./footnote.png) is kept at 9 and the page
weight distribution is uniform.
is kept at 9 and the page
weight distribution is uniform.![]() ) of
those update instants which get monitored in the epoch. We do this
modification simply by estimating the average rate of occurrence of
updates: if a page was updated five times in the last 10 monitoring
instants, the probability of expecting a change at the next update
instant is simply set to 0.5.
) of
those update instants which get monitored in the epoch. We do this
modification simply by estimating the average rate of occurrence of
updates: if a page was updated five times in the last 10 monitoring
instants, the probability of expecting a change at the next update
instant is simply set to 0.5.