Next: Experimental evaluation Up: Monitoring the Dynamic Web Previous: Resource Allocation in CAM
As mentioned earlier, our goal is to schedule the allocated monitoring tasks among M parallel monitoring processes with the aim of minimizing the total delay between the ideal time instants and the actual scheduled time instants when a monitoring task must be executed.
Let page i be allocated xi number of monitoring tasks
in an optimal resource allocation. Also, suppose the time instants
at which these xi
monitoring tasks should be employed are
t1, t2,
t3,..., txi, as
identified in the resource allocation phase. Let
![]() be the average
fetching time for the
ith page. The
scheduling problem can be easily mapped to parallel shop scheduling
problem. In this problem, each job has to be processed on
exactly one of M identical
machines. Each monitoring task could be regarded as a
job whereas the monitoring processes are equivalent to
machines. Suppose there are a total of n such jobs. In scheduling problems, the
time at which a job becomes available for processing is called the
release time (
be the average
fetching time for the
ith page. The
scheduling problem can be easily mapped to parallel shop scheduling
problem. In this problem, each job has to be processed on
exactly one of M identical
machines. Each monitoring task could be regarded as a
job whereas the monitoring processes are equivalent to
machines. Suppose there are a total of n such jobs. In scheduling problems, the
time at which a job becomes available for processing is called the
release time (
![]() ) and the time for
which it needs a machine is called the processing time. So
in our case, ideal monitoring time instants
t1, t2,
t3,..., txi would be the
release times and fetching times of pages correspond to
processing times (pj)
for jobs. Our goal is to minimize the delay di between ideal monitoring
time instant
) and the time for
which it needs a machine is called the processing time. So
in our case, ideal monitoring time instants
t1, t2,
t3,..., txi would be the
release times and fetching times of pages correspond to
processing times (pj)
for jobs. Our goal is to minimize the delay di between ideal monitoring
time instant
![]() and actual time
instant si of
scheduling. In our case all the jobs are equally important as there
is no weight assigned with each monitoring. So our problem
can be formulated in scheduling notation as
and actual time
instant si of
scheduling. In our case all the jobs are equally important as there
is no weight assigned with each monitoring. So our problem
can be formulated in scheduling notation as
![]() (
(
![]() denotes the completion
time for job j), meaning that
R jobs of non-trivial release
times are available for scheduling at M machines with goal of minimizing the
average completion time. Minimizing the average completion time
leads to minimization of average delay time, because the total
completion time is
denotes the completion
time for job j), meaning that
R jobs of non-trivial release
times are available for scheduling at M machines with goal of minimizing the
average completion time. Minimizing the average completion time
leads to minimization of average delay time, because the total
completion time is
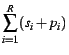 |
|||
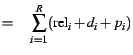
|
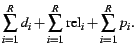
|
As
![]() and
and
![]() pi are
constants, minimizing average completion time is same as minimizing
delay time. Note that
pi are
constants, minimizing average completion time is same as minimizing
delay time. Note that
![]() is the same as si + pi because of
non-preemptive scheduling. Unfortunately even the simpler
problem
R| 1| relj
is the same as si + pi because of
non-preemptive scheduling. Unfortunately even the simpler
problem
R| 1| relj![]() 0|
0|![]() Cmj has been proved
to be NP-Complete [11]. So we
have to look for approximation algorithms. For completion
time problem there is an 1.58-approximation algorithm [11] which we used in our experiments as a
heuristic for optimizing average delay time (an approximation for
average completion time does not necessarily translate to the same
approximation for average delay time; the latter is harder to
approximate).
Cmj has been proved
to be NP-Complete [11]. So we
have to look for approximation algorithms. For completion
time problem there is an 1.58-approximation algorithm [11] which we used in our experiments as a
heuristic for optimizing average delay time (an approximation for
average completion time does not necessarily translate to the same
approximation for average delay time; the latter is harder to
approximate).