Recall is a well established measure in information retrieval (IR) and
information extraction (IE) for evaluating the effectiveness of either
retrieving relevant documents or extracting relevant statements with
statements considered to be the smallest bits of information about
entities [5].
For information gathering (IG) or knowledge acquisition from the Web
[3,4]
- which can be modeled as a consecutive process of IR, IE and Information
Integration (II) - the actual goal is not to locate and extract all
appearances of relevant information, but to extract as much unique
information as possible, disregarding all similar or redundant
appearances. For domains with large portions of redundant information on
the Web, such as digital consumer products or news, the dominant part of
relevant information can be gathered even with low overall recall. As an
example, a domain-specific recall of ![]() would probably be enough for learning the information that Shizuka
Arakawa won the gold medal in figure skating at the Winter Olympic Games
20061.
would probably be enough for learning the information that Shizuka
Arakawa won the gold medal in figure skating at the Winter Olympic Games
20061.
Therefore, this paper argues to shift the attention from the redundant representation of information to the actual core information stripped off of all redundancy (Fig. 1).
In what follows, we consider relevance to be a binary decision. Similarly, we disregard the issue of conflicting information and assume two statements to either express the same information, and hence be redundant, or not.
 be the number of relevant
statements and
be the number of relevant
statements and 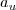 be the number of unique
statements among them, which is the smallest number of statements that
contain all relevant information or the core relevant information. We
define the term redundancy as
be the number of unique
statements among them, which is the smallest number of statements that
contain all relevant information or the core relevant information. We
define the term redundancy as

|
(1) |
 be the number of
unique statements within the total set of relevant statements, and let
be the number of
unique statements within the total set of relevant statements, and let
 be the number of gathered unique relevant statements,
stripped off of all redundandy. We define the terme unique recall
as
be the number of gathered unique relevant statements,
stripped off of all redundandy. We define the terme unique recall
as ) to be equal among
all subsets of relevant statements. Further assume the probability of
each occurrence of relevant information to be extracted by a given
mechanism equal and expressed by the measure recall (
) to be equal among
all subsets of relevant statements. Further assume the probability of
each occurrence of relevant information to be extracted by a given
mechanism equal and expressed by the measure recall ( can be approximated by
can be approximated by
|
|
|
|
Figure 2(a) shows equation 3 for example values of  . Despite the
apparent innocence of this formula, its derivation is not
straightforward. The proof succeeds by applying a limit value
consideration to a geometric model of a probabilistic lottery.
Figure 2(b) illustrates this
approximation to be suitable and to hold strongly for
. Despite the
apparent innocence of this formula, its derivation is not
straightforward. The proof succeeds by applying a limit value
consideration to a geometric model of a probabilistic lottery.
Figure 2(b) illustrates this
approximation to be suitable and to hold strongly for ![]() with
with ![]() being
the number of unique occurrences of relevant information.
being
the number of unique occurrences of relevant information.
By building on Proposition 1,
we can formulate the general equation for arbitrary redundancy
distributions with 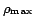 layers of
partly redundant information as
layers of
partly redundant information as
 being the fractions of the total amount of unique
information contained within a block with redundancy
being the fractions of the total amount of unique
information contained within a block with redundancy 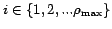 .
.
Calculating the first derivative and then taking the limit value for
![]() , we further
learn the approximation
, we further
learn the approximation
Figure 2(d) depicts equation 5 together with the closed solutions for the three canonical redundancy distributions homogeneous, linear and geometric from Fig. 2(c).
To demonstrate its practical relevance, assume we want to know the
fraction ![]() of available redundant
information instances we have to retrieve and extract in order to learn a
certain portion of the core information from a given domain of interest.
Further assume the redundancy distribution of information within this
domain to follow a known function
of available redundant
information instances we have to retrieve and extract in order to learn a
certain portion of the core information from a given domain of interest.
Further assume the redundancy distribution of information within this
domain to follow a known function 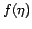 with
with ![$\eta \in[0,1]$](/www2006/pp209-gatterbauer-img31.png) and
and
 . The inverse function
. The inverse function
 of equation 4 then gives us the required joint
recall
of equation 4 then gives us the required joint
recall  of the IR and IE steps of our IG system.
of the IR and IE steps of our IG system.
Deriving a particular analytic solution is not always simple, mainly due
to the required transitions between discrete and continuous viewpoints.
However, given our derived approximation of  for
for ![]() from
equation 5, which holds even
stronger for
from
equation 5, which holds even
stronger for 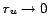 with
with
 , we can state the following approximation, independent
of the actual distribution
, we can state the following approximation, independent
of the actual distribution 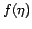 :
:
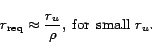
|
(6) |
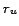 , and since we defined
, and since we defined
 as the average redundancy, this result seems to contrast
claims that the feature 'mean' has little practical value for skewed
distributions [1].
as the average redundancy, this result seems to contrast
claims that the feature 'mean' has little practical value for skewed
distributions [1].
The intriguing open and relevant problem is to derive the analytic
solution for a generalized Zipf redundancy distribution, as this
distribution is generally assumed to approximate well the frequency of
appearance of individual pieces of information on the Web [6,7]. A more playful
formulation of the research question is as follows: Assume the Zipf
distribution with exponential parameter
 of Fig. 2(c) adequately describes the redundancy
distribution of information on the Web [2]. What is the
generalization of the 20/80 rule [8] that holds for the
Web?
of Fig. 2(c) adequately describes the redundancy
distribution of information on the Web [2]. What is the
generalization of the 20/80 rule [8] that holds for the
Web?
Acknowledgement. The author would like to express his gratitude to
Professor Georg Gottlob for overall motivation of this research, and to
Konrad Richter for always having time to discuss some interesting
mathematical problems.