 |
(1) |
To address these differences among the users, there has been a recent surge of interest in personalized search to customize search results based on a user's interest. Given the large and growing importance of search engines, personalized search has the potential to significantly improve user experience. For example, according to recent statistics [3] if we can reduce the time users spend on searching for results on Google by a mere 1% through effective personalization, over 187,000 person-hours (21 years!) will be saved each month.
Unfortunately, studies have also shown that the vast majority of users are reluctant to provide any explicit feedback on search results and their interest [4]. Therefore, a personalized search engine intended for a large audience has to learn the user's preference automatically without any explicit input from the users. In this paper, we study the problem of how we can learn a user's interest automatically based on her past click history and how we can use the learned interest to personalize search results for future queries.
To realize this goal, there exist a number of important technical questions to be addressed. First, we need to develop a reasonable user model that captures how a user's click history is related to her interest; a user's interest can be learned through her click history only if they are correlated. Second, based on this model we need to design an effective learning method that identifies the user's interest by analyzing the user's click history. Finally, we need to develop an effective ranking mechanism that considers the learned interest of the user in generating the search result.
Our work, particularly our ranking mechanism, is largely based on a recent work by Haveliwala on Topic-Sensitive PageRank [5]. In this work, instead of computing a single global PageRank value for every page, the search engine computes multiple Topic-Sensitive PageRank values, one for each topic listed in the Open Directory1. Then during the query time, the search engine picks the most suitable Topic-Sensitive PageRank value for the given query and user, hoping that this customized version of PageRank will be more relevant than the global PageRank. In fact, in a small-scale user study, Haveliwala has shown that this approach leads to notable improvements in the search result quality if the appropriate Topic-Sensitive PageRank value can be selected by the search engine, but he posed the problem of automatic learning of user interest as an open research issue. In this paper, we try to plug in this final missing piece for an automatic personalized search system and make the following contributions:
The rest of this paper is organized as follows. We first provide an overview of Topic-Sensitive PageRank in Section 2, on which our work is mainly based. In Section 3 we describe our models and methods. Experimental results are presented in Section 4. We finally review related work in Section 5 and conclude the paper in Section 6.
 links to a page
links to a page 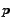 , it is probably because the author
of page
, it is probably because the author
of page  thinks that page
thinks that page 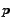 is important. Thus, this link adds
to the importance score of page
is important. Thus, this link adds
to the importance score of page  . How much score should be added
for each link? Intuitively, if a page itself is very important,
then its author's opinion on the importance of other pages is
more reliable; and if a page links to many pages, the importance
score it confers to each of them is decreased. This simple
intuition leads to the following formula of computing PageRank:
for each page
. How much score should be added
for each link? Intuitively, if a page itself is very important,
then its author's opinion on the importance of other pages is
more reliable; and if a page links to many pages, the importance
score it confers to each of them is decreased. This simple
intuition leads to the following formula of computing PageRank:
for each page  , let
, let
 denote the set of pages linking to
denote the set of pages linking to
 ,
,
 denote the number of out-links on page
denote the number of out-links on page
 , and
, and 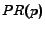 denote the PageRank of page
denote the PageRank of page
 ,
then
,
then
 |
(1) |
Another intuitive explanation of PageRank is based on the random surfer model [6], which essentially models a user doing a random walk on the web graph. In this model, a user starts from a random page on the web, and at each step she randomly chooses an out-link to follow. Then the probability of the user visiting each page is equivalent to the PageRank of that page computed using the above formula.
However, in real life, a user does not follow links all the
time in web browsing; she sometimes types URL's directly and
visits a new page. To reflect this fact, the random surfer model
is modified such that at each step, the user follows one of the
out-links with probability 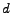 , while with the remaining
probability
, while with the remaining
probability  she gets bored and jumps to a new page. Under the
standard PageRank, the probability of this jump to a page is
uniform across all pages; when a user jumps, she is likely to
jump to any page with equal probability. Mathematically, this is
described as
she gets bored and jumps to a new page. Under the
standard PageRank, the probability of this jump to a page is
uniform across all pages; when a user jumps, she is likely to
jump to any page with equal probability. Mathematically, this is
described as
 for all
for all 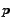 , where
, where  is the probability to
jump to page
is the probability to
jump to page  when she gets bored and
when she gets bored and  is the total number of web
pages. We call such a jump a random jump, and the vector
is the total number of web
pages. We call such a jump a random jump, and the vector
![$ \mathbf{E} = [E(1),\dots,E(n)]$](/www2006/main-img15.png) a random jump
probability vector. Thus we have the following modified
formula2:
a random jump
probability vector. Thus we have the following modified
formula2:
The computed PageRank values are used by search engines during query processing, such that the pages with high PageRank values are generally placed at the top of search results.
Note that under the standard PageRank, every page is assigned a single global score independently of any query. Therefore, PageRank can be deployed very efficiently for online query processing because it can be precomputed offline before any query. However, because all pages are given a single global rank, this standard PageRank cannot incorporate the fact that the relative importance of pages may change depending on a query.
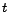 , we first define a biased
random jump probability vector with respect to topic
, we first define a biased
random jump probability vector with respect to topic
 ,
,
![$ \mathbf{E}_t = [E_t(1),\dots,E_t(n)]$](/www2006/main-img18.png) , as
, as
 is the total number of pages related to topic
is the total number of pages related to topic
 . The set of pages that are considered related to topic
. The set of pages that are considered related to topic
 (i.e., the pages whose
(i.e., the pages whose 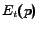 value is non-zero) are
referred to as the bias set of topic
value is non-zero) are
referred to as the bias set of topic  . Then the TSPR
score of page
. Then the TSPR
score of page  with respect to
with respect to 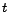 is defined as
is defined as
Note the similarity of Equations 2 and 4. Under the random surfer model
interpretation, the biased vector
 means that when a user jumps, she jumps only
to the pages related to topic
means that when a user jumps, she jumps only
to the pages related to topic 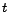 . Then
. Then  is equivalent to
the probability of the user's arriving at
is equivalent to
the probability of the user's arriving at  when her random
jumps are biased this way.
when her random
jumps are biased this way.
Assuming that we consider 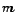 topics,
topics,  TSPR scores are
computed for each page, which can be done offline. Then during
online query processing, given a query, the search engine figures
out the most appropriate TSPR score and uses it to rank
pages.
TSPR scores are
computed for each page, which can be done offline. Then during
online query processing, given a query, the search engine figures
out the most appropriate TSPR score and uses it to rank
pages.
In [5], Haveliwala computed TSPR values considering the first-level topics listed in the Open Directory and showed that TSPR provides notable performance improvement over the standard PageRank if the search engine can effectively estimate the topic to which the user-issued query belongs. In the paper, the author also posed the problem of automatic identification of user preference as an open research issue, which can help the search engine pick the best TSPR for a given query and user.
In Section 3.1 we first describe our representation of user preferences. Then in Section 3.2 we propose our user model that captures the relationship between users' preferences and their click history. In Section 3.3 we proceed to how we learn user preferences. Finally in Section 3.4 we describe how to use this preference information in ranking search results.
Given the billions of pages available on the web and their diverse subject areas, it is reasonable to assume that an average web user is interested in a limited subset of web pages. In addition, we often observe that a user typically has a small number of topics that she is primarily interested in and her preference to a page is often affected by her general interest in the topic of the page. For example, a physicist who is mainly interested in topics such as science may find a page on video games not very interesting, even if the page is considered to be of high quality by a video-game enthusiast. Given these observations, we may represent a user's preference at the granularity of either topics or individual web pages as follows:
 -tuple
-tuple
![$ \mathbf{T} = [T(1), \dots, T(m)]$](/www2006/main-img27.png) , in which
, in which  is the
number of topics in consideration and
is the
number of topics in consideration and  represents the
user's degree of interest in the
represents the
user's degree of interest in the  topic (say,
``Computers''). The vector
topic (say,
``Computers''). The vector
 is normalized such that
is normalized such that
 .
.
![$ [0.75, 0.25]$](/www2006/main-img32.png) .
.
Instead of the above, we may represent a user's interest at the level of web pages.
 -tuple
-tuple
![$ \mathbf{P} = [P(1),\dots,P(n)]$](/www2006/main-img33.png) , in which
, in which  is the
total number of web pages and
is the
total number of web pages and  represents the user's
degree of interest in the
represents the user's
degree of interest in the 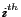 page. The vector
page. The vector
 is normalized such that
is normalized such that
 .
.
In principle, the page preference vector may capture a user's interest better than the topic preference vector, because her interest is represented in more detail. However, we note that our goal is to learn the user's interest through the analysis of her past click history. Given the billions of pages available on the web, a user can click on only a very small fraction of them (at most hundreds of thousands), making the task of learning the page preference vector very difficult; we have to learn the values of a billion-dimension vector from hundreds of thousands data points, which is bound to be inaccurate. Due to this practical reason, we use the topic preference vector as our representation of user interest in the rest of this paper.
We note that the this choice of preference representation is valid only if a user's interest in a page is mainly driven by the topic of the page. We will try to check the validity of this assumption later in the experiment section -- even though in an indirect way -- by measuring the effectiveness of our search personalization method based on topic preference vectors.
In Table 1, we summarize the symbols that we use throughout this paper. The meaning of some of the symbols will be clear as we introduce our user model.
 . Under the topic-driven random surfer model,
the user browses the web in a two-step process. First, the user
chooses a topic of interest
. Under the topic-driven random surfer model,
the user browses the web in a two-step process. First, the user
chooses a topic of interest 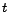 for the ensuing sequence of
random walks with probability
for the ensuing sequence of
random walks with probability  (i.e., her degree of
interest in topic
(i.e., her degree of
interest in topic 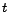 ). Then with equal probability,
she jumps to one of the pages on topic
). Then with equal probability,
she jumps to one of the pages on topic  (i.e, pages whose
(i.e, pages whose
 values are non-zero). Starting from this page,
the user then performs a random walk, such that at each step,
with probability
values are non-zero). Starting from this page,
the user then performs a random walk, such that at each step,
with probability 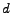 , she randomly follows an
out-link on the current page; with the remaining probability
, she randomly follows an
out-link on the current page; with the remaining probability
 she gets bored and picks a new topic of interest
for the next sequence of random walks based on
she gets bored and picks a new topic of interest
for the next sequence of random walks based on
 and jumps to a page on the chosen topic.
This process is repeated forever.
and jumps to a page on the chosen topic.
This process is repeated forever.
![$ [0.7, 0.3]$](/www2006/main-img41.png) . Under the topic-driven random surfer model,
this means that 70% of the the user's ``random-walk sessions''
(the set of pages that the user visits by following links)
start from computer-related pages and 30% start from
news-related pages. Note the difference of this model from the
standard random surfer model, where the user's random walk may
start from any page with equal probability.
. Under the topic-driven random surfer model,
this means that 70% of the the user's ``random-walk sessions''
(the set of pages that the user visits by following links)
start from computer-related pages and 30% start from
news-related pages. Note the difference of this model from the
standard random surfer model, where the user's random walk may
start from any page with equal probability.
Given this model and the discussion in Section 2.2, we can see that ,  ,
the Topic-Sensitive PageRank of page
,
the Topic-Sensitive PageRank of page  with regard to topic
with regard to topic
 , is equivalent to the probability of a user's visiting
page
, is equivalent to the probability of a user's visiting
page  when the user is only interested in topic
when the user is only interested in topic  (i.e.,
(i.e.,
 is 1 for
is 1 for 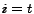 and 0 otherwise).
and 0 otherwise).
In general, we can derive the relationship between a user's
visit to a page and her topic preference vector
 . To help the derivation, we first define a
user's visit probability vector
. To help the derivation, we first define a
user's visit probability vector
 -tuple
-tuple
![$ \mathbf{V} = [V(1), \dots, V(n)]$](/www2006/main-img43.png) , in which
, in which  is the
total number of pages and
is the
total number of pages and 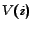 represents the user's
probability to visit the page
represents the user's
probability to visit the page  . We assume the vector
. We assume the vector
 is normalized such that
is normalized such that
 .
.
Given this definition, it is straightforward to derive the
following relationship between a user's visit probability vector
 and the user's topic preference vector
and the user's topic preference vector
 based on the linearity property of TSPR
[5]:
based on the linearity property of TSPR
[5]:
![$ \mathbf{T} = [T(1), \dots, T(m)]$](/www2006/main-img27.png) and the visit
probability vector
and the visit
probability vector
![$ \mathbf{V} = [V(1), \dots, V(n)]$](/www2006/main-img43.png) . Under the
topic-driven random surfer model,
. Under the
topic-driven random surfer model,  , the probability to
visit page
, the probability to
visit page  , is given by
, is given by
Note that Equation 5 shows the relationship between a user's visits and her topic preference vector if the user follows the topic-driven random surfer model. In practice, however, the search engine can only observe the user's clicks on its search result, not the general web surfing behavior of the user. That is, the user clicks that the search engine observes is not based on the topic-driven random surfer model; instead the user's clicks are heavily affected by the rankings of search results. To address this discrepancy, we now extend the topic-driven random-surfer model as follows:
 . Under the topic-driven searcher model, the
user always visits web pages through a search engine in a
two-step process. First, the user chooses a topic of interest
. Under the topic-driven searcher model, the
user always visits web pages through a search engine in a
two-step process. First, the user chooses a topic of interest
 with probability
with probability 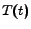 . Then the user goes to the
search engine and issues a query on the chosen topic
. Then the user goes to the
search engine and issues a query on the chosen topic
 . The search engine then returns pages ranked by
. The search engine then returns pages ranked by
 , on which the user clicks.
, on which the user clicks.
To derive the relationship between a user's visit probability
vector
 and her topic preference vector
and her topic preference vector
 under this new model, we draw upon the result
from a recent study by Cho and Roy [8]. In [8], the authors have shown that when a
user's clicks are affected by search results ranked by
under this new model, we draw upon the result
from a recent study by Cho and Roy [8]. In [8], the authors have shown that when a
user's clicks are affected by search results ranked by
 , the user's visit probability to page
, the user's visit probability to page  ,
,
 , is proportional to
, is proportional to
 , as opposed to
, as opposed to  as predicted by the
random-surfer model. Given this new relationship, it is
relatively straightforward to prove the following:
as predicted by the
random-surfer model. Given this new relationship, it is
relatively straightforward to prove the following:
 and the visit probability vector
and the visit probability vector
 . Then under the topic-driven searcher model,
. Then under the topic-driven searcher model,
 is given by3
is given by3
 is replaced with
is replaced with
![$ [TSPR_i(p)]^{9/4}$](/www2006/main-img57.png) , a replacement coming from the result
in [8].
, a replacement coming from the result
in [8].
In the rest of this paper, we will assume the above topic-driven searcher model as our main user model and use Equation 6 as the relationship between a user's visit probability vector and her topic preference vector.
 values
experimentally by observing the user's clicks on search results
as we illustrate in the following example:
values
experimentally by observing the user's clicks on search results
as we illustrate in the following example:
![$ \mathbf{V} = [\frac{2}{3}, \frac{1}{3}, 0, \dots, 0]$](/www2006/main-img58.png) given the click history.
given the click history.
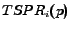 values in Equation
6 can be computed from Equation
4 based on the hyperlink
structure of the web and a reasonable choice of the bias set for
each topic. The only unknown variables in Equation 6 are
values in Equation
6 can be computed from Equation
4 based on the hyperlink
structure of the web and a reasonable choice of the bias set for
each topic. The only unknown variables in Equation 6 are 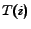 values, which can be derived
from other variables in the equation. Formally, this learning
process can be formulated as the following problem:
values, which can be derived
from other variables in the equation. Formally, this learning
process can be formulated as the following problem:
![$ \mathbf{V} = [V(1), \dots, V(n)]$](/www2006/main-img43.png) , and
, and  Topic-Sensitive PageRank vectors
Topic-Sensitive PageRank vectors
![$ \mathbf{TSPR}_i = [TSPR_i(1),\dots,TSPR_i(n)]$](/www2006/main-img59.png) for
for
 , find the user's topic preference vector
, find the user's topic preference vector
![$ \mathbf{T} = [T(1), \dots, T(m)]$](/www2006/main-img27.png) that satisfies
that satisfies
 to denote a vector whose elements are the
elements of
to denote a vector whose elements are the
elements of
 raised to the
raised to the  th power.
th power.
There exist a number of ways to approach this problem. In particular, regression-based and maximum-likelihood methods are two of the popular techniques used in this context:
 vector measured from user clicks cannot be
identical to the one prescribed by the model. Linear
regression is a popular method used in this scenario. It
picks the unknown parameter values such that the difference
between what we observe and what the model prescribes is
minimized. In our context, it determines the
vector measured from user clicks cannot be
identical to the one prescribed by the model. Linear
regression is a popular method used in this scenario. It
picks the unknown parameter values such that the difference
between what we observe and what the model prescribes is
minimized. In our context, it determines the  values that minimize the square-root error
values that minimize the square-root error
 .
Assuming that TSPR is an
.
Assuming that TSPR is an
 matrix whose
matrix whose  entry is
entry is
 , the linear regression method asserts
that this error is minimum when the topic preference vector
is
, the linear regression method asserts
that this error is minimum when the topic preference vector
is
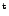 is the transpose
of TSPR.
is the transpose
of TSPR.
 pages and use
pages and use
 to denote the
to denote the 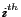 visited page. We also
define
visited page. We also
define
 as
as
 , the
probability that the user visits page
, the
probability that the user visits page  under the
topic-driven searcher model when her topic preference vector
is
under the
topic-driven searcher model when her topic preference vector
is
![$ \mathbf{T} = [T(1), \dots, T(m)]$](/www2006/main-img27.png) . Assuming that all
user visits are independent, the probability that the user
visits the pages
. Assuming that all
user visits are independent, the probability that the user
visits the pages
 is then
is then
 . Then the values
of the vector
. Then the values
of the vector
 is chosen such that this probability is
maximized. That is, under the maximum-likelihood estimator,
is chosen such that this probability is
maximized. That is, under the maximum-likelihood estimator,
In our experiments, we have applied both methods to the learning task and find that the maximum-likelihood estimator performs significantly better than the linear regression method. This is in large part due to, again, the sparsity of the observed click history. Since the user does not visit the vast majority of pages, most of the entries in the visit probability vector are zero. Therefore, even though two users may visit completely different sets of pages, the difference between their visit probability vectors is small because the two vectors have the same zero values for most entries. This problem turns out to be not very significant for the maximum likelihood method because it only considers the pages that the user visited during estimation as we can see from Equation 9. In our experiment section, therefore, we report only the results from the maximum-likelihood estimator.
 , we
identify the most likely topic of the query
, we
identify the most likely topic of the query  and use the TSPR
values corresponding to the identified topic. More precisely,
given
and use the TSPR
values corresponding to the identified topic. More precisely,
given  , we estimate
, we estimate
 , the probability that
, the probability that  is related to topic
is related to topic
 , and compute the ranking of page
, and compute the ranking of page  as follows:
as follows:
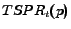 when the topic of the
query
when the topic of the
query  is clearly
is clearly 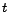 (i.e.,
(i.e.,
 only for
only for  ).
).
In deciding the likely topic of  , we may rely on two potential
sources of information: the user's preference and the
query itself.
, we may rely on two potential
sources of information: the user's preference and the
query itself.
 can be rewritten as
can be rewritten as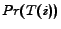 is the probability that the
user is interested in topic
is the probability that the
user is interested in topic 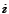 , which is captured in the
, which is captured in the
 term of the user's topic preference vector
term of the user's topic preference vector
![$ \mathbf{T} = [T(1), \dots, T(m)]$](/www2006/main-img27.png) . That is,
. That is,
 .
.
 is the probability that the user issues
the query
is the probability that the user issues
the query  when she is interested in topic
when she is interested in topic  . As in [5], this probability may be
computed by counting the total number of occurrences of terms in
query
. As in [5], this probability may be
computed by counting the total number of occurrences of terms in
query  in the web pages listed under the topic
in the web pages listed under the topic  in the
Open Directory.
in the
Open Directory.
Given Equations 10 and
11, we can then compute
 , the personalized ranking
of page
, the personalized ranking
of page  for query
for query 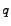 issued by the user of topic
preference vector
issued by the user of topic
preference vector
 , as follows:
, as follows:
 is the
personalization factor based on the user's preference.
is the
personalization factor based on the user's preference.
 is the term that identifies the topic
based on the query itself. Later in our experiment section, we
will evaluate the effectiveness of these two individual terms by
using only one of them during ranking.
is the term that identifies the topic
based on the query itself. Later in our experiment section, we
will evaluate the effectiveness of these two individual terms by
using only one of them during ranking.
 denotes the user's actual topic preference
vector and
denotes the user's actual topic preference
vector and
 denotes our estimation based on the
user's click history.
denotes our estimation based on the
user's click history.
![$\displaystyle \mathbf{TSPR}_{1} = \mathbf{TSPR}_{2} = [0.8, 0.1, 0, 0, 0.1].$](/www2006/main-img95.png) |
![$ \mathbf{T}_1 = [1,0]$](/www2006/main-img96.png) and
and
![$ \mathbf{T}_2 = [0,1]$](/www2006/main-img97.png) , respectively. In this
scenario, note that even though the users' topic preference
vectors are completely different, their visit probability
vectors are identical:
, respectively. In this
scenario, note that even though the users' topic preference
vectors are completely different, their visit probability
vectors are identical: |
 |
 |
|
 |
 |
Fortunately in this case, the difference in the weights of the topic preference vectors do not matter; the personalized ranking for the two users are always the same
 |
The above example illustrates that even though our
estimated topic preference vector may not be the same as the
user's actual vector, the final personalized ranking can
still be accurate, making our learning method useful. To
evaluate how well we can compute the user's personalized
ranking, we use the Kendall's  distance
[10] between our
estimated ranking and the ideal ranking.
That is, let
distance
[10] between our
estimated ranking and the ideal ranking.
That is, let 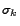 be the sorted list of
top-
be the sorted list of
top- pages based on the estimated personalized ranking
scores. Let
pages based on the estimated personalized ranking
scores. Let 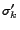 be the sorted
top-
be the sorted
top- list based on the the personalized ranking computed
from the user's true preference vector. Let
list based on the the personalized ranking computed
from the user's true preference vector. Let  be
the union of
be
the union of 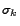 and
and  . Then the Kendall
. Then the Kendall  distance
between
distance
between  and
and 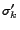 is computed as
is computed as
 |
(14) |
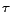 distance ranges between 0
and 1, taking 0 when the two ranks are identical. Given that
most users never look beyond the top 20 entries in search
results [1], using a
distance ranges between 0
and 1, taking 0 when the two ranks are identical. Given that
most users never look beyond the top 20 entries in search
results [1], using a
 value between 10 and 100 may be a good choice to
compare the difference in the ranks perceived by the users.
value between 10 and 100 may be a good choice to
compare the difference in the ranks perceived by the users.
In the next section, we evaluate the effectiveness of our personalized search framework using all three metrics described above.
To collect these data, we have contacted 10 subjects in the UCLA Computer Science Department and collected 6 months of their search history by recording all the queries they issued to Google and the search results that they clicked on. Table 2 shows some high-level statistics on this query trace.
To identify the set of pages that are relevant to queries, we carried out a human survey. In this survey, we first picked the most frequent 10 queries in our query trace, and for each query, each of the 10 subjects were shown 10 randomly selected pages in our repository that match the query. Then the subjects were asked to select the pages they found relevant to their own information need for that query. On average 3.1 (out of 10) search results were considered relevant to each query by each user in our survey.
Finally, we computed TSPR values for 500 million web pages collected in a large scale crawl in 2005. That is, based on the link structure captured in the snapshot, we computed the original PageRank and the Topic-Sensitive PageRank values for each of the 16 first-level topic listed in the Open Directory. The computation of these values was performed on a workstation equipped with a 2.4GHz Pentium 4 CPU and 1GB of RAM. The computation of 500 million TSPR values roughly took 10 hours to finish for each topic on the workstation.
The best way of measuring the accuracy of our method is to
estimate the users' topic preferences from the real-life data we
have collected, and ask the users how accurate our results are.
The problem with this method is that, although users could tell
which are the topics they are most interested in, it tends to be
very difficult for them to assign an accurate weight to each of
these topics. For example, if a user is interested in
``Computers'' and ``News,'' is her topic preference vector
![$ [0.5, 0.5]$](/www2006/main-img107.png) or
or
![$ [0.4, 0.6]$](/www2006/main-img108.png) ? This innate inaccuracy in users' topic
preference estimations makes it difficult to investigate the
accuracy of our method using real-life data.
? This innate inaccuracy in users' topic
preference estimations makes it difficult to investigate the
accuracy of our method using real-life data.
Thus, we will use a synthetic dataset generated by simulation based on our topic-driven searcher model:
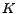 as an experimental parameter.
Then we randomly choose
as an experimental parameter.
Then we randomly choose 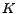 topics and assign random
weights to each selected topic. The weights for other topics
are set to 0. The vector is normalized to sum up to one.
topics and assign random
weights to each selected topic. The weights for other topics
are set to 0. The vector is normalized to sum up to one. clicks done by the user using the visit probability
distribution dictated by our model (Equation 6 in Section 3.2).
clicks done by the user using the visit probability
distribution dictated by our model (Equation 6 in Section 3.2).In order to measure the accuracy of the estimated topic
preference vector we generate synthetic user click traces as
described above and measure the relative error of our estimated
vector compared to the true preference vector (Equation 13). Figure 1 shows the results from this
experiment. In the graph, the height of a bar corresponds to the
average relative error at the given  and
and  values.
values.
From the figure, we see that at the same  value, as the
sample size
value, as the
sample size  increases, the relative error of our method
generally decreases. For instance, when
increases, the relative error of our method
generally decreases. For instance, when  , the relative
error at
, the relative
error at  is 0.66, but the error goes down to 0.46 when
is 0.66, but the error goes down to 0.46 when
 . For most
. For most 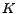 values, we also observe that
beyond the sample size
values, we also observe that
beyond the sample size 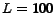 , the decreasing trend of the
relative error becomes much less significant. For example, when
, the decreasing trend of the
relative error becomes much less significant. For example, when
 , the relative error at
, the relative error at  is 0.4, but the error
actually gets slightly larger to 0.41 when
is 0.4, but the error
actually gets slightly larger to 0.41 when  . In the graph,
an interesting number to note is when
. In the graph,
an interesting number to note is when  and
and  , because this
is the setting that we expect to see in practical
scenarios.4At this parameter setting
(
, because this
is the setting that we expect to see in practical
scenarios.4At this parameter setting
( ,
,  ) the average relative error from our estimation
is 0.3, indicating that we can learn the user's topic preference
vector with 70% accuracy. The graph also shows that as the user
gets interested in more topics (i.e., as
) the average relative error from our estimation
is 0.3, indicating that we can learn the user's topic preference
vector with 70% accuracy. The graph also shows that as the user
gets interested in more topics (i.e., as  increases), the
accuracy of our method generally gets worse. This trend is
expected because when
increases), the
accuracy of our method generally gets worse. This trend is
expected because when 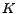 is large the user visits pages on
diverse topics. Therefore, we need to collect a larger number of
overall clicks, to obtain a similar number of clicks on the pages
on a particular topic.
is large the user visits pages on
diverse topics. Therefore, we need to collect a larger number of
overall clicks, to obtain a similar number of clicks on the pages
on a particular topic.
In Figure 2, we try to
see whether our estimation is meaningful at all by comparing it
against the baseline estimation, which assumes an equal weight
for every topic (i.e.,
 for
for
 ). The graph for our method is based on when
). The graph for our method is based on when
 . From the graph, we can see that when the users are
interested in a relatively few number of topics (
. From the graph, we can see that when the users are
interested in a relatively few number of topics (
 ), our estimate can be meaningful. The
relative error is significantly smaller than for the baseline
estimation, indicating that we do get to learn the user's general
preference. However, when the user interest is very diverse, the
graph shows that we need to collect much more user-click-history
data in order to obtain a meaningful estimate for the user
preference.
), our estimate can be meaningful. The
relative error is significantly smaller than for the baseline
estimation, indicating that we do get to learn the user's general
preference. However, when the user interest is very diverse, the
graph shows that we need to collect much more user-click-history
data in order to obtain a meaningful estimate for the user
preference.
We now investigate the accuracy of our personalized
ranking. To measure this accuracy, we again generate
synthetic user click data based on our model and estimate the
user's topic preference vector. We then compute the Kendall's
 distance between the ranking computed from the
estimated preference vector and the ranking computed
from the true preference vector. Figure 3 shows the results when the distance
is computed for the top 20 pages.5 We can see from the
figure that, in spite of the relatively large relative error
reported in the previous section, our method produces pretty good
rankings. For example, when
distance between the ranking computed from the
estimated preference vector and the ranking computed
from the true preference vector. Figure 3 shows the results when the distance
is computed for the top 20 pages.5 We can see from the
figure that, in spite of the relatively large relative error
reported in the previous section, our method produces pretty good
rankings. For example, when 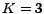 and
and  , the distance is
0.05, meaning that only 5% of the pairs in our ranking are
reversed compared to the true ranking.
, the distance is
0.05, meaning that only 5% of the pairs in our ranking are
reversed compared to the true ranking.
We now compare our personalized ranking against two other
baseline rankings: (1) a ranking based on general PageRank and
(2) a ranking based on Equation 12, but assuming that all topic
weights are equal (i.e.,
 for
for
 ). This comparsion will indicate how much
improvement we get from our topic preference estimation. In
Figure 4 we compare the
Kendall's
). This comparsion will indicate how much
improvement we get from our topic preference estimation. In
Figure 4 we compare the
Kendall's  distance of the three ranking methods for our
synthetic data. From the graph, we can see that our method
consistently produces much smaller distances than the two
baseline rankings, indicating the effectiveness of our learning
method.
distance of the three ranking methods for our
synthetic data. From the graph, we can see that our method
consistently produces much smaller distances than the two
baseline rankings, indicating the effectiveness of our learning
method.
 of Equation 12, but assuming that
of Equation 12, but assuming that
 for
for
 . This represents a ranking method that
does not take the user's preference into account.
. This represents a ranking method that
does not take the user's preference into account. . That is, we rank pages by
. That is, we rank pages by
 . This represents a
ranking method that uses the user preference, but not the query
in identifying the likely topic of the query.
. This represents a
ranking method that uses the user preference, but not the query
in identifying the likely topic of the query.In order to measure the quality of a ranking method, we use the data collected from the user survey described in Section 4.1. In the survey, for each of the 10 most common queries from our query trace, we asked our subjects to select the pages that they consider relevant to their own information need among 10 random pages in our repository that match the query. Considering that the queries chosen by us might not be the ones the users would issue in real life (and thus users may not care about the performance of our method on the queries), we also asked each subject to give the probability of her issuing each query in real life. Then for each of our subjects and queries, we compute the weighted average rank of the selected pages using the following formula under each ranking mechanism:
 |
(15) |
 denotes the set of pages the user
denotes the set of pages the user  selected for query
selected for query
 ,
,  denotes the probability that user
denotes the probability that user
 issues query
issues query 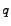 , and
, and  denotes the rank of
page
denotes the rank of
page  by the given ranking mechanism. Smaller AvgRank values
indicate better placements of relevant results, or better result
quality.
by the given ranking mechanism. Smaller AvgRank values
indicate better placements of relevant results, or better result
quality.
In Figure 5 we aggregate the results by queries to show how well our methods perform for different queries. The horizontal dotted lines in the graph show the average AvgRank over all queries. We can see that our personalization scheme is very effective and achieves significant performance improvement over traditional methods for most queries. The average improvements of Personalized PageRank and Query-Biased Personalized PageRank over Topic-Sensitive PageRank, over all queries, are 32.8% and 24.9%, respectively.6
We note that, from our experimental results, although the Query-Biased Personalized PageRank takes more information (both the user's topic preference and the query she issues) into consideration, it performs worse than Personalized PageRank in most cases. This result is quite surprising, but the difference is too small to draw a meaningful conclusion. It will be an interesting future work to see whether the Personalized PageRank indeed performs better than the Query-Biased Personalized PageRank in general and if it does, investigate the reason behind it.
In Figure 6 we
aggregate the results by participants to show the overall
effectiveness of our methods for each user. The horizontal dotted
lines in the graph show the average results of all participants.
We can see that the two personalization-based methods outperform
the traditional methods in all cases. For example, the
Personalized PageRank method outperforms Topic-Sensitive PageRank
by more than 70% for the 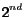 participant, while for the
participant, while for the
 participant the improvement is only around 7%.
This demonstrates that the effectiveness of personalization
depends on the user's search habits. For example, if the user is
not likely to issue ambiguous queries, then Topic-Sensitive
PageRank should be able to capture her search intentions pretty
well, thus decreasing the improvement our methods could achieve.
Nevertheless, our methods still greatly improve over the
traditional ones overall. The average improvements of
Personalized PageRank and Query-Biased Personalized PageRank over
Topic-Sensitive PageRank, over all participants, are 24.2% and
15.2%, respectively.
participant the improvement is only around 7%.
This demonstrates that the effectiveness of personalization
depends on the user's search habits. For example, if the user is
not likely to issue ambiguous queries, then Topic-Sensitive
PageRank should be able to capture her search intentions pretty
well, thus decreasing the improvement our methods could achieve.
Nevertheless, our methods still greatly improve over the
traditional ones overall. The average improvements of
Personalized PageRank and Query-Biased Personalized PageRank over
Topic-Sensitive PageRank, over all participants, are 24.2% and
15.2%, respectively.
![\includegraphics[width=3.6in]{by_subject.eps}](/www2006/main-img133.png)
|
Researchers have also proposed ways to personalize web search based on ideas other than PageRank [16,17,18]. For example, [16] extends the well-known HITS algorithm by artificially increasing the authority and hub scores of the pages marked ``relevant'' by the user in previous searches. [17] explores ways to consider the topic category of a page during ranking using user-specified topics of interest. [18] does a sophisticated analysis on the correlation between users, their queries and search results clicked to model user preferences, but due to the complexity of the analysis, we believe this method is difficult to scale to general search engines.
There also exists much research on learning a user's preference from pages she visited [19,20,21]. This body of work, however, mainly relies on content analysis of the visited pages, differently from our work. In [19], for example, multiple TF-IDF vectors are generated, each representing the user's interests in one area. In [20] pages visited by the user are categorized by their similarities to a set of pre-categorized pages, and user preferences are represented by the topic categories of pages in her browsing history. In [21] the user's preference is learned from both the pages she visited and those visited by users similar to her (collaborative filtering). Our work differs from these studies in that pages are characterized by their Topic-Sensitive PageRanks, which are based on the web link structure. It will be an interesting future work to develop an effective mechanism to combine both the content and the web link structure for personalized search.
Finally, Google7 has started a beta-testing of a new personalized search service8, which seems to estimate a searcher's interests from her past queries. Unfortunately, the details of the algorithm are not known at this point.
We have conducted both theoretical and real-life experiments to evaluate our approach. In the experiment on synthetic data, we found that for a reasonably small user search trace (containing 100 past clicks on results), the user interests estimated by our learning algorithm can be used to pretty accurately predict her view on the importance of web pages, which is expressed by her Personalized PageRank, showing that our method is effective and easily applicable to real-life search engines. In the real-life experiment, we applied our method to learn the interests of 10 subjects we contacted, and compared the effectiveness of our method in ranking future search results for them to traditional PageRank and Topic-Sensitive PageRank. The results showed that, on average, our method performed between 25%-33% better than Topic-Sensitive PageRank, which turned out to be much better than PageRank.
In the future we plan to expand our framework to take more user-specific information into consideration. For example, users' browsing behaviors, email information, etc. The difficulties in doing this include integration of different information sources, modeling of the correlation between various information and the user's search behavior, and efficiency concerns. We also plan to design more sophisticated learning and ranking algorithms to further improve the performance of our system.
[1] B.J. Jansen, A. Spink, and T Saracevic, Real life, real users, and real needs: A study and analysis of user queries on the Web, Information Processing and Management, 36(2):207 - 227, 2000.
[2] Robert Krovetz and W. Bruce Croft, Lexical ambiguity and information retrieval, Information Systems, 10(2):115-141, 1992.
[3] Nielsen netratings search engine ratings report, http://searchenginewatch.com/reports/article.php/2156461, 2003
[4] J. Carroll and M. Rosson, The paradox of the active user, Interfacing Thought: Cognitive Aspects of Human-Computer Interaction, 1987.
[5] T. Haveliwala, Topic-Sensitive PageRank, In Proceedings of the Eleventh Intl. World Wide Web Conf, 2002.
[6] S. Brin and L. Page, The anatomy of a large-scale hypertextual Web search engine, In Proc. of WWW '98, 1998.
[7] F. Qiu and J. Cho, Automatic identification of user preferences for personalized search, UCLA technical report, 2005.
[8] J. Cho and S. Roy, Impact of Web search engines on page popularity, In Proc. of WWW '04, 2004.
[9] Dimitri P. Bertsekas and John N. Tsitsiklis, Introduction to Probability, Athena Scientific, 2002.
[10] M. Kendall and J. Gibbons, Rank Correlation Methods, Edward Arnold, London, 1990.
[11] L. Page, S. Brin, R. Motwani, and T. Winograd, The PageRank citation ranking: Bringing order to the Web, Technical report, Stanford Digital Library Technologies Project, 1998.
[12] M. Richardson and P. Domingos, The Intelligent Surfer: Probabilistic Combination of Link and Content Information in PageRank, In Advances in Neural Information Processing Systems 14. MIT Press, 2002.
[13] G. Jeh and J. Widom, Scaling personalized web search,In Proceedings of the Twelfth Intl. World Wide Web Conf, 2003.
[14] S. Kamvar, T. Haveliwala, C. Manning, and G. Golub, Exploiting the block structure of the web for computing PageRank, Technical report, Stanford University, 2003.
[15] M. Aktas, M. Nacar, and F. Menczer, Personalizing PageRank based on domain profiles, In Proc. of WebKDD 2004: KDD Workshop on Web Mining and Web Usage Analysis, 2004.
[16] F. Tanudjaja and L. Mui, Persona: A contextualized and personalized web search, In Proc. of the 35th Annual Hawaii International Conference on System Sciences, 2002.
[17] P. Chirita, W. Nejdl, R. Paiu, and C. Kohlschuetter, Using ODP metadata to personalize search, In Proceedings of ACM SIGIR '05, 2005.
[18] J. Sun, H. Zeng, H. Liu, Y. Lu, and Z. Chen, CubeSVD: A novel approach to personalized web search, In Proceedings of the Fourteenth Intl. World Wide Web Conf, 2005.
[19] L. Chen and K. Sycara, Webmate: a personal agent for browsing and searching, Proc. 2nd Intl. Conf. on Autonomous Agents and Multiagent Systems, pages 132-139, 1998.
[20] A. Pretschner and S. Gauch, Ontology based personalized search, In ICTAI, pages 391-398, 1999.
[21] K. Sugiyama, K. Hatano, , and M. Yoshikawa, Adaptive web search based on user profile constructed without any effort from users, In Proceedings of the Thirteenth Intl. World Wide Web Conf, 2004.
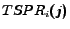 values are normalized
such that
values are normalized
such that
 , it may be that
, it may be that
 values do not satisfy
values do not satisfy
 . In Equation
5, we assume that we have
already renormalized
. In Equation
5, we assume that we have
already renormalized 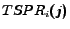 values such that
values such that
 for every
for every
 .
. pages for larger
pages for larger
 values and the results were similar.
values and the results were similar.