There is a general agreement that ``encoding some of the semantics of web resources in a machine processable form'' would allow designers to implement much smarter applications for final users, including information integration and interoperability, web service discovery and composition, semantic browsing, and so on. In a nutshell, this is what the Semantic Web is about. However, it is less obvious how such a result can be achieved in practice, possibly starting from the current web. Indeed, providing explicit semantic to already existing data and information sources can be extremely time and resource consuming, and may require skills that users (including web professionals) may not have.
Our work starts from the observation that in many Web sites,
web-based applications (such as web portals, e-marketplaces,
search engines), and in the file system of personal computers, a
wide variety of schemas (such as taxonomies, directory trees,
Entity Relationship schemas, RDF Schemas) are published which (i)
convey a clear meaning to humans (e.g. help in the navigation of
large collections of documents), but (ii) convey only a small
fraction (if any) of their meaning to machines, as their intended
meaning is not formally/explicitly represented. Well-known
examples are: classification schemas (or directories) used for
organizing and navigating large collections of documents,
database schemas (e.g. Entity-Relationship), used for describing
the domain about which data are provided; RDF schemas, used for
defining the terminology used in a collection of RDF statements.
As an example, imagine that a multimedia repository uses a
taxonomy like the one depicted in Figure 1 to classify pictures. For
humans, it is straightforward to understand that any resource
classified at the end of the path:
In the paper, we present a general methodology and an implementation to make this rich meaning available and usable by computer programs. This is a contribution to bootstrapping semantics on the Web, which can be used to automatically elicit knowledge from very common web objects. The paper has two main parts. In the first part we argue that, in making explicit the meaning of a schema, most approaches tend to focus on what we call structural meaning, but almost completely disregard (i) the linguistic meaning of components (typically encoded in the labels), and (ii) its composition with structural meaning; our thesis is that this approach misses the most important aspects of how meaning is encoded in schemas. The second part of the paper describes our method for eliciting meaning from schemas, and presents an implementation called CTXMATCH2. In conclusion, as an example of an application, we show how the results of this elicitation process can be used for schema and ontology matching and alignment.
Consider three very common types of schemas: hierarchical classifications (HCs), ER Schemas and RDF Schemas. Examples are depicted in Figures 2, 3 and 1.
They are used in different domains (document management, database design, vocabulary specification) to provide a structure which can be used to organize information sources. However, there is a second purpose which is typically overlooked, namely to provide humans with an easier access to those data. This is achieved mainly by labelling the elements of a schema with meaningful labels, typiclaly from some natural language. This is why, in our opinion, it is very uncommon to find a taxonomy (or an ER schema, or an RDF Schema specification) whose labels are meaningless for humans. Imagine, for example, how odd (and maybe hopeless) it would be for a human to navigate a classification schema whose labels are meaningless strings; or to read a ER schema whose nodes are labeled with random strings. Of course, humans would still be able to identify and use some formal properties of such schemas (for example, in a classification schema, we can always infer that a child node is more specific than its parent node, because this belongs to the structural understanding of a classification), but we would have no clues about what the two nodes are about. Similar observations can be made for the two other types of schemas. So, our research interest can be stated as follows: can we define a method which can be used to automatically elicit and represent the meaning of a schema in a form that makes available to machines the same kind of rich meaning which is available to humans when going through a schema?
We said that each node (e.g. in a HC) has an intuitive meaning
for humans. For example, the node ![]() in Figure 1 can
be easily interpreted as ``pictures of mountains in Tuscany'',
whereas
in Figure 1 can
be easily interpreted as ``pictures of mountains in Tuscany'',
whereas ![]() can be interpreted as
``color pictures of mountains in Trentino''. However, this
meaning is mostly implicit, and its elicitation may require a lot
of knowledge which is either encoded in the structure of the
schema, or must be extracted from external resources. In
[5], we
identified at least three distinct levels of knowledge which are
used to elicit a schema's meaning:
can be interpreted as
``color pictures of mountains in Trentino''. However, this
meaning is mostly implicit, and its elicitation may require a lot
of knowledge which is either encoded in the structure of the
schema, or must be extracted from external resources. In
[5], we
identified at least three distinct levels of knowledge which are
used to elicit a schema's meaning:
Most past attempts focused only on the first level. A recent example is [19], in which the authors present a methodology for converting thesauri into RDF/OWL; the proposed method is very rich from a structural point of view, but labels are disregarded, and no background domain knowledge is used. As to ER schemas, a formal semantics is defined for example in [4], using Description Logics; again, the proposed semantics is completely independent from the intuitive meaning of expressions used to label single components. For RDF Schemas, the situation is slightly different. Indeed, the common understanding is that RDFS schemas are used to define the meaning of terms, and thus their meaning is completely explicit; however, we observe that even for RDFS the associated semantics (see http://www.w3.org/TR/rdf-mt/) is purely structural, which means that there is no special interpretation provided for the labels used to name classes or other resources.
However, as we argued above through a few examples, labels (together with their organization in a schema) appear to be one of the main sources of meaning for humans. So we think that considering only structural semantics is not enough, and may lead to at least two serious problems:
The first issue can be explained through a simple example.
Suppose we have some method ![]() for making explicit the meaning of paths in HCs,
and that
for making explicit the meaning of paths in HCs,
and that ![]() does not take
the meaning of labels into account. Now imagine we apply
does not take
the meaning of labels into account. Now imagine we apply
![]() to the path
to the path
![]() -
-![]() in Figure 1,
and compare to a path like
in Figure 1,
and compare to a path like
![]() in
another schema (notice that typical HCs do not provide any
explicit information about edges in the path). Whatever
representation
in
another schema (notice that typical HCs do not provide any
explicit information about edges in the path). Whatever
representation ![]() is capable
of producing, the outcome for the two paths will be structurally
isomorphic, as the two paths are structurally isomorphic.
However, our intuition is that the two paths have a very
different semantic structure: the first should result is a term
where a class (``pictures'') is modified/restricted by two
attributes (``pictures of beaches located in
Tuscany''); the second is a standard Is-A hierarchy, where the
relation between the three classes is subsumption. The only way
we can imagine to explain this semantic (but not structural)
difference is by appealing to the meaning of labels. We grasp the
meaning of the first path because we know that pictures have a
subject (e.g. beaches), that beaches have a geographical
location, and that Tuscany is a geographical location. All this
is part of what we called lexical and domain knowledge. Without
it, we would not have any reason to consider ``pictures'' as a
class and ``Tuscany'' and ``beaches'' as values for attributes of
pictures. Analogously, we know that (a sense of the word) ``dog''
in English refers to a subclass of the class denoted by (a sense
of the word) ``mammals'' in English, and similarly for
``animals''.
is capable
of producing, the outcome for the two paths will be structurally
isomorphic, as the two paths are structurally isomorphic.
However, our intuition is that the two paths have a very
different semantic structure: the first should result is a term
where a class (``pictures'') is modified/restricted by two
attributes (``pictures of beaches located in
Tuscany''); the second is a standard Is-A hierarchy, where the
relation between the three classes is subsumption. The only way
we can imagine to explain this semantic (but not structural)
difference is by appealing to the meaning of labels. We grasp the
meaning of the first path because we know that pictures have a
subject (e.g. beaches), that beaches have a geographical
location, and that Tuscany is a geographical location. All this
is part of what we called lexical and domain knowledge. Without
it, we would not have any reason to consider ``pictures'' as a
class and ``Tuscany'' and ``beaches'' as values for attributes of
pictures. Analogously, we know that (a sense of the word) ``dog''
in English refers to a subclass of the class denoted by (a sense
of the word) ``mammals'' in English, and similarly for
``animals''.
The second issue is closely related to the first one. How do
we understand (intuitively) that
![]() refers to pictures
of beaches located in Tuscany, and not e.g. to
pictures working for Tuscany teaching beaches?
After all, the edges between nodes are not qualified, and
therefore any structurally possible relation is in principle
admissible. The answer is trivial: because, among other things,
we know that pictures do not work for anybody (but they
may have a subject), that Tuscany can't be the teacher of a beach
(but can be the geographical location of a beach). It is only
this body of background knowledge which allows humans to
conjecture the correct relation between the meanings of node
labels. If we disregard it, there is no special reason to prefer
one interpretation to the other.
refers to pictures
of beaches located in Tuscany, and not e.g. to
pictures working for Tuscany teaching beaches?
After all, the edges between nodes are not qualified, and
therefore any structurally possible relation is in principle
admissible. The answer is trivial: because, among other things,
we know that pictures do not work for anybody (but they
may have a subject), that Tuscany can't be the teacher of a beach
(but can be the geographical location of a beach). It is only
this body of background knowledge which allows humans to
conjecture the correct relation between the meanings of node
labels. If we disregard it, there is no special reason to prefer
one interpretation to the other.
The examples above should be sufficient to support the conclusion that any attempt to design a methodology for eliciting the meaning of schemas (basically, for reconstructing the intuitive meaning of any schema element into an explicit and formal representation of such a meaning) cannot be based exclusively on structural semantics, but must seriously take into account at least lexical and domain knowledge about the labels used in the schema5. The methodology we propose in the next section is an attempt to do this.
Intuitively, the problem of semantic elicitation can be viewed as the problem of computing and representing the (otherwise implicit) meaning of a schema in a machine understandable way. Clearly, meaning for human beings has very complex aspects, directly related to human cognitive and social abilities. Trying to reconstruct the entire and precise meaning of a term would probably be a hopeless goal, so our intuitive characterization must be read as referring to a reasonable approximation of meaning.
In our method, meanings are represented in a formal language
(called WDL, for WordNet Description Logic), which is the result
of combining two main ingredients: a logical language (in
this paper, use the logical language ![]() which belongs to the family of Description
Logics [2]), and
IDs of lexical entries in a dictionary (more specifically, from
WordNet [8], a well-known
electronic lexical database). Description logics are a family
logical languages that are defined starting from a set of
primitive concepts, relations and individuals, with a set of
logical constructors, and has been proved to provide a good
compromise between expressivity and computability. It is
supported with efficient reasoning services (see for instance
[14]);
WordNet is the largest and most shared online lexical resource,
whose design is inspired by psycholinguistic theories of human
lexical memory. WORDNET associates
with any word ``word'' a list of senses (equivalent to
entries in a dictionary), denoted as
which belongs to the family of Description
Logics [2]), and
IDs of lexical entries in a dictionary (more specifically, from
WordNet [8], a well-known
electronic lexical database). Description logics are a family
logical languages that are defined starting from a set of
primitive concepts, relations and individuals, with a set of
logical constructors, and has been proved to provide a good
compromise between expressivity and computability. It is
supported with efficient reasoning services (see for instance
[14]);
WordNet is the largest and most shared online lexical resource,
whose design is inspired by psycholinguistic theories of human
lexical memory. WORDNET associates
with any word ``word'' a list of senses (equivalent to
entries in a dictionary), denoted as
![]() , each
of which denotes a possible meaning of ``word''.
, each
of which denotes a possible meaning of ``word''.
The core idea of WDL is to use a DL language for representing
structural meaning, and any additional constraints (axioms) we
might have from domain knowledge; and to use
WORDNET to anchor the meaning of
labels in a schema to lexical meanings, which are listed and
uniquely identified as WORDNET
senses. Indeed, the primitives of any DL language do not have an
``intended'' meaning; this is evident from the fact that, as in
standard model-theoretic semantics, the primitive components of
DL languages (i.e. concepts, roles, individuals) are interpreted,
respectively, as generic sets, relations or individuals from some
domain. What we need to do is to ``ground'' their interpretation
to the WordNet sense that best represents their intended meaning
in the label. So, for example, a label like ![]() can be
interpreted as a generic class in a standard DL semantics, but
can be also assigned an intended meaning by attaching it to the
the first sense in WORDNET (which
in version 2.0 is defined as ``a body of (usually fresh) water
surrounded by land'').
can be
interpreted as a generic class in a standard DL semantics, but
can be also assigned an intended meaning by attaching it to the
the first sense in WORDNET (which
in version 2.0 is defined as ``a body of (usually fresh) water
surrounded by land'').
The advantage of WDL w.r.t. a standard DL encoding is that assigning an intended meaning to a label allows us to import automatically a body of (lexical) knowledge which is associated with a given meaning of a word used in a label. For example, from WORDNET we know that there is a relation between the class ``lakes'' and the class ``bodies of water'', which in turn is a subclass of physical entities. In addition, if an ontology is available where classes and roles are also lexicalized (an issue that here we do not address directly, but details can be found in [17]), then we can also import and use additional domain knowledge about a given (sense of) a word, for example that lakes can be holiday destinations, that Trentino has plenty of lakes, even that a lake called ``Lake Garda'' is partially located in Trentino, and so on and so forth.
Technically, the idea described above is implemented by using WORDNET senses as primitives for a DL language. A WDL language is therefore defined as follows:
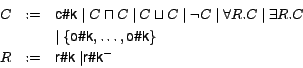
Some remarks are necessary.
Despite the fact that the intended semantics cannot be formally represented or easily determined by a computer, one should accept its existence and consider it at the same level as a ``potential'' WordNet sense. Under this hypothesis we can assume that expressions in WDL convey meanings, and can be used to represents meaning in a machine. Put it differently, since the WDL primitives represent common-sense concepts, then the complex concepts of WDL will also represent common-sense concepts, since common-sense concepts are closed under boolean operations and universal and existential role restriction.
From this perspective, the problem of semantic
elicitation can be thought of as the problem of finding a WDL
expression ![]() for each element
for each element
![]() of a schema, so that the
intuitive semantics of
of a schema, so that the
intuitive semantics of ![]() is a
good enough approximation of the intended meaning of the
node.
is a
good enough approximation of the intended meaning of the
node.
This section is devoted to the description of a practical semantic elicitation algorithm. This algorithm has been implemented as basic functionality of the CTXMATCH2 matching platform [17], and has been extensively tested in the 2nd Ontology Alignment Evaluation Initiative7.
In the following we will adopt the notation ![]() to denote the meaning
of a node
to denote the meaning
of a node ![]() .
. ![]() to denote the label of
the node, and
to denote the label of
the node, and ![]() or simply
or simply
![]() to denote the
meaning of a label associated with the node
to denote the
meaning of a label associated with the node ![]() considered out of its
context.
considered out of its
context. ![]() is also called
the local meaning.
is also called
the local meaning.
The algorithm for semantic elicitation is composed of three main steps. In the first step we use the structural knowledge on a schema to build a meaning skeleton. A meaning skeleton describes only the structure of a WDL complex concepts that constitutes the meaning of a node. In the second step, we fill nodes of with the appropriate concepts and individuals, using linguistic knowledge, and in the final step, we provide the roles, by exploiting domain knowledge.
Meaning skeletons are DL descriptions together with a set of
axioms. The basic components of a meaning skeleton (i.e. the
primitive concepts and roles) are the meanings of the single
labels associated with nodes, denoted by ![]() ), and the semantic relations between different
nodes (denoted by
), and the semantic relations between different
nodes (denoted by ![]() ).
Intuitively
).
Intuitively ![]() represents a
semantic relation between the node
represents a
semantic relation between the node ![]() and the node
and the node ![]() .
In the rest of this section we show how the meaning skeletons of
the types of schema considered in this paper are computed.
.
In the rest of this section we show how the meaning skeletons of
the types of schema considered in this paper are computed.
A number of alternative formalizations for HCs have been proposed
(e.g., [15,,]).
Despite their differences, they share the idea that, in a HC, the
meaning of a node is a specification of the meaning of its father
node. E.g., the meaning of a node labeled with ``clubs'', with a
father node which means ``documents about Ferrari cars'' is
``Ferrari fan clubs''. In DL, this is encoded as
![]() , where
, where
![]() is some node that
connets the meaning of
is some node that
connets the meaning of ![]() with that of
with that of
![]() . If the label of
. If the label of
![]() is for instance ``F40'' (a
Ferrari model) then the meaning of
is for instance ``F40'' (a
Ferrari model) then the meaning of ![]() is ``documents about Ferrari F40 car'', then it is the
meaning of the label of
is ``documents about Ferrari F40 car'', then it is the
meaning of the label of ![]() that acts as modifier of the meaning of
that acts as modifier of the meaning of ![]() . In description logics this is formalized as
. In description logics this is formalized as
![]() . The choice
between the first of the second case essentially depends both on
lexical knowledge, which provides the meaning of the labels, and
domain knowledge, which provides candidate relations between
. The choice
between the first of the second case essentially depends both on
lexical knowledge, which provides the meaning of the labels, and
domain knowledge, which provides candidate relations between
![]() and
and ![]() . The following table summarizes some
meaning skeletons associated with the HC provided above:
. The following table summarizes some
meaning skeletons associated with the HC provided above:
| node | meaning skeleton | |
|---|---|---|
| *[2pt] |
||
| *[3pt] |
|
|
|
|
||
| *[3pt] |
|
|
|
|
||
|
|
||
|
|
Unlike HCs, the formal semantics for ER schemata is widely
shared. In [4],
one can find a comprehensive survey of this area. Roughly
speaking, any ER schema can be converted in an equivalent
set of DL axioms, which express the formal semantics of such a
schema. This formal semantics is defined independently from the
meaning of the single nodes (labels of nodes). Every node is
considered as an atom. To stress this fact in writing meaning
skeletons for ER, we will assign to each node an anonymous
identifier. For instance we use ![]() to denote the 5 nodes of the schema of
Figure 2.
to denote the 5 nodes of the schema of
Figure 2.
If we apply the formal semantics described in [4] to the example of ER given above, we obtain the following meaning skeletons.
| node | label | meaning skeleton |
|---|---|---|
| Publication |
|
|
| Author | ||
|
|
||
|
|
||
| Person | ||
| Article |
|
|
| Journal |
The meaning skeleton of the RDF Schema described in Figure 3 is provided by the formal semantics for RDF schema described for instance in [11]. Most commonly used RDFS constructs can be rephrased in terms of description logics, as discussed in [13]. As we did above, we report the meaning skeletons for some of the nodes of the RDF Schema of Figure 3 in a table, in which we ``anonymize'' the nodes, by giving them meaningless names.
| node | label | meaning skeleton |
|---|---|---|
| Staff | ||
| Researcher | ||
|
|
||
| Paper | ||
| Author | ||
|
|
||
|
|
The observations about ER schemas mostly hold also for the meaning skeletons of RDF Schemas. Moreover, it is worth observing that the comments of the RDF Schema are not considered in the formal semantics, and therefore they are not reported in the meaning skeletons. However, we all know that comments are very useful to understand the real meaning of a concept, especially in large schema. As we will see later, they are indeed very important to select and add the right domain knowledge to the meaning skeleton.
If the label of a node ![]() is
a simple word like ``Image'', or ``Florence'', then
is
a simple word like ``Image'', or ``Florence'', then ![]() represents all
senses that this word can have in any possible context. For
example, WORDNET provides seven
senses for the word ``Images'' and two for ``Florence''. If
represents all
senses that this word can have in any possible context. For
example, WORDNET provides seven
senses for the word ``Images'' and two for ``Florence''. If
![]() and
and ![]() are nodes labeled with these two words, then
are nodes labeled with these two words, then
![]() and
and
![]() .
.
When labels are more complex than a single word, as for
instance ``University of Trento'', or ``Component of
Gastrointestinal Tract'' (occurring in Galen Ontology [16])
then ![]() is a more complex
DL description computable with advanced natural language
techniques. The description of these techniques is beyond the
scope of this paper and we refer the reader to [12]. For the sake of explanation
we therefore concentrate our attention to single word labels.
is a more complex
DL description computable with advanced natural language
techniques. The description of these techniques is beyond the
scope of this paper and we refer the reader to [12]. For the sake of explanation
we therefore concentrate our attention to single word labels.
With respect to our methodology, a body of domain knowledge (called a knowledge base) can be viewed as a set of facts describing the properties and the relations between the objects of a domain. For instance, a geographical knowledge base may contain the fact that Florence is a town located in Italy, and that Florence is also a town located in South Carolina. Clearly, the knowledge base will use two different constants to denote the two Florences. From this simple example, one can see how knowledge base relations are defined between meanings rather than between linguistic entities.
More formally, we define a knowledge base to be a pair
![]() where
where
![]() is a T-box (terminological
box) and
is a T-box (terminological
box) and ![]() is an A-box
(assertional box) of some descriptive language. Moreover, to
address the fact that knowledge is about meanings, we require
that the atomic concepts, roles, and individuals that appear in
the KB be taken from a set of senses provided by one (or more)
linguistic resources. An fragment of knowledge base relevant to
the examples given above is shown in Figure 4.
is an A-box
(assertional box) of some descriptive language. Moreover, to
address the fact that knowledge is about meanings, we require
that the atomic concepts, roles, and individuals that appear in
the KB be taken from a set of senses provided by one (or more)
linguistic resources. An fragment of knowledge base relevant to
the examples given above is shown in Figure 4.
Domain knowledge is used to discover semantic relations
holding between local meanings. Intuitively, given two primitive
concepts ![]() and
and ![]() , we search for a role
, we search for a role
![]() that possibly connect a
that possibly connect a
![]() -object with a
-object with a ![]() -object. As an example,
suppose we need to find a role that connects the concept
-object. As an example,
suppose we need to find a role that connects the concept
![]() and
the nominal concept
and
the nominal concept
![]() ; in the knowledge base of
Figure 4, a candidate relation
is
; in the knowledge base of
Figure 4, a candidate relation
is
![]() .
This is because Florence#1 is a possible value of
the attributed
.
This is because Florence#1 is a possible value of
the attributed
![]() of
an
of
an
![]() .
.
More formally, ![]() is a
semantic relation between the concept
is a
semantic relation between the concept ![]() and
and ![]() w.r.t., the
knowledge base
w.r.t., the
knowledge base ![]() if and
only if
if and
only if
According to this definition one can verify that
![]() is
a semantic relation between
is
a semantic relation between
![]() and
the nominal concept
and
the nominal concept
![]() . Indeed
. Indeed
![]() (condition
(condition ![]() ),
),
![]() (condition
(condition ![]() ) and for no other
primitive concepts
) and for no other
primitive concepts ![]() different
from
different
from
![]() we have that
we have that
![]() (condition
(condition ![]() ). Similarly
). Similarly
![]() is
a semantic relation between the nominal concepts
is
a semantic relation between the nominal concepts
![]() and
and
![]() , but
it is not a semantic relation between
, but
it is not a semantic relation between
![]() and
and
![]() .
.
The relations computed via conditions ![]() -
-![]() can be used also for
disambiguation of local meanings. Namely, the existence of a
semantic relation between two senses of two local meanings,
constitutes an evidence that those senses are the right one. This
allows us to discard all the others. For instance in the
situation depicted in Figure 5, it to keep the
sense
can be used also for
disambiguation of local meanings. Namely, the existence of a
semantic relation between two senses of two local meanings,
constitutes an evidence that those senses are the right one. This
allows us to discard all the others. For instance in the
situation depicted in Figure 5, it to keep the
sense
![]() and
eliminate the other two senses from the local meaning
and
eliminate the other two senses from the local meaning ![]() . Similarly we
prefer
. Similarly we
prefer
![]() on
on
![]() since the former has more semantic relations that the latter.
since the former has more semantic relations that the latter.
As we said in the introduction, the idea and method we proposed can be applied to several fields, including semantic interoperability, information integration, peer-to-peer databases, and so on. Here, as an illustration, we briefly present an application which we developed, where semantic elicitation is used to implement a semantic method for matching hierarchical classifications (HCs).
Matching HCs is an especially interesting case for the Web. Indeed, classifying documents is one of the main techniques people use to improve navigation across large collections of documents. Probably the most blatant example is that of web directories, which most major search engines (e.g. Google, Yahoo!, Looksmart) use to classify web pages and web accessible resources. Suppose that a Web user is navigating Google's directory, and finds an interesting category of documents (for example, the category named 'Baroque' on the left hand side of Figure 6 along the path Arts > Music > History > Baroque) She might want to find semantically related categories in other web directories. One way of achieving this result is by ``comparing'' the meaning of the selected category with the meaning of other categories in different directories. In what follows, we will describe a P2P-like approach to this application, which was developed as part of a tool for supporting distributed knowledge management called KEx [3]. The example discussed in this section is adapted from [6]. The entire matching process is run by CTXMATCH2.
Imagine that both Google and Yahoo had enabled their web
directories with some semantic elicitation system8.
This means that each node in the two web directories is equipped
with a WDL formula which represents its meaning. In addition, we
can imagine that each node contains also a body of domain
knowledge which has been extracted from some ontology; this
knowledge is basically what it is locally known about the content
of the node (for example, given a node labeled ![]() , we can
imagine that it can contain also the information that Tuscany is
a region in Central Italy, whose capital is Florence, and so
on).
, we can
imagine that it can contain also the information that Tuscany is
a region in Central Italy, whose capital is Florence, and so
on).
Let us go back to our Google user interested in Baroque music. When she selects this category, we can imagine that the following process is startedç
In the following table we present some results obtained through CTXMATCH2 for finding relations between the nodes of the portion of Google and Yahoo classifications depicted in Figure 6.
| Google node | Yahoo node | semantic relation |
| Baroque | Baroque | Disjoint ( |
| Visual Arts | Visual Arts | More general than
( |
| Photography | Photography | Equivalent
( |
| Chat and Forum | Chat and Forum | Less general than
( |
In the second example, CTXMATCH2 returns the
`more general than' relation between the nodes Visual
Arts. This is a rather sophisticated result: indeed, world
knowledge provides the information that `photography ![]() visual art' (
visual art' (
![]() ).
From structural knowledge, we can deduce that, while in the left
structure the node Visual Arts denotes the whole concept
(in fact photography is one of its children), in the
right structure the node Visual Arts denotes the concept
`visual arts except photography' (in fact photography is
one of its siblings). Given this information, it easy to deduce
that, although despite the two nodes lie on the same path, they
have different meanings.
).
From structural knowledge, we can deduce that, while in the left
structure the node Visual Arts denotes the whole concept
(in fact photography is one of its children), in the
right structure the node Visual Arts denotes the concept
`visual arts except photography' (in fact photography is
one of its siblings). Given this information, it easy to deduce
that, although despite the two nodes lie on the same path, they
have different meanings.
The third example shows how the correct relation holding
between nodes Photography is returned (`equivalence'),
despite the presence of different paths, as world knowledge tells
us that
![]() .
.
Finally, between the nodes Chat and Forum a `less general than' relation is found as world knowledge gives us the axiom `literature is a humanities'.
This work has been inspired from the approach described in [12] in which the technique of semantic elicitation has been applied to the special case of hierarchical classification. The approach described in this paper extends this initial approach in three main directions. First, the logic in which the meaning is expressed in some description logic, while in [12] meaning was encoded in propositional logic. Second, [12] adopts only WordNet as both linguistic and domain knowledge repository, while in this approach we allow the use of multiple linguistic resources, and knowledge bases. Third, in [12] no particular attention was paid to structural knowledge, while here we introduced the concept of a meaning skeleton, which captures exactly this notion.
The paper [1] describes an approach which enrich xml schema with the semantic encoded in an ontology. This approach is similar in the spirit of the idea of semantic elicitation of schemas, but it does not make an extensive use of explicit structural knowledge, and of linguistic knowledge, which are two of the three knowledge sources used in our approach.
The approach described in [18] describes a possible application of the linguistic enrichment of an ontology in the area of keyword based document retrieval. This approach is quite similar in the spirit on what we have proposed here, with the limitation of considering only hierarchical classifications. Moreover, in the process of enriching a concept hierarchy, no domain knowledge is used.
Finally, most of the approaches of schema matching uses linguistic knowledge (WordNet) and domain knowledge to find correspondences between elements of heterogeneous schemata. Among all the approaches CTXMATCH [5] and [10] is based on the idea of matching meaning, rather than matching syntax. Both approaches implement a two step algorithm, and the first phase computes the meaning of a node by using linguistic and domain knowledge. However both approaches are based on propositional logic.
Semantic elicitation mat be an important method for bootstrapping semantics on the web. Our method does not address the issue of extracting knowledge from documents, which of course will be the main source of semantic information. But knowledge extraction from documents is still an expensive and error prone task, as it must address a lot of well-known problems related to natural language analysis. Instead, semantic elicitation can be applied to objects which have a simpler structure (labels are typically quite simple from a linguistic point of view), and thus is less demanding from a computational point of view and more precise (needless to say, a lot of errors may occur, see [5] for a few tests). But schemas, as we said, are very common on the web, and have a very high informative power. Moreover, in many applications in the area integration of semantic web services the only available information is based on schemas and no data are present. Therefore, we assume that, in the short-mid term, this would be one of the main ways to add semantics to data on the web on a large scale.