WWW 2006, May 23-26, 2006, Edinburgh, Scotland. 2006 1-59593-332-9/06/0005

Using Symbolic Objects to Cluster Web Documents

Esteban Meneses

Costa Rica Institute of Technology
Computing Research Center
Cartago, Costa Rica

Oldemar Rodríguez-Rojas

University of Costa Rica
School of Mathematics
San José, Costa Rica

Copyright is held by the author/owner(s).
WWW 2006, May 23-26, 2006, Edinburgh, Scotland.
ACM 1-59593-323-9/06/0005.

ABSTRACT

Web Clustering is useful for several activities in the WWW, from automatically building web directories to improve retrieval performance. Nevertheless, due to the huge size of the web, a linear mechanism must be employed to cluster web documents. The k-means is one classic algorithm used in this problem. We present a variant of the vector model to be used with the k-means algorithm. Our representation uses symbolic objects for clustering web documents. Some experiments were done with positive results and future work is optimistic.

Categories & Subject Descriptors

I.7.mDocument and Text Processing
Miscellaneous D.2.8Software EngineeringMetrics[performance measures]

General Terms

Algorithms

Keywords

Symbolic Data Analysis, Web Clustering

1 Introduction

The aim of web clustering is to group web documents into very identifiable classes in such a way that common web activities can be improved. However, due to the huge quantity of web documents, techniques focused on web clustering must be efficient enough to manipulate even millions of elements. Because of that, linear models are generally preferred. One such linear model is the k-means algorithm [4], which can iteratively cluster a document collection into $k$ classes.

The traditional k-means algorithm uses the vector model [2] for representing documents. In this model, given a web document collection $\mathcal{D}$ with $n$ documents, every element $d \in \mathcal{D}$ is represented by a vector $x_d$ in a $m$-dimensional space, typically $\mathcal{R}^m$. Each dimension stands for the frequency of term $t_i$ in the document $d$, where $i=1,2,...,m$. A dictionary with the $m$ terms $\{t_1,t_2,...,t_m\}$ can be build with the $m$ more frequent terms in the collection $\mathcal{D}$ [6], for example.

The k-means algorithm works by finding $k$ centers of gravity $\{g_1,g_2,...,g_k\}$, each of which will attract some elements and form a cluster. The center $g_i$ represents cluster $C_i$. Initially, these $k$ centers are randomly selected. Then, iteratively the elements of $\mathcal{D}$ will be assigned to some cluster. In each phase every element is associated with the nearest center according to some $distance$ measure $\lambda$. After that, centers are recalculated to minimize the criteria:

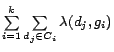
$\sum\limits_{i=1}^{k}\sum\limits_{d_j \in C_i}\lambda(d_j,g_i)$

There are many distance measures in the literature [7], but Jaccard Extended Distance has showed good clustering performance [6]. This function was used in this work.

This poster presents a variant for the representation of web documents using symbolic objects. The details of some experiments are first showed. Conclusions and future work are left for the final part.

2 Symbolic Web Clustering

We extended the standard k-means algorithm using symbolic objects [1] instead of real-valued vectors for representing web documents. Symbolic objects are better at representing concepts rather than individuals. Its strength resides in its capacity for storing the variablility of concepts. In this case, the web page in considered as a concept that is formed by sections of the HTML code.

Symbolic objects are vectors where each entry can have any type: scalar, set, interval, histogram, graph, you name it. In the particular case of this poster, the histogram representation was explored.

Each document is represented with a symbolic object with four histogram entries. These four variables correspond to frequency of terms in four sections of the HTML code: text, bold, links and title. Each symbolic object is built after the web collection is analyzed and the most frequent terms are obtained. Previously, $stopwords$ are eliminated and Porter's stemming algorithm is applied to every word in any of those four sections.

More formally, each document $d$ in the collection $\mathcal{D}$ is represented by the symbolic object $x_d$ in $m$ histogram dimensions $\{x_{d1},x_{d2},...,x_{dm}\}$. Each variable $x_{di}$ is a normalized histogram $\{x_{di1},x_{di2},...,x_{dip}\}$ with $p$ $categories$ or $modalities$.

The distance measure used is based on the affinity index [1] and uses weights $w_i$ for every dimension:

$\lambda(x_d,x_{d'}) = 1 - \sum\limits_{i=1}^{m}w_i\sum\limits_{j=1}^{p}\sqrt{x_{dij}*x_{d'ij}}$

3 Results


Table 1: k-means results
Model Rand Index Mutual Info. Time
Vector 0.7374 0.1559 2.56 s
Histogram-10 0.7401 0.1571 0.28 s
Histogram-30 0.7416 0.1614 0.78 s
Histogram-50 0.7417 0.1615 1.48 s


Table 2: Global k-means results
Model Rand Index Mutual Info. Time
Vector 0.7312 0.1546 3519 s
Histogram-10 0.7397 0.1556 320 s
Histogram-30 0.7433 0.1670 1062 s
Histogram-50 0.7399 0.1613 1714 s

We used a subset of the web collection from [3] for testing our approach. This series contains 684 documents from 4 classes. The evaluation of the resulting clusters was made using the rand index and the mutual information measures [7]. The former computes how similar is the clustering obtained to the manual clustering (also present in the web collection). The latter calculates the quality of the clusters according to how compact the cluster is. Experiments were repeated 50 times each over database.

The results for web collection clustering are presented in Table 1. The vectorial representation of this series is formed by a 684 x 200 matrix. On the other hand, each symbolic model is accompanied by the number of categories in the histogram, i.e. $p$. Every symbolic representation appears to be slightly better than the vector representation in both indexes. Using 30 categories is a good balance between accuracy and efficiency. Adding more categories to the histograms doesn't improve much more the clustering.

It can be seen in table 1 the average time taken by the different approaches to cluster this series. The symbolic objects show how efficient such representation can be. Using 10 categories in histograms, symbolic objects are near 9 times faster than vector representation.

Table 2 shows the results for this series using an approach called global k-means [5]. This clustering method is completely deterministic and is based on the computation of good initial clusters. This algorithm iteratively builds the best clustering for web collection, using 1 cluster the first time, 2 clusters the second time, until $k$ clusters are considered. However, each time it passes throughout all individuals, making global k-means computationally costly. In table 2 it can be appreciated that the best results were obtained by the 30 categories histogram representation, which is again three times faster than the vectorial model.

Figure 1 shows two PCA or principal component analysis [1] over this series. The PCA is a dimension reduction technique. The left graphic was made using the classic representation, while the right graphic was made with symbolic representation. The inertia percentage (how much information is conserved after the transformation) of the classic PCA was 28.89%, but using symbolic PCA the inertia percentage is 62.90%. The graphic on the right doesn't show points, as in the left, but rectangles that represent the variability of concepts.

Besides these results, we also used the quality measures from [8]. The quality of the partition can be decomposed for each variable, to measure the importance of each variable to form the clustering. In one run of this series, using a symbolic object of histograms with 30 categories, the quality indexes for the different variables were: text=0.0348, link=0.0211, bold=0.0215 and title=0.0573. Meaning this that the title in web documents helps a lot in building the clustering.

Figure 1: PCA for web collection
\begin{figure} \centering \epsfig{file=pca.eps, height=1.4in, width=3.4in} \end{figure}

4 Conclusions and Future Work

Symbolic objects can address the problem of web clustering with efficiency and semantic power. Given a symbolic object, it is more clear for the user what information is contained into it. In the web document clustering problem, symbolic models can be more accurate and even more efficient than vectorial representations.

We are currently working on different distance measures between histograms and a variant of k-means algorithm to take into account what is called strong forms to better clustering a document collection.

In the future, we would like to extend the representation of the symbolic object used in this poster to include more information about the document.

Bibliography

1
H.-H. Bock and E. Diday.
Analysis of Symbolic Data.
Springer-Verlag, 2000.
2
S. Chakrabarti.
Mining the Web.
Morgan Kaufmann Publishers, 2003.
3
D. Crabtree, X. Gao, and P. Andreae.
Improving web clustering by cluster selection.
International Conference on Web Intelligence, 2005.
4
R. Duda and P. Hart.
Pattern Classification and Scene Analysis.
New York: Wiley, 1973.
5
A. Likas, N. Vlassis, and J. J. Verbeek.
The global k-means algorithm.
Pattern Recognition, 36(1), 2003.
6
A. Schenker, M. Last, H. Bunke, and A. Kandel.
A comparison of two novel algorithms for clustering web documents.
2nd IWWDA, 2003.
7
A. Strehl, J. Ghosh, and R. Mooney.
Impact of similarity measures on web-page clustering.
AAAI-2000: Workshop of Artificial Intelligence for Web Search, 2000.
8
R. Verde, Y. Lechevallier, and M. Chavent.
Symbolic clustering interpretation and visualization.
Journal of Symbolic Data Analysis, 1(1), 2003.