Compressing and Searching XML Data Via Two Zips

Paolo Ferragina

Dipartimento di Informatica
Università di Pisa, Italy

Fabrizio Luccio

Dipartimento di Informatica
Università di Pisa, Italy

Giovanni Manzini

Dipartimento di Informatica
Università del Piemonte Orientale, Italy

S. Muthukrishnan

Department of Computer Science
Rutgers University, USA

Copyright is held by the World Wide Web Conference Committee (IW3C2). Distribution of these papers is limited to classroom use, and personal use by others.
WWW 2006, May 23.26, 2006, Edinburgh, Scotland.
ACM 1-59593-323-9/06/0005.

ABSTRACT

XML is fast becoming the standard format to store, exchange and publish over the web, and is getting embedded in applications. Two challenges in handling XML are its size (the XML representation of a document is significantly larger than its native state) and the complexity of its search (XML search involves path and content searches on labeled tree structures). We address the basic problems of compression, navigation and searching of XML documents. In particular, we adopt recently proposed theoretical algorithms [11] for succinct tree representations to design and implement a compressed index for XML, called XBZIPINDEX, in which the XML document is maintained in a highly compressed format, and both navigation and searching can be done uncompressing only a tiny fraction of the data. This solution relies on compressing and indexing two arrays derived from the XML data. With detailed experiments we compare this with other compressed XML indexing and searching engines to show that XBZIPINDEX has compression ratio up to 35% better than the ones achievable by those other tools, and its time performance on some path and content search operations is order of magnitudes faster: few milliseconds over hundreds of MBs of XML files versus tens of seconds, on standard XML data sources.

Categories & Subject Descriptors

E.1 Data Structures: Arrays, Tables; E.4 Coding and Information Theory: Data compaction and compression; H.3 Information Storage and Retrieval :Content Analysis and Indexing, Information Storage, Information Search and Retrieval.

General Terms

Algorithms, Experimentation.

Keywords

Labeled trees, XML compression and indexing.

1 Introduction

In 1996 the W3C started to work on XML as a way to enable data interoperability over the internet; today, XML is the standard for information representation, exchange and publishing over the Web. In 2003 about 3% of global network traffic was encoded in XML; this is expected to rise to 24% by 2006, and to at least 40% by 2008 [15]. XML is also seeping into many applications [1].

XML is popular because it encodes a considerable amount of metadata in its plain-text format; as a result, applications can be more savvy about the semantics of the items in the data source. This comes at a cost. At the core, the challenge in XML processing is three-fold. First, XML documents have a natural tree-structure, and many of the basic tasks that are quite easy on arrays and lists--such as indexing, searching and navigation--become more involved. Second, by design, XML documents are wordy since they nearly repeat the entire schema description for each data item. Therefore, data collections become more massive in their XML representations, and present problems of scale. As a result, XML can be ``inefficient and can burden a company's network, processor, and storage infrastructures'' [15]. Finally, XML documents have mixed elements with both text and numerical or categorical attributes. As a result, XML queries are richer than commonly used SQL queries; they, for example, include path queries on the tree structure and substring queries on contents.

In this paper we address these basic challenges. In particular, we address the problems of how to compress XML data, how to provide access to its contents, how to navigate up and down the XML tree structure (cfr. DOM tree), and how to search for simple path expressions and substrings. The crux is, we focus on doing all of these tasks while keeping the data still in its compressed form and uncompressing only a tiny fraction of the data for each operation.

Problems and the Background. As the relationships between elements in an XML document are defined by nested structures, XML documents are often modeled as trees whose nodes are labeled with strings of arbitrary length drawn from a usually large alphabet $\Sigma$. These strings are called tag or attribute names for the internal nodes, and content data for the leaves (shortly PCDATA). See Fig. 1 for an example. Managing XML documents (cfr. their DOM tree) therefore needs efficient support of navigation and path expression search operations over their tree structure. With navigation operations we mean:

With path expressions, we mean two basic search operations that involve structure and content of the XML document tree:

The first search operation, called SubPathSearch, corresponds to an XPATH query having the form /$\Pi $, where $\Pi $ is a fully-specified path consisting of tag/attribute names. The second search operation, called ContentSearch, corresponds to an XPATH query of the form /$\Pi $[contains(.,$\gamma $)], where $\Pi $ is a fully-specified path and $\gamma $ is an arbitrary string of characters.

The text book solution to represent the XML document tree for navigation--finding parents and children of nodes in the tree--uses a mixture of pointers and hash arrays. Unfortunately, this representation is space consuming and practical only for small XML documents. Furthermore, while tree navigation takes constant time per operation, SubPathSearch and ContentSearch need the whole scan of the document tree which is expensive. In theory, there are certain sophisticated solutions (see [5, 14] and references therein) for tree navigation in succinct space but they do not support the search operations above. If SubPathSearch is a key concern, we may use any summary index data structure [6] that represents all paths of the tree document in an index (two famous examples are Dataguide [16] and $1$- or $2$-indexes [22]). This significantly increases the space needed by the index, and yet, it does not support ContentSearch queries efficiently. If ContentSearch queries are the prime concern, we need to resort more sophisticated approaches-- like XML-native search engines, e.g. XQUEC [4], F&B-INDEX [29], etc.; all of these engines need space several times the size of the XML representation.

At the other extreme, XML-conscious compressors such as [21,3,8]--do compress XML data into small space, but any navigation or search operation needs the decompression of the entire file. Even XML-queryable compressors like [27,23,10], that support more efficient path search operations, incur into the scan of the whole compressed XML file and need the decompression of large parts of it in the worst case. This is expensive at query time.

Recently, there has been some progress in resolving the dichotomy of time-efficient vs space-efficient solutions [11]. The contribution in [11] is the XBW transform that represents a labeled tree using two arrays: the first contains the tree labels arranged in an appropriate order, while the second is a binary array encoding the structure of the tree. The XBW transform can be computed and inverted in (optimal) linear time with respect to the number of tree nodes, and is as succinct as the information contained in the tree would allow. Also, [11] shows that navigation and search operations over the labeled tree can be implemented over the XBW transform by means of two standard query operations on arrays: rank $_{\alpha}(A,k)$ computes the number of occurrences of a symbol $\alpha$ in the array prefix $A[1,k]$; select $_{\alpha}(A,h)$ computes the position in $A$ of the $h$th occurrence of $\alpha$. Since the algorithmic literature offers several efficient solutions for rank and select queries (see [5,17] and references therein), the XBW transform is a powerful tool for compressing and searching labeled trees.


Our Contribution. The result in [11] is theoretical and relies on a number of sophisticated data structures for supporting rank and select queries. In this paper, we show how to adapt XBW transform to derive a compressed searching tool for XML, and present a detailed experimental study comparing our tools with existing ones. More precisely, our contribution is as follows.


(1) We present an implementation of the XBW transform as a compressor (hereafter called XBZIP). This is an attractively simple compressor, that relies on standard compression methods to handle the two arrays in the XBW transform. Our experimental studies show that this is comparable in its compression ratio to the state-of-the-art XML-conscious compressors (which tend to be significantly more sophisticated in employing a number of heuristics to mine some structure from the document in order to compress ``similar contexts''). In contrast, the XBW transform automatically groups contexts together by a simple sorting step involved in constructing the two arrays. In addition, XBZIP is a principled method with provably near-optimal compression [11].


(2) We present an implementation of the XBW transform as a compressed index (hereafter called XBZIPINDEX). This supports navigation and search queries very fast uncompressing only a tiny fraction of the document. Compared to similar tools like XGRIND [27], XPRESS [23] and XQZIP [10], the compression ratio of XBZIPINDEX is up to 35% better, and its time performance on SubPathSearch and ContentSearch search operations is order of magnitudes faster: few milliseconds over hundreds of MBs of XML files versus tens of seconds (because of the scan of the compressed data inherent in these comparable tools). The implementation of XBZIPINDEX is more challenging since in addition to the XBW transform, like in [11], we need data structures to support rank and select operations over the two arrays forming XBW. Departing from [11] which uses sophisticated methods for supporting these operations on compressed arrays, we introduce the new approach of treating the arrays as strings and employing a state-of-the-art string indexing tool (the FM-index [13]) to support structure+content search operations over the document tree. This new approach of XBZIPINDEX has many benefits since string indexing is a well-understood area; in addition, we retain the benefits of [11] in being principled, with concrete performance bounds on the compression ratio as well as time to support navigation and search operations.


Both the set of results above are obtained by suitably modifying the original definition of XBW given in [11] that works for labeled trees to better exploit the features of XML documents. The final result is a library of XML compression and indexing functions, consisting of about 4000 lines of C code and running under Linux and Windows. The library can be either included in another software, or it can be directly used at the command-line with a full set of options for compressing, indexing and searching XML documents.

XBZIPINDEX has additional features and may find other applications besides compressed searching. For example, it supports tree navigation (forward and backward) in constant time, allows the random access of the tree structure in constant time, and can explore or traverse any subtree in time proportional to their size. This could be used within an XML visualizer or within native-XML search engines such as XQUEC [4] and F&B-INDEX [29]. There are more general XML queries like twig or XPath or XQuery; XBZIPINDEX can be used as a core to improve the performance of known solutions. Another such example is that of structural joins which are key in optimizing XML queries. Previous work involving summary indexes [7,19], or node-numbering such as VIST [28] or PRUFER [25] might be improved using XBZIPINDEX.

2 Compact representation of DOM trees

Figure 1: An XML document $d$ (left) and its corresponding ordered labeled tree ${\cal T}$ (right). 

<biblio>
  <book id=1>
    <author>J. Austin</author>
    <title>Emma</title>
  </book>
  <book id=2>
    <author>C. Bronte</author>
    <title>Jane Eyre</title>
  </article>
</biblio>
\includegraphics[width=7cm]{jane4.eps}

Given an arbitrary XML document $d$, we now show how to build an ordered labeled tree ${\cal T}$ which is equivalent to the DOM representation of $d$. Tree ${\cal T}$ consists of four types of nodes defined as follows:

  1. Each occurrence of an opening tag <t> originates a tag node labeled with the string <t.
  2. Each occurrence of an attribute name a originates an attribute node labeled with the string @a.
  3. Each occurrence of an attribute value or textual content of a tag, say $\rho$, originates two nodes: a text-skip node labeled with the character =, and a content node labeled with the string $\mbox{$\emptyset$}\rho$, where $\mbox{$\emptyset$}$ is a special character not occurring elsewhere in $d$.

The structure of the tree ${\cal T}$ is defined as follows (see Figure 1). An XML well-formed substring of $d$, say $\sigma =$ <t a$_1$="$\rho_1$" $\ldots$ a$_k$="$\rho_1$"> $\tau$ </t>, generates a subtree of ${\cal T}$ rooted at a node labeled <t. This node has $k$ children (subtrees) originating from $t$'s attribute names and values (i.e. @a $_i \rightarrow {\tt =} \rightarrow \rho_i$), plus other children (subtrees) originating by the recursive parsing of the string $\tau$. Note that attribute nodes and text-skip nodes have only one child. Tag nodes may have an arbitrary number of children. Content nodes have no children and thus form the leaves of ${\cal T}$.1

1 The XBW Transform

We show how to compactly represent the tree ${\cal T}$ by adapting the XBW transform introduced in [11]. The XBW transform uses path-sorting and grouping to linearize the labeled tree ${\cal T}$ into two arrays. As shown in [11], this ``linearized'' representation is usually highly compressible and efficiently supports navigation and search operations over ${\cal T}$. Note that we can easily distinguish between internal-node labels vs leaf labels because the former are prefixed by either <, or @, or =, whereas the latter are prefixed by the special symbol $\emptyset$.

Let $n$ denote the number of internal nodes of ${\cal T}$ and let $\ell$ denote the number of its leaves, so that the total size of ${\cal T}$ is $t=n+\ell$ nodes. For each node $u\in{\cal T}$, let $\alpha[u]$ denote the label of $u$, $\mbox{\sf last}[u]$ be a binary flag set to $1$ if and only if $u$ is the last (rightmost) child of its parent in ${\cal T}$, and $\pi[u]$ denote the string obtained by concatenating the labels on the upward path from $u$'s parent to the root of ${\cal T}$.

To compute the XBW transform we build a sorted multi-set ${\cal S}$ consisting of $t$ triplets, one for each tree node (see Fig. 2). Hereafter we will use ${\cal S}_{\sf last}[i]$ (resp. ${\cal S}_\alpha [i]$, ${\cal S}_\pi [i]$) to refer to the $\mbox{\sf last}$ (resp. $\alpha$, $\pi$) component of the $i$-th triplet of ${\cal S}$. To build ${\cal S}$ and compute the XBW transform we proceed as follows:


  1. Visit ${\cal T}$ in pre-order; for each visited node $u$ insert the triplet $s[u] = \langle \mbox{\sf last}[u], \alpha[u], \pi[u] \rangle$ in ${\cal S}$;
  2. Stably sort ${\cal S}$ according to the $\pi$-component of its triplets;
  3. Form $\mbox{{\sf XBW}}(d) = \langle\widehat{{\cal S}}_{{\sf last}}, \widehat{{\cal S}}_\alpha , \widehat{{\cal S}}_{{\sf pcdata}}\rangle$ , where $\widehat{{\cal S}}_{{\sf last}}= {\cal S}_{\sf last}[1,n]$ , $\widehat{{\cal S}}_\alpha = {\cal S}_\alpha [1,n]$, and $\widehat{{\cal S}}_{{\sf pcdata}}= {\cal S}_\alpha [n+1,t]$ .

Since sibling nodes may be labeled with the same symbol, several nodes in ${\cal T}$ may have the same $\pi$-component (see Fig. 1). The stability of sorting at Step 2 is thus needed to preserve the identity of triplets after the sorting. The sorted set ${\cal S}[1,t]$ has the following properties: $(i)$ ${\cal S}_{\sf last}$ has $n$ bits set to 1 (one for each internal node), the other $t-n$ bits are set to 0; $(ii)$ ${\cal S}_\alpha $ contains all the labels of the nodes of ${\cal T}$; $(iii)$ ${\cal S}_\pi $ contains all the upward labeled paths of ${\cal T}$ (and it will not be stored). Each path is repeated a number of times equal to the number of its offsprings. Thus, ${\cal S}_\alpha $ is a lossless linearization of the labels of ${\cal T}$, whereas ${\cal S}_{\sf last}$ provides information on the grouping of the children of ${\cal T}$'s nodes.

Figure 2: The set ${\cal S}$ after the pre-order visit of ${\cal T}$ (left). The set ${\cal S}$ after the stable sort (right). The three arrays $\widehat{{\cal S}}_{{\sf last}}, \widehat{{\cal S}}_\alpha , \widehat{{\cal S}}_{{\sf pcdata}}$ , output of the XBW transform (bottom).

${\cal S}_{\sf last}$ ${\cal S}_\alpha $ ${\cal S}_\pi $
1 <biblio empty string
0 <book <biblio
0 @id <book<biblio
1 = @id<book<biblio
1 $\emptyset$1 =@id<book<biblio
0 <author <book<biblio
1 = <author<book<biblio
1 $\emptyset$J. Austin =<author<book<biblio
1 <title <book<biblio
1 = <title<book<biblio
1 $\emptyset$Emma =<title<book<biblio
1 <book <biblio
0 @id <book<biblio
1 = @id<book<biblio
1 $\emptyset$2 =@id<book<biblio
0 <author <book<biblio
1 = <author<book<biblio
1 $\emptyset$C. Bronte =<author<book<biblio
1 <title <book<biblio
1 = <title<book<biblio
1 $\emptyset$Jane Eyre =<title<book<biblio
\begin{picture}(50,0) % thicklines \put(0,7){{\small Stable sort}} \put(0,0){\vector(1,0){50}} \end{picture}
Rk ${\cal S}_{\sf last}$ ${\cal S}_\alpha $ ${\cal S}_\pi $
1 1 <biblio empty string
2 1 = <author<book<biblio
3 1 = <author<book<biblio
4 0 <book <biblio
5 1 <book <biblio
6 0 @id <book<biblio
7 0 <author <book<biblio
8 1 <title <book<biblio
9 0 @id <book<biblio
10 0 <author <book<biblio
11 1 <title <book<biblio
12 1 = <title<book<biblio
13 1 = <title<book<biblio
14 1 = @id<book<biblio
15 1 = @id<book<biblio
16 1 $\emptyset$J. Austin =<author<book<biblio
17 1 $\emptyset$C. Bronte =<author<book<biblio
18 1 $\emptyset$Emma =<title<book<biblio
19 1 $\emptyset$Jane Eyre =<title<book<biblio
20 1 $\emptyset$1 =@id<book<biblio
21 1 $\emptyset$2 =@id<book<biblio
\fbox{\begin{minipage}{12cm} \vspace{-\abovedisplayskip} \begin{eqnarray*} \wide... ...}Jane Eyre\mbox{$\emptyset$}1\mbox{$\emptyset$}2} \end{eqnarray*}\end{minipage}}

We notice that the XBW transform defined in Step 3 is slightly different from the one introduced in [11] where XBW is defined as the pair $\langle{\cal S}_{\sf last},{\cal S}_\alpha \rangle$. The reason is that here the tree ${\cal T}$ is not arbitrary but derives from an XML document $d$. Indeed we have that ${\cal S}_\alpha [1,n]$ contains the labels of the internal nodes, whereas ${\cal S}_\alpha [n+1,t]$ contains the labels of the leaves, that is, the PCDATA. This is because if $u$ is a leaf the first character of its upward path $\pi[u]$ is = which we assume is lexicographically larger than the characters < and @ that prefix the upward path of internal nodes (see again Fig. 2). Since leaves have no children, we have that ${\cal S}_{\sf last}[i]=1$ for $i=n+1,\ldots,t$. Avoiding the wasteful representation of ${\cal S}_{\sf last}[n+1,t]$ is the reason for which in Step 3 we split ${\cal S}_\alpha $ and ${\cal S}_{\sf last}$ into $\langle\widehat{{\cal S}}_{{\sf last}}, \widehat{{\cal S}}_\alpha , \widehat{{\cal S}}_{{\sf pcdata}}\rangle$ .

In [11] the authors describe a linear time algorithm for retrieving ${\cal T}$ given $\langle{\cal S}_{\sf last},{\cal S}_\alpha \rangle$. Since it is trivial to get the document $d$ from $\mbox{{\sf XBW}}(d)$ we have that $\mbox{{\sf XBW}}(d)$ is a lossless encoding of the document $d$. It is easy to prove that $\mbox{{\sf XBW}}(d)$ takes at most $(17/8)n + \ell$ bytes in excess to the document length (details in the full version). However, this is an unlikely worst-case scenario since many characters of $d$ are implicitly encoded in the tree structure (i.e., spaces between the attribute names and values, closing tags, etc). In our experiments $\mbox{{\sf XBW}}(d)$ was usually about 90% the original document size. Moreover, the arrays $\widehat{{\cal S}}_{{\sf last}}$, $\widehat{{\cal S}}_\alpha $, and $\widehat{{\cal S}}_{{\sf pcdata}}$ are only an intermediate representation since we will work with a compressed image of these three arrays (see below).

Finally, we point out that it is possible to build the tree ${\cal T}$ without the text-skip nodes (the nodes with label =). However, if we omit these nodes PCDATA will appear in ${\cal S}_\alpha $ intermixed with the labels of internal nodes. Separating the tree structure (i.e. $\langle\widehat{{\cal S}}_{{\sf last}}, \widehat{{\cal S}}_\alpha \rangle$ ) from the textual content of the document (i.e. $\widehat{{\cal S}}_{{\sf pcdata}}$) has a twofold advantage: $(i)$ the two strings $\widehat{{\cal S}}_\alpha $ and $\widehat{{\cal S}}_{{\sf pcdata}}$ are strongly homogeneous hence highly compressible (see Sect. 2.2), $(ii)$ search and navigation operations over ${\cal T}$ are greatly simplified (see Sect. 2.3).


2 Why XBW$(d)$ compresses well

Suppose the XML fragment of Fig. 1 is a part of a large bibliographic database for which we have computed the XBW transform. Consider the string =<author. The properties of the XBW transform ensure that the labels of the nodes whose upward path is prefixed by =<author are consecutive in ${\cal S}_\alpha $. In other words, there is a substring of ${\cal S}_\alpha $ consisting of all the data (immediately) enclosed in an <author> tag. Similarly, another section of ${\cal S}_\alpha $ contains the labels of all nodes whose upward path is prefixed by, say, =@id<book and will therefore likely consists of id numbers. This means that ${\cal S}_\alpha $, and therefore $\widehat{{\cal S}}_\alpha $ and $\widehat{{\cal S}}_{{\sf pcdata}}$, will likely have a strong local homogeneity property.2

We point out that most XML-conscious compressors are designed to ``compress together'' the data enclosed in the same tag since such data usually have similar statistics. The above discussion shows that the XBW transform provides a simple mechanism to take advantage of this kind of regularity. In addition, XML compressors (e.g. XMILL, SCMPPM, XMLPPM) usually look at only the immediately enclosing tag since it would be too space consuming to maintain separate statistics for each possible group of enclosing tags. Using the XBW transform we can overcome this difficulty since the different groups of enclosing tags are considered sequentially rather than simultaneously. For example, for a bibliographic database, ${\cal S}_\alpha $ would contain first the labels of nodes with upward path =<author<article, then the labels with upward path =<author<book, and finally the labels with upward path =<author<manuscript, and so on. Hence, we can either compress all the author names together, or we can decide to compress the three groups of author names separately, or adopt any other optimization scheme.


3 Navigation and search using XBW$(d)$

Recall that every node of ${\cal T}$ corresponds to an entry in the sorted multiset ${\cal S}$ (see Fig. 2). We (logically) assign to each tree node a positive integer equal to its rank in ${\cal S}$. This number helps in navigation and search because of the following two properties of the sorted multiset ${\cal S}$.


  1. Let $u_1, \ldots, u_c$ be the children of a node $u$ in ${\cal T}$. The triplets $s[u_1], \ldots, s[u_c]$ lie contiguously in ${\cal S}$ following this order. Moreover, the last triplet $s[u_c]$ has its $\mbox{\sf last}$-component set to 1, whereas all the other triplets have their $\mbox{\sf last}$-component set to 0.
  2. Let $v_1, v_2$ denote two nodes with the same label (i.e., $\alpha[v_1] = \alpha[v_2]$). If $s[v_1]$ precedes $s[v_2]$ in ${\cal S}$, then the children of $v_1$ precede the children of $v_2$ in ${\cal S}$.

For every internal node label $\beta$, we define ${\sf F}(\beta)$ as the rank of the first row of ${\cal S}$ such that ${\cal S}_\pi $ is prefixed by $\beta$. Thus, for the example of Fig. 2 we have ${\sf F}(\mbox{\sf$<$author})=2$, ${\sf F}(\mbox{\sf$<$biblio})=4$, ${\sf F}(\mbox{\sf$<$book})=6$, and so on. Suppose that the tree contains $m$ internal nodes with label $\beta$. We can rephrase Properties 1-2 above stating that starting from position ${\sf F}(\beta)$ there are $m$ groups of siblings which are the offsprings of the nodes with label $\beta$. The end of each group is marked by a value 1 in the array ${\cal S}_{\sf last}$, and the $k$-th group of siblings gives the children of the node corresponding to the $k$-th occurrence of the label $\beta$ in ${\cal S}_\alpha $.

To efficiently navigate and search ${\cal T}$, in addition to $\mbox{{\sf XBW}}(d)$ and the array ${\sf F}$, we need auxiliary data structures for the rank and select operations over the arrays $\widehat{{\cal S}}_{{\sf last}}$ and $\widehat{{\cal S}}_\alpha $. Recall that given an array $A[1,n]$ and a symbol $c$, $\mbox{{\sf rank}}_c(A,i)$ denotes the number of times the symbol $c$ appears in $A[1,i]$, and $\mbox{{\sf select}}_c(A,k)$ denotes the position in $A$ of the $k$-th occurrence of the symbol $c$.

The pseudocode of the procedure for computing the rank of the children of the node with rank $i$ is shown in Fig. 3 to highlight its simplicity. We first compute the label $c$ of node $i$ by setting $c=\widehat{{\cal S}}_\alpha [i]$ (Step 1). Then, we set $k=\mbox{{\sf rank}}_c(\widehat{{\cal S}}_\alpha ,i)$ (Step 2) and we have that ${\cal S}[i]$ is the $k$-th node with label $c$ is $\widehat{{\cal S}}_\alpha $. Because of properties 1-2 the children of ${\cal S}[i]$ are the $k$-th group of siblings starting from position $y={\sf F}(c)$. The rank of the children is therefore easily computed by way of rank/select operations over the array $\widehat{{\cal S}}_{{\sf last}}$ (Steps 4-6). For example, in Fig. 2 for $i=5$ we have $c=\mbox{\sf$<$book}$ and $k=2$ so we are interested in the second group of siblings starting from ${\sf F}(\mbox{\sf$<$book})=6$.

The procedures for navigation and SubPathSearch have a similar simple structure and are straightforward adaptations of similar procedures introduced in [11].The only nontrivial operations are the rank and select queries mentioned above. Note that navigation operations require a constant number of rank/select queries, and the SubPathSearch procedure requires a number of rank/select queries proportional to the length of the searched path. In this paper we introduce the new procedure ContentSearch that combines the techniques of [11] with the FM-index data structure of [12,13] and will be discussed in Sect. 3.3.

Figure 3: Algorithm for computing the range $(\mbox{\sf First},\mbox{\sf Last})$ such that ${\cal S}[\mbox{\sf First}], {\cal S}[\mbox{\sf First}+1],\ldots,{\cal S}[\mbox{\sf Last}]$ are the children of node ${\cal S}[i]$.

\begin{figure}\hrule {\itemsep=-2pt\baselineskip=12pt\smallskip {Algorithm {\sf ... ...}, \mbox{\sf Last})$.\end{enumerate} \vspace*{-2pt}\vskip0pt}\hrule \end{figure}


3 Implementation


1 Computation of the XBW transform

To build the tree ${\cal T}$ we parse the input document $d$ using the Expat library by James Clark.3 Expat is a stream oriented parser written in C. We set its handlers in order to create the tree nodes and their labels. The time required to build the tree ${\cal T}$ from one hundred MBs of XML data is a few seconds. In [11] the authors show that given ${\cal T}$ we can compute $\mbox{{\sf XBW}}(d)$ in time linear in the number of tree nodes. In our tests we followed a simpler approach: we represent ${\cal S}_\pi $ as an array of pointers to ${\cal T}$ nodes and we sort ${\cal S}$ operating on this array of node pointers. Experimentally we found that the stable-sorting of ${\cal S}_\pi $ is the most time-consuming part of XBW computation because of the many pointer indirections that generate cache misses. Future work will be devoted to implementing more efficient algorithms, by using insights from the optimal algorithm proposed in [11].


2 Compression of XBW$(d)$: the XBZIP tool

If we are only interested in a compressed (non-searchable) representation of the XML document $d$, we simply need to store the arrays $\widehat{{\cal S}}_{{\sf last}}$, $\widehat{{\cal S}}_\alpha $ and $\widehat{{\cal S}}_{{\sf pcdata}}$ as compactly as possible. This is done by the XBZIP tool whose pseudocode is given in Fig. 4. Experimentally, we found that instead of compressing $\widehat{{\cal S}}_{{\sf last}}$ and $\widehat{{\cal S}}_\alpha $ separately it is more convenient to merge them in a unique array $\widehat{{\cal S}}_\alpha '$ obtained from $\widehat{{\cal S}}_\alpha $ adding a label </ in correspondence of bits equal to 1 in $\widehat{{\cal S}}_{{\sf last}}$. For example, merging the arrays $\widehat{{\cal S}}_{{\sf last}}$ and $\widehat{{\cal S}}_\alpha $ of Fig. 2 yields

\begin{eqnarray*} \widehat{{\cal S}}_\alpha ' & = & \mbox{\small\sf $<$biblio$<$... ...mall\sf$<$title$<$/@id$<$author$<$title$<$/=$<$/=$<$/=$<$/=$<$/} \end{eqnarray*}

This strategy usually offers superior performance in compression because it is able to capture repetitiveness in the tree structure.

As we observed in Sect. 2.2 the arrays $\widehat{{\cal S}}_\alpha '$ and $\widehat{{\cal S}}_{{\sf pcdata}}$ are locally homogeneous since the data descending from a certain tree path is grouped together. Hence, we expect that $\widehat{{\cal S}}_\alpha '$ and $\widehat{{\cal S}}_{{\sf pcdata}}$ are best compressed splitting them in chucks according to the structure of the tree ${\cal T}$. For simplicity in our tests we compress $\widehat{{\cal S}}_\alpha '$ and $\widehat{{\cal S}}_{{\sf pcdata}}$ using the general purpose compressor PPMDI [26]. Somewhat surprisingly this simple strategy already yields good experimental results (see Sect. 4.1).

Figure 4: Pseudocode of XBZIP.

\begin{figure}\hrule {\itemsep=-2pt\baselineskip=12pt\smallskip {{\bf Algorithm}... ...ng {\sc Ppmdi}.} \par\end{enumerate} \vspace*{-2pt}\vskip0pt}\hrule \end{figure}


3 Supporting navigation and search: the XBZIPINDEX tool

In Sect. 2.3 we observed that for navigation and search operations, in addition to $\mbox{{\sf XBW}}(d)$, we need data structures that support rank and select operations over $\widehat{{\cal S}}_{{\sf last}}$ and $\widehat{{\cal S}}_\alpha $. In [11] the authors use rank/select data structures with theoretically efficient (often optimal) worst-case asymptotic performance; in this paper we depart from their approach and use practical methods. In particular, we will view the array as strings, and thus use string indexing techniques. The resulting tool is called XBZIPINDEX and its pseudocode is shown in Fig. 5. Some details follow.

The array $\widehat{{\cal S}}_{{\sf last}}$. Observe that search and navigation procedures only need rank$_1$ and select$_1$ operations over $\widehat{{\cal S}}_{{\sf last}}$. Thus, we use a simple one-level bucketing storage scheme. We choose a constant $L$ (default is $L=1000$), and we partition $\widehat{{\cal S}}_{{\sf last}}$ into variable-length blocks containing $L$ bits set to $1$. For each block we store:


It is easy to see that rank$_1$ and select$_1$ operations over $\widehat{{\cal S}}_{{\sf last}}$ can be implemented by decompressing and scanning a single block, plus a binary search over the table of $1$-blocked ranks.

The array $\widehat{{\cal S}}_\alpha $. Recall that $\widehat{{\cal S}}_\alpha $ contains the labels of internal nodes of ${\cal T}$. We represent it using again a one-level bucketing storage scheme: we partition $\widehat{{\cal S}}_\alpha $ into fixed-length blocks (default is 8Kb) and for each block we store:


Since the number of distinct internal-node labels is usually small with respect to the document size, $\beta$-blocked ranks can be stored without adopting any sophisticated solution. The implementation of $\mbox{{\sf rank}}_\beta(\widehat{{\cal S}}_\alpha , i)$ and $\mbox{{\sf select}}_\beta(\widehat{{\cal S}}_\alpha , i)$ derives easily from the information we have stored.

Figure 5: Pseudocode of XBZIPINDEX.

\begin{figure}\hrule {\itemsep=-2pt\baselineskip=12pt\smallskip {{\bf Algorithm}... ... {\sc FM-index}. \par\end{enumerate} \vspace*{-2pt}\vskip0pt}\hrule \end{figure}

The array $\widehat{{\cal S}}_{{\sf pcdata}}$. This array is usually the largest component of $\mbox{{\sf XBW}}(d)$ (see the last column of Table 1 and Table 3). Recall that $\widehat{{\cal S}}_{{\sf pcdata}}$ consists of the PCDATA items of $d$, ordered according their upward paths. Note that the procedures for navigating and searching ${\cal T}$ do not require rank/select operations over $\widehat{{\cal S}}_{{\sf pcdata}}$ (see Sect. 2). Hence, we use a representation of $\widehat{{\cal S}}_{{\sf pcdata}}$ that efficiently supports XPATH queries of the form /$\Pi $[contains(.,$\gamma $)], where $\Pi $ is a fully-specified path and $\gamma $ is an arbitrary string of characters. To this end we use a bucketing scheme where buckets are induced by the upward paths. Formally, let ${\cal S}_\pi [i,j]$ be a maximal interval of equal strings in ${\cal S}_\pi $. We form one bucket of $\widehat{{\cal S}}_{{\sf pcdata}}$ by concatenating the strings in $\widehat{{\cal S}}_{{\sf pcdata}}[i,j]$. In other words, two elements of $\widehat{{\cal S}}_{{\sf pcdata}}$ are in the same bucket if and only if the have the same upward path. Note that every block will likely be highly compressible since it will be formed by homogeneous strings having the same ``context''.4 For each bucket we store the following information:

Using this representation of $\widehat{{\cal S}}_{{\sf pcdata}}$, we can answer the query /$\Pi $[contains(.,$\gamma $)] as follows (see procedure ContentSearch in Fig 6). By the procedure SubPathSearch we identify the nodes whose upward path is prefixed by $\Pi^R$ (i.e. the reversal of $\Pi $). Then, we identify the substring $\widehat{{\cal S}}_{{\sf pcdata}}[\mbox{\sf F},\mbox{\sf L}]$ containing the labels of the leaves whose upward path is prefixed by =$\Pi^R$. Note that $\widehat{{\cal S}}_{{\sf pcdata}}[\mbox{\sf F},\mbox{\sf L}]$ consists of an integral number of buckets, say $b$. To answer the query, we then search for $\gamma $ in these $b$ buckets using their FM-indexes, taking time proportional to $\vert\gamma\vert$ for each bucket. Since the procedure SubPathSearch takes time proportional to $\vert\Pi\vert$, the overall cost of the query is proportional to $\vert\Pi\vert+b\vert\gamma\vert$.

In addition to the above data structures, we also need two auxiliary tables: the first one maps node labels to their lexicographic ranks, and the second associates to each label $\beta$ the value ${\sf F}[\beta]$. Due to the small number of distinct internal-node labels in real XML files, these tables do not need any special storage method.

Figure 6: Search for the string $\gamma $ as a substring of the textual content of the nodes whose leading path is $\Pi $ (possibly anchored to an internal node).

\begin{figure}\hrule {\itemsep=-2pt\baselineskip=12pt\smallskip {Algorithm {\sf ... ...kets ${\cal B}[i,j]$.\end{enumerate} \vspace*{-2pt}\vskip0pt}\hrule \end{figure}


4 Experimental results

We have developed a library of XML compression and indexing tools based on the XBW transform. The library, called XBZIPLIB, consists of about 4000 lines of C code and runs under Linux and Windows (CygWin). This library can be either included in another software or it can be directly used at the command-line with a full set of options for compressing, indexing and searching XML documents. We have tested our tools on a PC running Linux with two P4 CPUs at 2.6Ghz, 512Kb cache, and 1.5Gb internal memory.

In our experiments we used nine XML files which cover a wide range of XML data formats (data centric or text centric) and structures (many/deeply nested tags, or few/almost-flat nesting). Whenever possible we have tried to use files already used in other XML experimentations. Some characteristics of the documents are shown in Table 1. The following is the complete list providing the source for each file.



Table 1: XML documents used in our experiments. The first three files are data centric, the others text centric. Note that columns $\vert\widehat{{\cal S}}_\alpha \vert$ and $\vert\widehat{{\cal S}}_{{\sf pcdata}}\vert$ report the byte length of these two strings.

DATASET SIZE (BYTES) TREE SIZE #LEAVES TREE DEPTH #TAG/ATTR #MATH195# #MATH196#
MAX/AVG (DISTINCT)
PATHWAYS 79,054,143 9,338,092 5,044,682 10 / 3.6 4,293,410 (49) 24,249,238 36,415,927
XMARK 119,504,522 5,762,702 3,714,508 13 / 6.2 2,048,194 (83) 15,361,789 85,873,039
DBLP 133,856,133 10,804,342 7,067,935 7 / 3.4 3,736,407 (40) 24,576,759 75,258,733
SHAKESPEARE 7,646,413 537,225 357,605 8 / 6.1 179,620 (22) 1,083,478 4,940,623
TREEBANK 86,082,516 7,313,000 4,875,332 37 / 8.1 2,437,668 (251) 9,301,193 60,167,538
XBENCH 108,672,761 7,725,246 4,970,866 9 / 7.2 2,754,380 (25) 7,562,511 85,306,618
SWISSPROT 114,820,211 13,310,810 8,143,919 6 / 3.9 5,166,891 (99) 30,172,233 51,511,521
NEWS 244,404,983 8,446,199 4,471,517 3 / 2.8 3,974,682 (9) 28,319,613 176,220,422

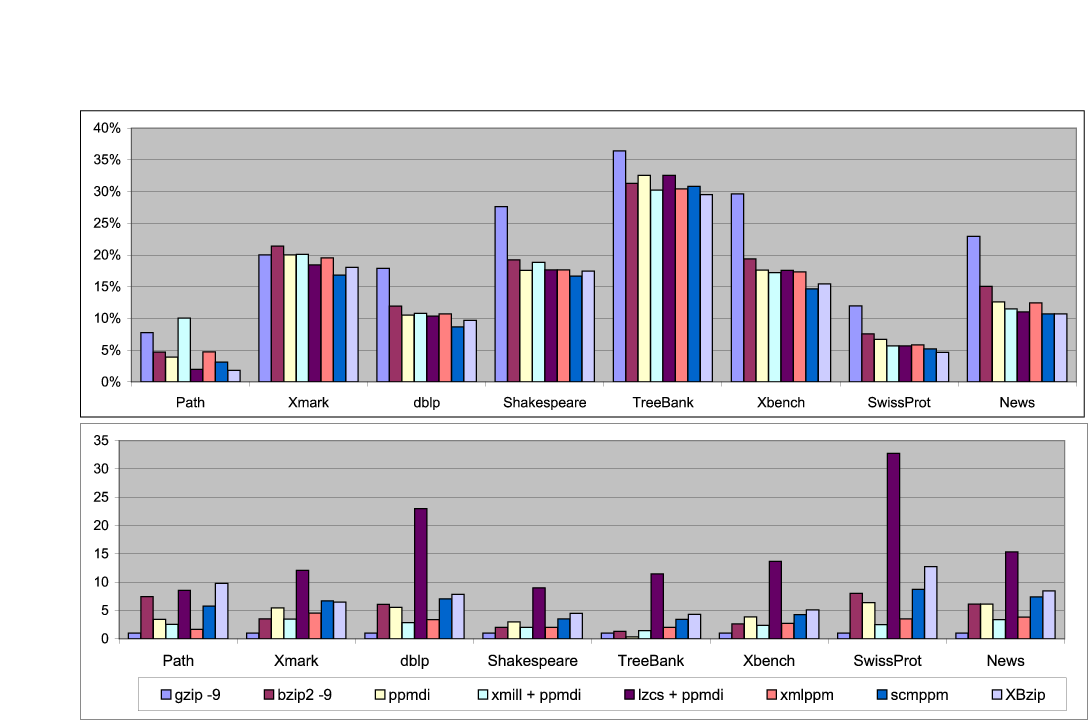
Figure 7: Comparison of XML compressors. Compression ratio (top) and compression time (bottom). Compression times are scaled with respect to GZIP compression time. Note that XMILL, XMLPPM, SCMPPM, and XBZIP all use PPMDI as their base compressor.

Compression Results


1 XML compression

To evaluate the real advantages of XML-conscious tools we compare them with general purpose compressors. The literature offers various general purpose compressors ranging from dictionary-based (GZIP), to block-sorting (BZIP2), and PPM-based compressors (we used PPMDI [26] which is the one with the best performance). In addition, we compare XBZIP with the current state-of-the-art XML-conscious compressors:


We comment on two interesting issues arising from our experiments (see Fig. 7).


In summary, the experimental results show that XML-conscious compressors are still far from being a clearly advantageous alternative to general purpose compressors. However, the experiments show also that our simple XBW-based compressor provides the best compression for most of the files. We think that the new compression paradigm introduced with XBW (i.e. first linearize the tree then compress) is much interesting in the light of the fact that we are simply applying PPMDI without fully taking advantage of the local homogeneity properties of the strings $\widehat{{\cal S}}_\alpha '$ and $\widehat{{\cal S}}_{{\sf pcdata}}$ (see Sects. 2.2 and 3.2). This will be further investigated in a future work.


2 Searching XML compressed files

The literature offers various solutions to index XML files [6]. Here we only refer to XML compression formats that support efficient query operations. In Table 2 we compare our XBZIPINDEX against the best known queriable compressors. We were not able to test XPRESS [23], XGRIND [27] and XQZIP [10], because either we could not find their software or we were unable to run it on our XML files. However, whenever possible we show in Table 2 the performance of these tools as reported in their reference papers.

Table 2: Compression ratio achieved by queriable compressors over the files in our dataset. For XPRESS and XQZIP we report results taken from [23,10] (the symbol - indicates a result not available in these papers). The comparison between the last two columns allows us to estimate the space overhead of adding navigation and search capabilities to XBZIP. Note that we can trade space usage for query time by tuning the parameters of the FM-index [12].

DATASET HUFFWORD XPRESS XQZIP XBZIPINDEX XBZIP
PATHWAYS 33.68 - - 3.62 1.84
XMARK 34.15 - 38 28.65 18.07
DBLP 44.00 48 30 14.13 9.69
SHAKESPEARE 42.08 47 40 21.83 17.46
TREEBANK 67.81 - 43 54.21 29.52
XBENCH 44.96 - - 19.47 15.45
SWISSPROT 43.10 42 38 7.87 4.66
NEWS 45.15 - - 13.52 10.61


From the previous comments and Table 2 we observe that XBZIPINDEX significantly improves the compression ratio of the known queriable compressors by $20\%$ to $35\%$ of the original document size. Table 3 details the space required by the various indexing data structures present in XBZIPINDEX. As expected, the indexing of $\widehat{{\cal S}}_{{\sf last}}$ and $\widehat{{\cal S}}_\alpha $ requires negligible space, thus proving again that these two strings are highly compressible and even a simple compressed-indexing approach, as the one we adopted in this paper, pays off. Conversely, $\widehat{{\cal S}}_{{\sf pcdata}}$ takes most of the space and we plan to improve compression by fine tuning the parameters of the FM-indexes that we use for storing this array (see Sec. 3.3).


Table 3: Percentage of each index part with respect to the corresponding indexed string. Auxiliary info includes all the prefix-counters mentioned in Section 3.3, and it is expressed as a percentage of the total index size. The last column gives an estimate of the avg number of bytes spent for each tree node.

DATASET % INDEX #MATH206# % INDEX #MATH207# INDEX #MATH208# AUXILIARY BYTES PER NODE
PATHWAYS 1.7 0.8 6.0 9.7 0.31
XMARK 3.6 2.5 29.5 7.8 5.94
DBLP 4.9 2.3 32.3 8.1 1.75
SHAKESPEARE 4.6 3.4 32.3 9.7 3.11
TREEBANK 5.2 14.7 68.5 0.2 6.38
XBENCH 4.4 4.7 23.8 0.6 2.74
SWISSPROT 2.2 2.5 14.0 8.0 0.68
NEWS 1.0 0.5 18.5 0.6 3.91

As far as query and navigation operations are concerned, we refer to Table 4. Subpath searches are pretty much insensitive to the document size, as theoretically predicted, and indeed require few milliseconds. Navigational operations (e.g. parent, child, block of children) require less than one millisecond in our tests. As mentioned before, all the others queryable compressors--like XPRESS, XGRIND, XQZIP--need the whole scanning of the compressed file, thus requiring several seconds for a query, and use much more storage space.


Table 4: Summary of the search results for XBZIPINDEX. These time figures do not include the mmapping of the index from disk to internal memory and the loading of the auxiliary infos, which take $0.01$ secs on average. Columns 2, 3, and 4 report the number of blocks accessed during the query and their total size in bytes.

DATASET: QUERY #MATH209# BLOCKS #MATH210# BLOCKS #MATH211# BLOCKS TIME # OCC
(# BYTES) (# BYTES) IN SECS
PATHWAYS: /entry[@id="3"] 5 (5005) 4 (498) 2 $0.007$ 62,414
XMARK /person/address/city[.contains="Orange"] 8 (71324) 6 (1599) 2 $0.008$ 41
DBLP: /article/author[contains="Kurt"] 5 (47053) 4 (1509) 2 $0.001$ 288
DBLP: /proceedings/booktitle[contains="Text"] 5 (21719) 4 (875) 2 $0.002$ 10
DBLP: /cite[@label="XML"] 5 (5005) 4 (473) 134 $0.002$ 7
DBLP: /article/author 5 (47053) 2 (967) 0 $0.008$ 221,289
SHAKESPEARE: /SCENE/STAGEDIR 5 (14917) 2 (1035) 0 $0.002$ 4259
SHAKESPEARE: /LINE/STAGEDIR[contains="Aside"] 5 (21525) 4 (1128) 2 $0.003$ 302
TREEBANK /S/NP/JJ[contains="59B"] 8 (18436) 6 (5965) 697 $0.020$ 2
XBENCH /et/cr[contains="E4992"] 2 (2774) 2 (996) 4 $0.006$ 11
SWISSPROT: /Entry/species[contains="Rattus"] 5 (11217) 4 (1540) 2 $0.002$ 2,154
NEWS: /description[contains="Italy"] 2 (2002) 2 (66) 2 $0.003$ 1,851

5 Concluding Remarks

We have adopted the methods in [11] for compressing and searching labelled trees to the XML case and produced two tools: XBZIP, a XML (un)compressor competitive with known XML-conscious compressors but simpler and with guarantees on its compression ratio; XBZIPINDEX that introduces the approach of using full-text compressed indexing for strings and improves known methods by up to $35\%$ while simultaneously improving the search operations by an order of magnitude.

REFERENCES

[1] http:/xml.coverpages.org/xml.html.

[2] J. Adiego, P. de la Fuente, and G. Navarro.
Lempel-Ziv compression of structured text.
In IEEE Data Compression Conference, 2004.

[3] J. Adiego, P. de la Fuente, and G. Navarro.
Merging prediction by partial matching with structural contexts model.
In IEEE Data Compression Conference, page 522, 2004.

[4] A. Arion, A. Bonifati, G. Costa, S. D'Aguanno, I. Manolescu, and A. Pugliese.
XQueC: pushing queries to compressed XML data.
In VLDB, 2003.

[5] D. Benoit, E. Demaine, I. Munro, R. Raman, V. Raman, and S. Rao.
Representing trees of higher degree.
Algorithmica, 2005.

[6] B. Catania, A. Maddalena, and A. Vakali.
XML document indexes: a classification.
In IEEE Internet Computing, pages 64-71, September-October 2005.

[7] T. Chen, J. Lu, and T. W. Lin.
On boosting holism in XML twig pattern matching using structural indexing techniques.
In ACM Sigmod, pages 455-466, 2005.

[8] J. Cheney.
Compressing XML with multiplexed hierarchical PPM models.
In IEEE Data Compression Conference, pages 163-172, 2001.

[9] J. Cheney.
An empirical evaluation of simple DTD-conscious compression techniques.
In WebDB, 2005.

[10] J. Cheng and W. Ng.
XQzip: Querying compressed XML using structural indexing.
In International Conference on Extending Database Technology, pages 219-236, 2004.

[11] P. Ferragina, F. Luccio, G. Manzini, and S. Muthukrishnan.
Structuring labeled trees for optimal succinctness, and beyond.
In IEEE Focs, pages 184-193, 2005.

[12] P. Ferragina and G. Manzini.
An experimental study of a compressed index.
Information Sciences: special issue on ``Dictionary Based Compression'', 135:13-28, 2001.

[13] P. Ferragina and G. Manzini.
Indexing compressed text.
Journal of the ACM, 52(4):552-581, 2005.

[14] R. F. Geary, R. Raman, and V. Raman.
Succinct ordinal trees with level-ancestor queries.
In ACM-SIAM Soda, 2004.

[15] D. Geer.
Will binary XML speed network traffic?
IEEE Computer, pages 16-18, April 2005.

[16] R. Goldman and J. Widom.
Dataguides: enabling query formulation and optimization in semistructured databases.
In VLDB, pages 436-445, 1997.

[17] A. Golinsky, I. Munro, and S. Rao.
Rank/Select operations on large alphabets: a tool for text indexing.
In ACM-SIAM SODA, 2006.

[18] R. Kaushik, R. Krishnamurthy, J. Naughton, and R. Ramakrishnan.
On the integration of structure indexes and inverted lists.
In ACM Sigmod, pages 779-790, 2004.

[19] R. Kaushik, R. Krishnamurthy, J. F. Naughton, and R. Ramakrishnan.
On the integration of structure indexes and inverted lists.
In ACM Sigmod, 2004.

[20] W. Y. Lam, W. Ng, P. T. Wood, and M. Levene.
XCQ: XML compression and querying system.
In WWW, 2003.

[21] H. Liefke and D. Suciu.
XMILL: An efficient compressor for XML data.
In ACM Sigmod, pages 153-164, 2000.

[22] T. Milo and D. Suciu.
Index structures for path expressions.
In ICDT, pages 277-295, 1999.

[23] Jun-Ki Min, Myung-Jae Park, and Chin-Wan Chung.
Xpress: A queriable compression for XML data.
In ACM Sigmod, pages 122-133, 2003.

[24] E. Moura, G. Navarro, N. Ziviani, and R. Baeza-Yates.
Fast and flexible word searching on compressed text.
ACM Transactions on Information Systems, 18(2):113-139, 2000.

[25] P. R. Raw and B. Moon.
PRIX: Indexing and querying XML using Prufer sequences.
In ICDE, pages 288-300, 2004.

[26] D. Shkarin.
PPM: One step to practicality.
In IEEE Data Compression Conference, pages 202-211, 2002.

[27] P. M. Tolani and J. R. Haritsa.
XGRIND: A query-friendly XML compressor.
In ICDE, pages 225-234, 2002.

[28] H. Wang, S. Park, W. Fan, and P. S. Yu.
ViST: a dynamic index methd for querying XML data by tree structures.
In ACM Sigmod, pages 110-121, 2003.

[29] W. Wang, H. Wang, H. Lu, H. Jang, X. Lin, and J. Li.
Efficient processing of XML path queries using the disk-based F&B index.
In VLDB, pages 145-156, 2005.


Footnotes

....1
Document $d$ may contain tags not including anything, the so called empty tags (i.e. <t/> or <t></t>). These tags are managed by transforming them to <t>$\lambda$</t>, where $\lambda$ is a special symbol not occurring elsewhere in $d$.
... property.2
Readers familiar with the Burrows-Wheeler transform will recognize the analogy: the BWT groups together the characters which are prefixed by the same substring whereas the XBW groups together data enclosed in the same set of tags.
... Clark.3
http:/expat.sourceforge.net/.
... ``context''.4
Notice that XCQ [20] uses a similar partitioning of the PCDATA into data streams, however queries are supported by fully scanning the tree structure properly compressed by exploiting a DTD.
... bucket.5
We used the following parameter settings for the FM-index (cfr [12]): $b=2$Kb, $B=32$Kb and $f=0.05$. These parameters can be tuned to trade space usage for query time.
...PATHWAYS6
http:/www.genome.jp/kegg/xml/
...XMARK7
http:/monetdb.cwi.nl/xml/
...DBLP8
http:/www.cs.washington.edu/research/xmldatasets/
...SHAKESPEARE9
http:/www.ibiblio.org/xml/examples/shakespeare/
...TREEBANK10
http:/www.cis.upenn.edu/~treebank/
...SWISSPROT 11
http:/www.cs.washington.edu/research/xmldatasets/
...NEWS12
http:/www.di.unipi.it/~gulli/
...XMILL13
http:/sourceforge.net/projects/xmill (vers 0.8).
...XMLPPM14
http:/xmlppm.sourceforge.net/.
...SCMPPM15
http:/www.infor.uva.es/~jadiego/download.html.
...LZCS16
http:/www.infor.uva.es/~jadiego/download.html.