Access Control Enforcement
for Conversation-based Web Services
Massimo Mecella1
Dipartimento di Informatica e
Sistemistica, UniversitÓ di Roma ``La Sapienza''
Roma, Italy
mecella@dis.uniroma1.it
Mourad Ouzzani
Cyber Center, Purdue
University
West Lafayette, IN, USA
mourad@cs.purdue.edu
Federica Paci Ouzzani
Dipartimento di Informatica e
Comunicazione, UniversitÓ degli Studi di Milano,
Italy
Milano Italy
paci@dico.unimi.it
Elisa Bertino
CERIAS and Department of
Computer Sciences, Purdue University
West Lafayette, IN, USA
bertino@cerias.purdue.edu
Copyright is held by the World
Wide Web Conference Committee (IW3C2). Distribution of
these papers is limited to classroom use, and personal
use by others.
WWW 2006, May 23.26, 2006, Edinburgh, Scotland.
ACM 1-59593-323-9/06/0005.
ABSTRACT
Service Oriented Computing is emerging as the main approach to build distributed enterprise applications on the Web. The widespread use of Web services is hindered by the lack of adequate security and privacy support. In this paper, we present a novel framework for enforcing access control in conversation-based Web services. Our approach takes into account the conversational nature of Web services. This is in contrast with existing approaches to access control enforcement that assume a Web service as a set of independent operations. Furthermore, our approach achieves a tradeoff between the need to protect Web service's access control policies and the need to disclose to clients the portion of access control policies related to the conversations they are interested in. This is important to avoid situations where the client cannot progress in the conversation due to the lack of required security requirements. We introduce the concept of k-trustworthiness that defines the conversations for which a client can provide credentials maximizing the likelihood that it will eventually hit a final state.
Categories & Subject Descriptors
D.4.6 [Security and Protection]: [Access controls]; K.6.5 [Management of Computing and Information Systems]: Security and Protection - Authentication; H.3.5 [Information Storage and Retrieval]: Online Information Services - Web-based Services
General Terms
Security
Keywords
Web services, Access control, Transition systems, Conversation s
1 Introduction
Service Oriented Computing is poised to be the leading approach to build (distributed) applications on the Web using Web services as the basic building blocks. Web services provide a standard framework for interoperating independently developed Web applications. Generally speaking, a Web service is a set of related functionalities that can be programmatically accessed through the Web. These functionalities represent the different operations made available by the Web service and are described in its service description using the WSDL standard language. While many in the literature treated Web services as a set of independent single operations, interacting with real world Web services involves generally a sequence of invocations of several of their operations, referred to as conversation. A simple example is a bookstore Web service; buying a book involves generally searching for the book, browsing the details and reviews about this book, adding the book to the shopping cart, checking out, paying, etc. It is then important to represent Web services in some formalism that would represent all potential conversations that can take place between the Web service and the client.
As organizations increase their use of Web services and adopt them as the primary tool to build fairly complex distributed systems, security and policy disclosure become crucial [14]. It is well acknowledged that the wide spread adoption of Web services cannot happen without effective solutions for security issues. In this paper, we focus on access control and the limited disclosure of access control policies. An access control model restricts the set of clients or subjects that can invoke Web service's operations. Since clients are not known a priori, we adopt credentials to enforce access control. Credentials are signed assertions describing properties of a subject that are used to establish trust between two unknown communicating parties before allowing access to information or services. Access control policies define rules stating that only subjects with certain credentials satisfying specific conditions can invoke a given operation of the Web service.
While access control has been widely studied in the literature and especially in database systems [7], only recently work on security for Web services has emerged as an important part of the Web service saga [19,15,1,6]. Most approaches in the literature assume a single operation model where operations are independent from each other. Access control is either enforced at the level of the entire Web service or at the level of single operations. In the first approach, the Web service could ask, in advance, the client to provide all the credentials associated with all operations of that Web service. This approach guarantees that a subject will always arrive at the end of whichever conversation. However, it has the drawback that the subject will become aware of all policies on the base of which access control is enforced. Another drawback is that the client may have to submit more credentials than needed. An alternative strategy is to require only the credentials associated with the next operation that the client wants to perform. This strategy has the advantage of asking from the subject only the credentials necessary to gain access to the requested operation. However, the subject is continuously solicited to provide credentials for each transition. In addition, after several steps, the client may reach a state where it cannot progress because the lack of credentials.
It is important to observe that Web service operations represent a coarse-grained process that takes place in the application supporting the Web service and usually involves the consumption of several resources. This shows how important it is for the Web service to maximize the chance that a user would reach a final state to avoid of wasting resources. This should be balanced with the need to retain some control on the disclosure of access policies.
In this paper, we propose a conversation-based access
control model that enables service providers to retain some
control on the disclosure of their access control policies
while giving clients some guarantees on the termination of
their interactions. First, we model all possible
conversations as finite transition systems (aka finite
state machines) [17,4], in which final
states represent those in which the interaction with the
client can be (but not necessarily) ended. Furthermore, our
access control model attempts to maximize the
likelihood that a client reaches a final state
without necessarily having to be made aware of all the
access control policies. We introduce a novel concept of
k-trustworthiness where ![]() can be seen as the level of trust
that a Web service has on a client at any point of their
interaction. The greater the level of trust associated with
a client, the greater is the amount of information about
access control policies that can be disclosed to this
client. The
can be seen as the level of trust
that a Web service has on a client at any point of their
interaction. The greater the level of trust associated with
a client, the greater is the amount of information about
access control policies that can be disclosed to this
client. The ![]() represents the length of the conversations, from
the current state, such that the client is requested to
provide the credentials to invoke any operation along these
paths. All conversations along these paths will eventually
lead to a final state after
represents the length of the conversations, from
the current state, such that the client is requested to
provide the credentials to invoke any operation along these
paths. All conversations along these paths will eventually
lead to a final state after ![]() steps. Thus, the client is assured that its
conversation can eventually terminate. As we shall see,
based on this simple notion of k-trustworthiness,
we are able to develop a flexible (with limited policy
disclosure) access control model for conversation-based Web
services.
steps. Thus, the client is assured that its
conversation can eventually terminate. As we shall see,
based on this simple notion of k-trustworthiness,
we are able to develop a flexible (with limited policy
disclosure) access control model for conversation-based Web
services.
The rest of the paper is organized as follows. Section 2 presents the related work. In Section 3, we present our conversation-based access control model for Web services. In Section 4, we introduce the algorithms used to enforce access control. In Section 5, we describe how the model can be implemented in Web service environments. Finally, in Section 6 we discuss our approach and its advantages. We also identify the major issues in extending our approach to composite services.
2 Related Work
Recent papers [3,4,13] have argued that a Web service is more than a set of independent operations. In fact, during a Web service's invocation, a client interacts with the service performing a sequence of operations in a particular order. Such a sequence is called conversation. Specifically, [3,4] adopt a model based on finite transition systems (aka finite state machines) for representing all possible conversations. The approach of [13] is based on the combined use of two Web service languages, WS-Conversation (WSCL) and WS-Agreement, that allows one to specify non-trivial conversations in which several messages have to be exchanged before the service is completed and/or the conversation may evolve in different ways depending on the state and the needs of the requesting agents and of the service provider.
As far as security issues in Web services are concerned, a fair amount of related research in this area comes from the industry. Two major standards have emerged, namely Security Assertion Markup Language (SAML) and eXtensible Access Control Markup Language (XACML). SAML defines an XML framework for exchanging authentication and authorization information for securing Web services. XACML is an XML framework for specifying access control policies for Web-based resources. Recently it has been extended to specify access control policies for Web services. Other emerging specifications include WS-Security and WS-Policy. WS-Security is a specification for securing SOAP messages using XML Encryption and XML Signature standards and attaching security credentials thereto. WS-Policy is used to describe the security policies in terms of their characteristics and supported features (such as required security tokens, encryption algorithms, privacy rules, etc.).
These proposals do not address the issue of enforcing access control policies. Several approaches [19,15,1,6] suggest some preliminary ideas, but none of them provide a comprehensive solution. [19] proposes two RBAC (Role Based Access Control) models, SWS-RBAC, for single Web services, and CWS-RBAC, for composite Web services. In both models, a service has a few access modes and a role is associated with a list of services which clients, who are assigned that role, have permission to execute. In CWS-RBAC model, the role to which a client is assigned to access a composite service, must be a global role, which is mapped onto local roles of the service providers of the component Web services. [15] proposes an approach for specifying and enforcing security policies. These are specified using a language called WebGuard based on temporal logic and are processed by an enforcement engine to yield site and platform-specific access control. This code is integrated with a Web server and platform specific libraries to enforce the specified policies on a given Web service. [1] presents a Web service architecture for enforcing access control policies expressed in WS-Policy. The architecture is similar to the one proposed in the XACML standard and is characterized by three main components: PDP (Policy Decision Point), PEP (Policy Enforcement Point) and PAP (Policy Administration Point). The PDP realizes the interface between a service and the access control architecture. When a client requests to invoke a service, the service forwards the request to the PDP, which, in turn, sends it to the PEP. The PEP asks to the PAP for the policies applicable to the request and evaluates it against the applicable policies. Then, it returns the final decision to the PDP, which issues the service access.
[6] presents WS-AC1, an access control model with flexible granularity in protecting objects and negotiation capabilities. WS-AC1 is based on the specification of policies stating conditions on the values of the identity attributes and service parameters that a client must provide to invoke the service. Conditions may also be specified against context parameters, such as time. Further, it is possible to define fine-grained policies by associating them with a specific service as well as coarse-grained policies, to be applied to a class of services. The negotiation capabilities of WS-AC1 are related to both identity attributes and service parameters. Through a negotiation process, the client is driven toward an access request compliant with the service description and policies.
The work in [16] considers the issue of modeling and managing trust policies and how to assure that an enforcement system can migrate, during negotiation of trust policies, from a previous and no-more valid set of policies to a new one. Trust policies are modeled as finite state machines, and lifecycle management is obtained by managing such formalization. This work is indeed orthogonal and complementary to our one, even if the basic formalism is the same: our focus is on enforcing access control during service execution, whereas their focus is on modeling and managing trust negotiations. Clearly the two approaches can be merged, e.g., our trust policies can be managed according to their model.
All the previous proposals describe policy-driven access control models. They are based on the enforcement of access control policies stating the requirements to be satisfied by a client to be granted access to a Web service. Since a Web service can be invoked potentially by anyone, the requirements are expressed as conditions on the digital credentials owned by a client. But all these models assume that a Web service provides just a single operation or that all operations are independent.
3 Conversation-based Access Control
In the proposed model, a Web service is characterized by the set of operations that it exports and constraints on the possible conversations it can execute. We compactly represent the service conversations as a finite transition system.
If
![]() ,
we represent this as
,
we represent this as
![]() , and we call
, and we call
![]() the label of the
transition. The transition function can be extended to
finite length sequences of operations or conversations
(traces [17]).
Given a conversation
the label of the
transition. The transition function can be extended to
finite length sequences of operations or conversations
(traces [17]).
Given a conversation
![]() , and two states
, and two states
![]() and
and ![]() , we say that
, we say that
![]() evolves in
evolves in
![]() (represented as
(represented as
![]() ) iff
) iff
![]() such that
such that
![]() and
and
![]() .
.
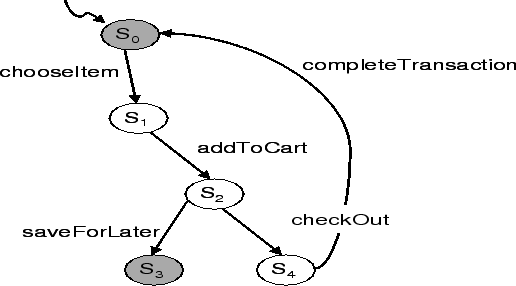
Example 1 Figure 1 represents the transition system of a simple retail Web service eShop, selling some goods. The different labels represent the operations that a client can invoke from any given state and are self-explaining. Final states are represented by gray circles. A client can be involved in different conversations with the service. The client can choose an item (chooseItem), then can add to the cart (addToCart). Further, the client can decide to buy the item (checkOut and then completeTransaction operations) or postpone the purchase (saveForLater) and end the interaction.
Credentials are the mean to establish trust between a client and the service provider. They are assertions about a given client, referred to as the owner, issued by trusted third parties called Certification Authorities (CAs). They are digitally signed using the private key of the issuer CA and can be verified using the issuer's public key. A credential contains typically a set of arbitrary properties characterizing the owner and are specified via (name,value) pairs. Each credential has a type based on the set of attribute names in the credential.
Conditions on the attributes in a credential specify the
security requirements of the service provider. An
attribute condition
![]() is an
expression of the form
is an
expression of the form
![]() op
op ![]() ,
where
,
where
![]() is an attribute name, op is a comparison operator,
and
is an attribute name, op is a comparison operator,
and ![]() is a constant
value in
is a constant
value in
![]() .
We say that a credential
.
We say that a credential
![]() satisfies an attribute condition
satisfies an attribute condition
![]() :
:
![]() op
op ![]() (denoted as
(denoted as
![]() ) if
and only if
) if
and only if ![]()
![]() such that
such that
![]() =
=
![]() in
in
![]() and
and
![]() makes true
makes true
![]() op
op ![]() .
.
We denote with term
![]() a couple
a couple
![]() , where
, where
![]() is a credential type and
is a credential type and
![]() is a set (eventually
empty) of attribute conditions. These attribute conditions
are combined using classical boolean operators.
is a set (eventually
empty) of attribute conditions. These attribute conditions
are combined using classical boolean operators.
The semantics of an access control policy is that, given
a set of credentials
![]() , the access to the operation is granted iff the
credentials satisfies all the attribute conditions (i.e.,
, the access to the operation is granted iff the
credentials satisfies all the attribute conditions (i.e.,
![]() and
and
![]() and
and ![]()
![]() ). As discussed in many logical formalizations (e.g.,
[9,11]), the access to
the Web service operation can be checked through a
reasoning service that verifies if the access request is a
logical consequence of the policy and the credentials.
). As discussed in many logical formalizations (e.g.,
[9,11]), the access to
the Web service operation can be checked through a
reasoning service that verifies if the access request is a
logical consequence of the policy and the credentials.
This definition captures the intuition that a client, owning a set of credentials satisfying a conversation access control policy is granted access to all the operations constituting the conversation. If the conversation is such that it reaches a final state, then the satisfaction of the policy assures that the client will be authorized up to reaching its own goal. The service provider will not be forced to deny access to some operations in the middle of the conversation due to lack of authorization.
Example 1 (CONT.) An example of access control policies for operations addToCart and saveForLater are respectively:
![]()
![]() .
.
![]()
![]() .
.
A trustworthiness level represents the length of a
conversation, from a given state ![]() in the transition system, that leads to a
final state.
in the transition system, that leads to a
final state.
A k-trust policy states the type of credentials and
the conditions on the credential attributes a client, in
state ![]() , must hold in
order to be assigned to a trustworthiness level
, must hold in
order to be assigned to a trustworthiness level ![]() . We use the concept
of trustworthiness level to limit the disclosure of service
provider's access control policies. Therefore, when a
client is assigned the trustworthiness level
. We use the concept
of trustworthiness level to limit the disclosure of service
provider's access control policies. Therefore, when a
client is assigned the trustworthiness level ![]() (on the basis of an
appropriate k-trust policy), the enforcement system asks
only the credentials needed to satisfy all the conversation
access control policies associated with the conversations
from the current state to final states and having length
less or equal to
(on the basis of an
appropriate k-trust policy), the enforcement system asks
only the credentials needed to satisfy all the conversation
access control policies associated with the conversations
from the current state to final states and having length
less or equal to ![]() .
.
Example 1
(CONT.) Let us consider the start state (labeled
with ![]() ) in Figure
1 and determine the potential
conversations. These potential conversations that lead to a
final state and that we need to consider to compute the
k-trustworthiness levels are: (1)
chooseItem
) in Figure
1 and determine the potential
conversations. These potential conversations that lead to a
final state and that we need to consider to compute the
k-trustworthiness levels are: (1)
chooseItem ![]() addToCart
addToCart ![]() saveForLater; (2)
chooseItem
saveForLater; (2)
chooseItem![]() addToCart
addToCart![]() checkOut
checkOut![]() completeTransaction. Adding more
conversations will be useless from access control
perspective since the same conversation will be repeated.
Hence there are 2 different k-trustworthiness levels:
completeTransaction. Adding more
conversations will be useless from access control
perspective since the same conversation will be repeated.
Hence there are 2 different k-trustworthiness levels:
![]() . For
instance, the
. For
instance, the
![]() -trust
policy to assign a client to trustworthiness level
-trust
policy to assign a client to trustworthiness level
![]() is of the form
is of the form
![]() :
it means that if the client is older then eighteen is
entrusted with trustworthiness level
:
it means that if the client is older then eighteen is
entrusted with trustworthiness level ![]() . Such a client has
to fulfill the access control policies associated with the
conversations having length less or equal to
. Such a client has
to fulfill the access control policies associated with the
conversations having length less or equal to ![]() . These
conversations include the following operations:
chooseItem, addToCart, and
saveForLater.
. These
conversations include the following operations:
chooseItem, addToCart, and
saveForLater.
4 Access Control Enforcement
The main feature of the enforcement system
proposed in this paper is that access control is enforced
by considering conversations, thus maximizing the
likelihood that a client reaches a final state and does not
drop off due to lack of authorization. The idea is to
determine, whenever needed and in any step of the
interaction with the client (i.e., at each state of the
transition system), the appropriate trustworthiness
level ![]() to
assign to the client. This requires knowing all potential
trustworthiness levels at any state. The level assigned to
the client is determined based on the k-trust policies. If
the client holds the required credentials, the likelihood
that it will end up to a final state without lacking
authorizations is high. Clearly, the client is not forced
to follow one of the conversations it has been authorized
to; this is why we refer to ``high likelihood'' and not to
``guarantee'' that the client will reach a final state. At
some states of the conversations defined by
to
assign to the client. This requires knowing all potential
trustworthiness levels at any state. The level assigned to
the client is determined based on the k-trust policies. If
the client holds the required credentials, the likelihood
that it will end up to a final state without lacking
authorizations is high. Clearly, the client is not forced
to follow one of the conversations it has been authorized
to; this is why we refer to ``high likelihood'' and not to
``guarantee'' that the client will reach a final state. At
some states of the conversations defined by ![]() , the client may
decide to take a different conversation that is not
included in the ones it has been authorized to, a longer
conversation for example. If this is the case, the current
trustworthiness level
, the client may
decide to take a different conversation that is not
included in the ones it has been authorized to, a longer
conversation for example. If this is the case, the current
trustworthiness level ![]() is recalculated on the basis of the potential
levels at the current state and new credentials are
required.
is recalculated on the basis of the potential
levels at the current state and new credentials are
required.
The challenge now is that given a transition system, we need to determine for each state all possible trustworthiness levels from that state as well as the possible conversations that would define the corresponding access policies. We base our solution on the following observations:
- For an acyclic transition system, the set of potential paths leading from any state to any final state is finite. This set can be easily calculated by a simple traversal of the graph of the transition system.
- If from a given state, a conversation involves a cycle, an infinite number of paths are possible to arrive to a final state within or while traversing this cycle.
- Since we are dealing with access control policies,
usually if an access control policy of an operation
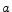 has been
checked against a client, we do not have to check it
again if the client invoke the operation
has been
checked against a client, we do not have to check it
again if the client invoke the operation 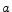 more than
once.
more than
once.
We clearly see that the main difficulties in
traversing the transition system and determining the
potential conversations relate to the existence of cycles.
Before going further, let us introduce the concept of
strongly connected component (SCC for
short). A strongly connected component is the maximal
subgraph of a directed graph such that for every pair of
vertices ![]() ,
,
![]() in the subgraph,
there is a directed path from
in the subgraph,
there is a directed path from ![]() to
to ![]() and a
directed path from
and a
directed path from ![]() to
to ![]() [18]. The
transition system of a Web service can be regarded as a
directed graph where a transition between two states is a
directed edge, without considering the labeling. Based on
the above concept, an acyclic graph can be produced where
nodes represent the different strongly connected components
of the initial graph. This graph is called the directed
graph of the strongly connected components and is
noted
[18]. The
transition system of a Web service can be regarded as a
directed graph where a transition between two states is a
directed edge, without considering the labeling. Based on
the above concept, an acyclic graph can be produced where
nodes represent the different strongly connected components
of the initial graph. This graph is called the directed
graph of the strongly connected components and is
noted
![]() . It
can be efficiently computed through the classical Tarjan's
algorithm [18]
or more recent optimizations, e.g., [12].
. It
can be efficiently computed through the classical Tarjan's
algorithm [18]
or more recent optimizations, e.g., [12].
We can then make the following observations on
this new graph: (i) if the initial
![]() is
acyclic then
is
acyclic then
![]() is
is
![]() itself
[10];
(ii) the nodes that are not involved in cycles will
remain unchanged in the new graph; (iii) cycles will
be ``collapsed'' into strongly connected components and
need to be dealt with in an appropriate way.
itself
[10];
(ii) the nodes that are not involved in cycles will
remain unchanged in the new graph; (iii) cycles will
be ``collapsed'' into strongly connected components and
need to be dealt with in an appropriate way.
For any SCC, we need to determine all possible conversations that will lead from an in-going node, i.e., coming from outside the component, to an out-going node, i.e., going outside the component. These conversations should have the property to cover all potential operations within that strongly connected component. The overall idea of the algorithm which finds all potential k-trustworthiness levels for all states, will be: for a given state, determine all subsequent strongly connected components, including the one to which the current state belongs to. The algorithm will then traverse the transition system from that state and record all conversations leading to a final state. By having computed all possible conversations of all strongly connected components, we will be able to find finite conversations even in the case of cycles.
Before giving the details of the algorithm, we will need to introduce several concepts.
An object type
SetOf<element>2for representing
a set of <element>s, where
<element> can be whichever other object
type. We use the term set in a proper way, to mean a
collection of elements without repetitions and without any
order. We assume the availability of the = operator on
sets, which compares two homogeneous sets for equality, a
method add(<element> e) for adding a new
element, and ![]() for calculating its dimension (number
of elements). An object type Sequence is defined
for representing conversations. On such a type, two methods
are defined: (i) length() returns the
length of the sequence, and (ii) set()
for calculating its dimension (number
of elements). An object type Sequence is defined
for representing conversations. On such a type, two methods
are defined: (i) length() returns the
length of the sequence, and (ii) set()
![]() SetOfOperation returns the set of all the distinct
operations. As an example,
SetOfOperation returns the set of all the distinct
operations. As an example, ![]() .set() =
.set() =
![]() =
=
![]() .set().
.set().
The directed graph of the strongly connected components of the original transition system is defined as follows:
![]() :
c is a strongly connected component in
:
c is a strongly connected component in
![]() ;
;
![]() :
:
![]()
![]()
![]() and
and
![]() ,
,
![]() ,
,
![]() such that
such that
![]()
Given a state
![]() ,
we refer to the node of
,
we refer to the node of ![]() associated to the strongly connected
component of
associated to the strongly connected
component of ![]() as
as
![]() ; we also say
that
; we also say
that ![]() is the
image of
is the
image of ![]() .
.
In the algorithms presented in the following, we
assume an object type GraphSCC, defined for
representing a graph of SCC. On the type
GraphSCC, a method projection(Node c)
![]() GraphSCC is defined, that takes as input a node
GraphSCC is defined, that takes as input a node
![]() and returns a new
subgraph obtained by considering
and returns a new
subgraph obtained by considering ![]() and all nodes reachable by it, i.e., it is
the subgraph obtained by visiting depth-first the graph
starting from
and all nodes reachable by it, i.e., it is
the subgraph obtained by visiting depth-first the graph
starting from ![]() .
.
For each node/SCC of
![]() , we
know the number of different operations that label
transitions among the associated states of
, we
know the number of different operations that label
transitions among the associated states of
![]() . More
specifically, for each SCC
. More
specifically, for each SCC ![]() , the set
, the set
![]() =
= ![]()
![]() such that
such that
![]() and
and
![]() =
= ![]() =
= ![]()
![]() can be easily
determined. The cardinality of
can be easily
determined. The cardinality of ![]() is referred to as
is referred to as ![]() . If the
connected component
. If the
connected component ![]() is the image of a single state of
is the image of a single state of
![]() , then
its
, then
its
![]() . On the
type GraphSCC, we define a method card(Node c)
. On the
type GraphSCC, we define a method card(Node c)
![]() Integer that takes as input a node
Integer that takes as input a node ![]() and returns its
cardinality.
and returns its
cardinality.
For each node/SCC of
![]() ,
the longest path, among the shortest ones that (i)
starting from an in-going node finish in a distinct
out-going node, and (ii) comprise all the different
operations in
,
the longest path, among the shortest ones that (i)
starting from an in-going node finish in a distinct
out-going node, and (ii) comprise all the different
operations in ![]() , is considered. More specifically, for each
SCC
, is considered. More specifically, for each
SCC ![]() , a sequence of operations
, a sequence of operations ![]() is said to be
covering iff
is said to be
covering iff
![]() with
with
![]() in-going state of
in-going state of
![]() and
and ![]() out-going state
(
out-going state
(![]() =
= ![]() =
= ![]() ) AND
) AND
![]() .set() =
.set() =
![]() . We use the
notation
. We use the
notation
![]() for
referring to a traversing sequence of operations3. Then for each
SCC
for
referring to a traversing sequence of operations3. Then for each
SCC ![]() , a set
, a set
![]() is
defined:
is
defined:
![]() =
=
![]()
![]() such that: (
such that: (
![]() for
for
![]() )
AND (
)
AND (
![]() with
with ![]() =
= ![]() then
then
![]() .length()
.length()
![]() .length())
.length())
![]() . We denote
coverage(
. We denote
coverage(![]() ) = max(
) = max(
![]() ).
).
The coverage of a SCC can be calculated by generating by enumeration, which can be done with a simple recursion, all the paths from any in-going node to an out-going one. A global array of boolean variables, with dimension equal to the number of distinct out-going nodes is used to record whether the out-going node has been reached, and another global array of integer variables maintains the length of the sequence that evolves the in-going node up to the out-going one. As soon as all the boolean variables are set to true, meaning that we have found the shortest paths, then the maximum among the values in the other array is calculated. In order to close all the recursive instances, each of them is controlled by a condition on the conjunction of all the boolean array's values.
On the type GraphSCC, a method
coverage(Node c)
![]() Integer is defined, that takes as input a node
Integer is defined, that takes as input a node
![]() and returns its
coverage.
and returns its
coverage.
For each node/SCC of
![]() , we
define the rank as follows:
, we
define the rank as follows:
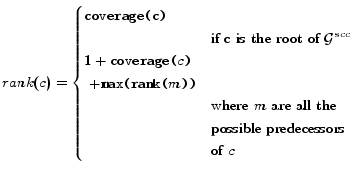 |
As
![]() is
acyclic, the rank of each node can be computed in three
steps: (i) by running a depth-first-search
algorithm, and for each visited node to push on a stack a
record, labeled with the node, containing the predecessor
node; (ii) then by popping the stack, and for each
encountered record, to remove from the stack all the
records with the same state, by recording the corresponding
predecessor node, and to push in another stack the formula
for calculating the rank (at this point the predecessors
are all correctly identified); (iii) finally, by
popping the second stack, and for each removed record, we
calculate the rank. We should observe that the stack now
gives the exact order according to which to calculate the
formulas: each removed record gives the values to be used
in following records.
is
acyclic, the rank of each node can be computed in three
steps: (i) by running a depth-first-search
algorithm, and for each visited node to push on a stack a
record, labeled with the node, containing the predecessor
node; (ii) then by popping the stack, and for each
encountered record, to remove from the stack all the
records with the same state, by recording the corresponding
predecessor node, and to push in another stack the formula
for calculating the rank (at this point the predecessors
are all correctly identified); (iii) finally, by
popping the second stack, and for each removed record, we
calculate the rank. We should observe that the stack now
gives the exact order according to which to calculate the
formulas: each removed record gives the values to be used
in following records.
Finally, on the type GraphSCC, a method
rank(Node c)
![]() Integer is defined, that takes as input a node
Integer is defined, that takes as input a node
![]() and returns its
rank.
and returns its
rank.
We can now present the algorithms for computing,
for each state of the Web service transition system, the
possible k-trustworthiness levels and the conversations
corresponding to them. These algorithms assume some global
variables, on which all instances of the recursion have
shared access. These variables are the transition system
![]() of type
TS, the
of type
TS, the
![]() of type
SetOfPolicy that, for each operation, report the
corresponding access control policy
of type
SetOfPolicy that, for each operation, report the
corresponding access control policy ![]() (of type
Policy), the
(of type
Policy), the
![]() (of
type GraphSCC) and a
(of
type GraphSCC) and a ![]() (of type SetOfSequence), which
is built during the execution of the algorithms, and
represents the set of conversations defining the
k-trustworthiness levels.
(of type SetOfSequence), which
is built during the execution of the algorithms, and
represents the set of conversations defining the
k-trustworthiness levels.

|
The isNewString() is a method defined on
the object type Sequence.

|
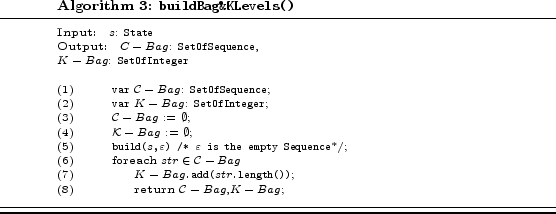
|
The overall algorithm builds, for each state of the Web service transition system, the k-trustworthiness levels and the corresponding conversations.
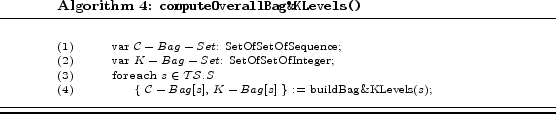
|
Now that for each state we computed all potential k-trustworthiness levels and corresponding conversations (from which to derive conversation policies), the access control enforcement system can proceed through the following phases:
- Bootstrapping phase - This phase occurs when
the subject has its first contact with the Web service.
The enforcement system assigns the initial level of
trustworthiness
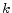 , amongst all possible ones (as computed
previously), based on the set of initial credentials
provided by the client (e.g., the IP address of the
client) and the trust policies of the Web service. If the
initial credentials are not sufficient, the access
control system assigns to the client the smallest
trustworthiness level, or a default level
, amongst all possible ones (as computed
previously), based on the set of initial credentials
provided by the client (e.g., the IP address of the
client) and the trust policies of the Web service. If the
initial credentials are not sufficient, the access
control system assigns to the client the smallest
trustworthiness level, or a default level 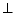 (meaning
step-by-step access control), or refuses the access,
depending on the trust policies.
(meaning
step-by-step access control), or refuses the access,
depending on the trust policies. - Once the access control enforcement system assigns a
trustworthiness level
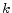 to the client, it will ask the client to provide
all the required credentials based on the associated
access policies computed by the previous algorithm.
to the client, it will ask the client to provide
all the required credentials based on the associated
access policies computed by the previous algorithm. - If the subject provides the requested credentials, it
can invoke all operations on paths less or equal to
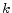 that lead to
final states.
that lead to
final states. - If from a given state, the client decides to continue its interaction with the Web service through a path different from those assigned by its k-trustworthiness level, then a new k-level of trust needs to be computed and assigned to the client. The process will then continue as before until the client decides to stop.
5 Architecture of the Enforcement System
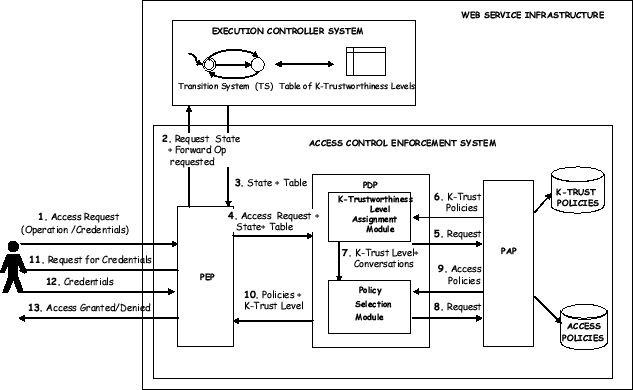
This section describes how the proposed access control model for conversation-based Web services can be implemented in Web service environments. The system architecture is depicted in Figure 3. To be compliant with the XACML standard, the access control enforcement system is composed of a Policy Enforcement Point (PEP), a Policy Decision Point (PDP) and a Policy Administration Point (PAP). The PEP realizes the interface with clients and with the Execution Controller System (ECS) [2]. The ECS is not part of the enforcement system: it maintains a copy of the transition system to keep track of the state of the conversation between the client and the service. Further, at deployment time, it generates a table reporting for each state the k-trustworthiness levels.
The PEP intercepts all the access requests submitted by clients, specifying the name of an operation the client wants to perform and/or a set of credentials.
The first request that a client sends to the PEP
contains both a name of an operation and a set of
credentials (step 1). Once received, the PEP contacts the
ECS to provide it information about the operation
requested, so it can update the state of the conversation
and can return it to the PEP with the table (steps 2-3).
Then, the PEP reformulates the access request adding
information about the current state of the conversation and
the table and sends it to the PDP (step 4). The PDP's
k-Trustworthiness Level Assignment (TLA) Module, having
received from the PEP the information about the current
state of the conversation and the table, queries the table
to select the trustworthiness levels
![]() .
Hence, the TLA module interacts with the PAP which manages
the policies, to retrieve the k-trust policies associated
with trustworthiness levels
.
Hence, the TLA module interacts with the PAP which manages
the policies, to retrieve the k-trust policies associated
with trustworthiness levels
![]() (step 5-6) and evaluates if the credentials provided by the
client in the request satisfy one of the policies. If this
is the case, the client is assigned to the trustworthiness
level
(step 5-6) and evaluates if the credentials provided by the
client in the request satisfy one of the policies. If this
is the case, the client is assigned to the trustworthiness
level ![]() associated
with the
associated
with the ![]() -trust
policy he is compliant with. Once assigned the
trustworthiness level
-trust
policy he is compliant with. Once assigned the
trustworthiness level ![]() , the TLA sends it with the associated
conversations to the PDP's Policy Selection (PS) module
(step 7). The PS module asks the PAP for the access control
policies related to the operations constituting the
conversations, that the client may engage with the service
on the basis of the assigned trustworthiness level
, the TLA sends it with the associated
conversations to the PDP's Policy Selection (PS) module
(step 7). The PS module asks the PAP for the access control
policies related to the operations constituting the
conversations, that the client may engage with the service
on the basis of the assigned trustworthiness level
![]() (steps 8-9).
Then, the PS module combines the selected policies to
obtain the corresponding conversation access control
policy. Hence, it returns the policies to the PEP with
(steps 8-9).
Then, the PS module combines the selected policies to
obtain the corresponding conversation access control
policy. Hence, it returns the policies to the PEP with
![]() (step 10). At
this point, the PEP asks to the client to provide the
credentials required by the policies and evaluates them
against the policies (steps 11-12). If the check is
positive, the client can perform any operation in the
conversations related to the trustworthiness level
(step 10). At
this point, the PEP asks to the client to provide the
credentials required by the policies and evaluates them
against the policies (steps 11-12). If the check is
positive, the client can perform any operation in the
conversations related to the trustworthiness level
![]() . Since the PEP
stores a copy of the table of trustworthiness levels and
the level
. Since the PEP
stores a copy of the table of trustworthiness levels and
the level ![]() assigned to the client, when it submits a request to
perform an operation, which does not belong to the allowed
conversations, the PEP contacts the PDP, which assigns a
new trustworthiness level to the client. In this case, the
PEP does not send again the table of trustworthiness
levels, but only the state of the conversation with the
client, which is necessary to select from the table the
trustworthiness levels associated with that
state.
assigned to the client, when it submits a request to
perform an operation, which does not belong to the allowed
conversations, the PEP contacts the PDP, which assigns a
new trustworthiness level to the client. In this case, the
PEP does not send again the table of trustworthiness
levels, but only the state of the conversation with the
client, which is necessary to select from the table the
trustworthiness levels associated with that
state.
The main advantage of the proposed architecture is that is in conformity with the reference standard for access control in distributed systems, XACML. Further, it is modular and allows an easy integration of the access control system in Web service frameworks. Finally, the enforcement system is independent from the language used to express k-trust and access control policies. Both WS-Policy and the XACML Profile for Web services can be used to represent the policies characterizing our model.
6 Discussion and Future Work
In this paper, we presented a novel approach to deal with access control in conversation-based Web services. Our first contribution is to consider access control in Web services as transition systems instead of systems that present sets of independent operations. As we mentioned earlier, most existing access control approaches assume a single operation model for Web services where the invocation of operations are independent from each other.
Moreover, as mentioned previously, two extreme approaches regarding the disclosure of access policies are possible: (1) requesting all the credentials needed for all the operations, and (2) requesting credentials related to each operation the client is interested in invoking. In this context, our second objective was to strike a balance between the need to reveal only part of the Web service access policy and the need to offer enough assurance to clients that they can reach a final state.
In order to support such claims, we develop a
very simple model for measuring the two parameters risk and
disclosure. Given a Web service operation ![]() , we consider
, we consider
![]() as the
probability that the client DOES NOT have
the credential(s) satisfying the access control policy
guarding the operation.
as the
probability that the client DOES NOT have
the credential(s) satisfying the access control policy
guarding the operation.
In general, the risk associated to an event is
the product of the probability that the event happens and
the damage produced by the event. In simple terms, the
damage of having the client dropping off due to lack
of authorization is the number of executed operations.
Indeed, executing an operation requires resources to the
service provider, and if the conversation is suddenly
interrupted in a non-final state, all these resources have
been ``wasted''. In addition, the leakage in terms
of disclosure of access control policies is proportional to
the operations already executed. We now evaluate these two
simple metrics risk and leakage faced by a service provider
during a conversation
![]() .
.
In a step-by-step enforcement, the risk faced
before involving the ![]() -th operation (
-th operation (![]() being the next operation for which the client
may not posses the required credential to access to)
is:
being the next operation for which the client
may not posses the required credential to access to)
is:
Similarly, the leakage after executing the
In this case, the client may be an attacker that voluntarily drop-off the conversation after accessing the previous policies.
In our conversation-based enforcement, assuming
that the conversation ![]() is the one for which the service provider has
requested all the credentials, we have:
is the one for which the service provider has
requested all the credentials, we have:
Indeed during the conversation, the various invocations of Web service operations are somehow independent. Thus, the probability that a client has all the credential(s) needed to access all the operations is simply
Since the enforcement system has required all the credentials at the beginning, the leakage is:
Table 1 summarizes
the risk and leakage, after the conversation ![]() , for our
approach and for a step-by-step approach assuming that all
, for our
approach and for a step-by-step approach assuming that all
![]() are equals,
i.e,
are equals,
i.e,
![]() .
.
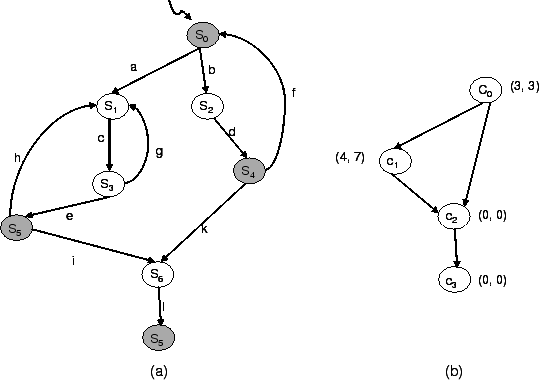
Let us now compare the possible approaches to access control enforcement on a simple Web service having the behavior represented as in Figure 4.
Table 2 shows the
results for the step-by-step enforcement, the
conversation-based (with the 2 possible k-levels, 2 and 4),
and the request-all approach. We consider both possible
conversations. Specifically, in the case of the
conversation ![]() ,
with the client assigned a k-level of 2, if after one step
the client chooses an operation it has not been authorized
yet, and it is assigned a k-level of 4 - the only possible,
the risk is given by the damage - 1 step - for 3
,
with the client assigned a k-level of 2, if after one step
the client chooses an operation it has not been authorized
yet, and it is assigned a k-level of 4 - the only possible,
the risk is given by the damage - 1 step - for 3
![]() (the
probability of not having the credential for the remaining
3 steps).
(the
probability of not having the credential for the remaining
3 steps).
|
Hence, it becomes clear that the k-trustworthiness level model is a trade-off between the request-all approach, that always minimizes the risk by maximizing the disclosure, and the step-by-step, which minimizes the disclosure by maximizing the risk. If good client profiles (obtained by logs, etc.) are available, the trust policies can be fine tuned to have most of the clients assigned to the correct k-trustworthiness level, i.e., the one that effectively the client will follow, thus obtaining the best of the two extreme approaches.
Table 3 summarizes the advantages and disadvantages of the different approaches regarding access control and disclosure of access policies. It shows that our solution takes a more balanced approach and provides more flexibility. On one hand, it gives some guarantees to the client that once it provides the requested credentials, it will eventually reach a final state. On the other hand, the Web service retains some control on the disclosure of its access policy.
|
As part of our future work we would like to integrate our approach with an exception-based mechanism tailored to support access control enforcement. In particular, in a step-by-step approach, whenever a client cannot complete a conversation because of the lack of authorization, some alternative actions and operations are taken by the Web service. A typical action would be to suspend the execution of the conversation, ask the user to acquire the missing credentials, and then resume the execution of the conversation; such a process would require investigating a number of issues, such as determining the state information that need to be maintained, and whether revalidation of previous authorizations is needed when resuming the execution. A different action would be to determine whether alternative operations can be performed to replace the operation that the user cannot execute because of the missing authorization. We would like to develop a language according to which one can express the proper handling of error situations arising from the lack of authorization.
A natural next step for our work is to extend it to composite services. We need composition when a client request cannot be satisfied by any available service, but by suitably combining parts of available Web services. Composition involves usually two different issues [5]: synthesis is concerned with synthesizing a specification of how to coordinate the component services to fulfill the client request; orchestration relates to the enactment of the composite service and the coordination among services, by executing the specification produced by the composition synthesis.
Access control needs to be addressed at the orchestration level to manage the client's credentials needed to access the different service components and the access policies of these services. The objective is to extend the notions of conversation access control policy and k-trustworthiness to composite services. We are still assuming a conversation-based model for Web services. In addition, all component services support our k-trustworthiness model. Thus each service compute a local k or trust level and the challenge would be to compute a global trust level in an effective and efficient way. We need to determine the credentials to request from the client that will lead to a final state.
Web services may fail or ask for credentials that cannot be provided by clients. In addition to the ideas presented earlier on suspending the current conversation or replacing the operations, another potential approach is to devise a substitutability scheme [8] where the ``failing'' service is substituted with a new Web service that has at least the same behavior and that is access control-compatible with the composite service and the current state. This would require addressing several challenging issues including computing a new global trust level, deriving new credentials from existing ones, and devising techniques on how to deal with the work done so far by the Web service being substituted.
Acknowledgments
The work of Massimo Mecella was partly supported by the European Commission (FP6-2004-IST-4-027517 project SEMANTICGOV) and the Italian MIUR (RBNE0193K5_002 FIRB 2001 project MAIS, RBNE0358YR_003 FIRB 2003 project EG4M). The work of Mourad Ouzzani was partly supported by Lilly Endowment, NSF-ITR 0428168 and US DHS PURVAC. The work of Federica Paci was partly funded by the European Commission under the Contract 001945, Integrated Project TRUSTCOM. The work of Elisa Bertino was partly supported by the NSF under Grant No. 0430274 and the sponsors of CERIAS.
REFERENCES
[1]C. Ardagna, E. Damiani, S. De Capitani di Vimercati, and P. Samarati, A web service architecture for enforcing access control policies, In Proceedings of 1st International Workshop on Views on Designing Complex Architectures, 2004
[2] B. Benatallah, F. Casati, H. Skogsrud, and F. Toumani, Abstracting and enforcing web service protocol, International Journal of Cooperative Information Systems, 13(4), 2004
[3] B. Benatallah, F. Casati, and F. Toumani, Web service conversation modeling: A cornerstone for e-business automation, IEEE Internet Computing, 8(1):46 - 54, 2004
[4] D. Berardi, D. Calvanese, G. De Giacomo, M. Lenzerini, and M. Mecella, Automatic service composition based on behavioral descriptions, International Journal of Cooperative Information Systems, 14(4):333 - 376, 2005
[5] D. Berardi, D. Calvanese, G. De Giacomo, R. Hull, and M. Mecella, Automatic composition of transition-based semantic web services with messaging, In Proc. VLDB 2005
[6] E. Bertino, L. Martino, F. Paci, and A. Squicciarini, An adaptive access control model for web services, To appear on International Journal of Web Services Research (JWSR), 2006
[7] E. Bertino and R. Sandhu, Database security. Concepts, approaches, and challenges, IEEE Transaction on Dependable and Secure Computing, 2(1), January-March 2005
[8]L. Bordeaux, G. SalaŘn, D. Berardi, and M. Mecella, When are two web services compatible?, In Technologies for E-Services, 5th International Workshop, TES 2004, Toronto, Canada>, August 2004
[9] S. De Capitani di Vimercati and P. Samarati, Access control: policies, models and mechanisms, In R. Focardi and F. Guerrieri, editors, Foundations of Security Analysis and Design - Tutorial Lectures, volume 2171 of LNCS, Springer Verlag, 2001
[10]A. Dovier, C. Piazza, and A. Policriti, An efficient algorithm for computing bisimulation equivalence, Theoretical Computer Science, 311(1-3):221-256, 2004
[11] H. Koshutanski and F. Massacci, Interactive credential negotiation for stateful business processes, In Proc. iTrust 2005, 2005
[12] E. Nuutila and E. Soisalon-Soininen, On finding the strongly connected components in a directed graph, Information Processing Letters, 49:9-14, 1993
[13] S. Paurobally and N. R. Jennings, Protocol engineering for web services conversations, Engineering Applications of Artificial Intelligence, 18, 2005
[14] Kent E. Seamons, M. Winslett, and T. Yu, Limiting the disclosure of access control policies during automated trust negotiation, Proceedings of the Network and Distributed System Security Symposium, San Diego, California, USA, 2001
[15] E.G. Sirer and K. Wang, An access control language for web services, In Proc. ACM SACMAT 2002
[16] H. Skogsrud, B. Benatallah, and F. Casati, Trust-serv: model-driven lifecycle management of trust negotiation policies for web services, Proc. World Wide Web Conference 2004
[17] C. Stirling, Modal and temporal logics for processes, In F. Moller and G.M. Birtwistle, editors, Logics for Concurrency. Structure versus Automata (8th Banff Higher Order Workshop, 1995, Proceedings), volume 1043 of LNCS, Springer Verlag, 1996
[18] R.E. Tarjan, Depth-first search and linear graph algorithms, SIAM Journal on Computing, 1:146-160, 1972
[19] R. Wonohoesodo and Z. Tari, A role based access control for web services, In Proc. SCC 2004, 2004
Footnotes
- 1 This work was performed while visiting research assistant at CERIAS and Department of Computer Sciences, Purdue University, USA.
- 2 In the following, we use Type for indicating object types, and object for indicating object instances.
- 3
A traversing sequence is not necessarily an Eulerian
path of
 ,
whereas each Eulerian path, if it exists, is a traversing
sequence. This is why we do not impose the uniqueness of
an edge.
,
whereas each Eulerian path, if it exists, is a traversing
sequence. This is why we do not impose the uniqueness of
an edge.