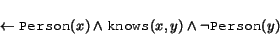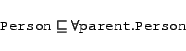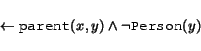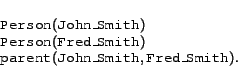Position Paper:
A Comparison of Two Modelling Paradigms
in the Semantic Web

Peter F. Patel-Schneider

Bell Labs Research
Lucent Technologies

pfps@research.bell-labs.com

Ian Horrocks

School of Computer Science
University of Manchester

horrocks@cs.man.ac.uk

Copyright is held by the World Wide Web Conference Committee (IW3C2). Distribution of these papers is limited to classroom use, and personal use by others.
WWW 2006, May 23.26, 2006, Edinburgh, Scotland.
ACM 1-59593-323-9/06/0005.

Abstract:

Classical logics and Datalog-related logics have both been proposed as underlying formalisms for the Semantic Web. Although these two different formalism groups have some commonalities, and look similar in the context of expressively-impoverished languages like RDF, their differences become apparent at more expressive language levels. After considering some of these differences, we argue that, although some of the characteristics of Datalog have their utility, the open environment of the Semantic Web is better served by standard logics.

Categories & Subject Descriptors

I.2.0 [Computing Methodologies]: Artificial Intelligence - General
I.2.4 [Computing Methodologies]: Artificial Intelligence - Knowledge Representation Formalisms and Methods

General Terms

Design, Languages

Keywords

Semantic Web, philosophical foundations, representation, modelling

1 Introduction

Two very different modelling paradigms have been proposed for the Semantic Web. One paradigm is based on notions from standard logics, such as propositional logic, first-order logic, and Description Logics [2]. This paradigm is embodied in the W3C-recommended Semantic Web languages the Resource Description Framework (RDF) [28], RDF Schema [5], and the OWL Web Ontology Language [8]. (We will call this paradigm the Classical paradigm.) The other paradigm is based on notions from object-oriented databases [1] and rule languages [33]. This paradigm is embodied in a previous version of RDF [30] and several proposals for Semantic Web languages, including OWL Flight [6]. (We will call this paradigm the Datalog paradigm.)

The best versions of both paradigms can be given formal definitions. The formal definition for the Classical paradigm comes from the standard model-theoretic basis for Classical logics, as exemplified in the model theories for both RDF [20] and OWL [31]. For the Datalog paradigm, various versions of the Datalog formal basis [33] can be given, including formal bases that incorprate non-monotonic extensions to Datalog [17,16].

There are significant differences between the two paradigms. These differences range from computational aspects of the paradigms, in various guises; to the expressive power of the paradigms; to the naturalness of modelling in the paradigms. Competing claims have been made concerning which of the two paradigms are better for representation and reasoning in the Semantic Web.

A recent paper by de Bruijn et al [7] has argued in favour of the Datalog paradigm, as embodied in OWL Flight. In this paper we argue that the paradigm based on standard logical notions is a better paradigm for the Semantic Web than the Datalog paradigm. We are not (just) arguing that OWL DL is better than OWL Flight. Instead we are arguing that the notions underlying standard logics are better suited to the Semantic Web than those underlying Datalog.

2 The Semantic Web

The World Wide Web has been a tremendous success, making an incredible range of information and services accessible to billions of users worldwide. In some respects, however, the Web is a victim of its own success, as it has become more and more difficult to manage the ever-increasing volume of available data, and to use it to perform more complex tasks than keyword based search and retrieval.

This problem is exacerbated by the unstructured nature of the web, and the focus of HTML on presentation rather than content. It has been suggested that Web resources could be made much more usable if ``information was given a well defined meaning'' [4] so that it formed a ``logical web of data'' [3]; this idea/dream has become known as the Semantic Web.

Early work on realising the Semantic Web has focused on the development of languages such as RDF and OWL that could be used both to augment web content with ``semantic markup'' and to establish ontologies--vocabularies of terms with formally specified and machine accessible meanings that can be used in semantic markup.

One of the key factors in the success of the existing Web is its decentralised nature; this allows the Web to grow rapidly (sometimes in unforseen directions) without the inertia that would inevitably result from the need to coordinate with a centralised authority. As an extension of the existing Web, the Semantic Web will have to exist within the same loosely organised framework, and so without the benefit of canonical names or authoritative sources of meaning: there may be many ontologies providing different, perhaps even conflicting, meanings for the same term. Using formal languages to define ontologies will mean, however, that such differences can be detected and analysed.

Throughout the rest of the paper we will appeal to characteristics of the Semantic Web in our comparison. To illustrate these characteristics, we will employ examples of information situated in the Semantic Web. The first example involves information from a modified and extended version of Friend of a Friend (FOAF) information.¹ We use a modified and extended version of FOAF, as some of the differences between the two pardigms only show up in more expressive representation formalisms than the formalism implicitly used in FOAF. We will also use information from an extended version of the airline flight example in de Bruijn et al [7]. These two kinds of information have different characteristics, with the first being very open and decentralized and the second being somewhat more closed and centralized.

Throughout the paper we will be using a hybrid, informal notation for formulae (including rules), taking bits of syntax commonly used in accounts of first-order logic, Datalog, and Description Logics. We will use italicised letters (e.g., $x$) for variables, with implicit universal quantification in rules. Constants and properties will be written in typewriter font (e.g., mother).

3 The Two Paradigms

3.1 The Classical Paradigm

The Classical paradigm, embodied in RDF and OWL, has its formal basis in standard model-theoretic accounts of logic. The basic idea here, without going into too much detail, is that the domain being modelled is abstractly represented as a set of objects and relationships between them. There can be many (often potentially infinite) states of affairs, often called interpretations or models, each describing one possible state of the domain. For example, if we are modelling FOAF relationships, a person ``Sam'' might be represented by an object, and relationships like ``knowing someone else'', ``authoring a paper'', ``parent'', and ``married to'' by relations between (in this case pairs of) objects. In the absence of any other information, there are interpretations for every possible way that the objects can be related by the relations, including all sorts of nonsensical relationships such as a person authoring another person.

Ontologies consist of sets of statements (often called axioms) that describe characteristics that must be satisfied by (the ontology designer's idea of) ``reasonable'' states of the world. Formally, such statements correspond to logical sentences, and an ontology corresponds to a logical theory. For example, our extended FOAF ontology might include axioms with the effect that there is a class of people, that the married relation has domain and range of person, and that all persons have exactly two parents, both of whom are themselves persons. Such an ontology would rule out interpretations where people had three parents, or where one of their parents is not a person. A ``perfect'' ontology, if such a thing were ever possible, would admit all reasonable interpretations and rule out all unreasonable ones. Note that this does not mean that only one interpretation would remain--our ontology may, for example, precisely describe the characteristics of familial relationships without saying anything about who is the parent of whom. Further details of this model-theoretic account of meaning are not relevant to this paper. What is relevant is that this account admits a multiplicity of (hopefully ``reasonable'') interpretations, leaving open which one is the actual situation.

Information (e.g., an ontology) is separate from interpretations in this paradigm. The meaning of information is carried in the mapping between the information and the interpretations that are consistent with the information. It is thus often useful here to think of the meaning of information as corresponding to the set of interpretations that are consistent with the information. Query answering in this paradigm comes down to the task of checking if some situation holds in all interpretations that are consistent with the available information (i.e., logical entailment).

For example, if an ontology contains the information that Joe is married to Sam, that they are both employees of NewCo, and that only persons of opposite gender can be married, then we can return NewCo in response to a query for companies with both male and female employees, even if we don't know the gender of either Sam or Joe--this is because in all interpretations where Sam is male, Joe must be female, and vice versa. On the other hand, we may not be able to return NewCo in response to a query for companies with at least two employees, as our ontology may not rule out interpretations in which people are both male and female at the same time, where people can be married to themselves and where Joe and Sam could be two names for the same person.²

3.2 The Datalog Paradigm

The relational model underlying databases also models the domain in terms of objects and relationships³ between them, but makes several simplifying assumptions. In particular, it is assumed that the only objects and relationships that exist in the domain are those that are explicitly represented in the database (the closed world assumption), and that names uniquely identify objects in the domain, i.e., it is not the case that two different names identify the same object (the unique name assumption). The result of these assumptions is that there is a single (canonical) model, where objects and relationships are in a one to one correspondence with the data in the database. Given this close correspondence, it is often convenient to think of the data and the model as being the same thing.

In the database setting, query answering only requires checking the structure of this single model (i.e., of the database itself). While this is much easier (requiring time polynomial in the size of the data) than computing entailment with respect to an ontology (usually at least PSpace-complete in the size of the data), a single model is not able to capture situations like the NewCo one above: it would, e.g., be necessary to state the gender of persons and/or be assumed that any person not known to be male must be female.

Datalog is a formalisation of the database approach in which Horn-like rules are used to capture both the schema (i.e., structural constraints on the data) and the data itself. For example, the rule

$\syntax{Person}(y) \leftarrow \syntax{Person}(x) \land \syntax{parent}(x,y)$,

(recall that italics, e.g., $x$ and $y$, is used for variables) can be read as stating that, for any $x$ and $y$, if $x$ is a person, and $y$ is the parent of $x$, then $y$ is also a person. The antecedent ( $\syntax{Person}(x) \land \syntax{parent}(x,y)$ in this case) is often called the body of the rule, and the consequent ( $\syntax{Person}(y)$ in this case) is often called the head of the rule.

A rule with an empty head is often called a constraint,⁴ and is used to express the fact that interpretations satisfying the condition described in the body of the rule are not admitted. For example, the rule

$\mbox{}\leftarrow \syntax{Person}(x) \land \syntax{parent}(x,x)$

can be read as stating that no person can be their own parent.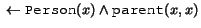

Finally, rules with empty bodies are used to capture data (often called ground facts). For example, the rule

$\syntax{married}(\syntax{Joe},\syntax{Sam}) \leftarrow$

can be read as stating that Joe is married to Sam.

It is normal to restrict rules to be safe. A safe rule is one where all of the variables in the head of a rule also occur in (positive atoms in) the body of the rule. For example, the rule

$\syntax{mother}(x,y) \leftarrow \syntax{Person}(x)$

(whose intended meaning is that every person has a mother) is unsafe, because the variable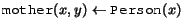 $y$ in the head of the rule does not occur in the body of the rule.

The semantics of Datalog relies on minimal Herbrand models: essentially, interpretations where the objects and relationships are limited to those mentioned in rules, and the only facts are those that are implied by the rules (i.e., the closed world assumption). When combined with the unique name assumption, this means that a collection of Datalog rules (sometimes called a Datalog program) still admits (at most) only one interpretation, and so has similar characteristics to a database: query answering is relatively easy (polynomial), but only relatively simple situations can be modelled, i.e., situations in which complete information is available. Datalog cannot, for example, be used to capture information such as the fact that all persons are either male or female, or the fact that all persons have exactly two parents.

Datalog can be extended in a variety of directions, e.g., with default negation (in the body of rules) and disjunction (in the head of rules).⁵ Such extensions are often indicated using superscripted operators, e.g., $\mbox{Datalog}^{\neg\lor}$ for Datalog with default negation and disjunction. For expressive extensions such as $\mbox{Datalog}^{\neg\lor}$ there may no longer be a single minimal interpretation. In this case the most commonly adopted semantics is to restrict attention to so-called ``stable models'' [18], i.e., interpretations where the interpretation of negated terms is fixed such that they are consistent with the rules.

For $\mbox{Datalog}^{\neg\lor}$, query answering is no longer so easy (co-NP-complete in the general case), but it is possible to model some kinds of incomplete information, e.g., the fact that all persons are either male or female. It is still not possible, however, to capture the fact that all persons have exactly two parents. Other reasoning tasks in $\mbox{Datalog}^{\neg\lor}$, including many reasoning tasks useful when working with ontologies (such as checking if it is possible for the ontology to have any interpretation), are even harder, NEXPTIME$^{\mbox{NP}}$-complete in the general case [13]. In fact, reasoning in the Description Logic can be reduced to reasoning in $\mbox{Datalog}^{\lor}$ [22]).

4 Conceptual Modelling in the Semantic Web

The differences between the Classical and Datalog paradigms have important consequences for modelling. The Datalog paradigm is, not surprisingly, well suited to closed and highly structured environments such as databases, where it is reasonable to assume that all relevant information is available. The Classical paradigm may have advantages, however, in an open and loosely structured environment such as the Semantic Web. In the following sections we will compare and contrast various aspects of the two paradigms, with particular reference to the kinds of situation that we can expect to arise in the Semantic Web.

4.1 Identifiers

An identifer is a name that is used to reference an individual (or property or class). Identifiers are not exactly part of the domain being modelled, instead providing a vocabulary of names that can be used to describe and refer to various aspects of the domain. They also provide a simple mechanism for establishing common references between different sources of information. One of the strengths of the Semantic Web is that it provides a nicely structured collection of identifiers in the form of IRI references.

As we saw in Section 3.2, the Datalog paradigm (along with many other representation formalisms) requires that different identifiers reference distinct individuals (the unique name assumption). That is, the person referenced via the identifier John_Smith is different from the person referenced via the identifier Bill_Jones.

The Semantic Web is a very hostile environment for the unique name assumption. There are many and varied sources of information in the Semantic Web, even in the same area, and these sources are free to coin their own identifiers (IRIs) for anything they choose. For example, there are many providers of FOAF information, each of which may choose to use different identifiers to identify to the same individuals. One such information source may use one identifier to identify a particular person, as in

$\syntax{mbox}(\syntax{http:/ex1.org/John\_Smith},\         \syntax{''\url{mailto:John_Smith@ex.com}''})$⁶

while another may use a different identifier for the same person, as in

$\syntax{mbox}(\syntax{http:/ex2.org/Jack\_Smith},\         \syntax{''\url{mailto:John_Smith@ex.com}''})$

Assuming that these two identifiers necessarily reference different individuals precludes the possibility that they may simply be two different ``names'' for the same individual.

In this sort of situation it is possible, and useful, to provide descriptions of situations in which two identifiers can be recognised as referencing the same individual. This is done in FOAF, where the mbox⁷ property is defined as an inverse functional property, which means that if two names are linked via $\syntax{mbox}$ to the same mailbox, then these two names must reference the same individual. (This is a slightly suspect modelling decision, as mailboxes are do not always uniquely identify people, so not all mailboxes can be used as FOAF mboxes.) The above two information sources would be inconsistent in FOAF if the unique name assumption were in force, but are not inconsistent without it; without the unique name assumption it would simply follow that $\syntax{http:/ex1.org/John\_Smith}$ and $\syntax{http:/ex2.org/Jack\_Smith}$ are two names for the same person.

Further, FOAF information sources need not provide any identifier for the people their information describes, instead only providing other uniquely identifying information (such as the name of their $\syntax{mbox}$), as in

$\syntax{mbox}(j,\syntax{''\url{mailto:John_Smith@ex.com}''})$

The use of such anonymous individuals does not fit well with the unique name assumption. Either each such individual is assumed to be different, which would clearly not be the intention if they have the same identifying information, or it must be possible for multiple anonymous references to identify a single individual, in which case the Datalog assumptions must be overturned, resulting in a different formalism and potentially losing the complexity benefits of Datalog.

This is not to say that it is not convenient to have a unique name assumption in many situations, such as names of seats on an airplane. As another example, it is the case in many settings that a single information source will indeed use different identifiers to identify distinct individuals. Here, the unique name assumption is a useful shortcut for a potentially large number of statements such as

$\syntax{John\_Smith} \neq \syntax{Bill\_Smith}$
$\syntax{John\_Smith} \neq \syntax{Susan\_Jones}$
$\syntax{Bill\_Smith} \neq \syntax{Susan\_Jones}$
...

that are required in the Classical paradigm in order to capture situations where different names necessarily identify distinct individuals.

The point remains, however, that in the Classical paradigm, although there is no assumption that different names identify different objects, it is possible to express the fact that a given set of names has this property. In the Datalog paradigm, on the other hand, different names always identify different objects.

4.2 Open World

The Semantic Web is a very open environment. In the Semantic Web there is no requirement that information sources be comprehensive in any way, or even that a collection of information sources be comprehensive. In such a setting it is often incorrect to assume that lack of information is equivalent to negative information, as in assuming that a person mentioned at some FOAF site knows no other person simply because there are no knows relationships for that person listed at the site. Further, even if the person has his or her own FOAF page that lists some of the people that they know, it is not necessarily the case that all of the people that they know are listed there. For example, if

$\syntax{knows}(\syntax{John\_Smith},\syntax{Bill\_Jones})$
$\syntax{knows}(\syntax{John\_Smith},\syntax{William\_Jones})$
$\syntax{Bill\_Jones} \neq \syntax{William\_Jones}$

are the only knows relationships found in (even) the web page of John_Smith, it is not appropriate to infer that John_Smith knows only two other people.

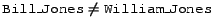
The Classical paradigm directly matches this important characteristic of the Semantic Web: it does not rule out interpretations in which John_Smith knows other people. On the other hand, the closed world assumption of the Datalog paradigm admits only one interpretation of the above information, an interpretation in which John_Smith knows exactly two other people.

It is possible to approximate some of the closed world behaviour of the Datalog paradigm in the unmodified Classical paradigm by appropriately interpreting the results of queries. For example, a query that asks for the people that John_Smith knows will return William_Jones and Bill_Jones. These two results for the query are the only ones sanctioned by the Classical paradigm. It is possible, then, to say in the Classical paradigm that there are only two people known to be known by John_Smith. This epistemic treatment of queries (asking about what is known) then mirrors the Datalog paradigm, where information that is not known is considered to be false. Query languages for open Semantic Web languages, e.g., SPARQL (http:/www.w3.org/TR/rdf-sparql-query/), can be profitably treated in this way.

This is not to say that it is not useful to be able to state or even infer comprehensive information. In most cases, however, this closure of information should be explicitly stated as an addition to the positive information. It is quite possible to ``close'' information in the Classical paradigm, for example by adding

$\syntax{John\_Smith} \in \atmost{2}{\syntax{knows}}$

to the above example.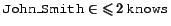

Situations where this kind of closure is appropriate are, however, mainly limited to database-like applications, such as a database of flight information, where it is reasonable to assume that all reservations for a flight are listed in the information source for that flight. The Datalog paradigm does do better in this sort of situation, as it can be very clumsy to state this sort of closed world assumption in the Classical paradigm. However, the Datalog paradigm achieves this benefit at the cost of making the closed world assumption everywhere.

4.3 Incomplete Information

In an open environment such as the Semantic Web, it is also important to allow other kinds of incomplete information besides the kind of incompleteness that comes from the open world assumption.

For example, it is useful to be able to state something about the people that John_Smith knows without providing complete information about them, or even saying who they are. We might like to say that John_Smith knows (at least) two other people without having to identify them. This is easy in the Classical paradigm, using a statement such as

$\syntax{John\_Smith} \in \atleast{2}{\syntax{knows}}$,

but it is not possible in the strict Datalog paradigm, where it is required that relationships be between particular named individuals.

One might imagine that it would be possible to express this sort of information in a Datalog setting by introducing two new individuals and stating that they are known by John_Smith. Due to the unique name assumption, however, these two individuals would be in addition to any other individuals that are known to John_Smith, and could lead to incorrect inferences about the total number of people that he knows; they would also lead to an incorrect answer to a query asking for all of the people that John_Smith knows.

A similar problem exists with respect to required information for classes. If we want every person to have both a gender and a birthplace, then the Classical paradigm does not require us to be able to identify the gender or birthplace of any given person. We can simply state, for example, that every Person has exactly one birthplace, which must be a Location, as in

$\syntax{Person} \Issub \exactly{1}{\syntax{birthplace}}$
$\syntax{Person} \Issub \all{\syntax{birthplace}}{\syntax{Location}}$.

It is then perfectly acceptable for there to be instances of Person whose birthplace is not known, for example

$\syntax{Person}(\syntax{John\_Smith})$.

This does not work in the Datalog paradigm in for two reasons. First, it is not possible to even state that every Person has a birthplace, because a rule expressing this, e.g.,

$\syntax{birthplace}(x,y) \leftarrow \syntax{Person}(x)$,

would not be a safe rule.

Even if unsafe rules where to be allowed in a way that preserves the computational properties of Datalog, the closed world assumption of the Datalog paradigm causes this rule to have a different effect. Instead of requiring every Person to have a birthplace, it requires that every Person has a known birthplace. (For more on this sort of reading for rules, see the discussion of restrictions versus constraints in the next section.)

Again, the difference between the Classical and Datalog paradigms is that the Classical paradigm is more flexible: in the Datalog paradigm, information must be complete, whereas in the Classical paradigm, information may be incomplete, but particular information can be made complete if desired.

4.4 Restrictions vs Constraints

The Classical paradigm admits that there can be many different states of affairs (interpretations), and only requires that each of these interpretations is consistent with the statements (axioms) that have been made. Adding new information means placing additional requirements on interpretations, which may rule out some interpretations that had previously been consistent.

In the Datalog paradigm, on the other hand, there is (at most) one state of affairs, which corresponds to the explicitly asserted data augmented with data derived via application of the (non-constraint) rules. Adding new non-constraint rules does not restrict the possible states of affairs, but instead augments the inferred information. Limiting the possible states of affairs cannot thus be done directly in the Datalog paradigm. Instead constraint rules⁸ can be used to make certain inputs illegal.

This difference can be easily seen when providing local ranges for properties. For example,

$\syntax{Person} \Issub \all{\syntax{knows}}{\syntax{Person}}$

is the way to state, in the Classical paradigm, that Persons know only other Persons. The corresponding constraint rule in the Datalog paradigm is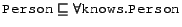

$$\begin{array}{l} \leftarrow \syntax{Person}(x) \land \syntax{knows}(x,y) \land \neg \syntax{Person}(y) \end{array}$$ (1)

The effects of these two approaches is quite different. In the Classical paradigm it is perfectly fine to state a knows relationship, such as

$\syntax{knows}(\syntax{John\_Smith},\syntax{Fred\_Smith})$

without also stating (or otherwise being able to infer) that Fred_Smith is a Person. Because the local range axiom restricts possible states of affairs to be those where all parents are people, Fred_Smith will be inferred to be a Person. In the Datalog paradigm, on the other hand, the constraint rule makes the above statement, by itself, illegal.

The Datalog paradigm also allows for non-constraint rules that mirror Classical restrictions. The restriction above can, for example, be modelled using the rule

$$\begin{array}{l} \syntax{Person}(y) \leftarrow \syntax{Person}(x) \land \syntax{knows}(x,y) \end{array}$$ (2)

Such rules can, however, only augment information about known individuals, as the Datalog paradigm does not allow for the existence of individuals whose name is not known (see Section 4.4.3).

4.4.1 Value Restrictions vs Value Constraints

As the Semantic Web is an open environment, information can come from a variety of different sources. For example, a FOAF ontology may provide the class Person and property parent, further requiring that all parents of instances of Person also be instances of Person, as in

$$\begin{array}{l} \syntax{Person} \Issub \all{\syntax{parent}}{\syntax{Person}} \end{array}$$ (3)

Another ontology may extend this FOAF ontology by adding the class Adult, and further requiring that all parents of people are instances of the Adult class, as in

$$\begin{array}{l} \syntax{Person} \Issub \all{\syntax{parent}}{\syntax{Adult}} \end{array}$$ (4)

In the Classical paradigm, information sources written for the first ontology, such as

$$\begin{array}{l} \syntax{Person}(\syntax{John\_Smith}) \ \... ...{parent}(\syntax{John\_Smith},\syntax{Fred\_Smith}) \end{array}$$ (5)

can be used in the second ontology, because their use in the second ontology will simply result in additional inferences based on the additional restrictions provided by the second ontology. In the above case, for example, an additional inference would be

$\syntax{Adult}(\syntax{Fred\_Smith})$.

Using Datalog constraints, on the other hand, severely limits the ability to combine information sources. For example, the constraint version of axiom (3) would be the constraint rule

$$\begin{array}{l} \leftarrow \syntax{parent}(x,y) \land \neg \syntax{Person}(y) \end{array}$$ (6)

which states that it is ``illegal'' for any individual to be a parent without also being a Person. Note that, because of the closed world assumption, any individual that is not provably a Person is taken not to be a person, so the information given in axiom (5) above would not lead to the inference that Fred_Smith must be a Person, but would instead be treated as ``illegal'' (because it violates the constraint). Any valid information source would, therefore, have to include the information that Fred_Smith is a Person, e.g.,

$$\begin{array}{l} \syntax{Person}(\syntax{John\_Smith}) \ \... ...parent}(\syntax{John\_Smith},\syntax{Fred\_Smith}). \end{array}$$ (7)

This is not too onerous a burden if the information source is written with the first ontology/constraint in mind, and even, as de Bruijn et al [7] claim, has some modelling benefits having to do with lack of surprises.⁹

However, the constraint methodology breaks down in the common-to-the-Semantic-Web presence of extended ontologies such as the one that includes axiom (4) above, which would be rendered in the constraint modelling methodology as

$$\leftarrow \syntax{parent}(x,y) \land \neg \syntax{Adult}(y)$$ (8)

Even the extended information source (7) above would not be valid in this extended ontology, because it does not include the required information that Fred_Smith is an Adult.

Avoiding this problem by utilizing the non-constraint rules is not an effective solution. The presence of a non-constraint rule like rule (2) results in all parents being inferred to belong to Person, so the constraint rule (6) will never be violated and thus is useless. The constraints modelling methodology thus seems to be in conflict with the open nature of the Semantic Web, which encourages the sharing, reuse and extension of information.

Such constraints also introduce a limited form of non-monotonicity. As we have seen above, for example, the augmented information source (7) above is inconsistent with respect to the extended ontology including the constraint (8). If

$\syntax{Adult}(\syntax{Fred\_Smith})$

is added, however, there is no longer any inconsistency.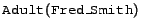

4.4.2 Cardinality Restrictions vs Cardinality Constraints

In the Classical paradigm, cardinality restrictions are an important way of inferring that two identifiers identify (i.e., are different names for) the same individual. This sort of inference is particularly important in the Semantic Web, where different sources may use different identifiers for the same individual.

As mentioned above, FOAF mailboxes form a unique identifier for members of Person (i.e., mbox is an inverse functional property in FOAF). So, if one information source includes

$\syntax{mbox}(\syntax{Bill\_Jones},\         \syntax{''\url{mailto:Bill_Jones@ex.com}''})$

and another includes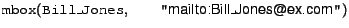

$\syntax{mbox}(\syntax{William\_Jones},\         \syntax{''\url{mailto:Bill_Jones@ex.com}''})$,

then it can be inferred from the two sources that Bill_Jones and William_Jones identify the same individual. This is not possible in the Datalog paradigm, as the two different identifiers would necessarily identify different individuals, leading to a contradiction.

Of course, this power does have its dangers. Consider the airline flight example from de Bruijn et al [7] (slightly modified)

$\syntax{FlightSeat} \Issub \atmost{1}{\syntax{hasPassenger}}$
$\syntax{FlightSeat}(\syntax{seat1})$
$\syntax{hasPassenger}(\syntax{seat1},\syntax{mary})$
$\syntax{hasPassenger}(\syntax{seat1},\syntax{john})$.

This is not a contradiction, as mary and john could be the same, and due to the cardinality restriction it is inferred that they are, indeed, the same.

This may not be the intent of the modeler. However, if it is not the intent, then there is an easy solution--simply state that these two individuals are different, as in

$\syntax{mary} \neq \syntax{john}$.

With the addition of this information, the above example does produce the desired contradiction. Not only does this solve the possible problem here, it is also a good idea in general to explicate inequalities (and disjointness) where they are known.

4.4.3 Existential Restrictions vs Existential Constraints

Other common situations cause even more problems when rendered as constraints. For example, consider trying to model how a mother property should work, i.e., that every element of Person has exactly one mother, who is also a Person. In the Classical paradigm this is quite easy, for example by using the axioms

$\syntax{Person} \Issub \exactly{1}{\syntax{mother}}$
$\syntax{Person} \Issub \all{\syntax{mother}}{\syntax{Person}}$.

This ensures that mother has the desired characteristics, and allows for situations where the mother of a Person is known, as in

$\syntax{mother}(\syntax{John\_Smith},\syntax{Mary\_Smith})$,

as well as situations where little or nothing is known about the mother of a given Person, as in

$\syntax{Person}(\syntax{John\_Smith})$.

In the Datalog paradigm, this sort situation is extremely problematic. Rendering it in restriction-like rules results in unsafe rules such as

$\syntax{mother}(x,y) \leftarrow \syntax{Person}(x)$,

which are not allowed in the Datalog paradigm. Rendering it as constraints, as in

$\leftarrow \syntax{Person}(x) \land \neg \syntax{mother}(x,y)$
$\leftarrow \syntax{Person}(x) \land \syntax{mother}(x,y) \land \neg \syntax{Person}(y)$

looks better initially, or at least fits within the Datalog paradigm.

It is not possible, however, to use this reasonable-looking pair of rules. Consider any instance of Person in this information source. This individual has to have a known mother, who has to be a Person as well, and so on. This means that the information source either has to include an infinite chain of mother links and an infinite number of Persons, which is obviously not possible, or there has to be a loop in the mother links (i.e., some person whose mother is one of their own descendants), which clearly conflicts with the desired meaning.¹⁰

4.5 Datatypes

It is, of course, vital to have a treatment of what are generally called datatypes in a Semantic Web modelling language. This has been provided in RDF and OWL by utilizing certain datatypes from XML Schema, including strings and integers.

This is perfectly consistent with the Classical paradigm. In the Classical paradigm, datatypes are treated in the same way as classes, and datatype values are treated in the same way as individual identifiers (i.e., a data value is treated as referring to an object).¹¹Much more is known, however, about the possible interpretation of datatypes, data values and relationships between them, i.e., there are built in restrictions on possible states of affairs where they relate to the interpretation of data types and values. For example, it is known that the integer values ``1'' and ``2'' cannot identify the same object, and that the objects that these two values identify must be in a ``$<$'' relationship. It is possible, however, that two different data values are interpreted as the same object, e.g., the decimal values ``1'' and ``1.0''.

All this behaviour can be built in to a formalism, like RDF or OWL, that belongs to the Classical paradigm. As much more is known about possible interpretations of datatype domains, however, it is much more likely that non-trivial inferences will cause a conflict (i.e., be incompatible with any possible interpretation), but this is only to be expected. For example, if our information source includes

$\syntax{hasAge}(\syntax{Bill\_Jones},35)$
$\syntax{hasAge}(\syntax{William\_Jones},46)$,

where hasAge is a functional datatype property, then inferring that Bill_Jones and William_Jones identify the same person will lead to a contradiction.

Neither is there much about datatypes that goes against the Datalog paradigm. The Datalog models are just suitably augmented with domain elements corresponding to the datatype values and the syntactical values are mapped into these domain elements. Care does have to be taken with different syntactical values that map into the same domain element, but this is not a significant concern.

4.6 The Role of Tools

Finally, it should be noted that there is indeed a preference amongst users for the Datalog paradigm in some areas. In some domains it may be easier to start modelling using the Datalog paradigm--provided that the domain can be modelled in the Datalog paradigm at all--as the Classical paradigm requires more specification (e.g., stating that certain names denote distinct individuals, providing local closed world information, etc.).

Ontology-building tools with good user interfaces can help here. For example, it is not difficult to generate the statements required to explicitly state the unique name assumption for a group of identifiers. In a good tool it would not even be necessary to pick out the relevant identifiers: it would be sufficient to state that, in the information source being constructed, the identifiers referring to instances of a particular class all identify distinct individuals. The tool can then generate the required inequality axioms.

Good user interfaces can also help in determining the appropriate information to add to provide closure information, such as determining that

$\syntax{John\_Smith} \in \atmost{2}{\syntax{knows}}$

would provide local closure for the people that John_Smith knows. They can also be used to point out potential ``surprises'' resulting from the inferences performed in the Classical paradigm, such as the ones mentioned by de Bruijn et al [7], thus suggesting improvements to the deficient ontology or other information source. In fact state-of-the-art ontology editing tools such as Protégé [24] and Swoop [23] already include explanation facilities that help users to pinpoint the cause of unexpected inferences.

5 Reasoning in the Semantic Web

5.1 Complexity

At first glance, the Datalog paradigm seems to offer significant advantages with respect to the complexity of reasoning. Reasoning in the Classical paradigm is difficult for any reasonably expressive ontology language. For example, reasoning in the OWL DL Web Ontology Language is NEXPTIME-complete [21].

The polynomial-time reasoning result for Datalog looks very attractive when compared to this difficult reasoning in the Classical paradigm. However, the caveats associated with the result make it much less attractive than might first be imagined. One of these caveats is that the result only applies to standard query answering, i.e., queries about individuals, against a fixed program--as soon as changes to the program are allowed, then complexity becomes exponential (in fact EXPTIME-complete). The polynomial-time complexity result does not, therefore, apply to many interesting schema level queries, as reductions to standard query answering (e.g., for subclass queries) require changing the program in the general case.

The polynomial-time reasoning results also do not hold for the more expressive versions of Datalog such as $\mbox{Datalog}^{\neg\lor}$. Unrestricted use of negation as failure, for example, pushes even query answering beyond polynomial time, and full reasoning in this version of Datalog is NEXPTIME$^{\mbox{NP}}$-complete [13]. As mentioned earlier, reasoning in the Description Logic can be reduced to reasoning in $\mbox{Datalog}^{\lor}$ [22].

5.2 Inferencing

As discussed in Section 4, one of the attractive characteristics of the Classical paradigm is the inferencing that it supports. For example, the large Semantic Web namespace means that different information sources may use different names for the same individuals, and thus inferring equality is a useful inference. The unique name assumption of the Datalog paradigm prevents this kind of inference, whereas the Classical paradigm can easily support it.¹² Moreover, information to the effect that different identifiers reference different individuals does not affect complexity in the Classical paradigm; reasoning gets no harder computationally as more identifiers are known to reference different individuals and often becomes easier in practice.

Even the basic formulations of class-level inference (such as identifying instance and subclass relationships) are suspect in the Datalog paradigm. What does it mean to ask whether a class defined using constraints is a subclass of another class, or if an individual is an instance of such a class? It is not correct to assume that constraints have no consequences. For example,

$\leftarrow \syntax{Person}(x) \land \syntax{child}(x,y) \land \neg \syntax{Person}(y)$
$\syntax{Person}(\syntax{John\_Smith})$

implies both

$\syntax{Person} \sqsubseteq \all{\syntax{child}}{\syntax{Person}}$

and

$\syntax{John\_Smith} \in \all{\syntax{child}}{\syntax{Person}}$,

but accounts that use the Datalog paradigm to build ontology formalisms, such as OWL Flight [7], do not provide coherent accounts of how to determine such relationships.

6 The Way Ahead

As we have seen, the open world semantics of the Classical paradigm is generally quite a good match to the openness of the Semantic Web, but there may be situations in which it would be convenient to apply a local closed world and/or unique name assumption, for example when accessing comprehensive information sources such as flight schedules. There are several possible ways in which this might be achieved.

6.1 Using Queries

As discussed in Section 4.2, the epistemic semantics of queries gives them a closed world flavour, even in a Classical setting. For example, a query asking for cities with a direct British Airways flight to London will return only those cities known to have such a flight. If it is believed that a source of information, such as the British Airways online schedule, is fully comprehensive, then an application can use (possibly multiple) queries to provide useful kinds of closed world behaviour. For example, retrieving European Union capitals not having such a flight could be achieved by subtracting the answer to the above query from the answer to a query for European capitals. Many query languages, including SQL and SPARQL, have a built in algebra for performing this kind of manipulation on query answers.

6.2 Integrating DL and Rules

There have been many proposals for integrating Classical ontology languages, in particular description logics, with Datalog style rules languages [9,25,29,15,32]. The general idea is that the rules can use unary and binary predicates from the ontology (i.e., classes and properties) as well as predicates that occur only in rules (rules predicates). In order to maintain the decidability of the integrated language, there is usually a ``safety'' condition that restricts variables occurring in the head of a rule to those that occur in at least one positive rules predicate in the body of the rule.

The safety condition means that, in effect, rules can only apply to named individuals. From a certain perspective the rules can, therefore, be seen as providing a powerful query language. For example, if we assume that EU-cap is the class of European Union capitals and BA-flight is a rules predicate that is true for all pairs of cities connected by a direct British Airways flight, then the rule

$\syntax{IsolatedCap}(x) \leftarrow \            \syntax{EU-cap}(x) \land \neg\syntax{BA-flight}(x,\syntax{London})$

would state that European Union capitals not having a direct British Airways flight to London are instances of IsolatedCap.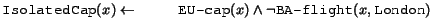

There have also been proposals for integrating more powerful rules languages, in particular Answer Set Programming languages, with description logics [14]. This approach is, however, less well understood, requires a more esoteric semantics for the integrated language and introduces significant computational complexity (e.g., the complexity of standard reasoning tasks becomes, in the general case, NP $^{\mbox{NEXP}}$-complete).

6.3 Extending the Classical Paradigm

Another way in which to apply a local closed world and/or unique name assumption would be to augment the Classical paradigm with constructs that could provide a Datalog-like flavour for portions of the Semantic Web. For example, there is no conceptual problem in providing constructs that state that certain information sources abide by the unique name assumption or are complete in some way. There have, indeed, been proposals to add such constructs to Description Logics [2]. The unrestricted use of these constructs does increase the difficulty of reasoning, but if they are limited to database-like sources, then no extra computational load is generated.

A particularly interesting and general way of adding closed-world constructs is to use epistemic operators in the style of Lifshitz [26]. One of the nicest aspects of Lifshitz's work is that it can be given a clean model theoretic semantics in the style of the model theoretic semantics for RDF and OWL.

The epistemic operators in the logic allow one to access the entirely of the knowledge expressed in a knowledge base. For example, constraint rule 1 is expressed epistemically as

$\forall x,y \; \ensuremath{\mathbf K}\xspace \syntax{Person}(x) \land \ensurema... ...) \            \rightarrow \ensuremath{\mathbf A}\xspace \syntax{Person}(y)$

The and operators provide a clean way to access internal knowledge. The operator can be read something like ``the system knows'', and the operator can be read here something like ``the system already knows''.

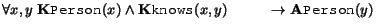
Considerable work has already been done on the addition of epistemic constructs to Description Logics, and much of this work could be carried over into the Semantic Web, in particular as extensions to OWL DL. Early work by Donini et al [10] added the operator to the Description Logic . Limiting where this operator can be placed results in an epistemic description logic that can express much closed world information, including closure of database-like information, without increasing the computational complexity of the logic.

Later work by Donini et al [11,12] included also the nonmonotonic epistemic operator, , again in the style of Lifshitz. This extended logic is very powerful, and can express very many different kinds of defaults as well as procedural rules, integrity constraints, and closure. Reasoning in this epistemic description logic is, however, harder than in a description logic without the epistemic operators.

7 Discussion

We see two very different ways of modelling the world. At one extreme there is the Classical paradigm, where unstated information is left open. At the other extreme there is the Datalog paradigm, where unstated information is assumed to be false. The Datalog paradigm has some allure, particularly as it is closer to the common database view, but we argue that this closed view is not very compatible with the Semantic Web.

We argue that the Classical paradigm is better for modelling in the (open) Semantic Web than the Datalog paradigm. We do admit that the Classical paradigm has some pitfalls for those used to database modelling, but we believe that most of these can be easily handled with the help of good ontology building tools, which can be used to generate much of the extra information needed for the Classical paradigm. We also admit that the openness of the Classical paradigm can result in additional computational requirements, at least in some areas.

Good modelling requires considerable (fore)thought in any context. The open and distributed nature of the Semantic Web does not make modelling any easier; on the contrary, modelling in the Semantic Web is more difficult than modelling in, for example, a database setting. Pushing the Semantic Web back towards a closed paradigm, however, would negate much of the power of the Semantic Web.

A promising direction for the future is to add epistemic constructs to OWL. An epistemic Description Logic provides a formalism that is mostly open, but that can close certain areas of information as desired. Much work remains to be done here, particularly to identify useful subsets in which reasoning can be performed effectively (much as regular Description Logics identify such subsets of first-order logic), but the result could be a logic that combines most of the advantages of the Classical and Datalog paradigms.

To be able to utilize such logics, however, the lower levels of the Semantic Web cannot be hostile to openness. We thus believe that the best foundational paradigm for the Semantic Web is the Classical paradigm with its inherent openness. Extensions can then limit this openness where required. The Datalog paradigm, on the other hand, is inherently closed, and it is not amenable to being opened.

Bibliography

1

R. Agrawal and N. H. Gehani.
Ode (object database and environment): The language and the data model.
In Proceedings of the 1989 ACM SIGMOD International Conference on Mangement of Data, pages 36-45. Association for Computing Machinery, June 1989.

2

F. Baader, D. Calvanese, D. L. McGuinness, D. Nardi, and P. F. Patel-Schneider, editors.
The Description Logic Handbook: Theory, implementation, and applications.
Cambridge University Press, 2003.

3

T. Berners-Lee.
Semantic web road map, Sept. 1998.
Available at http:/www.w3.org/DesignIssues/Semantic.html.

4

T. Berners-Lee, J. Hendler, and O. Lassila.
The semantic Web.
Scientific American, 284(5):34-43, 2001.

5

D. Brinkley and R. V. Guha.
RDF vocabulary description language 1.0: RDF schema.
W3C Recommendation, http:/www.w3.org/TR/rdf-schema, 2004.

6

J. de Bruijn, A. Polleres, R. Lara, and D. Fensel.
OWL Flight.
Working Draft D20.3 v0.1, WSML, 23 August 2004.
Available at http:/www.wsmo.org/2004/d20/d20.3/v0.1/.

7

J. de Bruijn, A. Polleres, R. Lara, and D. Fensel.
OWL DL vs. OWL Flight: Conceptual modeling and reasoning for the semantic web.
In Proceedings of the 14th World Wide Web Conference, Japan, May 2005.

8

M. Dean, G. Schreiber, S. Bechhofer, F. van Harmelen, J. Hendler, I. Horrocks, D. L. McGuinness, P. F. Patel-Schneider, and L. A. Stein.
OWL web ontology language: Reference.
W3C Recommendation, http:/www.w3.org/TR/owl-ref/, 2004.

9

F. M. Donini, M. Lenzerini, D. Nardi, and A. Schaerf.
AL-log: Integrating datalog and description logics.
Journal of Intelligent Information Systems, 10(3):227-252, 1998.

10

F. M. Donini, M. Lenzerini, D. Nardi, A. Schaerf, and W. Nutt.
Adding epistemic operators to concept languages.
In B. Nebel, C. Rich, and W. Swartout, editors, Principles of Knowledge Representation and Reasoning: Proceedings of the Third International Conference (KR'92), pages 342-353. Morgan Kaufmann Publishers, San Francisco, California, Oct. 1992.

11

F. M. Donini, D. Nardi, and R. Rosati.
Autoepistemic description logics.
In Proceedings of the Fifteenth International Joint Conference on Artificial Intelligence, pages 136-141. International Joint Committee on Artificial Intelligence, Aug. 1997.

12

F. M. Donini, D. Nardi, and R. Rosati.
Description logics of minimal knowledge and negation as failure.
ACM Transactions on Computational Logic, 3(2):177-255, 2002.

13

T. Eiter, G. Gottlob, and H. Mannilla.
Disjunctive datalog.
ACM Transactions on Database Systems, 22(3):364-418, 1997.

14

T. Eiter, T. Lukasiewicz, R. Schindlauer, and H. Tompits.
Combining answer set programming with description logics for the semantic web.
In Principles of Knowledge Representation and Reasoning: Proceedings of the Ninth International Conference (KR2004), pages 141-151, June 2004.

15

E. Franconi and S. Tessaris.
Rules and queries with ontologies: A unified logical framework.
In H. J. Ohlbach and S. Schaffert, editors, Principles and Practice of Semantics Web Reasoning: Second International Workshop, number 3208 in Lecture Notes in Computer Science, pages 50-60. Springer-Verlag, Sept. 2004.

16

A. V. Gelder, K. Ross, and J. S. Schlipf.
The well-founded semantics for general logic programs.
Journal of the ACM, 38(3):620-650, 1991.

17

M. Gelfond and V. Lifschitz.
The stable model semantics for logic programming.
In R. A. Kowalski and K. Bowen, editors, Proceedings of the Fifth International Conference on Logic Programming, pages 1070-1080, Cambridge, Massachusetts, 1988. The MIT Press.

18

M. Gelfond and V. Lifschitz.
Classical negation in logic programs and disjunctive databases.
New Generation Computing, 9(3/4), 1991.

19

V. Haarslev and R. Möller.
Expressive ABox reasoning with number restrictions, role hierarchies, and transitively closed roles.
In A. G. Cohn, F. Giunchiglia, and B. Selman, editors, Principles of Knowledge Representation and Reasoning: Proceedings of the Seventh International Conference (KR2000), pages 273-284. Morgan Kaufmann Publishers, San Francisco, California, Apr. 2000.

20

P. Hayes.
RDF semantics.
W3C Recommendation, http:/www.w3.org/TR/rdf-mt/, 2004.

21

I. Horrocks and P. Patel-Schneider.
Reducing OWL entailment to description logic satisfiability.
Journal of Web Semantics, 1(4):345-357, 2004.

22

U. Hustadt, B. Motik, and U. Sattler.
Reducing SHIQ-description logic to disjunctive datalog programs.
In Principles of Knowledge Representation and Reasoning: Proceedings of the Ninth International Conference (KR2004), pages 152-162, June 2004.

23

A. Kalyanpur, B. Parsia, and J. Hendler.
A tool for working with web ontologies.
International Journal on Semantic Web and Information Systems, 1(1):36-49, 2005.

24

H. Knublauch, R. Fergerson, N. Noy, and M. Musen.
The Protégé OWL plugin: An open development environment for semantic web applications.
In S. A. McIlraith, D. Plexousakis, and F. van Harmelen, editors, Proceedings of the Third International Semantic Web Conference, number 3298 in Lecture Notes in Computer Science, pages 229-243. Springer, Nov. 2004.

25

A. Y. Levy and M.-C. Rousset.
CARIN: A representation language combining horn rules and description logics.
In W. Wahlster, editor, Proceedings of the 12th European Conference on Artificial Intelligence (ECAI'96), pages 323-327. John Wiley & Sons Ltd., 1996.

26

V. Lifschitz.
Nonmonotonic datatbases and epistemic queries.
In Proceedings of the Twelfth International Joint Conference on Artificial Intelligence, pages 381-386, Sydney, Australia, Aug. 1991. International Joint Committee on Artificial Intelligence.

27

J. W. Lloyd.
Foundations of Logic Programming (Second, Extended Edition).
Springer-Verlag, Berlin, Heidelberg, 1987.

28

F. Manola and E. Miller.
RDF primer.
W3C Recommendation, http:/www.w3.org/TR/rdf-primer/, 2004.

29

B. Motik, U. Sattler, and R. Studer.
Query answering for OWL-DL with rules.
In S. McIlraith, D. Plexousakis, and F. van Harmelen, editors, Proceedings of the Third International Semantic Web Conference, number 3298 in Lecture Notes in Computer Science, pages 549-563. Springer, Nov. 2004.

30

Resource description framework (RDF): Model and syntax specification.
W3C Recommendation, 22 February 1999, http:/www.w3.org/TR/1999/REC-rdf-syntax-19990222/, Feb. 1999.

31

P. F. Patel-Schneider, P. Hayes, and I. Horrocks.
OWL web ontology language: Semantics and abstract syntax.
W3C Recommendation, http:/www.w3.org/TR/owl-semantics/, 2004.

32

R. Rosati.
On the decidability and complexity of integrating ontologies and rules.
Journal of Web Semantics, 3, 2005.

33

J. D. Ullman.
Principles of Database and Knowledge-Base Systems.
Computer Science Press, 1988.

Footnotes

... information.¹

For more information about FOAF, see http:/www.foaf-project.org.

... person.²

Clearly, we might expect a ``good'' ontology to rule out some of these possibilities.

... relationships³

We use the neutral term ``relationship'' to signify semantic relationships between object in the model.

...constraint,⁴

We will use the terminology from the database literature, and call these sorts of constructs constraints. Other axiomatic restrictions on the structure of interpretations can, in general, also be called constraints, but we will restrict ourselves to using constraint in the database sense in order to emphasize the difference between the Datalog and Classical paradigms.

... rules).⁵

Allowing disjunction in the body of rules does not extend the expressive power of the language, as such a rule can simply be rewritten as multiple rules without disjunction [27].

... $\syntax{mbox}(\syntax{http:/ex1.org/John\_Smith},\         \syntax{''\url{mailto:John_Smith@ex.com}''})$⁶

This is the only place that we will use fully-written out IRI references for identifiers as they are very long and interrupt the page layout. We will also generally eschew the use of qualified names, instead assuming that the unqualified short names we use are shorthand for an appropriate fully-written out IRI reference.

...mbox⁷

Of course, we mean here the mailbox property defined in the FOAF ontology.

... rules⁸

Recall from Section 3.2 that a constraint in the Datalog paradigm is a rule with an empty head, whose meaning is that we do not admit models satisfying the conditions expressed in the body of the rule.

... surprises.⁹

De Bruijn et al [7] provide the following example (slightly modified) of a potentially surprising inference:

$\syntax{FlightSeat} \Issub \all{\syntax{hasPassenger}}{\syntax{Passenger}}$
$\syntax{FlightSeat}(\syntax{seat3})$
$\syntax{FlightSeat}(\syntax{seat2})$
$\syntax{hasPassenger}(\syntax{seat2},\syntax{seat3})$

There is no contradiction here; instead it is inferred that seat3 is a member of Passenger, which might not be what is wanted. The solution, of course, is to explicitly state the disjointness of Passenger and FlightSeat, in which case the above forms a contradiction, as was probably desired.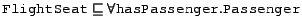

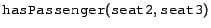
... meaning.¹⁰

The Classical model may not rule out such cyclical mother links, but it does not force all interpretations to include such cycles.

... object).¹¹

RDF and OWL DL do restrict where these values can appear in their syntax, but this does not affect their meaning.

... it.¹²

Certain systems, such as older versions of RACER [19], do have a unique name assumption built in, but the unique name assumption is certainly not a required part of the Classical paradigm.