To Randomize or Not To Randomize: Space Optimal Summaries for Hyperlink Analysis1

Tamás Sarlós, András A. Benczúr, Károly Csalogány

Computer and Automation Research Institute, Hungarian Academy of Sciences (MTA SZTAKI) and Eötvös University
Budapest, Hungary

Dániel Fogaras, Balázs Rácz

Computer and Automation Research Institute, Hungarian Academy of Sciences (MTA SZTAKI) and Budapest University of Technology and Economics
Budapest, Hungary

Copyright is held by the World Wide Web Conference Committee (IW3C2). Distribution of these papers is limited to classroom use, and personal use by others.
WWW 2006, May 23.26, 2006, Edinburgh, Scotland.
ACM 1-59593-323-9/06/0005.

ABSTRACT

Personalized PageRank expresses link-based page quality around user selected pages. The only previous personalized PageRank algorithm that can serve on-line queries for an unrestricted choice of pages on large graphs is our Monte Carlo algorithm [WAW 2004]. In this paper we achieve unrestricted personalization by combining rounding and randomized sketching techniques in the dynamic programming algorithm of Jeh and Widom [WWW 2003]. We evaluate the precision of approximation experimentally on large scale real-world data and find significant improvement over previous results. As a key theoretical contribution we show that our algorithms use an optimal amount of space by also improving earlier asymptotic worst-case lower bounds. Our lower bounds and algorithms apply to SimRank as well; of independent interest is the reduction of the SimRank computation to personalized PageRank.

Categories & Subject Descriptors

H.3.3 [Information Storage and Retrieval]: Information Search and Retrieval
G.2.2 [Discrete Mathematics]: Graph Theory - Graph algorithms
G.3 [Mathematics of Computing]: Probability and Statistics - Probabilistic algorithms

General Terms

Algorithms, Theory, Experimentation

Keywords

link-analysis, similarity search, scalability, data streams

1 Introduction

The idea of using hyperlink mining algorithms in Web search engines appears since the beginning of the success of Google's PageRank [24]. Hyperlink based methods are based on the assumption that a hyperlink $ u \to v$ implies that page $ u$ votes for $ v$ as a quality page. In this paper we address the computational issues [13,17,11,12] of personalized PageRank [24] and SimRank [16].

Personalized PageRank (PPR) [24] enters user preferences by assigning more importance to the neighborhood of pages at the user's selection. Jeh and Widom [16] introduced SimRank, the multi-step link-based similarity function with the recursive idea that two pages are similar if pointed to by similar pages. Notice that both measures are hard to compute over massive graphs: naive personalization would require on the fly power iteration over the entire graph for a user query; naive SimRank computation would require power iteration over all pairs of vertices.

We give algorithms with provable performance guarantees based on computation with sketches [7] as well as simple deterministic summaries; see Table 1 for a comparison of our methods with previous approaches. We may personalize to any single page from which arbitrary page set personalization follows by linearity [13]. Similarly, by our SimRank algorithm we may compute the similarity of any two pages or the similarity top list of any single page. Motivated by search engine applications, we give two-phase algorithms that first compute a compact database from which value or top list queries can be answered with a low number of accesses. Our key results are summarized as follows:

$ \bullet$
We give practical methods for serving unrestricted on-line personalized PageRank (Section 2.1) as well as SimRank queries with space a reasonable constant per vertex (Section 3). The methods are based on deterministic rounding.
$ \bullet$
We give a theoretically optimal algorithm for personalized PageRank value queries (Section 2.2) based on randomized sketching. Given an additive error $ \epsilon $ and the probability $ \delta $ of an incorrect result, we improve the disk usage bound from $ n\log n\log\left(1/\delta\right)/\epsilon^2$ [11,12] to $ n\log\left(1/\delta\right)/\epsilon$.
$ \bullet$
We give theoretically optimal algorithms for SimRank value and top list queries (Section 3.1) by a nontrivial reduction of SimRank to personalized PageRank.
$ \bullet$
We improve the communication complexity based lower
bounds of [11,12] for the size of the database (Section 4); our bounds are matched by our algorithms. Our sketch-based algorithms use optimal space; surprisingly for top list queries deterministic rounding is already optimal in itself.
$ \bullet$
In Section 5 we experimentally analyze the precision of approximation over the Stanford WebBase graph and conclude that our summaries provide better approximation for the top personalized PageRank scores than previous methods.


Table 1: Comparison of personalized PageRank algorithms for graphs of $ n$ vertices, additive error $ \epsilon $ and error probability $ \delta $.

\begin{table}%[ht!] \begin{tabularx}{\linewidth}{\vert p{2.6cm}\vert X\vert p{1... ...arx}$*$\ optimal for top queries \ $**$\ optimal for value queries \end{table}

1.1 Related Results

The scalable computation of personalized PageRank was addressed by several papers [13,18,17] that gradually increase the choice for personalization. By Haveliwala's method [13] we may personalize to the combination of 16 topics extracted from the Open Directory Project. The BlockRank algorithm of Kamvar et al. [18] speeds up personalization to the combination of hosts. The state of the art Hub Decomposition algorithm of Jeh and Widom [17] computed and encoded personalization vectors for approximately 100K personalization pages.

To the best of our knowledge, the only scalable personalized PageRank algorithm that supports the unrestricted choice of the teleportation vector is the Monte Carlo method of [11]. This algorithm samples the personalized PageRank distribution of each page simultaneously during the precomputation phase, and estimates the personalized PageRank scores from the samples at query time. The drawback of the sampling approach is that approximate scores are returned, where the error of approximation depends on the random choice. In addition the bounds involve the unknown variance, which can in theory be as large as $ \Omega(1)$, and hence we need $ \Theta({1 \over {\epsilon^2}}\log{1/\delta})$ random samples. Indeed a matching sampling complexity lower bound for telling binomial distributions with means $ 1/2\pm\epsilon$ apart [1] indicates that one can not reduce the number of samples when approximating personalized PageRank. Similar findings of the superiority of summarization or sketching over sampling is described in [5]. The algorithms presented in Section 2 outperform the Monte Carlo method by significantly reducing the error.

We also address the computational issues of SimRank, a link-based similarity function introduced by Jeh and Widom [16]. The power iteration SimRank algorithm of [16] is not scalable since it iterates on a quadratic number of values, one for each pair of Web pages; in [16] experiments on graphs with no more than 300K vertices are reported. Analogously to personalized PageRank, the scalable computation of SimRank was first achieved by sampling [12]. Our new SimRank approximation algorithms presented in Section 3 improve the precision of computation.

The key idea of our algorithms is that we use lossy representation of large vectors either by rounding or sketching. Sketches are compact randomized data structures that enable approximate computation in low dimension. To be more precise, we adapt the Count-Min Sketch of Cormode and Muthukrishnan [7], which was primarily introduced for data stream computation. We use sketches for small space computation; in the same spirit Palmer et al. [25] apply probabilistic counting sketches to approximate the sizes of neighborhoods of vertices in large graphs. Further sketching techniques for data streams are surveyed in [23]. Lastly we mention that Count-Min Sketch and the historically first sketch, the Bloom filter [2] stem from the same idea; we refer to the detailed survey [4] for further variations and applications.

Surprisingly, it turns out that sketches do not help if the top $ t$ highest ranked or most similar nodes are queried; the deterministic version of our algorithms show the same performance as the randomized without even allowing a small probability of returning a value beyond the error bound. Here the novelty is the optimal performance of the deterministic method; the top $ t$ problem is known to cause difficulties in sketch-based methods and always increases sketch sizes by a factor of $ \Omega (\log n)$. By using $ \Omega (\log n)$ times larger space we may use a binary search structure or we may use $ p$ sketches accessed $ n^{1/p}$ times per query [7]. Note that $ n^{1/p}$ queries require an error probability of $ O(\delta/n^p)$ that again increase sketch sizes by a factor of $ \Omega (\log n)$.

In Section 4 we show that our algorithms build optimal sized databases. To obtain lower bounds on the database size, we apply communication complexity techniques that are commonly used for space lower bounds [21]. Our reductions are somewhat analogous to those applied by Henzinger et al. [14] for space lower bounds on stream graph computation.

1.2 Preliminaries

We briefly introduce notation, and recall definitions and basic facts about PageRank, SimRank and the Count-Min sketch.


Personalized PageRank

Let us consider the web as a graph. Let $ n$ denote the number of vertices and $ m$ the number edges. Let $ d^+ (v)$ and $ d^- (v)$ denote the number of edges leaving and entering $ v$, respectively. Details of handling nodes with $ d^+ (v) = 0$ and $ d^- (v) = 0$ are omitted.

In [24] the PageRank vector $ p = (p(1)$, ..., $ p(n))$ is defined as the solution of the following equation $ p (u) = c \cdot r (u) + (1 - c) \cdot \sum_{v : (vu) \in E} p (v)/d^+ (v)$, where $ r = (r (1)$, ..., $ r (n))$ is the teleportation vector and $ c$ is the teleportation probability with a typical value of $ c \approx 0.15$. If $ r$ is uniform, i.e. $ r (u) = 1/n$ for all $ u$, then $ {p}$ is the PageRank. For non-uniform $ {r}$ the solution $ {p}$ is called personalized PageRank; we denote it by PPR$ _r$. Since PPR$ _r$ is linear in $ r$ [13,17], it can be computed by linear combination of personalization to single points $ v$, i.e. to vectors $ r = \chi_v$ consisting of all 0 except for node $ v$ where $ \chi_v (v) = 1$. Let PPR$ _v=$PPR$ _{\chi_v}$.

An alternative characterization of PPR$ _u(v)$ [10,17] is based on the probability that a length $ k$ random walk starting at node $ u$ ends in node $ v$. We obtain PPR$ _u(v)$ by choosing $ k$ random according to the geometric distribution:

PPR$\displaystyle ^{[k]}_u (v) = \sum_{v_0=u, v_1, \ldots, v_k = v} \hspace{-.4cm} {1 / (d^+ (v_0) \cdots d^+ (v_{k-1}))};$ (1)
the summation is along walks starting at $ u$ and ending in $ v$. Thus
PPR$\displaystyle _u (v) = \sum_{k' = 0}^\infty c(1-c)^{k'}$ PPR$\displaystyle ^{[k']}_u (v).$ (2)

Similarly we get PPR$ ^{(k)}_u$ if we sum up only to $ k$ instead of $ \infty$. An equivalent reformulation of the path summing formula (2) is the Decomposition Theorem proved by Jeh and Widom [17]:
PPR$\displaystyle _u = c \chi_u + (1-c) \cdot \sum_{v : (uv) \in E}$ PPR$\displaystyle _v / d^+ (u).$ (3)
The Decomposition Theorem immediately gives rise to the Dynamic Programming approach [17] to compute personalized PageRank that performs iterations for $ k=1$, 2, ...with PPR$ ^{(0)}_u = c \cdot \chi_u$:
PPR$\displaystyle ^{(k)}_u = c \chi_u + (1-c) \cdot \sum_{v : (uv) \in E}$ PPR$\displaystyle ^{(k-1)}_v / d^+ (u).$ (4)


SimRank

Jeh and Widom [16] define SimRank by the following equation very similar to the PageRank power iteration such that Sim$ ^{(0)} (u_1,u_2) = \chi_{u_1} (u_2)$ and

Sim$\displaystyle ^{(k)} (u_1,u_2) = \begin{cases}(1-c) \cdot {\sum \mbox{Sim}^{(k-... ... \cdot d^- (u_2)} & \mbox{if }u_1\not=u_2\\ 1& \mbox{if $u_1=u_2$.} \end{cases}$ (5)
where summation is for $ v_1,v_2 : (v_1 u_1),(v_2 u_2) \in E$.


Count-Min Sketch

The Count-Min Sketch [7] is a compact randomized approximate representation of non-negative vector $ x = (x_1$, ..., $ x_n)$ such that a single value $ x_j$ can be queried with a fixed additive error $ \epsilon>0$ and a probability $ \delta>0$ of returning a value out of this bound. The representation is a table of depth $ d = \ln {1/\delta}$ and width $ w = e/\epsilon$. One row $ C$ of the table is computed with a random hash function $ h: \{1,\ldots,n\} \to \{1, \ldots, w\}$. The $ i$th entry of the row $ C$ is defined as $ C_i = \sum_{j : h (j) = i} x_j$. Then the Count-Min sketch table of $ x$ consists of $ d$ such rows with hash functions chosen uniformly at random from a pairwise-independent family.

Theorem 1 (Cormode, Muthukrishnan [7]) Let $ \hat x_j =\min_{C} \{C_{h (j)}\}$ where the minimum is taken over the $ d$ rows of the table. Then $ \hat x_j \ge x_j$ and Prob$ (\hat x_j > x_j + \epsilon\vert\vert x\vert\vert _1) \le \delta$ hold.

Count-Min sketches are based on the principle that any randomized approximate computation with one sided error and bias $ \epsilon'$ can be turned into an algorithm that has guaranteed error at most $ e \cdot\epsilon'$ with probability $ 1-\delta$ by running $ \ln 1/\delta$ parallel copies and taking the minimum. The proof simply follows from Markov's inequality and is described for the special cases of sketch value and inner product in the proofs of Theorems 1 and 2 of [7], respectively.


2 Personalized PageRank

We give two efficient realizations of the dynamic programming algorithm of Jeh and Widom [17]. Our algorithms are based on the idea that if we use an approximation for the partial values in certain iteration, the error will not aggregate when summing over out-edges, instead the error of previous iterations will decay with the power of $ 1-c$. Our first algorithm in Section 2.1 uses certain deterministic rounding optimized for smallest runtime for a given error, while our second algorithm in Section 2.2 is based on Count-Min sketches [7].

The original implementation of dynamic programming [17] relies on the observation that in the first $ k$ iterations of dynamic programming only vertices within distance $ k$ have non-zero value. However, the rapid expansion of the $ k$-neighborhoods increases disk requirement close to $ n^2$ after a few iterations, which limits the usability of this approach2. Furthermore, an external memory implementation would require significant additional disk space.

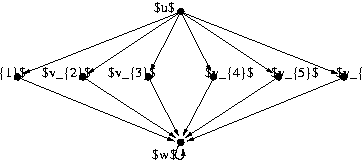
A simple example showing the superiority of dynamic programming over power iterations for small space computations

Figure 1: A simple example showing the superiority of dynamic programming over power iterations for small space computations.

We may justify why dynamic programming is the right choice for small-space computation by comparing dynamic programming to power iteration over the graph of Fig. 1. When computing PPR$ _u (w)$, power iteration moves top-down, starting at $ u$, stepping into its neighbors $ v_1, v_2, \ldots$ and finally adding up all their values at $ w$. Hence when approximating, we accumulate all error when entering the large in-degree node $ w$ and in particular we must compute PPR$ _u (v_i)$ values fairly exact. Dynamic programming, in contrast, moves bottom up by computing the trivial PPR$ _w$ vector, then all the PPR$ _{v_i}$, then finally averages all of them into PPR$ _u$. Because of averaging we do not amplify error at large in-degrees; even better by looking at (4) we notice that the effect of earlier steps diminishes exponentially in $ (1-c)$. In particular even if there are edges entering $ u$ from further nodes, we may safely discard all the small PPR$ _u (v_i)$ values for further computations, thus saving space over power iteration where we require the majority of these values in order to compute PPR$ _u (w)$ with little error.

We measure the performance of our algorithms in the sense of intermediate disk space usage. Notice that our algorithms are two-phase in that they preprocess the graph to a compact database from which value and top list queries can be served real-time; preprocessing space and time is hence crucial for a search engine application. Surprisingly, in this sense rounding in itself yields an optimal algorithm for top list queries as shown by giving a matching lower bound in Section 4. The sketching algorithm further improves space usage by a factor of $ \log n$ and is hence optimal for single value queries. For finding top lists, however, we need additional techniques such as binary searching as in [7] that loose the $ \log n$ factor gain and use asymptotically the same amount of space as the deterministic algorithm. Since the deterministic rounding involves no probability of giving an incorrect answer, that algorithm is superior for top list queries.

The key to the efficiency of our algorithms is the use of small size approximate $ \widehat{\mbox{PPR}}_u^{(k)} (v)$ values obtained either by rounding and handling sparse vectors or by computing over sketches. In order to perform the update step of Algorithm 1 we must access all $ \widehat{\mbox{PPR}}_v$ vectors; the algorithm proceeds as if we were multiplying the weighted adjacency matrix $ A_{u v} = 1/d^+ (u)$ for $ (u v) \in E$ with the vector $ \{\widehat{\mbox{PPR}}_u (w) : u \in V\}$ parallel for all values of $ w$. We may use (semi)external memory algorithms [27]; efficiency will depend on the size of the description of the vectors.

The original algorithm of Jeh and Widom defined by equation (4) uses two vectors in the implementation. We remark that a single vector suffices since by using updated values within an iteration we only speed convergence up. A similar argument is given by McSherry [22] for the power iteration, however there the resulting sequential update procedure still requires two vectors.


2.1 Rounding


\begin{algorithm} % latex2html id marker 1010 [t] \small \caption{PageRank by ... ...\mbox{PPR}}_v/d^+ (u)\Big) $ \ENDFOR \ENDFOR \end{algorithmic}\end{algorithm}

In Algorithm 1 we compute the steps of the dynamic programming personalized PageRank algorithm (4) by rounding all values down to a multiple of the prescribed error value $ \epsilon $. As the sum of PPR$ _u(v)$ for all $ v$ equals one, the rounded non-zeroes can be stored in small space since there may be at most $ 1/\epsilon$ of them.

We improve on the trivial observation that there are at most $ 1/\epsilon$ rounded non-zero values in two ways as described in the next two theorems. First, we observe that the effect of early iterations decays as the power of $ (1-c)$ in the iterations, allowing us to similarly increase the approximation error $ \epsilon_k$ for early iterations $ k$. We prove correctness in Theorem 2; later in Theorem 4 it turns out that this choice also weakens the dependency of the running time on the number of iterations. Second, we show that the size of the non-zeroes can be efficiently bit-encoded in small space; while this observation is less relevant for a practical implementation, this is key in giving an algorithm that matches the lower bound of Section 4.

Theorem 2 Algorithm 1 returns values between PPR$ _u (v) - 2\epsilon/c$ and PPR$ _u(v)$.
Proof. By induction on iteration $ k$ of Algorithm 1 we show a bound that is tighter for $ k=k_{\max}$ than that of the Theorem:
$\displaystyle \vert$PPR$\displaystyle _u (w) - \widehat{\mbox{PPR}}_u (w)\vert < {{1 \over {1-\sqrt{1-c}}} \epsilon_k}. $
By the choice of $ \epsilon $ and $ k_{\max}$ we have $ \epsilon_0 = 1$, thus the $ k=0$ case is immediate since $ 0 \le$ PPR$ _u (v) \le 1$.

Since we use a single vector in the implementation, we may update a value by values that have themselves already been updated in iteration $ k$. Nevertheless since $ \epsilon_k=\sqrt{1-c} \cdot \epsilon_{k-1}$ and hence decreases in $ k$, values that have earlier been updated in the current iteration in fact incur an error smaller than required on the right hand side of the update step of Algorithm 1. In order to distinguish values before and after a single step of the update, let us use $ \widehat{\mbox{PPR}}'$ to denote values on the right hand side. To prove, notice that by the Decomposition Theorem (3)

PPR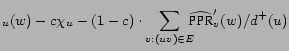$\displaystyle _u(w) - c \chi_u - (1-c) \cdot \sum_{v : (uv) \in E} \hspace{-.2cm} \widehat{\mbox{PPR}}'_v(w)/d^+ (u)$
$\displaystyle = (1-c) \cdot \sum_{v : (u v) \in E} \hspace{-.2cm} {(\mbox{PPR}_v (w) - \widehat{\mbox{PPR}}'_v (w)) / d^+ (u)}$
As $ \psi_k$ introduces at most $ \epsilon_k$ error, by the triangle inequality
$\displaystyle \vert$PPR$\displaystyle _u (w) - \widehat{\mbox{PPR}}_u (w)\vert \hspace{15cm}$

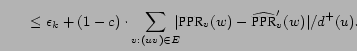$\displaystyle \qquad \le \epsilon_k + (1-c) \cdot \sum_{v : (u v) \in E} \hspac... ...rt\mbox{PPR}_v (w) - \widehat{\mbox{PPR}}'_v (w)\vert / d^+ (u)}. \hspace{10cm}$
Using the inductive hypothesis this leads us to
$\displaystyle \vert$PPR$\displaystyle _u (w) - \widehat{\mbox{PPR}}_u (w)\vert < \epsilon_k + \frac {1-c} {1-\sqrt{1-c}} \cdot \epsilon_{k-1} \hspace{10cm}$
$\displaystyle \qquad = \epsilon_k + \frac {1-c} {1-\sqrt{1-c}} \cdot \frac {\epsilon_{k}} {\sqrt{1-c}} = {1 \over {1-\sqrt{1-c}}} \cdot \epsilon_k, \hspace{10cm}$
completing the proof. $ \qedsymbol$

Next we show that multiples of $ \epsilon $ that sum up to 1 can be stored in $ 1/\epsilon$ bit space. For the exact result we need to select careful but simple encoding methods given in the trivial lemma below.

Lemma 3 Let $ z$ non-negative values be given, each a multiple of $ \epsilon $ that sum up to at most 1. If we unary encode the values as multiples of $ \epsilon $ and use a termination symbol, the encoding uses space $ {1\over\epsilon} + z$ bits. If we combine the same encoding with sparse vector storage by recording the position of non-zeroes in $ \log z$ space each, we may encode the sequence by $ {1\over\epsilon} \cdot (1+\log z)$ bits. $ \Box$
Theorem 4 Algorithm 1 runs in time of $ O (m \log n/ (c \cdot \epsilon))$ bit operations3and builds a database of size $ n \cdot {2\over\epsilon} \cdot \log n$ bits. In order to return the approximate value of PPR$ _u(v)$ and the largest $ t$ elements of PPR$ _u (.)$, we may binary search and sequentially access $ {2\over\epsilon} \cdot \log n$ bits, respectively.
Proof. We determine the running time by noticing that in each iteration $ k$ for each edge we perform addition with the sparse vector PPR$ ^{(k)}$. We may use a linked list of non-zeroes for performing the addition, thus requiring $ O (\log n)$ bit operations for each non-zero of the vector. Since in iteration $ k$ we store all values of a vector with norm at most one rounded down to a multiple of $ \epsilon_k$, we require $ 2/\epsilon_k$ space to store at most $ 1/\epsilon_k$ non-zeroes of PPR$ ^{(k)}$ by Lemma 3. By $ \sum_{k \le k_{\max}} {\sqrt{1-c}^{k_{\max}-k}} < {1 \over {1-\sqrt{1-c}}} < {2 / c}$ the total running time becomes $ O(m\log n /(\epsilon \cdot c))$. $ \qedsymbol$


2.2 Sketching

Next we give a sketch version of Algorithm 1 that improves the space requirement of the rounding based version by a factor of $ \log n$, thus matches the lower bound of Section 4 for value queries. First we give a basic algorithm that uses uniform error bound $ \epsilon $ in all iterations and is not optimized for storage size in bits. Then we show how to gradually decrease approximation error to speed up earlier iterations with less effect on final error; finally we obtain the space optimal algorithm by the bit encoding of Lemma 3.

The key idea is that we replace each PPR$ _u^{(k)}$ vector with its constant size Count-Min sketch in the dynamic programming iteration (4). Let $ S$ denote the sketching operator that replaces a vector by the $ d \times w$ table as in Section 1.2 and let us perform the iterations of (4) with SPPR$ ^{(k)}_u$ and $ S(c \cdot \chi_u)$. Since the sketching operator is trivially linear, in iteration $ k$ we obtain the sketch of the next temporary vector SPPR$ ^{(k)}_u$ from the sketches SPPR$ ^{(k-1)}_v$.

To illustrate the main ingredients, we give the simplest form of a sketch-based algorithm with error, space and time analysis. Let us perform the iterations of (4) with $ e/\epsilon$ wide and $ \ln {1 \over \delta}$ deep sketches $ k^*_{\max}=\log_{1-c}\epsilon$ times; then by Theorem 1 and the linearity of sketching we can estimate PPR$ _u(v)$ for all $ u,v$ from SPPR$ ^{(k^*_{\max})}_u(v)$ with additive error $ 2\epsilon$ and error probability $ \delta $. The personalized PageRank database consists of sketch tables SPPR$ ^{(k^*_{\max})}_u$ for all $ u$. The data occupies $ \Theta({n\over\epsilon}\log{1\over\delta})$ machine words, since we have to store $ n$ tables of reals. An update for node $ u$ takes $ O({{d^+(u)}\over\epsilon}\ln{1\over\delta})$ time by averaging $ d^+(u)$ tables of $ {e\over\epsilon}\times\ln{1\over\delta}$ size and adding $ S(c\chi_u)$, each in $ O(\ln{1\over\delta})$ time. Altogether the required $ k^*_{\max}$ iterations run in $ O({m\over\epsilon}\ln{1\over\delta}\log_{1-c}\epsilon)$ time.

Next we weaken the dependence of the running time on the number of iterations by gradually decreasing error $ \epsilon_k$ as in Section 2.1. When decreasing the error in sketches, we face the problem of increasing hash table sizes as the iterations proceed. Since there is no way to efficiently rehash data into larger tables, we approximate personalized PageRank slightly differently by representing the end distribution of length $ k$ walks, PPR$ ^{[k]}_u$, with their rounded sketches $ \widehat{\mbox{SPPR}}^{[k]}_u$ in the path-summing formula (2):

$\displaystyle \widehat{\mbox{PPR}}_u(v)=\min_{i=1\ldots\ln{1\over\delta}} \Big(\sum_{k=0}^{k_{\max}}c(1-c)^{k}\widehat{\mbox{SPPR}}^{[k]}_u(i,h^i_k(v))\Big)$ (6)
where $ h^i_k$ denotes the $ i$-th hash function of the $ k$-th iteration. By (6) we need to calculate $ \widehat{\mbox{SPPR}}^{[k]}_u$ efficiently in small space. Notice that unlike in the dynamic programming where we gradually increase the precision of $ \widehat{\mbox{PPR}}_u^{(k)}$ as $ k$ grows, we may compute $ \widehat{\mbox{SPPR}}^{[k]}_u$ less precise with growing $ k$ since its values are scaled down by $ (1-c)^k$. Hence we obtain our algorithm by using $ e/\bar{\epsilon}_k=e/\epsilon_{k_{\max} - k}$ wide hash tables in the $ k$-th iteration and replacing the last line of Algorithm 1 with
$\displaystyle \widehat{\mbox{SPPR}}^{[k]}_u \leftarrow \psi_{k_{\max} - k} \Big... ... (uv) \in E}\hspace{-.3cm} \widehat{\mbox{SPPR}}^{[k-1]}_v /d^+ (u) \Big) \Big)$ (7)
where $ \phi_k$ is the recoding function shrinking hash tables from width $ e/\epsilon_{k + 1}$ to $ e/\epsilon_k$. To be more precise, we round the width of each sketch up to the nearest power of two; thus we maintain the error bound, increase space usage by less than a factor of two, and use the recoding function that halves the table when necessary.
Theorem 5 Let us run the sketch version of the dynamic programming Algorithm 1 with sketching to width $ e/\bar{\epsilon}_k$ and rounding all table entries to multiples of $ \bar{\epsilon}_k$ in iteration $ k$. The algorithm runs in time $ O (m \ln {1\over\delta} /(c \cdot \epsilon))$; builds a database of size $ O(n \ln {1\over\delta} /(c \cdot \epsilon))$ bits; and returns a value $ \widehat{\mbox{PPR}}_u (v) \ge \mbox{PPR}_u (v) - \epsilon(1+2/c)$ such that Prob$ (\widehat{\mbox{PPR}_u} (v) > \mbox{PPR}_u (v) + 2\epsilon/c) \le \delta$.
Proof. As $ \sum_{k=0}^{k_{\max}} 1/\bar{\epsilon}_k<2/(\epsilon c)$ still holds, along the same lines as Theorem 4 we immediately get the running time; space follows by Lemma 3.

We err for three reasons: we do not run the iteration infinitely; in iteration $ k$ we round values down by at most $ \bar{\epsilon}_k$, causing a deterministic negative error; and finally the Count-Min Sketch uses hashing, causing a random positive error. For bounding these errors, imagine running iteration (7) without the rounding function $ \psi_k$ but still with $ e/\bar{\epsilon}_k$ wide and $ \ln{1/\delta}$ deep sketches and denote its results by SPPR$ _u^{[k]}$ and define

$\displaystyle \widetilde{\mbox{PPR}}_u(v)=\min_{i=1\ldots\ln{1\over\delta}} \Big(\sum_{k=0}^{k_{\max}}c(1-c)^{k}\mbox{SPPR}^{[k]}_u(i,h^i_k(v))\Big).$
First we upper bound $ \widetilde{\mbox{PPR}}$ to obtain the last claim of the Theorem. Since $ \widehat{\mbox{PPR}}_u(v) \le \widetilde{\mbox{PPR}}_u(v)$, we need Prob$ (\widetilde{\mbox{PPR}}_u(v) > \mbox{PPR}_u(v)+2\epsilon/c) \le \delta$. By the Count-Min principle it is sufficient to show that for a fixed row $ i^*$, the expected overestimation of $ \sum_{k=0}^{k_{\max}}c(1-c)^{k}$SPPR$ ^{[k]}_u(i^*,h^{i^*}_k(v))$ is not greater than $ 2\epsilon/c$. Since the bias of each sketch row SPPR$ ^{[k]}_u(i^*,.)$ is $ \bar{\epsilon}_k$, the bias of their $ c(1-c)^{k}$ exponentially weighted sum is bounded by $ 2\epsilon/c$.

Finally we lower bound $ \widehat{\mbox{PPR}}$; the bound is deterministic. The $ \bar{\epsilon}_k$ loss due to rounding down in iteration $ k$ affects all subsequent iterations, and hence

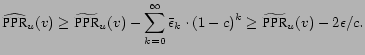$\displaystyle \widehat{\mbox{PPR}}_u(v) \ge \widetilde{\mbox{PPR}}_u(v) - \sum_... ...{\bar{\epsilon}_k \cdot (1-c)^k} \ge \widetilde{\mbox{PPR}}_u(v) - 2\epsilon/c.$
And since we sum up to $ k_{\max}$ instead of infinity, $ \widetilde{\mbox{PPR}}_u(v)$ underestimates PPR$ _u(v)$ by at most $ \epsilon^2 \le \epsilon$, proving the Theorem. $ \qedsymbol$


3 SimRank

In this section first we give a simpler algorithm for serving SimRank value and top-list queries that combines rounding with the empirical fact that there are relatively few large values in the similarity matrix. Then in Section 3.1 we give an algorithm for SimRank values that uses optimal storage in the sense of the lower bounds of Section 4. Of independent interest is the main component of the algorithm that reduces SimRank to the computation of values similar to personalized PageRank.

SimRank and personalized PageRank are similar in that they both fill an $ n\times n$ matrix when the exact values are computed. Another similarity is that practical queries may ask for the maximal elements within a row. Unlike personalized PageRank however, when rows can be easily sketched and iteratively computed over approximate values, the $ n\times n$ matrix structure is lost within the iterations for Sim$ (v_1,v_2)$ as we may have to access values of arbitrary Sim$ (u_1,u_2)$. Even worse $ \sum_{u,v}$PPR$ _u (v) = n$ while

$\displaystyle M = \sum_{u_1,u_2}$Sim$\displaystyle (u_1,u_2)$
can in theory be as large as $ \Omega (n^2)$; an $ O (n)$-size sketch may hence store relevant information about personalized PageRank but could not even contain values below 1 for SimRank. An example of a sparse graph with $ M=\Omega (n^2)$ is an $ n$-node star where Sim$ (u,v)=1-c$ for all pairs other than the center.

In practice $ M$ is expected be a reasonable constant times $ n$. Hence first we present a simple direct algorithm that finds the largest values within the entire Sim$ (u_1,u_2)$ table. In order to give a rounded implementation of the iterative SimRank equation (5), we need to give an efficient algorithm to compute a single iteration. The naive implementation requires $ \Omega(1)$ time for each edge pair with a common source vertex that may add up to $ \Omega (n^2)$. Instead for $ u_1 \not= u_2$ we will compute the next iteration with the help of an intermediate step when edges out of only one of the two vertices are considered:

ASim$\displaystyle ^{(k)} (u_1,v_2)$ $\displaystyle =$ $\displaystyle {\sqrt{1-c} \over d^- (u_1)} \sum_{v_1: (v_1 u_1) \in E}$ Sim$\displaystyle ^{(k-1)} (v_1,v_2)$ (8)
Sim$\displaystyle ^{(k)} (u_1,u_2)$ $\displaystyle =$ $\displaystyle {\sqrt{1-c} \over d^- (u_2)} \sum_{v_2: (v_2 u_2) \in E}$ ASim$\displaystyle ^{(k)} (u_1,v_2)$ (9)

Along the same line as the proof of Theorems 2 we prove that (i) by rounding values in iterations (8-9) we approximate values with small additive error; (ii) the output of the algorithm occupies small space; and (iii) approximate top lists can be efficiently answered from the output. The proof is omitted due to space limitations. We remark here that (8-9) can be implemented by 4 external memory sorts per iteration, in two of which the internal space usage can in theory grow arbitrary large even compared to $ M$. This is due to the fact that we may round only once after each iteration; hence if for some large out-degree node $ v$ a value Sim$ ^{(k-1)} (v,v_2)$ is above the rounding threshold or ASim$ ^{(k)} (u_1,v)$ becomes positive, then we have to temporarily store positive values for all out-neighbors, most of which will be discarded when rounding.

Theorem 6 Let us iterate (8-9) $ k_{\max} = 4\log_{1-c}\epsilon$ times by rounding values in iteration $ k$ down to multiples of $ \epsilon_k= \epsilon \cdot (1-c)^{-{k_{\max}-k \over 4}}$ for (9) and $ \epsilon_{k-1}+\epsilon_k$ for (8).


(i)
The algorithm returns approximate values for $ u \ne v$ with
Sim$ (u,v) \ge \widehat{\mbox{Sim}}(u,v) \ge \mbox{Sim}(u,v) - 4\epsilon/c$.


(ii)
The space used by the $ \widehat{\mbox{Sim}}(u,v)$ values is $ O(M \cdot{2\over\epsilon} \cdot \log n)$ bits where $ M=\sum_{u,v}$Sim$ (u,v)$.


(iii)
Top list queries can be answered after positive $ \widehat{\mbox{Sim}}(u,\cdot)$ values are sorted for each $ u$ in $ O(M \cdot{2\over\epsilon} \cdot \log^2 n)$ time.



3.1 Reduction of SimRank to PPR

Now we describe a SimRank algorithm that uses a database of size matching the corresponding lower bound of Section 4 by taking advantage of the fact that large values of similarity appear in blocks of the $ n\times n$ similarity table. The blocking nature can be captured by observing the similarity of Sim$ _{v_1,v_2}$ to the product PPR$ _{v_1}\cdot$PPR$ _{v_2}$ of vectors PPR$ _{v_1}$ and PPR$ _{v_2}$.

We use the independent result of [10,17,16] that PageRank type values can be expressed by summing over endpoints of walks as in equation (1). First we express SimRank by walk pair sums, then we show how SimRank can be reduced to personalized PageRank by considering pairs of walks as products. Finally we give sketching and rounding algorithms for value and top queries based on this reduction.

In order to capture pairs of walks of equal length we define ``reversed'' PPR by using walks of length exactly $ k$ by modifying (1):

RP$\displaystyle ^{[k]}_v (u) = \sum_{v_0=v, v_1, \ldots, v_k = u} {1 / (d^- (v_1) \cdots d^- (v_{k}))}$ (10)
where $ v_0$, ..., $ v_k$ is a walk from $ v$ to $ u$ on the transposed graph. Similarly [16] shows that Sim$ ^{(k)}_{v_1,v_2}$ equals the total weight of pairs
$\displaystyle v_1 = w_0, w_1, \ldots, w_{k'-1}, w_{k'}$ $\displaystyle =$ $\displaystyle u$
$\displaystyle v_2 = w'_0, w'_1, \ldots, w'_{k'-1}, w'_{k'}$ $\displaystyle =$ $\displaystyle u$
with length $ k' \le k$ that both end at $ u$ and one of them comes from $ v_1$ while the other one from $ v_2$. The weight of the pair of walks is the expected $ (1-c)$ meeting distance as defined in [16]:
$\displaystyle (1-c)^{k'} / (d^- (w_1) \cdots d^- (w_{k'}) \cdot d^- (w'_1) \cdots d^- (w'_{k'}))$ (11)
Importantly the walks satisfy two properties: they have (i) equal length and (ii) no common vertex at the same distance from start, i.e. $ w_i \not= w'_i$ for $ i \ne k'$. Except for the last two requirements Sim$ ^{(k)}_{v_1,v_2}$ has a form similar to the inner product of PPR$ _{v_1}$ and PPR$ _{v_2}$ on the reversed graph by (1).

Next we formalize the relation and give an efficient algorithm that reduces SimRank to PPR on the reversed graph. As a ``step 0 try'' we consider

Sim$\displaystyle ^{(0)}_{v_1,v_2} = \sum_{k>0} (1-c)^k \sum_u$RP$\displaystyle ^{[k]}_{v_1} (u)$RP$\displaystyle ^{[k]}_{v_2} (u)$ (12)
with form similar to SimRank with exact length $ k$ walks except that these walks may have common vertices unlike stated in (ii).


\begin{algorithm} % latex2html id marker 1608 [t] \small \caption{SimRank by r... ...}}(v)$\ to multiples of $\epsilon$. } \ENDFOR \end{algorithmic}\end{algorithm}

In order to exclude pairs of walks that meet before ending, we use the principle of inclusion and exclusion. We count pairs of walks that have at least $ t$ meeting points after start as follows. Since after their first meeting point $ v$ the walks proceed as if computing the similarity of $ v$ to itself, we introduce a self-similarity measure by counting weighted pairs of walks that start at $ v$ and terminate at the same vertex $ u$ by extending (12):

SSim$\displaystyle ^{(0)} (v) = \sum_u \sum_{k>0} (1-c)^{k}$ RP$\displaystyle ^{[k]}_v(u)$ RP$\displaystyle ^{[k]}_v(u)$ (13)
Now we may recursively define a value that counts all pairs of walks with at least $ t+1$ inner points where the walks meet; the values below in fact count each pair $ s \choose {t+1}$ times that meet at exactly $ s$ inner points. First we define self-similarity as
SSim$\displaystyle ^{(t+1)} (v) = \sum_u \sum_{k>0} (1-c)^{k}$RP$\displaystyle ^{[k]}_v(u)$ RP$\displaystyle ^{[k]}_v (u) \cdot$ SSim$\displaystyle ^{(t)} (u)$ (14)
and then similarity with at least $ t+1$ inner meeting points as
Sim$\displaystyle ^{(t+1)}_{v_1,v_2} = \sum_u \sum_{k>0} (1-c)^{k}$RP$\displaystyle ^{[k]}_{v_1} (u)$ RP$\displaystyle ^{[k]}_{v_2} (u) \cdot$ SSim$\displaystyle ^{(t)} (u).$ (15)
By the principle of inclusion and exclusion
Sim$\displaystyle (v_1,v_2) =$ Sim$\displaystyle ^{(0)}_{v_1,v_2} -$ Sim$\displaystyle ^{(1)}_{v_1,v_2} +$ Sim$\displaystyle ^{(2)}_{v_1,v_2} - \ldots$ (16)
where Sim$ ^{(0)}$ is defined in (12) as the weighted number of walk pairs that are unrestricted in the number of meeting times. Induction on $ t$ shows that Sim$ ^{(t)}_{v_1,v_2} \le \left({1-c \over c}\right)^{t+1}$, thus the infinite series (16) is (absolute) convergent if $ {1-c \over c}<1$. By changing the order of summation (16) becomes
Sim$\displaystyle (v_1,v_2)$ $\displaystyle =$ $\displaystyle \sum_{k>0} (1-c)^{k} \sum_u$RP$\displaystyle ^{[k]}_{v_1} (u)$ RP$\displaystyle ^{[k]}_{v_2} (u) \cdot$ SSim$\displaystyle (u),$ where
SSim$\displaystyle (u)$ $\displaystyle =$ $\displaystyle 1- \sum_{t\ge0} (-1)^t$ SSim$\displaystyle ^{(t)} (u).$ (17)

The proof of the main theorems below are omitted due to space limitations.

Theorem 7 If $ c>1/2$ Algorithm 2 uses $ n \cdot {4\over c\epsilon} \cdot \log n$ bits to store $ \widehat{\mbox{RP}}^{[k]}$ and $ \widehat{\mbox{SSim}}^{(t)}$ values; the $ \log n$ factor can be replaced by $ e\log 1/\delta$ by sketching $ \widehat{\mbox{RP}}^{[k]}$ in width $ e/\epsilon_{k_{\max} - k}$. The algorithm computes these values in $ O((m+n\log_{1-c \over c}\epsilon) / (c\epsilon))$ time measured in RAM operations and approximates $ \widehat{\mbox{Sim}}(v_1,v_2)$ in $ O(\log n/ (c\epsilon))$ bit operations time. For given $ v_1$ the set $ S$ of non-negative $ \widehat{\mbox{Sim}}(v_1,v_2)$ values can be computed in bit operations time $ O(\vert S\vert\log n/ (c\epsilon))$.
Theorem 8 If $ c>1/2$ the above algorithm gives $ \vert\widehat{\mbox{Sim}}_{v_1,v_2} - \mbox{Sim}_{v_1,v_2}\vert = O (\epsilon/(c-1/2)^2)$; when sketching RP, this holds with probability at least $ 1-\delta$.


4 Lower bounds

In this section we will prove lower bounds on the database size of approximate PPR algorithms that achieve personalization over a subset of $ H$ vertices. More precisely we will consider two-phase algorithms: in the first phase the algorithm has access to the edge set of the graph and has to compute a database; in the second phase the algorithm gets a query and has to answer by accessing the database, i.e. the algorithm cannot access the graph during query-time. A $ b(H)$ worst case lower bound on the database size holds, if for any two-phase algorithm there exists a personalization input such that a database of size $ b(H)$ bits is built in the first phase.

We will consider the following queries for $ 0 \leq \epsilon,\delta,\phi \leq 1$:

$ \bullet$
$ \epsilon $-$ \delta $ value approximation: given the vertices $ u,v$ approximate $ \ensuremath{\mbox{PPR}}_u(v)$ with $ \ensuremath{\widehat{\mbox{PPR}}}_u(v)$ such that
$\displaystyle \ensuremath{\mathop{\mbox{Prob}}}\{ \vert \ensuremath{\mbox{PPR}}... ...- \ensuremath{\widehat{\mbox{PPR}}}_u(v) \vert \leq \epsilon \} \geq 1-\delta. $
$ \bullet$
$ \phi-\epsilon-\delta$ top query: given the vertex $ u$, with probability $ 1-\delta$ compute the set of vertices $ W$ which have personalized PPR values according to vertex $ u$ greater than $ \phi$. Precisely we require the following:
$\displaystyle \forall w\in V$ $\displaystyle :$ $\displaystyle \ensuremath{\mbox{PPR}}_{u}(w) \geq \phi \Rightarrow w\in W$
$\displaystyle \forall w\in W$ $\displaystyle :$ $\displaystyle \ensuremath{\mbox{PPR}}_{u}(w) \geq \phi - \epsilon$

As Theorem 6 of [11] shows, any two-phase PPR algorithm solving the exact ( $ \epsilon=0$) PPR value problem requires an $ \Omega((1-2\delta)\vert H\vert \cdot n)$ bit database. Our tool towards the lower bounds will be the asymmetric communication complexity game bit-vector probing [14]: there are two players $ A$ and $ B$; player $ A$ has a vector $ x$ of $ m$ bits; player $ B$ has a number $ y \in \{1,2,\dots,m\}$; and they have to compute the function $ f(x,y)=x_y$, i.e., the output is the $ y$th bit of the input vector $ x$. To compute the proper output they have to communicate, and communication is restricted in the direction $ A\rightarrow B$. The one-way communication complexity [21] of this function is the number of transferred bits in the worst case by the best protocol.

Theorem 9 ([14]) Any protocol that outputs the correct answer to the bit-vector probing problem with probability at least $ \frac{1+\gamma}2$ must transmit at least $ \gamma m$ bits.

Now we are ready to state and prove our lower bounds, which match the performance of the algorithms presented in Sections 2 and 3.1, hence showing that they are space optimal.

Theorem 10 Any two-phase $ \epsilon $-$ \delta $ PPR value approximation algorithm with $ \epsilon,\delta>0$ builds a database of $ \Omega( \frac 1 \epsilon \cdot \log \frac 1 \delta \cdot \vert H\vert )$ bits in worst case, when the graph has at least $ \vert H\vert+\frac{1-c}{8\epsilon\delta}$ nodes.
Proof. We prove the theorem by reducing the bit vector probing problem to the $ \epsilon $-$ \delta $ approximation. Given a vector $ x$ of $ m=\Omega( \frac 1 \epsilon \cdot \log \frac 1 \delta \cdot \vert H\vert )$ bits, player $ A$ will construct a graph and compute a PPR database with the first phase of the $ \epsilon $-$ \delta $ approximation algorithm. Then $ A$ transmits this database to $ B$. Player $ B$ will perform a sequence of second-phase queries such that the required bit $ x_y$ will be computed with error probability $ \frac 1 4$. The above outlined protocol solves the bit vector probing with error probability $ \frac 1 4$. Thus the database size that is equal to the number of transmitted bits is $ \Omega(m)=\Omega(\frac 1 \epsilon \cdot \log \frac 1 \delta \cdot \vert H\vert )$ in worst case by Theorem 9. It remains to show the details of the graph construction on $ A$'s side and the query algorithm on $ B$'s side.

Given a vector $ x$ of $ m= \frac {1-c} {2\epsilon} \cdot \log \frac 1 {4\delta} \cdot \vert H\vert $ bits, $ A$ constructs the ``bipartite'' graph with vertex set $ \{ u_i : i=1, \ldots, \vert H\vert\} \cup \{ v_{j,k} : j=1, \ldots, \frac{1-c}{2\epsilon}, k=1, \ldots, \frac 1 {4\delta} \}.$ For the edge set, $ x$ is partitioned into $ \frac {1-c}{2\epsilon} \cdot \vert H\vert$ blocks, where each block $ b_{i,j}$ contains $ \log \frac 1 {4\delta} $ bits for $ i=1, \ldots, \vert H\vert$, $ j= 1, \ldots, \frac{1-c}{2\epsilon}$. Notice that each $ b_{i,j}$ can be regarded as a binary encoded number with $ 0 \le b_{i,j} < \frac{1}{4\delta}$. To encode $ x$ into the graph, $ A$ adds an edge $ (u_i, v_{j,k})$ iff $ b_{i,j}=k$, and also attaches a self-loop to each $ v_{j,k}$. Thus the $ \frac{1-c}{2\epsilon}$ edges outgoing from $ u_i$ represent the blocks $ b_{i,1}, \ldots, b_{i,(1-c)/{2\epsilon}}$.

After constructing the graph $ A$ computes an $ \epsilon $-$ \delta $ approximation PPR database with personalization available on $ u_1,\ldots, u_{\vert H\vert}$, and sends the database to $ B$, who computes the $ y$th bit $ x_y$ as follows. Since $ B$ knows which of the blocks contains $ x_y$ it is enough to compute $ b_{i,j}$ for suitably chosen $ i,j$. The key property of the graph construction is that $ \ensuremath{\mbox{PPR}}_{u_i}(v_{j,k})= \frac {1-c} {d^+(u_i)} = 2 \epsilon$ iff $ b_{i,j}=k$ otherwise $ \ensuremath{\mbox{PPR}}_{u_i}(v_{j,k})= 0$. Thus $ B$ computes $ \ensuremath{\widehat{\mbox{PPR}}}_{u_i}(v_{j,k})$ for $ k=1,\ldots, \frac 1 {4\delta}$ by the second phase of the $ \epsilon $-$ \delta $ approximation algorithm. If all $ \ensuremath{\widehat{\mbox{PPR}}}_{u_i}(v_{j,k})$ are computed with $ \vert \ensuremath{\mbox{PPR}}_{u_i}(v_{j,k}) - \ensuremath{\widehat{\mbox{PPR}}}_{u_i}(v_{j,k})\vert \leq \epsilon$, then $ b_{i,j}$ containing $ x_y$ will be calculated correctly. By the union bound the probability of miscalculating any of $ \ensuremath{\widehat{\mbox{PPR}}}_{u_i}(v_{j,k})$ is at most $ \frac 1 {4 \delta} \cdot \delta = \frac 1 4$. $ \qedsymbol$

Theorem 11 Any two-phase PPR algorithm solving the top query problem with parameters $ \epsilon>0$, $ \delta \ge 0$ builds a database of $ \Omega( \frac{1-2\delta}\epsilon \vert H\vert\log n)$ bits in worst case, when the graph has
$ n \ge 2\vert H\vert+\left(\frac{1-c}{2\epsilon}\right)^2$ nodes.
Proof. We will proceed according to the proof of Theorem 10.

Let $ \phi=2\epsilon$ and $ k=\lfloor \frac{1-c}{2\epsilon}\rfloor$ and the graph have nodes $ \{ u_i : i=1, \ldots, \vert H\vert\} \cup \{ v_j : j=1, \ldots, n^*\}$ (with $ n^*=n-\vert H\vert$). By the assumptions on the vertex count, $ n^*=\Omega(n)$ and $ \sqrt n^* \geq k$.

Let the size of the bit-vector probing problem's input be $ m=\vert H\vert\cdot k\cdot \log n^* / 2$. Assign each of the $ k\cdot \log n^* / 2$ sized blocks to a vertex $ u_i$ and fix a code which encodes these bits into $ k$-sized subsets of the vertices $ \{v_j\}$. This is possible, as the number of subsets is $ \binom{n^*}{k}>(\frac {n^*}k)^k \geq {\sqrt n^*}^k$. These mappings are known to both parties $ A$ and $ B$. Note that due to the constraints on $ n^*,k,\vert H\vert$ and $ n$ we have $ k\cdot \log n^* / 2 = \Omega(\frac 1\epsilon \log n)$.

Given an input bit-vector of $ A$, for each vertex $ u_i$ take its block of bits and compute the corresponding subset of vertices $ \{v_j\}$ according to the fixed code. Let $ u_i$ have an arc into these vertices. Let all vertices $ v_j$ have a self-loop. Now $ A$ runs the first phase of the PPR algorithm and transfers the resulting database to $ B$.

Given a bit index $ y$, player $ B$ determines its block, and issues a top query on the representative vertex, $ u_i$. As each of the out-neighbors $ w$ of $ u_i$ has $ \ensuremath{\mbox{PPR}}_{u_i}(w)=\frac{1-c}{d^+(u_i)}=\frac{1-c}k\geq\phi$, and all other nodes $ w'$ have $ \ensuremath{\mbox{PPR}}_{u_i}(w')=0$, the resulting set will be the set of out-neighbors of $ u_i$, with probability $ 1-\delta$. Applying the inverse of the subset encoding, we get the bits of the original input vector, thus the correct answer to the bit-vector probing problem. Setting $ \frac{1+\gamma}2=1-\delta$ we get that the number of bits transmitted, thus the size of the database was at least $ \Omega(\gamma \vert H\vert \cdot k\cdot \log n^* / 2) =\Omega(\frac{1-2\delta}\epsilon \vert H\vert\log n)$. $ \qedsymbol$

We remark that using the graph construction in the full version of [12] it is straightforward to modify Theorems 10 and 11 to obtain the same space lower bounds for SimRank as well. Moreover, it is easy to see that Theorem 11 holds for the analogous problem of approximately reporting the top $ t=1/\phi$ number vertices with the highest PageRank or SimRank scores respectively.

With the graph construction of Theorem 10 at hand, it is possible to bypass the bit-vector probing problem and reduce the approximate personalized PageRank value query to similar lower bounds for the Bloom filter [4] or to a weaker form for the Count-Min sketch [8]. However, to the best of our knowledge, we are unaware of previous results similar to Theorem 11 for the top query.


5 Experiments

This section presents our personalized PageRank experiments on 80M pages of the 2001 Stanford WebBase crawl [15]. The following questions are addressed by our experiments:

$ \bullet$
How does the rounding error affect the quality and running time of the rounded dynamic programming algorithm? We confirm that the maximum error drops linearly in the rounding error $ \epsilon $, and find that running times increase sublinearly with $ 1/\epsilon$, making rounded dynamic programming particularly scalable.
$ \bullet$
How do the qualities of the various algorithms relate to each other? We conclude that rounded dynamic programming outperforms all the other methods by a large margin.

5.1 Measuring the Quality of Approximate PageRank Scores

We compare our approximate PPR scores to exact PPR scores computed by the personalized PageRank algorithm of Jeh and Widom [17] with a precision of $ 10^{-8}$ in $ L_1$ norm. In the experiments we set teleportation constant $ c$ to its usual value $ 0.15$, and personalize on a single page $ u$ chosen uniformly at random from all vertices. The experiments were carried out with 1000 independently chosen personalization node $ u$, and the results were averaged.

To compare the exact and approximate PPR scores personalized to page $ u$, we measure the difference between top score lists of exact $ \ensuremath{\mbox{PPR}}_u$ and approximate $ \ensuremath{\widehat{\mbox{PPR}}}_u$ vectors. The length $ t$ of the compared top lists is in the range 5 to 1000, which is the usual maximum length of the results returned by search engines.

The comparison of top lists is key in measuring the goodness of a ranking method [9, and the references therein] or the distortion of a PageRank encoding [13]. Let $ \ensuremath{T_t^u}$ denote the set of pages having the $ t$ highest personalized PageRank values in the vector PPR$ _u$ personalized to a single page $ u$. We approximate this set by $ \ensuremath{\widehat{T_t^u}}$, the set of pages having the $ t$ highest approximated scores in vector $ \ensuremath{\widehat{\mbox{PPR}}}_u$. We will apply the following three measures to compare the exact and approximate rankings of $ \ensuremath{T_t^u}$ and $ \ensuremath{\widehat{T_t^u}}$. The first two measures will determine the overall quality of the approximated top-$ t$ set $ \ensuremath{\widehat{T_t^u}}$, as they will be insensitive to the ranking of the elements within $ \ensuremath{\widehat{T_t^u}}$.

Relative aggregated goodness [26] measures how well the approximate top-$ t$ set performs in finding a set of pages with high total personalized PageRank. It calculates the sum of exact PPR values in the approximate set compared to the maximum value achievable (by using the exact top-$ t$ set $ \ensuremath{T_t^u}$):

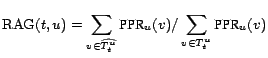
$\displaystyle \ensuremath{\mathop{\mathrm{RAG}}}(t,u)= \sum_{v\in \ensuremath{\... ...h{\mbox{PPR}}_u(v) / \sum_{v\in\ensuremath{T_t^u}}\ensuremath{\mbox{PPR}}_u(v) $

We also measure the precision of returning the top-$ t$ set (note that as the sizes of the sets are fixed, precision coincides with recall). If all exact PPR scores were different we could simply define precision as $ \frac{\vert\ensuremath{\widehat{T_t^u}}\cap\ensuremath{T_t^u}\vert}t$. Treating nodes with equal exact PPR scores in a more liberal way we define precision as

$\displaystyle \ensuremath{\mathop{\mathrm{Prec}}}(t,u)= \vert v\in\ensuremath{\... ...}}_u(v) \ge \min_{w\in\ensuremath{T_t^u}}\ensuremath{\mbox{PPR}}_u(w)\vert / t $

The third measure, Kendall's $ \tau$ compares the exact ranking with the approximate ranking in the top-$ t$ set. Note that the exact PPR list of nodes with a small neighborhood or the tail of approximate PPR ranking may contain a large number of ties (nodes with equal scores) that may have a significant effect on rank comparison. Versions of Kendall's $ \tau$ with different tie breaking rules appear in the literature, we use the original definition as e.g. in [19]. Ignoring ties for the ease of presentation, the rank correlation Kendall's $ \tau$ compares the number of pairs ordered the same way in both rankings to the number of reversed pairs; its range is $ [-1,+1]$, where $ -1$ expresses complete disagreement, $ +1$ represents a perfect agreement. To restrict the computation to the top $ t$ elements, we took the union of the exact and approximated top-$ t$ sets $ \ensuremath{T_t^u}\cup\ensuremath{\widehat{T_t^u}}$. For each ordering, all nodes that were outside the orderings' top-$ t$ set were considered to be tied and ranked strictly smaller than any node contained in its top-$ t$ set.


5.2 Breadth First Search Heuristic

One of our baselines in our experiments is a heuristically modified power iteration algorithm. While the example of Figure 1 shows that we may get large error even by discarding very small intermediate values, a heuristic that delays the expansion of nodes with small current PageRank values [17,22,6] still achieves good results on real world data.

When personalizing to node $ u$, let us start from $ \chi_u$ and keep a dedicated list of the non-zero entries, which we expand breadth first. This allows us to perform one iteration quickly as long as these lists are not too long; we cease the expansion if we have reached the value $ S$. Moreover we skip the expansion originating from a node if its current PageRank divided by the outdegree is below a given threshold $ E$. Finally we never let the number of iteration exceed the predetermined value $ K$. We experimented with a variant of McSherry's state of the art update iteration [22], as well as a scheme to reuse the previous node's result, but neither of them produced better approximation within the same running time, hence we do not report these results.


5.3 Results

We conducted our experiments on a single AMD Opteron 2.0 GHz machine with 4 GB of RAM under Linux OS. We used a semi-external memory implementation for rounded dynamic programming, partitioning the intermediate $ \widehat{\mbox{PPR}}^{(k)}_u(w)$ vectors along the coordinate $ w$. Using a single vector allowed us to halve the memory requirements by storing the intermediate results in a FIFO like large array, moving the $ \widehat{\mbox{PPR}}^{(k)}_u$ being updated from the head of the queue to its tail. We stored the PageRank values as multiples of the rounding error $ \epsilon $ using a simple but fast variable length byte-level encoding. We did not partition the vector $ \widehat{\mbox{PPR}}^{(k)}_u(w)$ into predefined subsets of $ w$; instead as the algorithm ran out of memory, it split the current set of $ w$ and checkpointed one half to disk. Once the calculation in the first half was finished, it resumed in the second half, resulting in a Depth First Search like traversal of subsets of $ w$. Since dynamic programming accesses the edges of the graph sequentially, we could overlay the preloading of the next batch of edges with the calculations in the current batch using either asynchronous I/O or a preloader thread. This way we got the graph I/O almost for free. It is conceivable that reiterations [22] or the compression of vertex identifiers [3] could further speed up the computation. For implementations on a larger scale one may use external memory sorting with the two vector dynamic programming variant. Or, in a distributed environment, we may partition the graph vertices among the cluster nodes, run a semi-external memory implementation on each node and exchange the intermediate results over the network as required. To minimize network load, a partition that respects the locality of links (e.g. hostname based) is advisable.

In our first experiment we demonstrate the convergence of rounded dynamic programming measured by the maximum error as the number of iterations increases whilst keeping $ \epsilon $ fixed at a modest $ 10^{-4}$ in all iterations. On Figure 2, left, it can be clearly seen that the underlying exact dynamic programming converges in far fewer iterations than its worst case bound of $ \log_{1-c}\epsilon=57$ and that the maximum error due to rounding is roughly one half of the bound $ \epsilon/c\approx7\cdot10^{-4}$ provable for the simplified algorithm that rounds to fixed $ \epsilon $ in all iterations. On Figure 2, right we see the goodness of the approximate ranking improving the same way as maximum error drops. This is theoretically clear since at maximum one-sided error of $ \epsilon'$ we never swap pairs in the approximate rankings with exact PageRank values at least $ \epsilon'$ apart. In the chart we set the top set size $ t$ to 200.

Effect of the number of iterations

Figure: Effect of the number of iterations $ k_{\max}$ with $ \epsilon =10^{-4}$ rounding error.

Based on the experiences of Figure 2 we set the number of iterations $ k_{\max}$ to a conservative $ 35$ and investigated the effects of the error $ \epsilon $, using rounding to varying $ \epsilon_k$ as in Algorithm 1. The straight line on Figure 3, left clearly indicates that rounding errors do not accumulate and the maximum error decreases linearly with the rounding error as in Theorem 2. Additionally the error is much smaller than the worst case bound4, for example at $ \epsilon=10^{-5}$ it is $ 3.5\cdot10^{-5}$ vs. $ 20\cdot10^{-5}$. The running time scales sublinearly in $ 1/\epsilon$ (e.g. from 3.5 hours to 14 hours when moving from $ \epsilon=10^{-3}$ to $ \epsilon =10^{-4}$) as it is governed by the actual average number of PPR$ _u$ entries being above $ \epsilon $ and not the worst case upper estimate $ 1/\epsilon$. The same observation applies to the database size, which requires 201 GB for $ \epsilon=10^{-5}$. The right panel of Figure 3 demonstrates that the approximate ranking improves accordingly as we move to smaller and smaller $ \epsilon $ (we set the top set size $ t$ to 100).

Effect of the rounding error

Figure 3: Effect of the rounding error $ \epsilon $ with $ k_{\max}=35$ iterations.

We now turn to the experimental comparison of personalized PageRank approximation algorithms summarized in Table 2. For the BFS heuristic and the Monte Carlo method we used an elementary compression (much simpler and faster than [3]) to store the Stanford WebBase graph in 1.6 GB of main memory, hence the semi-external dynamic programming started with a handicap. Finally we mention that we did not apply rounding to the sketches.


Table 2: Summary of approximate personalized PageRank algorithms and heuristics.

\begin{table} % latex2html id marker 6403 % \begin{tabularx}{\linewidth}{\vert X... ...~\ref{sect:expheur} & 3.5 days \tabularnewline \hline \end{tabularx}\end{table}

It is possible to enhance the precision of most of the above algorithms by applying the neighbor averaging formula (4) over the approximate values once at query time. We applied this trick to all algorithms, except for the sketches (where it does not make a difference), which resulted in slightly higher absolute numbers for larger top lists at a price of a tiny drop for very short top lists, but did not affect the shape or the ordering of the curves. Due to the lack of space, we report neighbor averaged results only.

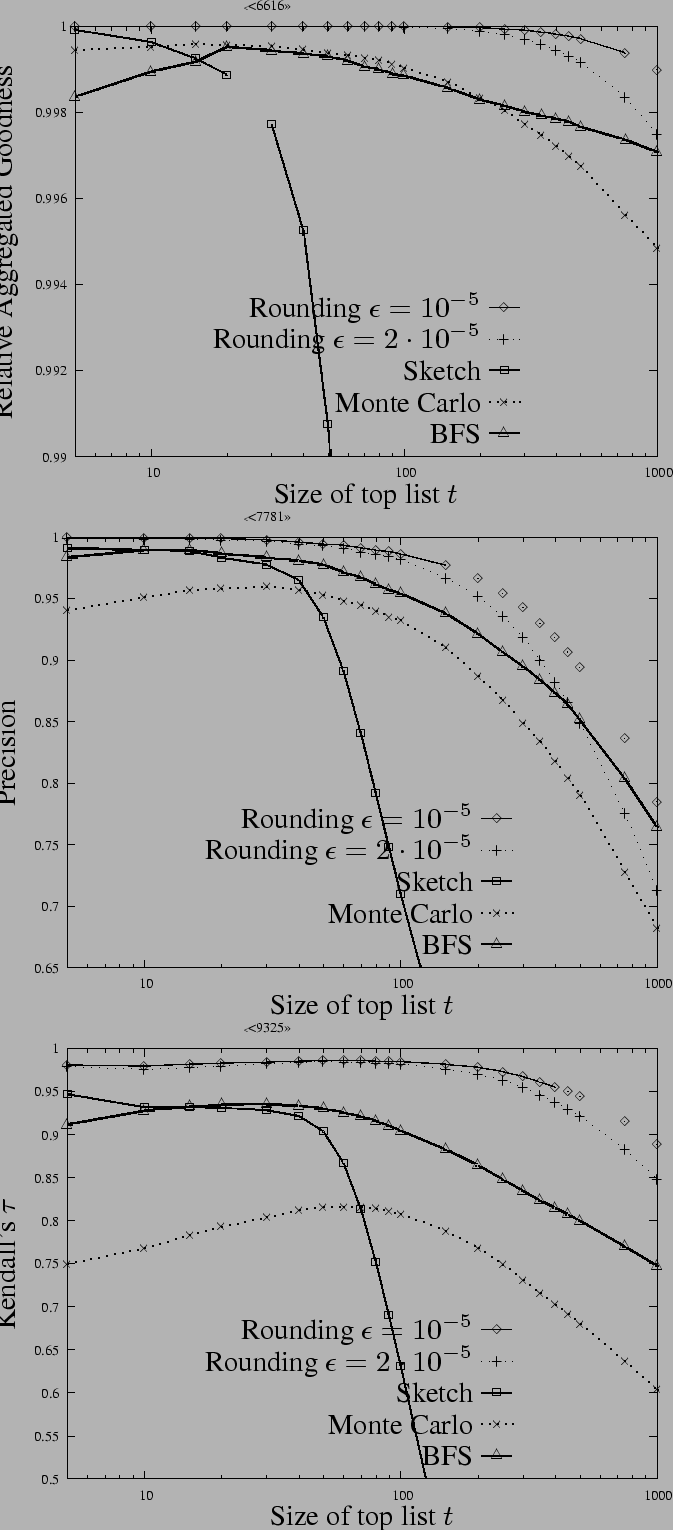
Empirical comparison of approximate personalized PageRank algorithms

Figure: Empirical comparison of approximate personalized PageRank algorithms according to three measures of goodness and varying top set size $ t$ without (left) and with (right) neighbor averaging.

All three measures of Figure 4 indicate that as the top list size increases, the task of approximating the top-$ t$ set becomes more and more difficult. This is mainly due to the fact that among lower ranked pages the personalized PageRank difference is smaller and hence harder to capture using approximation methods. As expected, RAG scores are the highest, and the strictest Kendall's $ \tau$ scores are the smallest with precision values being somewhat higher than Kendall's $ \tau$.

Secondly, the ordering of the algorithms with respect to the quality of their approximate top lists is fairly consistent among Relative Aggregated Goodness, Precision and Kendall's $ \tau$. Rounded dynamic programming performs definitely the best, moreover its running times are the lowest among the candidates. The runner up Breadth-First Search heuristic and Monte Carlo sampling seem to perform similarly with respect to Relative Aggregated Goodness with Monte Carlo sampling underperforming in the precision and Kendall's $ \tau$ measures. Although sketching is quite accurate for single value queries with an average additive error of , its top list curve drops sharply at size $ t$ around . This is due to the fact that and hence a large number of significantly overestimated vertices crowd out the true top list. Based on these findings, for practical applications we recommend rounded dynamic programming with neighbor averaging , which achieves solid precision and rank correlation (at or above ) over the top pages with reasonable resource consumption.

Lastly we remark that preliminary SimRank experiments over the same WebBase graph indicate that Algorithm 2 outperforms iterations (8-9) when using an equal amount of computation. Additionally SimRank scores computed by Algorithm 2 achieve marginally weaker agreement (Kruskal-Goodman ) with the Open Directory Project (http:/http:/dmoz.orghttp:/dmoz.org) as Monte Carlo sampling ( ) [12] but with higher recall.

6 Conclusions and Future work

We presented algorithms for the personalized PageRank and SimRank problems that give provable guarantees of approximation and build space optimal data structures to answer arbitrary on-line user queries. Experiments over 80M pages showed that for the personalized PageRank problem rounded dynamic programming performs remarkably well in practice both in terms of precomputation time, database size and the quality of approximation.

An interesting open question is whether our techniques can be extended to approximate other properties of Markov chains over massive graphs, e.g. the hitting time. Another important area of future work is to thoroughly evaluate the quality of the SimRank approximation algorithms. Finally we leave the existence of theoretically optimal algorithms for SimRank value and top list queries with parameter open.

REFERENCES

[1] Z. Bar-Yossef, R. Kumar, and D. Sivakumar. Sampling algorithms: Lower bounds and applications. Proc. of 33rd STOC, 2001.

[2] B. H. Bloom. Space/time trade-offs in hash coding with allowable errors. Commun. ACM, 13(7):422-426, 1970.

[3] P. Boldi and S. Vigna. The webgraph framework I: Compression techniques. Proc. of 13th WWW, pp. 595-602, 2004.

[4] A. Z. Broder and M. Mitzenmacher. Network applications of Bloom filters: A survey. Internet Mathematics, 1(4):485-509, 2005.

[5] M. Charikar, K. Chen, and M. Farach-Colton. Finding frequent items in data streams. Proc. of 29th ICALP, pp. 693-703, 2002.

[6] Y.-Y. Chen, Q. Gan, and T. Suel. Local methods for estimating PageRank values. Proc. of 12th CIKM, pp. 381-389, 2004.

[7] G. Cormode and S. Muthukrishnan. An improved data stream summary: The Count-Min sketch and its applications. Journal of Algorithms, 55(1):58-75, 2005.

[8] G. Cormode and S. Muthukrishnan. Summarizing and mining skewed data streams. Proc. of 5th SIAM Intl. Conf. on Data Mining, 2005.

[9] R. Fagin, R. Kumar, M. Mahdian, D. Sivakumar, and E. Vee. Comparing and aggregating rankings with ties. Proc. of 23rd PODS, 2004.

[10] D. Fogaras. Where to start browsing the web? Proc. of 3rd I2CS, Springer LNCS vol. 2877, pp. 65-79, 2003.

[11] D. Fogaras and B. R´cz. Towards scaling fully personalized PageRank. Proc. of 3rd WAW, pp. 105-117, 2004. Full version to appear in Internet Mathematics.

[12] D. Fogaras and B. Rácz. Scaling link-based similarity search. Proc. of 14th WWW, pp. 641-650, 2005. Full version available at www.ilab.sztaki.hu/websearch/Publications/.

[13] T. H. Haveliwala. Topic-sensitive PageRank: A context-sensitive ranking algorithm for web search. IEEE Transactions on Knowledge and Data Engineering, 15(4):784-796, 2003.

[14] M. R. Henzinger, P. Raghavan, and S. Rajagopalan. Computing on data streams. In External Memory Algorithms, DIMACS Book Series vol. 50., pp. 107-118. American Mathematical Society, 1999.

[15] J. Hirai, S. Raghavan, H. Garcia-Molina, and A. Paepcke. WebBase: A repository of web pages. Proc. of 9th WWW, pp. 277-293, 2000.

[16] G. Jeh and J. Widom. SimRank: A measure of structural-context similarity. Proc. of 8th SIGKDD, pp. 538-543, 2002.

[17] G. Jeh and J. Widom. Scaling personalized web search. Proc. of 12th WWW, pp. 271-279, 2003.

[18] S. Kamvar, T. H. Haveliwala, C. Manning, and G. Golub. Exploiting the block structure of the web for computing PageRank. Technical Report 2003-17, Stanford University, 2003.

[19] M. G. Kendall. Rank Correlation Methods. Hafner Publishing Co., New York, 1955.

[20] J. Kleinberg. Authoritative sources in a hyperlinked environment. Journal of the ACM, 46(5):604-632, 1999.

[21] E. Kushilevitz and N. Nisan. Communication Complexity. Cambridge University Press, 1997.

[22] F. McSherry. A uniform approach to accelerated PageRank computation. Proc. of 14th WWW, pp. 575-582, 2005.

[23] S. Muthukrishnan. Data streams: Algorithms and applications. Foundations and Trends in Theoretical Comp. Sci., 1(2), 2005.

[24] L. Page, S. Brin, R. Motwani, and T. Winograd. The PageRank citation ranking: Bringing order to the web. Technical Report 1999-66, Stanford University, 1998.

[25] C. R. Palmer, P. B. Gibbons, and C. Faloutsos. ANF: A fast and scalable tool for data mining in massive graphs. Proc. of 8th SIGKDD, pp. 81-90, 2002.

[26] P. K. C. Singitham, M. S. Mahabhashyam, and P. Raghavan. Efficiency-quality tradeoffs for vector score aggregation. Proc. of 30th VLDB, pp. 624-635, 2004.

[27] J. S. Vitter. External memory algorithms and data structures: Dealing with massive data. ACM Computing Surveys, 33(2):209-271, 2001.

Footnotes

... Analysis1
This work was supported by the Mobile Innovation Center, Hungary and Inter-University Center for Telecommunication and Informatics (ETIK). This is an abbreviated version of the full paper available at http:/www.ilab.sztaki.hu/websearch/Publications/.
... approach2
Over the publicly available Stanford WebBase graph [15] we computed an average over 1000 non-zeroes after 4 iterations; on average $ 24\%$ of all vertices are reached within $ k=15$ steps.
... operations3
We measure time in bit operations in order to better compare with bit optimal sketches as in Theorem 5.
... bound4
For the ease of presentation, we have ignored the issue of dangling nodes, ie. nodes with zero out-degree, throughout this paper. In the presence of dangling nodes the bound of Theorem 2 becomes $ 3\epsilon/c$.