Text Joins in an RDBMS for Web Data Integration

Luis Gravano

Columbia University

Panagiotis G. Ipeirotis

Columbia University

Nick Koudas

AT&T Labs-Research

Divesh Srivastava

AT&T Labs-Research

Abstract

The integration of data produced and collected across autonomous, heterogeneous web services is an increasingly important and challenging problem. Due to the lack of global identifiers, the same entity (e.g., a product) might have different textual representations across databases. Textual data is also often noisy because of transcription errors, incomplete information, and lack of standard formats. A fundamental task during data integration is matching of strings that refer to the same entity. In this paper, we adopt the widely used and established cosine similarity metric from the information retrieval field in order to identify potential string matches across web sources. We then use this similarity metric to characterize this key aspect of data integration as a join between relations on textual attributes, where the similarity of matches exceeds a specified threshold. Computing an exact answer to the text join can be expensive. For query processing efficiency, we propose a sampling-based join approximation strategy for execution in a standard, unmodified relational database management system (RDBMS), since more and more web sites are powered by RDBMSs with a web-based front end. We implement the join inside an RDBMS, using SQL queries, for scalability and robustness reasons. Finally, we present a detailed performance evaluation of an implementation of our algorithm within a commercial RDBMS, using real-life data sets. Our experimental results demonstrate the efficiency and accuracy of our techniques.

Keywords

indexing, data mining

Introduction

The integration of information from heterogeneous web sources is of central interest for applications such as catalog data integration and warehousing of web data (e.g., job advertisements and announcements). Such data is typically textual and can be obtained from disparate web sources in a variety of ways, including web site crawling and direct access to remote databases via web protocols. The integration of such web data exhibits many semantics- and performance-related challenges.

Consider a price-comparison web site, backed by a database, that combines product information from different vendor web sites and presents the results under a uniform interface to the user. In such a situation, one cannot assume the existence of global identifiers (i.e., unique keys) for products across the autonomous vendor web sites. This raises a fundamental problem: different vendors may use different names to describe the same product. For example, a vendor might list a hard disk as ``Western Digital 120Gb 7200 rpm,'' while another might refer to the same disk as ``Western Digiral HDD 120Gb'' (due to a spelling mistake) or even as ``WD 120Gb 7200rpm'' (using an abbreviation). A simple equality comparison on product names will not properly identify these descriptions as referring to the same entity. This could result in the same product entity from different vendors being treated as separate products, defeating the purpose of the price-comparison web site. To effectively address the integration problem, one needs to match multiple textual descriptions, accounting for:


or combinations thereof.

Any attempt to address the integration problem has to specify a measure that effectively quantifies ``closeness'' or ``similarity'' between string attributes. Such a similarity metric can help establish that ``Microsoft Windows XP Professional'' and ``Windows XP Pro'' correspond to the same product across the web sites/databases, and that these are different from the ``Windows NT'' product. Many approaches to data integration use a text matching step, where similar textual entries are matched together as potential duplicates. Although text matching is an important component of such systems [1,21,23], little emphasis has been paid on the efficiency of this operation.

Once a text similarity metric is specified, there is a clear requirement for algorithms that process the data from the multiple sources to identify all pairs of strings (or sets of strings) that are sufficiently similar to each other. We refer to this operation as a text join. To perform such a text join on data originating at different web sites, we can utilize ``web services'' to fully download and materialize the data at a local relational database management system (RDBMS). Once this materialization has been performed, problems and inconsistencies can be handled locally via text join operations. It is desirable for scalability and effectiveness to fully utilize the RDBMS capabilities to execute such operations.

In this paper, we present techniques for performing text joins efficiently and robustly in an unmodified RDBMS. Our text joins rely on the cosine similarity metric [20], which has been successfully used in the past in the WHIRL system [4] for a similar data integration task. Our contributions include:


The remainder of this paper is organized as follows. Section 2 presents background and notation necessary for the rest of the discussion, and introduces a formal statement of our problem. Section 3 presents SQL statements to preprocess relational tables so that we can apply the sampling-based text join algorithm of Section 4. Then, Section 5 presents the implementation of the text join algorithm in SQL. A preliminary version of Sections 3 and 5 appears in [12]. Section 6 reports a detailed experimental evaluation of our techniques in terms of both accuracy and performance, and in comparison with other applicable approaches. Section 7 discusses the relative merits of alternative string similarity metrics. Section 8 reviews related work. Finally, Section 9 concludes the paper and discusses possible extensions of our work.


Background and Problem

In this section, we first provide notation and background for text joins, which we follow with a formal definition of the problem on which we focus in this paper.

We denote with $\Sigma^{*}$ the set of all strings over an alphabet $\Sigma$. Each string in $\Sigma^{*}$ can be decomposed into a collection of atomic ``entities'' that we generally refer to as tokens. What constitutes a token can be defined in a variety of ways. For example, the tokens of a string could simply be defined as the ``words'' delimited by special characters that are treated as ``separators'' (e.g., ` '). Alternatively, the tokens of a string could correspond to all of its $q$-grams, which are overlapping substrings of exactly $q$ consecutive characters, for a given $q$. Our forthcoming discussion treats the term token as generic, as the particular choice of token is orthogonal to the design of our algorithms. Later, in Section 6 we experiment with different token definitions, while in Section 7 we discuss the effect of token choice on the characteristics of the resulting similarity function.

Let $R_1$ and $R_2$ be two relations with the same or different attributes and schemas. To simplify our discussion and notation we assume, without loss of generality, that we assess similarity between the entire sets of attributes of $R_1$ and $R_2$. Our discussion extends to the case of arbitrary subsets of attributes in a straightforward way. Given tuples $t_1 \in R_1$ and $t_2 \in R_2$, we assume that the values of their attributes are drawn from $\Sigma^{*}$. We adopt the widely used vector-space retrieval model [20] from the information retrieval field to define the textual similarity between $t_1$ and $t_2$.

Let $D$ be the (arbitrarily ordered) set of all unique tokens present in all values of attributes of both $R_1$ and $R_2$. According to the vector-space retrieval model, we conceptually map each tuple $t \in R_i$ to a vector $v_t \in \Re^{\vert D\vert}$. The value of the $j$-th component $v_t(j)$ of $v_t$ is a real number that corresponds to the weight of the $j$-th token of $D$ in $v_t$. Drawing an analogy with information retrieval terminology, $D$ is the set of all terms and $v_t$ is a document weight vector.

Rather than developing new ways to define the weight vector $v_t$ for a tuple $t \in R_i$, we exploit an instance of the well-established tf.idf weighting scheme from the information retrieval field. (tf.idf stands for ``term frequency, inverse document frequency.'') Our choice is further supported by the fact that a variant of this general weighting scheme has been successfully used for our task by Cohen's WHIRL system [4]. Given a collection of documents $C$, a simple version of the tf.idf weight for a term $w$ and a document $d$ is defined as $\mathit{tf_w} \log(idf_w)$, where $\mathit{tf_w}$ is the number of times that $w$ appears in document $d$ and $idf_w$ is $\frac{\vert C\vert}{n_w}$, where $n_w$ is the number of documents in the collection $C$ that contain term $w$. The tf.idf weight for a term $w$ in a document is high if $w$ appears a large number of times in the document and $w$ is a sufficiently ``rare'' term in the collection (i.e., if $w$'s discriminatory power in the collection is potentially high). For example, for a collection of company names, relatively infrequent terms such as ``AT&T'' or ``IBM'' will have higher idf weights than more frequent terms such as ``Inc.''

For our problem, the relation tuples are our ``documents,'' and the tokens in the textual attribute of the tuples are our ``terms.'' Consider the $j$-th token $w$ in $D$ and a tuple $t$ from relation $R_i$. Then $\mathit{tf_w}$ is the number of times that $w$ appears in $t$. Also, $idf_w$ is $\frac{\vert R_i\vert}{n_w}$, where $n_w$ is the total number of tuples in relation $R_i$ that contain token $w$. The tf.idf weight for token $w$ in tuple $t \in R_i$ is $v_t(j)=\mathit{tf_w}\log(idf_w)$. To simplify the computation of vector similarities, we normalize vector $v_t$ to unit length in the Euclidean space after we define it. The resulting weights correspond to the impact of the terms, as defined in [24]. Note that the weight vectors will tend to be extremely sparse for certain choices of tokens; we shall seek to utilize this sparseness in our proposed techniques.

Definition 1   Given tuples $t_1 \in R_1$ and $t_2 \in R_2$, let $v_{t_1}$ and $v_{t_2}$ be their corresponding normalized weight vectors and let $D$ be the set of all tokens in $R_1$ and $R_2$. The cosine similarity (or just similarity, for brevity) of $v_{t_1}$ and $v_{t_2}$ is defined as $sim(v_{t_1}, v_{t_2}) = \sum_{j=1}^{\vert D\vert} v_{t_1}(j) v_{t_2}(j)$ .

Since vectors are normalized, this measure corresponds to the cosine of the angle between vectors $v_{t_1}$ and $v_{t_2}$, and has values between 0 and 1. The intuition behind this scheme is that the magnitude of a component of a vector expresses the relative ``importance'' of the corresponding token in the tuple represented by the vector. Intuitively, two vectors are similar if they share many important tokens. For example, the string ``ACME'' will be highly similar to ``ACME Inc,'' since the two strings differ only on the token ``Inc,'' which appears in many different tuples, and hence has low weight. On the other hand, the strings ``IBM Research'' and ``AT&T Research'' will have lower similarity as they share only one relatively common term.

The following join between relations $R_1$ and $R_2$ brings together the tuples from these relations that are ``sufficiently close'' to each other, according to a user-specified similarity threshold $\phi $:

Definition 2   Given two relations $R_1$ and $R_2$, together with a similarity threshold $0 < \phi \leq 1$, the text join $R_1 \widetilde{\Join}_{\phi}R_2$ returns all pairs of tuples $(t_1, t_2)$ such that $t_1 \in R_1$ and $t_2 \in R_2$, and $sim(v_{t_1}, v_{t_2})\geq \phi$.

The text join ``correlates'' two relations for a given similarity threshold $\phi $. It can be easily modified to correlate arbitrary subsets of attributes of the relations. In this paper, we address the problem of computing the text join of two relations efficiently and within an unmodified RDBMS:

Problem 1   Given two relations $R_1$ and $R_2$, together with a similarity threshold $0 < \phi \leq 1$, we want to efficiently compute (an approximation of) the text join $R_1 \widetilde{\Join}_{\phi}R_2$ using ``vanilla'' SQL in an unmodified RDBMS.

In the sequel, we first describe our methodology for deriving, in a preprocessing step, the vectors corresponding to each tuple of relations $R_1$ and $R_2$ using relational operations and representations. We then present a sampling-based solution for efficiently computing the text join of the two relations using standard SQL in an RDBMS.


Tuple Weight Vectors

In this section, we describe how we define auxiliary relations to represent tuple weight vectors, which we later use in our purely-SQL text join approximation strategy.

As in Section 2, assume that we want to compute the text join $R_1 \widetilde{\Join}_{\phi}R_2$ of two relations $R_1$ and $R_2$. $D$ is the ordered set of all the tokens that appear in $R_1$ and $R_2$. We use SQL expressions to create the weight vector associated with each tuple in the two relations. Since -for some choice of tokens- each tuple is expected to contain only a few of the tokens in $D$, the associated weight vector is sparse. We exploit this sparseness and represent the weight vectors by storing only the tokens with non-zero weight. Specifically, for a choice of tokens (e.g., words or $q$-grams), we create the following relations for a relation $R_i$:

Figure 1: Preprocessing SQL statements to create auxiliary relations for relation $R_i$.

\fbox{ \begin{tabular}{ll} \begin{minipage}[t]{3in} \begin{tabbing} {\tt INS... ...oken weights & (f) Dummy relation used to create \emph{RiIDF} \end{tabular} }

Given two relations $R_1$ and $R_2$, we can use the SQL statements in Figure 1 to generate relations R1Weights and R2Weights with a compact representation of the weight vector for the $R_1$ and $R_2$ tuples. Only the non-zero tf.idf weights are stored in these tables. Interestingly, RiWeights and RiSum are the only tables that need to be preserved for the computation of $R_1 \widetilde{\Join}_{\phi}R_2$ that we describe in the remainder of the paper: all other tables are just necessary to construct RiWeights and RiSum. The space overhead introduced by these tables is moderate. Since the size of RiSum is bounded by the size of RiWeights, we just analyze the space requirements for RiWeights.

Consider the case where $q$-grams are the tokens of choice. (As we will see, a good value is $q=3$.) Then each tuple $R_i.t_j$ of relation $R_i$ can contribute up to approximately $\vert R_i.t_j\vert$ $q$-grams to relation RiWeights, where $\vert R_i.t_j\vert$ is the number of characters in $R_i.t_j$. Furthermore, each tuple in RiWeights consists of a tuple id tid, the actual token (i.e., $q$-gram in this case), and its associated weight. Then, if $C$ bytes are needed to represent tid and weight, the total size of relation RiWeights will not exceed $\sum_{j=1}^{\vert R_i\vert} (C+q)\cdot \vert R_i.t_j\vert = (C+q)\cdot \sum_{j=1}^{\vert R_i\vert} \vert R_i.t_j\vert$ , which is a (small) constant times the size of the original table $R_i$. If words are used as the token of choice, then we have at most $\frac{\vert R_i.t_j\vert}{2}$ tokens per tuple in $R_i$. Also, to store the token attribute of RiWeights we need no more than one byte for each character in the $R_i.t_j$ tuples. Therefore, we can bound the size of RiWeights by $1+\frac{C}{2}$ times the size of $R_i$. Again, in this case the space overhead is linear in the size of the original relation $R_i$.

Given the relations R1Weights and R2Weights, a baseline approach [13,18] to compute $R_1 \widetilde{\Join}_{\phi}R_2$ is shown in Figure 2. This SQL statement performs the text join by computing the similarity of each pair of tuples and filtering out any pair with similarity less than the similarity threshold $\phi $. This approach produces an exact answer to $R_1 \widetilde{\Join}_{\phi}R_2$ for $\phi>0$. Unfortunately, as we will see in Section 6, finding an exact answer with this approach is prohibitively expensive, which motivates the sampling-based technique that we describe next.

Figure 2: Baseline approach for computing the exact value of $R_1 \widetilde{\Join}_{\phi}R_2$.

\fbox{ \begin{minipage}{2.7in} \begin{tabbing} {\tt SELECT    r1w.tid AS tid1... ...VING    SUM(r1w.weight*r2w.weight)$\geq \phi$} \end{tabbing} \end{minipage} }


Sampling-Based Text Joins

The result of $R_1 \widetilde{\Join}_{\phi}R_2$ only contains pairs of tuples from $R_1$ and $R_2$ with similarity $\phi $ or higher. Usually we are interested in high values for threshold $\phi $, which should result in only a few tuples from $R_2$ typically matching each tuple from $R_1$. The baseline approach in Figure 2, however, calculates the similarity of all pairs of tuples from $R_1$ and $R_2$ that share at least one token. As a result, this baseline approach is inefficient: most of the candidate tuple pairs that it considers do not make it to the final result of the text join. In this section, we describe a sampling-based technique [2] to execute text joins efficiently, drastically reducing the number of candidate tuple pairs that are considered during query processing.

The sampling-based technique relies on the following intuition: $R_1 \widetilde{\Join}_{\phi}R_2$ could be computed efficiently if, for each tuple $t_q$ of $R_1$, we managed to extract a sample from $R_2$ containing mostly tuples suspected to be highly similar to $t_q$. By ignoring the remaining (useless) tuples in $R_2$, we could approximate $R_1 \widetilde{\Join}_{\phi}R_2$ efficiently. The key challenge then is how to define a sampling strategy that leads to efficient text join executions while producing an accurate approximation of the exact query results. The discussion of the technique is organized as follows:


The sampling algorithm described in this section is an instance of the approximate matrix multiplication algorithm presented in [2], which computes an approximation of the product $A=A_1 \cdot \ldots \cdot A_n$, where each $A_i$ is a numeric matrix. (In our problem, $n=2$.) The actual matrix multiplication $A'=A_2 \cdot \ldots \cdot A_n$ happens during a preprocessing, off-line step. Then, the on-line part of the algorithm works by processing the matrix $A_1$ row by row.

Token-Weighted Sampling

Consider tuple $t_q \in R_1$ with its associated token weight vector $v_{t_q}$, and each tuple $t_i \in R_2$ with its associated token weight vector $v_{t_i}$. When $t_q$ is clear from the context, to simplify the notation we use $\sigma_i$ as shorthand for $sim(v_{t_q},v_{t_i})$. We extract a sample of $R_2$ tuples of size $S$ for $t_q$ as follows:

Let $C_i$ be the number of times that $t_i$ appears in the sample of size $S$. It follows that:

Theorem 1     The expected value of $\frac{C_i}{S} \cdot T_V(t_q)$ is $\sigma_i$.$\Box$

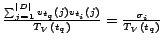The proof of this theorem follows from an argument similar to that in [2] and from the observation that the mean of the process that generates $C_i$ is $\frac{\sum_{j=1}^{\vert D\vert} v_{t_q}(j)v_{t_i}(j)}{T_V(t_q)} = \frac{\sigma_i}{T_V(t_q)}$ .

Theorem 1 establishes that, given a tuple $t_q \in R_1$, we can obtain a sample of size $S$ of tuples $t_i$ such that the frequency $C_i$ of tuple $t_i$ can be used to approximate $\sigma_i$. We can then report $\langle t_q, t_i \rangle$ as part of the answer of $R_1 \widetilde{\Join}_{\phi}R_2$ for each tuple $t_i \in R_2$ such that its estimated similarity with $t_q$ (i.e., its estimated $\sigma_i$) is $\phi'$ or larger, where $\phi' = (1-\epsilon)\phi$ is a threshold slightly lower1 than $\phi $.

Given $R_1$, $R_2$, and a threshold $\phi $, our discussion suggests the following strategy for the evaluation of the $R_1 \widetilde{\Join}_{\phi}R_2$ text join, in which we process one tuple $t_q \in R_1$ at a time:

This strategy guarantees that we can identify all pairs of tuples with similarity of at least $\phi $, with a desired probability, as long as we choose an appropriate sample size $S$. So far, the discussion has focused on obtaining an $R_2$ sample of size $S$ individually for each tuple $t_q \in R_1$. A naive implementation of this sampling strategy would then require a scan of relation $R_2$ for each tuple in $R_1$, which is clearly unacceptable in terms of performance. In the next section we describe how the sampling can be performed with only one sequential scan of relation $R_2$.


Practical Realization of Sampling

As discussed so far, the sampling strategy requires extracting a separate sample from $R_2$ for each tuple in $R_1$. This extraction of a potentially large set of independent samples from $R_2$ (i.e., one per $R_1$ tuple) is of course inefficient, since it would require a large number of scans of the $R_2$ table. In this section, we describe how to adapt the original sampling strategy so that it requires one single sample of $R_2$, following the ``presampling'' implementation in [2]. We then show how to use this sample to create an approximate answer for the text join $R_1 \widetilde{\Join}_{\phi}R_2$.

As we have seen in the previous section, for each tuple $t_q \in R_1$ we should sample a tuple $t_i$ from $R_2$ in a way that depends on the $v_{t_q}(j) \cdot v_{t_i}(j)$ values. Since these values are different for each tuple of $R_1$, a straightforward implementation of this sampling strategy requires multiple samples of relation $R_2$. Here we describe an alternative sampling strategy that requires just one sample of $R_2$: First, we sample $R_2$ using only the $v_{t_i}(j)$ weights from the tuples $t_i$ of $R_2$, to generate a single sample of $R_2$. Then, we use the single sample differently for each tuple $t_q$ of $R_1$. Intuitively, we ``weight'' the tuples in the sample according to the weights $v_{t_q}(j)$ of the $t_q$ tuples of $R_1$. In particular, for a desired sample size $S$ and a target similarity $\phi $, we realize the sampling-based text join $R_1 \widetilde{\Join}_{\phi}R_2$ in three steps:


  1. Sampling: We sample the tuple ids $i$ and the corresponding tokens from the vectors $v_{t_i}$ for each tuple $t_i \in R_2$. We sample each token $j$ from a vector $v_{t_i}$ with probability $\frac{v_{t_i}(j)}{Sum(j)}$. (We define $Sum(j)$ as the total weight of the $j$-th token in relation $R_2$, $Sum(j) = \sum_{i = 1}^{\vert R_2\vert} v_{t_i}(j)$. These weights are kept in relation R2Sum.) We perform $S$ trials, yielding approximately $S$ samples for each token $j$. We insert into $\mathit{R2Sample}$ tuples of the form $\langle i,j \rangle$ as many times as there were successful trials for the pair. Alternatively, we can create tuples of the form $\langle i,j,c \rangle$, where $c$ is the number of successful trials. This results in a compact representation of $\mathit{R2Sample}$, which is preferable in practice.


  2. Weighting: The Sampling step uses only the token weights from $R_2$ for the sampling, ignoring the weights of the tokens in the other relation, $R_1$. The cosine similarity, however, uses the products of the weights from both relations. During the Weighting step we use the token weights in the non-sampled relation to get estimates of the cosine similarity, as follows. For each $\mathit{R2Sample}$ tuple $\langle i,j \rangle$, with $c$ occurrences in the table, we compute the value $v_{t_q}(j) \cdot Sum(j) \cdot c$, which is an approximation of $v_{t_q}(j) \cdot v_{t_i}(j) \cdot S$. We add this value to a running counter that keeps the estimated similarity of the two tuples $t_q$ and $t_i$. The Weighting step thus departs from the strategy in [2], for efficiency reasons, in that we do not use sampling during the join processing.


  3. Thresholding: After the Weighting step, we include the tuple pair $\langle t_q, t_i \rangle$ in the final result only if its estimated similarity is no lower than the user-specified threshold (Section 4.1).


Such a sampling scheme identifies tuples with similarity no less than $\phi $ from $R_2$ for each tuple in $R_1$. By sampling $R_2$ only once, the sample will be correlated. As we verify experimentally in Section 6, this sample correlation has a negligible effect on the quality of the join approximation.

As presented, the join-approximation strategy is asymmetric in the sense that it uses tuples from one relation ($R_1$) to weight samples obtained from the other ($R_2$). The text join problem, as defined, is symmetric and does not distinguish or impose an ordering on the operands (relations). Hence, the execution of the text join $R_1 \widetilde{\Join}_{\phi}R_2$ naturally faces the problem of choosing which relation to sample. For a specific instance of the problem, we can break this asymmetry by executing the approximate join twice. Thus, we first sample from vectors of $R_2$ and use $R_1$ to weight the samples. Then, we sample from vectors of $R_1$ and use $R_2$ to weight the samples. Then, we take the union of these as our final result. We refer to this as a symmetric text join. We will evaluate this technique experimentally in Section 6.

In this section we have described how to approximate the text join $R_1 \widetilde{\Join}_{\phi}R_2$ by using weighted sampling. In the next section, we show how this approximate join can be completely implemented in a standard, unmodified RDBMS.


Sampling and Joining Tuple Vectors in SQL

We now describe our SQL implementation of the sampling-based join algorithm of Section 4.2. Section 5.1 addresses the Sampling step, while Section 5.2 focuses on the Weighting and Thresholding steps for the asymmetric versions of the join. Finally, Section 5.3 discusses the implementation of a symmetric version of the approximate join.


Implementing the Sampling Step in SQL

Figure 3: Creating an auxiliary relation that we sample to create RiSample(tid,token).

\fbox{ \begin{minipage}{2.7in} \begin{tabbing} {\tt SELECT  rw.tid, rw.token,... ...iSum rs}\ {\tt WHERE   rw.token = rs.token} \end{tabbing} \end{minipage} }

Given the $\mathit{RiWeights}$ relations, we now show how to implement the Sampling step of the text join approximation strategy (Section 4.2) in SQL. For a desired sample size $S$ and similarity threshold $\phi $, we create the auxiliary relation shown in Figure 3. As the SQL statement in the figure shows, we join the relations $\mathit{RiWeights}$ and $\mathit{RiSum}$ on the token attribute. The $P$ attribute for a tuple in the result is the probability $\mathit{\frac{RiWeights.weight}{RiSum.total}}$ with which we should pick this tuple (Section 4.2). Conceptually, for each tuple in the output of the query of Figure 3 we need to perform $S$ trials, picking each time the tuple with probability $P$. For each successful trial, we insert the corresponding tuple $\langle tid,token \rangle$ in a relation $\mathit{RiSample(tid,token)}$, preserving duplicates. The $S$ trials can be implemented in various ways. One (expensive) way to do this is as follows: We add ``AND P $\geq$ RAND()'' in the WHERE clause of the Figure 3 query, so that the execution of this query corresponds to one ``trial.'' Then, executing this query $S$ times and taking the union of the all results provides the desired answer. A more efficient alternative, which is what we implemented, is to open a cursor on the result of the query in Figure 3, read one tuple at a time, perform $S$ trials on each tuple, and then write back the result. Finally, a pure-SQL ``simulation'' of the Sampling step deterministically defines that each tuple will result in Round( $S \cdot \mathit{\frac{RiWeights.weight}{RiSum.total}}$) ``successes'' after $S$ trials, on average. This deterministic version of the query is shown in Figure 42. We have implemented and run experiments using the deterministic version, and obtained virtually the same performance as with the cursor-based implementation of sampling over the Figure 3 query. In the rest of the paper -to keep the discussion close to the probabilistic framework- we use the cursor-based approach for the Sampling step.

Figure 4: A deterministic version of the Sampling step, which results in a compact representation of RiSample.

\fbox{ \begin{minipage}{2.7in} \begin{tabbing} {\tt INSERT INTO RiSample(tid,... ...        ROUND($S$ * rw.weight/rs.total, 0)>0} \end{tabbing} \end{minipage} }


Implementing the Weighting and Thresholding Steps in SQL

Figure 5: Implementing the Weighting and Thresholding steps in SQL. This query corresponds to the asymmetric execution of the sampling-based text join, where we sample $R_2$ and weight the sample using $R_1$.

\fbox{ \begin{minipage}{2.5in} \begin{tabbing} {\tt SELECT   r1w.tid AS tid1,... ...sum.total/r1v.Tv) $\!\!\geq\! S*\phi'$/r1v.Tv} \end{tabbing} \end{minipage} }

Section 4.2 described the Weighting and Thresholding steps as two separate steps. In practice, we can combine them into one SQL statement, shown in Figure 5. The Weighting step is implemented by the SUM aggregate in the HAVING clause. We weight each tuple from the sample according to $\frac{R1Weights.weight \cdot R2Sum.total}{R1V.T_V}$, which corresponds to $\frac{v_{t_q}(j)\cdot Sum(j)}{T_V(t_q)}$ (see Section 4.2)3. Then, we can count the number of times that each particular tuple pair appears in the results (see GROUP BY clause). For each group, the result of the SUM is the number of times $C_i$ that a specific tuple pair appears in the candidate set. To implement the Thresholding step, we apply the count filter as a simple comparison in the HAVING clause: we check whether the frequency of a tuple pair at least matches the count threshold (i.e., $C_i > \frac{S}{T_V(t_q)}\phi^{'}$). The final output of this SQL operation is a set of tuple id pairs with expected similarity of at least $\phi $. The SQL statement in Figure 5 can be further simplified by completely eliminating the join with the $R1V$ relation. The $R1V.T_V$ values are used only in the HAVING clause, to divide both parts of the inequality. The result of the inequality is not affected by this division, hence the $R1V$ relation can be eliminated when combining the Weighting and the Thresholding step into one SQL statement.


Implementing a Symmetric Text Join Approximation in SQL

Figure 6: A symmetric sampling-based text join $R_1 \widetilde{\Join}_{\phi}R_2$.

\fbox{ \begin{scriptsize} \begin{minipage}{2.7in} \begin{tabbing} {\tt SELEC... ...G AVG(Ci) $\geq$ $S*\phi'$} \end{tabbing} \end{minipage} \end{scriptsize} }

Up to now we have described only an asymmetric text join approximation approach, in which we sample relation $R_2$ and weight the samples according to the tuples in $R_1$ (or vice versa). However, as we described in Section 4.2, the text join $R_1 \widetilde{\Join}_{\phi}R_2$ treats $R_1$ and $R_2$ symmetrically. To break the asymmetry of our sampling-based strategy, we execute the two different asymmetric approximations and report the union of their results, as shown in Figure 6. Note that a tuple pair $\langle tid1, tid2 \rangle$ that appears in the result of the two intervening asymmetric approximations needs high combined ``support'' to qualify in the final answer (see HAVING clause in Figure 64).

An additional strategy naturally suggests itself: Instead of executing the symmetric join algorithm by joining the samples with the original relations, we can just join the samples, ignoring the original relations. We sample each relation independently, join the samples, and then weight and threshold the output. We implement the Weighting step by weighting each tuple with $\frac{R1Sum.total}{R1V.T_V}\cdot \frac{R2Sum.total}{R2V.T_V}$ . The count threshold in this case becomes $C_i > \frac{S\cdot S}{T_V(t_q)\cdot T_V(t_i)}\phi^{'}$ (again the $T_V$ values can be eliminated from the SQL implementation if we combine the Weighting and the Thresholding steps). Figure 7 shows the SQL implementation of this version of the sampling-based text join.

Figure 7: A symmetric sampling-based text join $R_1 \widetilde{\Join}_{\phi}R_2$ involving only the relation samples.

\fbox{ \begin{minipage}{2.5in} \begin{tabbing} {\tt SELECT   r1s.tid AS tid1,... ...M(r1sum.total * r2sum.total) $\geq S*S*\phi'$} \end{tabbing} \end{minipage} }


Experimental Evaluation

We implemented the proposed SQL-based techniques and performed a thorough experimental evaluation in terms of both accuracy and performance in a commercial RDBMS. In Section 6.1, we describe the techniques that we compare and the data sets and metrics that we use for our experiments. Then, we report experimental results in Section 6.2.


Experimental Settings

We implemented the schema and the relations described in Section 3 in a commercial RDMBS, Microsoft SQL Server 2000, running on a multiprocessor machine with 2x2Ghz Xeon CPUs and with 2Gb of RAM. SQL Server was configured to potentially utilize the entire RAM as a buffer pool. We also compared our SQL solution against WHIRL, an alternative stand-alone technique, not available under Windows, using a PC with 2Gb of RAM, 2x1.8Ghz AMD Athlon CPUs and running Linux.

Data Sets: For our experiments, we used real data from an AT&T customer relationship database. We extracted from this database a random sample of 40,000 distinct attribute values of type string. We then split this sample into two data sets, $R_1$ and $R_2$. Data set $R_1$ contains about 14,000 strings, while data set $R_2$ contains about 26,000 strings. The average string length for $R_1$ is 19 characters and, on average, each string consists of 2.5 words. The average string length for $R_2$ is 21 characters and, on average, each string consists of 2.5 words. The length of the strings follows a close-to-Gaussian distribution for both data sets and is reported in Figure 8(a), while the size of $R_1 \widetilde{\Join}_{\phi}R_2$ for different similarity thresholds $\phi $ and token choices is reported in Figure 8(b). We briefly discuss experiments over other data sets later in this section.

Figure 8: Characteristics of the two data sets $R_1$ and $R_2$.
  \includegraphics[width=0.9\columnwidth]{figs/lengths.eps}  
  (a)
String lengths in data sets $R_1$ and $R_2$.
 
  \includegraphics[width=0.9\columnwidth]{figs/distances.eps}  
  (b)
The size of $R_1 \widetilde{\Join}_{\phi}R_2$ for different similarity thresholds and token choices.
 


Metrics: To evaluate the accuracy and completeness of our techniques we use the standard precision and recall metrics:

Definition 3   Consider two relations $R_1$ and $R_2$ and a user-specified similarity threshold $\phi $. Let $\mathit{Answer}_{\phi}$ be an approximate answer for text join $R_1 \widetilde{\Join}_{\phi}R_2$. Then, the precision and recall of $\mathit{Answer}_{\phi}$ with respect to $R_1 \widetilde{\Join}_{\phi}R_2$ are defined as:

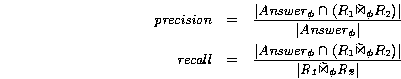
\begin{eqnarray}\html{eqn0} \mathit{precision} & = &\frac{\vert \mathit{Answer}... ...t}{\vert\mathit{R_1 \widetilde{\Join}_{\phi}R_2\vert}} \nonumber \end{eqnarray}


Precision and recall can take values in the 0-to-1 range. Precision measures the accuracy of the answer and indicates the fraction of tuples in the approximation of $R_1 \widetilde{\Join}_{\phi}R_2$ that are correct. In contrast, recall measures the completeness of the answer and indicates the fraction of the $R_1 \widetilde{\Join}_{\phi}R_2$ tuples that are captured in the approximation. We believe that recall is more important than precision. The returned answer can always be checked for false positives in a post-join step, while we cannot locate false negatives without re-running the text join algorithm.

Finally, to measure the efficiency of the algorithms, we measure the actual execution time of the text join for different techniques.

Choice of Tokens: We present experiments for different choices of tokens for the similarity computation. (Section 7 discusses the effect of the token choice on the resulting similarity function.) The token types that we consider in our experiments are:


The R1Weights table has 30,933 rows for Words, 268,458 rows for Q-grams with $q=3$, and 245,739 rows for Q-grams with $q=2$. For the R2Weights table, the corresponding numbers of rows are 61,715, 536,982, and 491,515. In Figure 8(b) we show the number of tuple pairs in the exact result of the text join $R_1 \widetilde{\Join}_{\phi}R_2$, for the different token choices and for different similarity thresholds $\phi $.

Techniques Compared: We compare the following algorithms for computing (an approximation of) $R_1 \widetilde{\Join}_{\phi}R_2$. All of these algorithms can be deployed completely within an RDBMS:


In addition, we also compare the SQL-based techniques against the stand-alone WHIRL system [4]. Given a similarity threshold $\phi $ and two relations $R_1$ and $R_2$, WHIRL computes the text join $R_1 \widetilde{\Join}_{\phi}R_2$. The fundamental difference with our techniques is that WHIRL is a separate application, not connected to any RDBMS. Initially, we attempted to run WHIRL over our data sets using its default settings. Unfortunately, during the computation of the $R_1 \widetilde{\Join}_{\phi}R_2$ join WHIRL ran out of memory. We then followed advice from WHIRL's author [5] and limited the maximum heap size 5 to produce an approximate answer for $R_1 \widetilde{\Join}_{\phi}R_2$. We measure the precision and recall of the WHIRL answers, in addition to the running time to produce them.

WHIRL natively supports only word tokenization, but not $q$-grams. To test WHIRL with $q$-grams, we adopted the following strategy: We generated all the $q$-grams of the strings in $R_1$ and $R_2$, and stored them as separate ``words.'' For example, the string ``ABC'' was transformed into ``$A AB BC C#'' for $q=2$. Then WHIRL used the transformed data set as if each $q$-gram were a separate word.

Besides the specific choice of tokens, three other main parameters affect the performance and accuracy of our techniques: the sample size $S$, the choice of the user-defined similarity threshold $\phi $, and the choice of the error margin $\epsilon $. We now experimentally study how these parameters affect the accuracy and efficiency of sampling-based text joins.


Experimental Results

Figure 9: Average precision and recall of different algorithms for (a) Words, (b) $Q$-grams with $q=2$, and (c) $Q$-grams with $q=3$, as a function of the similarity threshold $\phi $ (sample size $S=128$, $\epsilon =0$).
  \includegraphics[width=0.33\textwidth]{figs/sym-asym-words-precision.eps}   \includegraphics[width=0.33\textwidth]{figs/sym-asym-q2-precision.eps}   \includegraphics[width=0.33\textwidth]{figs/sym-asym-q3-precision.eps}  
  \includegraphics[width=0.33\textwidth]{figs/sym-asym-words-recall.eps}   \includegraphics[width=0.33\textwidth]{figs/sym-asym-q2-recall.eps}   \includegraphics[width=0.33\textwidth]{figs/sym-asym-q3-recall.eps}  
  (a) Words   (b) $Q$-grams with $q=2$   (c) $Q$-grams with $q=3$  


Comparing Different Techniques: Our first experiment evaluates the precision and recall achieved by the different versions of the sampling-based text joins and for WHIRL (Figure 9). For sampling-based joins, a sample size of $S=128$ is used (we present experiments for varying sample size $S$ below). Figure 9(a) presents the results for Words and Figures 9(b)(c) present the results for Q-grams, for $q=2$ and $q=3$. WHIRL has perfect precision (WHIRL computes the actual similarity of the tuple pairs), but it demonstrates very low recall for $Q$-grams. The low recall is, to some extent, a result of the small heap size that we had to use to allow WHIRL to handle our data sets. The sampling-based joins, on the other hand, perform better. For Words, they achieve recall higher than 0.8 for thresholds $\phi>0.1$, with precision above 0.7 for most cases when $\phi>0.2$ (with the exception of the $sR1sR2$ technique). WHIRL has comparable performance for $\phi>0.5$. For Q-grams with $q=3$, $sR1R2$ has recall around 0.4 across different similarity thresholds, with precision consistently above 0.7, outperforming WHIRL in terms of recall across all similarity thresholds, except for $\phi $=0.9. When $q=2$, none of the algorithms performs well. For the sampling-based text joins this is due to the small number of different tokens for $q=2$. By comparing the different versions of the sampling-based joins we can see that $sR1sR2$ performs worse than the other techniques in terms of precision and recall. Also, $R1sR2$ is always worse than $sR1R2$: Since $R_2$ is larger than $R_1$ and the sample size is constant, the sample of $R_1$ represents the $R_1$ contents better than the corresponding sample of $R_2$ does for $R_2$.

Figure 10: Average precision and recall of the symmetric version $R1R2$ of the algorithm, for different sample sizes $S$ and as a function of the similarity threshold $\phi $, for: (a) Words, (b) $Q$-grams with $q=2$, and (c) $Q$-grams with $q=3$ ($\epsilon =0$).
  \includegraphics[width=0.33\textwidth]{figs/sam-words-precision.eps}   \includegraphics[width=0.33\textwidth]{figs/sam-q2-precision.eps}   \includegraphics[width=0.33\textwidth]{figs/sam-q3-precision.eps}  
  \includegraphics[width=0.33\textwidth]{figs/sam-words-recall.eps}   \includegraphics[width=0.33\textwidth]{figs/sam-q2-recall.eps}   \includegraphics[width=0.33\textwidth]{figs/sam-q3-recall.eps}  
  (a) Words   (b) $Q$-grams with $q=2$   (c) $Q$-grams with $q=3$  


Effect of Sample Size $S$: The second set of experiments evaluates the effect of the sample size (Figure 10). As we increase the number of samples $S$ for each distinct token of the relation, more tuples are sampled and included in the final sample. This results in more matches in the final join, and, hence in higher recall. It is also interesting to observe the effect of the sample size for different token choices. The recall for $Q$-grams with $q=2$ is smaller than that for $Q$-grams with $q=3$ for a given sample size, which in turn is smaller than the recall for Words. Since we independently obtain a constant number of samples per distinct token, the higher the number of distinct tokens the more accurate the sampling is expected to be. This effect is visible in the recall plots of Figure 10. The sample size also affects precision. When we increase the sample size, precision generally increases. However, in specific cases we can observe that smaller sizes can in fact achieve higher precision. This happens because for a smaller sample size we may get an underestimate of the similarity value (e.g., estimated similarity 0.5 for real similarity 0.7). Underestimates do not have a negative effect on precision. However, an increase in the sample size might result in an overestimate of the similarity, even if the absolute estimation error is smaller (e.g., estimated similarity 0.8 for real similarity 0.7). Overestimates, though, affect precision negatively when the similarity threshold $\phi $ happens to be between the real and the (over)estimated similarity.

Effect of Error Margin $\epsilon $: As mentioned in Section 4.1, the threshold for count filter is $\frac{S}{T_V(t_q)}(1-\epsilon)\phi$. Different values of $\epsilon $ affect the precision and recall of the answer. Figure 11 shows how different choices of $\epsilon $ affect precision and recall. When we increase $\epsilon $, we lower the threshold for count filter and more tuple pairs are included in the answer. This, of course, increases recall, at the expense of precision: the tuple pairs included in the result have estimated similarity lower than the desired threshold $\phi $. The choice of $\epsilon $ is an ``editorial'' decision, and should be set to either favor recall or precision. As discussed above, we believe that higher recall is more important: the returned answer can always be checked for false positives in a post-join step, while we cannot locate false negatives without re-running the text join algorithm.

Figure 11: Average precision and recall of the $R1R2$ algorithm, for different similarity thresholds and different values of $\epsilon $ ($S=128$, $Q$-grams with $q=3$).
  \includegraphics[width=0.7\columnwidth]{figs/epsilon-q3-precision.eps}  
  \includegraphics[width=0.7\columnwidth]{figs/epsilon-q3-recall.eps}  


Figure 12: The execution time of the algorithms for different sample sizes and token choices.
  \includegraphics[width=0.36\textwidth]{figs/timing-words.eps}   \includegraphics[width=0.36\textwidth]{figs/timing-q3.eps}  
  (a) Words ($\phi=0.5$)   (b) $Q$-grams with $q=3$ ($\phi=0.5$)  
  \includegraphics[width=0.36\textwidth]{figs/timing-q2.eps}   \includegraphics[width=0.36\textwidth]{figs/timing-whirl.eps}  
  (c) $Q$-grams with $q=2$ ($\phi=0.5$)   (d) WHIRL  


Execution Time: To analyze efficiency, we measure the execution time of the different techniques. Our measurements do not include the preprocessing step to build the auxiliary tables in Figure 1: This preprocessing step is common to the baseline and all sampling-based text join approaches. This preprocessing step took less than one minute to process both relations $R_1$ and $R_2$ for Words, and about two minutes for $Q$-grams. Also, the time needed to create the RiSample relations is less than three seconds. For WHIRL we similarly do not include the time needed to export the relations from the RDBMS to a text file formatted as expected by WHIRL, the time needed to load the text files from disk, or the time needed to construct the inverted indexes6. The preprocessing time for WHIRL is about five seconds for Words and thirty seconds for $Q$-grams, which is smaller than for the sampling-based techniques: WHIRL keeps the data in main memory, while we keep the weights in materialized relations inside the RDBMS.

The Baseline technique (Figure 2) could only be run for Words. For $Q$-grams, SQL Server executed the Baseline query for approximately 24 hours, using more than 60Gb of temporary disk space, without producing any results. At that point we decided to stop the execution. Hence, we only report results for Words for the Baseline technique.

Figure 12(a) reports the execution time of sampling-based text join variations for Words, for different sample sizes. The execution time of the join did not change considerably for different similarity thresholds 7, and is consistently lower than that for Baseline. For example, for $S=64$, a sample size that results in high precision and recall (Figure 10(a)), $R1R2$ is more than 10 times faster than Baseline. The speedup is even higher for $sR1R2$ and $R1sR2$. Figures 12(b) and 12(c) report the execution time for $Q$-grams with $q=2$ and $q=3$. Surprisingly, $sR1sR2$, which joins only the two samples, is not faster than the other variations. For all choices of tokens, the symmetric version $R1R2$ has an associated execution time that is longer than the sum of the execution times of $sR1R2$ and $R1sR2$. This is expected, since $R1R2$ requires executing $sR1R2$ and $R1sR2$ to compute its answer. Finally, Figure 12(d) reports the execution time for WHIRL, for different similarity thresholds. (Note that WHIRL was run on a slightly slower machine; see Section 6.1.) For $Q$-grams with $q=3$, the execution time for WHIRL is roughly comparable to that of $sR1R2$ when $S=128$. For this setting $sR1R2$ has recall generally at or above 0.4, while WHIRL has recall above 0.4 only for similarity threshold $\phi \geq 0.8$. For Words, WHIRL is more efficient than the sampling-based techniques for high values of $S$, while WHIRL has significantly lower recall for low to moderate similarity thresholds (Figure 9(a)). For example, for $S=128$ sampling-based text joins have recall above 0.8 when $\phi>0.1$ and WHIRL has recall above 0.8 only when $\phi>0.5$.

Alternative Data Sets: We also ran experiments for five additional data set pairs, $T1$ through $T5$, using again real data from different AT&T customer databases. $T1$ consists of two relations with approximately 26,000 and 260,000 strings respectively. The respective numbers for the remaining pairs are: $T2$: 500 and 1,500 strings; $T3$: 26,000 and 1,500 strings; $T4$: 26,000 and 26,000 strings; and $T5$: 30,000 and 30,000 strings.

Most of the results (reported in Figures 13 and 14) are analogous to those for the data sets $R_1$ and $R_2$. The most striking difference is the extremely low recall for the data set $T5$ and similarity thresholds $\phi=0.7$ and $\phi=0.8$, for $Q$-grams with $q=3$ (Figure 13). This behavior is due to peculiarities of the $T5$ data set: $T5$ includes 7 variations of the string ``CompanyA $\ldots$''8 (4 variations in each relation) that appear in a total of 2,160 and 204 tuples in each relation, respectively. Any pair of such strings has real cosine similarity of at least 0.8. Hence the text join contains many identical tuple pairs with similarity of at least 0.8. Unfortunately, our algorithm gives an estimated similarity of around 0.6 for 5 of these pairs. This results in low recall for only 5 distinct tuple pairs that, however, account for approximately 300,000 tuples in the join, considerably hurting recall. Exactly the same problem appears with 50 distinct entries of the form ``CompanyB $\ldots$'' (25 in each relation) that appear in 3,750 tuples in each relation. These tuples, when joined, result in only 50 distinct tuple pairs in the text join with similarity above 0.8 that again account for 300,000 tuples in the join. Our algorithm underestimates their similarity, which results in low recall for similarity thresholds $\phi=0.7$ and $\phi=0.8$.

Figure 13: Average precision and recall of the $R1R2$ algorithm for the data sets $T1$ through $T5$, for different similarity thresholds ($\epsilon =0.1$, $S=128$, $Q$-grams with $q=3$).
  \includegraphics[width=0.7\columnwidth]{figs/alternativesets-precision.eps}  
  \includegraphics[width=0.7\columnwidth]{figs/alternativesets-recall.eps}  


Figure 14: Average precision and recall of the $R1R2$ algorithm for the data sets $T1$ through $T5$, for different similarity thresholds ($\epsilon =0.1$, $S=128$, Words).
  \includegraphics[width=0.7\columnwidth]{figs/alternativesets-precision-words.eps}  
  \includegraphics[width=0.7\columnwidth]{figs/alternativesets-recall-words.eps}  


In general, the sampling-based text joins, which are executed in an unmodified RDBMS, have efficiency comparable to WHIRL, when WHIRL has sufficient main memory available: WHIRL is a stand-alone application that implements a main-memory version of the $A^*$ algorithm. This algorithm requires keeping large search structures during processing; when main memory is not sufficiently large for a data set, WHIRL's recall suffers considerably. The $A^*$ strategy of WHIRL could be parallelized [5], but a detailed discussion of this is outside the scope of this paper. In contrast, our techniques are fully executed within RDBMSs, which are designed to handle large data volumes in an efficient and scalable way.


Different Similarity Functions

Section 6 studied the accuracy and efficiency of text join executions, for different token choices and for a distance metric based on tf.idf token weights (Section 2). We now compare this distance metric against string edit distance, especially in terms of the effectiveness of the metrics in helping data integration applications.


Table 1: Different similarity functions for data integration, and the types of string mismatches that they can capture.
  Similarity Function Mismatches Captured Mismatches not Captured  
  Edit distance Spelling errors, insertions and deletions of short words Variations of word order, insertions and deletions of long words  
  Block edit distance Spelling errors, insertions and deletions of short words, variations of word order Insertions and deletions of long words  
  Cosine similarity with words as tokens Insertions and deletions of common words, variations of word order Spelling errors  
  Cosine similarity with $q$-grams as tokens Spelling errors, insertions and deletions of short or common words, variations of word order -  

The edit distance [16] between two strings is the minimum number of edit operations (i.e., insertions, deletions, and substitutions) of single characters needed to transform the first string into the second. The edit distance metric works very well for capturing typographical errors. For example, the strings ``Computer Science'' and ``Computer Scince'' have edit distance one. Also edit distance can capture insertions of short words (e.g., ``Microsoft'' and ``Microsoft Co'' have edit distance three). Unfortunately, a small increase of the distance threshold can capture many false matches, especially for short strings. For example, the string ``IBM'' is within edit distance three of both ``ACM'' and ``IBM Co.''

The simple edit distance metric does not work well when the compared strings involve block moves (e.g., ``Computer Science Department'' and ``Department of Computer Science''). In this case, we can use block edit distance, a more general edit distance metric that allows for block moves as a basic edit operation. By allowing for block moves, the block edit distance can also capture word rearrangements. Finding the exact block edit distance of two strings is an NP-hard problem [17]. Block edit distance cannot capture all mismatches. Differences between records also occur due to insertions and deletions of common words. For example, ``KAR Corporation International'' and ``KAR Corporation'' have block edit distance 14. If we allow large edit distance thresholds to capture such mismatches, the answer will contain a large number of false positive matches.

The insertion and deletion of common words can be handled effectively with the cosine similarity metric that we have described in this paper if we use words as tokens. Common words, like ``International,'' have low idf weight. Hence, two strings are deemed similar when they share many identical words (i.e., with no spelling mistakes) that do not appear frequently in the relation. This metric also handles block moves naturally. The use of words as tokens in conjunction with the cosine similarity as distance metric was proposed by WHIRL [4]. Unfortunately, this similarity metric does not capture word spelling errors, especially if they are pervasive and affect many of the words in the strings. For example, the strings ``Compter Science Department'' and ``Deprtment of Computer Scence'' will have zero similarity under this metric.

Hence, we can see that (block) edit distance and cosine similarity with words serve complementary purposes. Edit distance handles spelling errors well (and possibly block moves as well), while the cosine similarity with words nicely handles block moves and insertions of words.

A similarity function that naturally combines the good properties of the two distance metrics is the cosine similarity with $q$-grams as tokens. A block move minimally affects the set of common $q$-grams of two strings, so the two strings ``Gateway Communications'' and ``Communications Gateway'' have high similarity under this metric. A related argument holds when there are spelling mistakes in these words. Hence, ``Gteway Communications'' and ``Comunications Gateway'' will also have high similarity under this metric despite the block move and the spelling errors in both words. Finally, this metric handles the insertion and deletion of words nicely. The string ``Gateway Communications'' matches with high similarity the string ``Communications Gateway International'' since the $q$-grams of the word ``International'' appear often in the relation and have low weight. Table 1 summarizes the qualitative properties of the distance functions that we have described in this section.

The choice of similarity function impacts the execution time of the associated text joins. The use of the cosine similarity with words leads to fast query executions as we have seen in Section 6. When we use $q$-grams, the execution time of the join increases considerably, resulting nevertheless in higher quality of results with matches that neither edit distance nor cosine similarity with words could have captured. Given the improved recall and precision of the sampling-based text join when $q=3$ (compared to the case where $q=2$), we believe that the cosine similarity metric with 3-grams can serve well for data integration applications. A more thorough study of the relative merits of the similarity metrics for different applications is a subject of interesting future work.


Related Work

Integrating data from various sources is a problem that has attracted significant attention in different research communities. Various measures have been adopted to assess similarity or closeness between collections of entities to identify approximate matches.

In the statistical literature, the problem is referred to as the record linkage problem [8,25]. In this body of work similarity is quantified via a probabilistic framework that is aimed at minimizing the probability of ``misclassification,'' i.e., declaring two entities as different when they are actually the same. Learning the probabilities involves a training and a validation phase that can be quite complex to realize in practice. The bulk of work in this direction has concentrated on the modeling aspect, however, as opposed to on performance related issues. The typical assumption is that records fit in memory and/or that evaluation of the cross product of two files (and sometimes its materialization) is viable. This is not true with very large data collections.

Approximate matching of strings is a problem of central interest for data integration and cleansing applications [9,11]. The problem of approximate string matching has attracted interest in the algorithms and combinatorial pattern matching communities [19] and commonly the string edit distance (with its numerous variants) is adopted for approximate string match quantification. Gravano et al. [11] presented a method to integrate approximate string match via edit distance into a database and realize it as SQL statements. They exploited a series of filters to speed join operations between string attributes using the edit distance as a join predicate. More specifically, this operation reports, for any string in an attribute of a relation $R_1$, all strings in an attribute of a relation $R_2$ that are within a given edit distance. Hernández and Stolfo [14] studied how to identify approximate duplicate records in large databases. Their approach relies on the ability to form a ``pseudo-key'' for each tuple by concatenating elements from its attributes. Then, sorting and band joins [6] on the pseudo keys can be used to identify approximate duplicates. Pseudo-key formation is an application-dependent operation that requires domain knowledge. Sarawagi and Bhamidipaty [21] describe an active learning algorithm for combining different similarity functions. The system is based on users to manually mark a small set of ``potential duplicates'' as real duplicates or not, and then uses these examples to optimize the combination function. Cohen and Richman [3] use clustering in conjunction with the cosine similarity metric to create clusters of potential duplicate entries.

The information retrieval field has produced approaches to speed up query execution that involve computation of the cosine similarity metric using inverted indexes [26]. A key idea is to exploit inverted indexes for fast computation of term weights. These techniques are of limited applicability for our approach: since we calculate and store the token weights during the preprocessing step of Section 3, we avoid the overhead of weight calculation during the join operation. However, we can apply some of these techniques to speedup the preprocessing step. Other optimizations described in [26] describe how to efficiently compute the document ``lengths'' to calculate the cosine similarity between documents. Since we use normalized weights, we do not have to calculate the document lengths on the fly. Additional optimizations, such as ``quantization of weights,'' [26] can be easily implemented inside a database system both for the baseline and for the sampling approach. Finally, some techniques also make special use of the available main memory to improve query-processing performance. These techniques are not compatible with our key objective of running the text joins in an unmodified RDBMS. Techniques that are based on the pruning of the inverted index [22,24] are close in spirit to our work, especially if we implement the sampling step using the ROUND function (Figure 4), which effectively prunes all the tokens with small weights.

Sampling has been utilized in a variety of tasks of database interest including data mining, estimation and optimization of queries, and query answering. A range of database vendors provide declarative interfaces that support a variety of sampling techniques inside the database engine [15]. Iceberg queries [7] utilize sampling for efficient answering of group-by queries. In particular, the techniques proposed by Fang et al. [7] utilize approximate counting techniques based on variants of hashing to efficiently estimate aggregate functions on groups of tuples.

Grossman et al. [13] present techniques for representing text documents and their associated term frequencies in relational tables, as well as for mapping boolean and vector-space queries into standard SQL queries. They also use a query-pruning technique, based on word frequencies, to speed up query execution. In this paper, we follow the same general approach of translating complex functionality not natively supported by a RDBMS into operations and queries that a RDBMS can optimize and execute efficiently. Grossman et al.'s technique can be adapted for our text join problem; we evaluate a version of this approach experimentally in Section 6.

Finally, the approximate matrix multiplication algorithm in [2] and Cohen's WHIRL system [4] are closest to our work, and have been discussed in Sections 4 and 6, respectively. In particular, Section 4 summarizes the strategy in [2] as applied to our problem.


Conclusions and Future Work

In this paper, we studied the problem of matching textual attributes that refer to the same entity. For this, we adopted the well established measure of cosine similarity over the vector-space retrieval model and proposed a SQL implementation of a sampling-based strategy to compute text joins in an unmodified RDBMS. Our algorithms are approximate, and we experimentally evaluated the accuracy/performance tradeoffs.

The work presented herein raises various issues for further study. As a notable example, conducting a thorough qualitative study of the properties of the different similarity functions for data integration applications is an interesting piece of future work.

Bibliography

1
R. Ananthakrishna, S. Chaudhuri, and V. Ganti.
Eliminating fuzzy duplicates in data warehouses.
In Proceedings of the 28th International Conference on Very Large Databases (VLDB 2002), 2002.
2
E. Cohen and D. D. Lewis.
Approximating matrix multiplication for pattern recognition tasks.
In Proceedings of the Eighth Annual ACM-SIAM Symposium on Discrete Algorithms (SODA 1997), pages 682-691, 1997.
3
W. Cohen and J. Richman.
Learning to match and cluster large high-dimensional data sets for data integration.
In The Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD-2002), 2002.
4
W. W. Cohen.
Integration of heterogeneous databases without common domains using queries based on textual similarity.
In Proceedings of the 1998 ACM SIGMOD International Conference on Management of Data (SIGMOD'98), pages 201-212, 1998.
5
W. W. Cohen.
Personal communication, 2002.
6
D. J. DeWitt, J. F. Naughton, and D. A. Schneider.
An evaluation of non-equijoin algorithms.
In Proceedings of the 17th International Conference on Very Large Databases (VLDB'91), pages 443-452, 1991.
7
M. Fang, N. Shivakumar, H. Garcia-Molina, R. Motwani, and J. D. Ullman.
Computing iceberg queries efficiently.
In Proceedings of the 24th International Conference on Very Large Databases (VLDB'98), pages 299-310, 1998.
8
I. P. Fellegi and A. B. Sunter.
A theory for record linkage.
Journal of the American Statistical Association, 64(328):1183-1210, Dec. 1969.
9
H. Galhardas, D. Florescu, D. Shasha, E. Simon, and C.-A. Saita.
Declarative data cleaning: Language, model, and algorithms.
In Proceedings of the 27th International Conference on Very Large Databases (VLDB 2001), pages 371-380, 2001.
10
L. Gravano, P. G. Ipeirotis, H. Jagadish, N. Koudas, S. Muthukrishnan, L. Pietarinen, and D. Srivastava.
Using $q$-grams in a DBMS for approximate string processing.
IEEE Data Engineering Bulletin, 24(4):28-34, Dec. 2001.
11
L. Gravano, P. G. Ipeirotis, H. Jagadish, N. Koudas, S. Muthukrishnan, and D. Srivastava.
Approximate string joins in a database (almost) for free.
In Proceedings of the 27th International Conference on Very Large Databases (VLDB 2001), pages 491-500, 2001.
12
L. Gravano, P. G. Ipeirotis, N. Koudas, and D. Srivastava.
Text joins for data cleansing and integration in an RDBMS (poster paper).
In Proceedings of the 19th IEEE International Conference on Data Engineering (ICDE 2003), 2003.
13
D. A. Grossman, O. Frieder, D. O. Holmes, and D. C. Roberts.
Integrating structured data and text: A relational approach.
Journal of the American Society for Information Science, 48(2):122-132, 1997.
14
M. A. Hernández and S. J. Stolfo.
The merge/purge problem for large databases.
In Proceedings of the 1995 ACM SIGMOD International Conference on Management of Data (SIGMOD'95), pages 127-138, 1995.
15
K. Kulkarni, A. Mozes, A. Witwoski, M. Zaharioudakis, and F. Zemke.
SQL extensions for sampling.
Technical Report IEC JTC1/SC32, ISO International Organization for Standardization, Data Management and Interchange WG3 Database Languages Working Group, Oct. 2001.
16
V. I. Levenshtein.
Binary codes capable of correcting deletions, insertions and reversals.
Doklady Akademii Nauk SSSR, 163(4):845-848, 1965.
Original in Russian - translation in Soviet Physics Doklady 10(8):707-710, 1966.
17
D. Lopresti and A. Tomkins.
Block edit models for approximate string matching.
Theoretical Computer Science, 181(1):159-179, 1997.
18
C. Lundquist, O. Frieder, D. O. Holmes, and D. A. Grossman.
A parallel relational database management system approach to relevance feedback in information retrieval.
Journal of the American Society for Information Science, 50(5):413-426, 1999.
19
G. Navarro.
A guided tour to approximate string matching.
ACM Computing Surveys, 33(1):31-88, 2001.
20
G. Salton and M. J. McGill.
Introduction to modern information retrieval.
McGraw-Hill, 1983.
21
S. Sarawagi and A. Bhamidipaty.
Interactive deduplication using active learning.
In The Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD-2002), 2002.
22
A. Soffer, D. Carmel, D. Cohen, R. Fagin, E. Farchi, M. Herscovici, and Y. S. Maarek.
Static index pruning for information retrieval systems.
In Proceedings of the 24th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, SIGIR 2001, pages 43-50, 2001.
23
S. Tejada, C. A. Knoblock, and S. Minton.
Learning domain-independent string transformation weights for high accuracy object identification.
In The Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD-2002), 2002.
24
A. N. Vo, O. de Kretser, and A. Moffat.
Vector-space ranking with effective early termination.
In Proceedings of the 24th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, SIGIR 2001, pages 35-42, 2001.
25
W. E. Winkler.
Matching and record linkage.
In Business Survey Methods, pages 355-384. Wiley, 1995.
26
I. H. Witten, A. Moffat, and T. C. Bell.
Managing Gigabytes: Compressing and Indexing Documents and Images, second edition.
Morgan Kaufmann Publishing, May 1999.

Footnotes

... lower1
For all practical purposes, $\epsilon $ is treated as a positive constant less than 1.
...fig:sql-sam-round2
Note that this version of $\mathit{RiSample}$ uses the compact representation in which each tid-token pair has just one associated row.
...sec:practical)3
The SQL statement uses a relation R1V to implement the Weighting step, storing the $T_V(t_q)$ values for each tuple $t_q \in R_1$. As we show later, the R1V relation can be eliminated from the query, and is just shown here for clarity.
...fig:symmetricjoin4
Alternatively, we can use a different ``combination'' function instead of AVG, such as MAX or MIN.
... size  5
For Words the exact command was ``set maxheap 10000''. For $Q$-grams the command was ``set maxheap 8000''. This was the maximum heap size that allowed our $Q$-grams experiments to finish using WHIRL.
... indexes6
We used the command ``index $\langle\mathit{relation}\rangle$'' to force WHIRL to create the inverted lists before the join computation [5].
... thresholds  7
The results in Figure 12 were computed for similarity threshold $\phi=0.5$; the execution times for other values of $\phi $ are not significantly different from those for $\phi=0.5$.
...''8
For privacy reasons, we do not report the real name of the company.

Panagiotis G. Ipeirotis 2003-03-05