3

The EigenTrust Algorithm for Reputation Management in P2P Networks

Sepandar D. Kamvar
Stanford University
Mario T. Schlosser
Stanford University
Hector Garcia-Molina
Stanford University

hector@db.stanford.edu

Copyright is held by the author/owner(s).
WWW2003, May 20-24, 2003, Budapest, Hungary.
ACM 1-58113-680-3/03/0005.

Abstract:

Peer-to-peer file-sharing networks are currently receiving much attention as a means of sharing and distributing information. However, as recent experience shows, the anonymous, open nature of these networks offers an almost ideal environment for the spread of self-replicating inauthentic files.

We describe an algorithm to decrease the number of downloads of inauthentic files in a peer-to-peer file-sharing network that assigns each peer a unique global trust value, based on the peer's history of uploads. We present a distributed and secure method to compute global trust values, based on Power iteration. By having peers use these global trust values to choose the peers from whom they download, the network effectively identifies malicious peers and isolates them from the network.

In simulations, this reputation system, called EigenTrust, has been shown to significantly decrease the number of inauthentic files on the network, even under a variety of conditions where malicious peers cooperate in an attempt to deliberately subvert the system.

C.2.4Computer-Communication NetworksDistributed Systems[Distributed applications]H.3.3Information SystemsInformation Storage and Retrieval[Selection]H.2.7Information SystemsDatabase Management[Security, integrity and protection]

Algorithms,Performance,Theory

Introduction

Peer-to-peer file-sharing networks have many benefits over standard client-server approaches to data distribution, including improved robustness, scalability, and diversity of available data. However, the open and anonymous nature of these networks leads to a complete lack of accountability for the content a peer puts on the network, opening the door to abuses of these networks by malicious peers.

Attacks by anonymous malicious peers have been observed on today's popular peer-to-peer networks. For example, malicious users have used these networks to introduce viruses such as the VBS.Gnutella worm, which spreads by making a copy of itself in a peer's Gnutella program directory, then modifying the Gnutella.ini file to allow sharing of .vbs files [19]. Far more common have been inauthentic file attacks, wherein malicious peers respond to virtually any query providing ``decoy files'' that are tampered with or do not work.

It has been suggested that the future development of P2P systems will depend largely on the availability of novel methods for ensuring that peers obtain reliable information on the quality of resources they are receiving [6]. In this context, attempting to identify malicious peers that provide inauthentic files is superior to attempting to identify inauthentic files themselves, since malicious peers can easily generate a virtually unlimited number of inauthentic files if they are not banned from participating in the network. We present such a method wherein each peer $ i$ is assigned a unique global trust value that reflects the experiences of all peers in the network with peer $ i$. In our approach, all peers in the network participate in computing these values in a distributed and node-symmetric manner with minimal overhead on the network. Furthermore, we describe how to ensure the security of the computations, minimizing the probability that malicious peers in the system can lie to their own benefit. And finally, we show how to use these values to identify peers that provide material deemed inappropriate by the users of a peer-to-peer network, and effectively isolate them from the network.

Design Considerations

There are five issues that are important to address in any P2P reputation system.

  1. The system should be self-policing. That is, the shared ethics of the user population are defined and enforced by the peers themselves and not by some central authority.

  2. The system should maintain anonymity. That is, a peer's reputation should be associated with an opaque identifier (such as the peer's Gnutella username) rather than with an externally associated identity (such as a peer's IP address).

  3. The system should not assign any profit to newcomers. That is, reputation should be obtained by consistent good behavior through several transactions, and it should not be advantageous for malicious peers with poor reputations to continuously change their opaque identifiers to obtain newcomers status.

  4. The system should have minimal overhead in terms of computation, infrastructure, storage, and message complexity.

  5. The system should be robust to malicious collectives of peers who know one another and attempt to collectively subvert the system.

Reputation Systems

An important example of successful reputation management is the online auction system eBay [9]. In eBay's reputation system, buyers and sellers can rate each other after each transaction, and the overall reputation of a participant is the sum of these ratings over the last 6 months. This system relies on a centralized system to store and manage these ratings.

In a distributed environment, peers may still rate each other after each transaction, as in the eBay system. For example, each time peer $ i$ downloads a file from peer $ j$, it may rate the transaction as positive ($ tr(i,j)=1$) or negative ( $ tr(i,j)=-1$). Peer $ i$ may rate a download as negative, for example, if the file downloaded is inauthentic or tampered with, or if the download is interrupted. Like in the eBay model, we may define a local trust value $ s_{ij}$ as the sum of the ratings of the individual transactions that peer $ i$ has downloaded from peer $ j$: $ s_{ij}=\sum tr_{ij}$.

Equivalently, each peer $ i$ can store the number satisfactory transactions it has had with peer $ j$, $ sat(i,j)$ and the number of unsatisfactory transactions it has had with peer $ j$, $ unsat(i,j)$. Then, $ s_{ij}$ is defined:

$\displaystyle s_{ij}= sat(i,j) - unsat(i,j)$ (1)

Previous work in P2P reputation systems [6,1] has all been based on similar notions of local trust values. The challenge for reputation systems in a distributed environment is how to aggregate the local trust values $ s_{ij}$ without a centralized storage and management facility. While each of the previous systems cited above addresses this issue, each of the previous systems proposed suffers from one of two drawbacks. Either it aggregates the ratings of only a few peers and doesn't get a wide view about a peer's reputation, or it aggregates the ratings of all the peers and congests the network with system messages asking for each peer's local trust values at every query.

We present here a reputation system that aggregates the local trust values of all of the users in a natural manner, with minimal overhead in terms of message complexity. Our approach is based on the notion of transitive trust: A peer $ i$ will have a high opinion of those peers who have provided it authentic files. Moreover, peer $ i$ is likely to trust the opinions of those peers, since peers who are honest about the files they provide are also likely to be honest in reporting their local trust values.

We show that the idea of transitive trust leads to a system where global trust values correspond to the left principal eigenvector of a matrix of normalized local trust values. We show how to perform this eigenvector computation in a distributed manner with just a few lines of code, where the message complexity is provably bounded and empirically low. Most importantly, we show that this system is highly effective in decreasing the number of unsatisfactory downloads, even when up to 70% of the peers in the network form a malicious collective in an attempt to subvert the system.


EigenTrust

In this section, we describe the EigenTrust algorithm. In EigenTrust, the global reputation of each peer $ i$ is given by the local trust values assigned to peer $ i$ by other peers, weighted by the global reputations of the assigning peers. In Section 4.1, we show how to normalize the local trust values in a manner that leads to an elegant probabilistic interpretation and an efficient algorithm for aggregating these values. In Section 4.2, we discuss how to aggregate the normalized trust values in a sensible manner. In Section 4.3, we discuss the probabilistic interpretation of the local and global trust values. In Section 4.4 through Section 4.6, we present an algorithm for computing the global trust values.


Normalizing Local Trust Values

In order to aggregate local trust values, it is necessary to normalize them in some manner. Otherwise, malicious peers can assign arbitrarily high local trust values to other malicious peers, and arbitrarily low local trust values to good peers, easily subverting the system. We define a normalized local trust value, $ c_{ij}$, as follows:

$\displaystyle c_{ij}=\frac{\max(s_{ij},0)}{\sum_j \max(s_{ij},0)}$ (2)

This ensures that all values will be between 0 and 1. (Notice that if $ \sum_j \max(s_{ij})=0$, then $ c_{ij}$ is undefined. We address this case in Section 4.4.) There are some drawbacks to normalizing in this manner. For one, the normalized trust values do not distinguish between a peer with whom peer $ i$ did not interact and a peer with whom peer $ i$ has had poor experience. Also, these $ c_{ij}$ values are relative, and there is no absolute interpretation. That is, if $ c_{ij} = c_{ik}$, we know that peer $ j$ has the same reputation as peer $ k$ in the eyes of peer $ i$, but we don't know if both of them are very reputable, or if both of them are mediocre. However, we are still able to achieve substantially good results despite the drawbacks mentioned above. We choose to normalize the local trust values in this manner because it allows us to perform the computation that we describe below without renormalizing the global trust values at each iteration (which is prohibitively costly in a large distributed environment) and leads to an elegant probabilistic model.


Aggregating Local Trust Values

We wish to aggregate the normalized local trust values. A natural way to do this in a distributed environment is for peer $ i$ to ask its acquaintances about their opinions about other peers. It would make sense to weight their opinions by the trust peer $ i$ places in them:

$\displaystyle t_{ik}=\sum_j c_{ij} c_{jk}$ (3)

where $ t_{ik}$ represents the trust that peer $ i$ places in peer $ k$ based on asking his friends.

We can write this in matrix notation: If we define $ C$ to be the matrix $ [c_{ij}]$ and $ \vec{t_i}$ to be vector containing the values $ t_{ik}$, then $ \vec{t_i} = C^T\vec{c_i}$. (Note that $ \sum_j t_{ij} =1$ as desired.)

This is a useful way to have each peer gain a view of the network that is wider than his own experience. However, the trust values stored by peer $ i$ still reflect only the experience of peer $ i$ and his acquantainces. In order to get a wider view, peer $ i$ may wish to ask his friends' friends ( $ t = (C^T)^2c_i$). If he continues in this manner, ( $ t = (C^T)^nc_i$), he will have a complete view of the network after $ n =$ large iterations (under the assumptions that $ C$ is irreducible and aperiodic, which we guarantee in practice and address in Section 4.5).

Fortunately, if $ n$ is large, the trust vector $ \vec{t_i}$ will converge to the same vector for every peer i. Namely, it will converge to the left principal eigenvector of $ C$. In other words, $ \vec{t}$ is a global trust vector in this model. Its elements, $ t_j$, quantify how much trust the system as a whole places peer $ j$.


Probabilistic Interpretation

It is useful to note that there exists a straightforward probabilistic interpretation of this method, similar to the Random Surfer model of [12]. If an agent were searching for reputable peers, it can crawl the network using the following rule: at each peer $ i$, it will crawl to peer $ j$ with probability $ c_{ij}$. After crawling for a while in this manner, the agent is more likely to be at reputable peers than unreputable peers. The stationary distribution of the Markov chain defined by the normalized local trust matrix $ C$ is our global trust vector $ \vec{t}$.


Basic EigenTrust

In this section, we describe the basic EigenTrust algorithm, ignoring for now the distributed nature of the peer-to-peer network. That is, we assume that some central server knows all the $ c_{ij}$ values and performs the computation. In Section 4.6, we describe how the computation may be performed in a distributed environment.

We simply wish to compute $ \vec{t}=(C^T)^n\vec{e}$, for $ n =$large, where we define $ \vec{e}$ to be the $ m$-vector representing a uniform probability distribution over all $ m$ peers, $ e_i=1/m$. (In Section 4.2, we said we wish to compute $ \vec{t}=(C^T)^n\vec{c_i}$, where $ \vec{c_i}$ is the normalized local trust vector of some peer $ i$. However, since they both converge to the principal left eigenvector of $ C$, we may use $ \vec{e}$ instead.)

At the most basic level, the algorithm would proceed as in Algorithm 1.


\begin{algorithm} % latex2html id marker 116 [t] $\vec{t}^{(0)} = \vec{e}$\; \Re... ...\vert$\; } \caption{Simple non-distributed EigenTrust algorithm} \end{algorithm}


Practical Issues

There are three practical issues that are not addressed by this simple algorithm: a priori notions of trust, inactive peers, and malicious collectives.

A priori notions of trust. Often, there are some peers in the network that are known to be trustworthy. For example, the first few peers to join a network are often known to be trustworthy, since the designers and early users of a P2P network are likely to have less motivation to destroy the network they built. It would be useful to incorporate such notions of trust in a natural and seamless manner. We do this by defining some distribution $ \vec{p}$ over pre-trusted peers[*]. For example, if some set of peers $ P$ are known to be trusted, we may define $ p_i=1/\vert P\vert$ if $ i \in P$, and $ p_i=0$ otherwise.) We use this distribution $ \vec{p}$ in three ways. First of all, in the presence of malicious peers, $ \vec{t}=(C^T)^n\vec{p}$ will generally converge faster than $ \vec{t}=(C^T)^n\vec{e}$, so we use $ \vec{p}$ as our start vector. We describe the other two ways to use this distribution $ \vec{p}$ below.

Inactive Peers. If peer $ i$ doesn't download from anybody else, or if it assigns a zero score to all other peers, $ c_{ij}$ from Equation 1 will be undefined. In this case, we set $ c_{ij}=p_j$. So we redefine $ c_{ij}$ as:

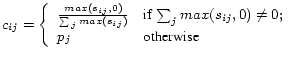$\displaystyle c_{ij} = \left\{ \begin{array}{ll} \frac{max(s_{ij},0)}{\sum_j ma... ...if $\sum_j max(s_{ij},0) \neq 0$};\\ p_j & \mbox{otherwise} \end{array} \right.$ (4)

That is, if peer $ i$ doesn't know anybody, or doesn't trust anybody, he will choose to trust the pre-trusted peers.

Malicious Collectives. In peer-to-peer networks, there is potential for malicious collectives to form [8]. A malicious collective is a group of malicious peers who know each other, who give each other high local trust values and give all other peers low local trust values in an attempt to subvert the system and gain high global trust values. We address this issue by taking

$\displaystyle \vec{t}^{(k+1)} = (1-a)C^T\vec{t}^{(k)} + a\vec{p}$ (5)

where $ a$ is some constant less than 1. This is equivalent to setting the opinion vector for all peers to be $ \vec{c_i}=(1-a)\vec{c_i} + a\vec{p}$, breaking collectives by having each peer place at least some trust in the peers $ P$ that are not part of a collective. Probabilistically, this is equivalent to saying that the agent that is crawling the network by the probabilistic model given in Section 4 is less likely to get stuck crawling a malicious collective, because at each step, he has a certain probability of crawling to a pre-trusted peer. Notice that this also makes the matrix $ C$ is irreducible and aperiodic, guaranteeing that the computation will converge.

The modified algorithm is given in Algorithm 2.
\begin{algorithm} % latex2html id marker 169 [t] \SetLine $\vec{t}^{(0)} = \vec{... ...+1)}-t^{(k)}\vert\vert$\; } \caption{Basic EigenTrust algorithm} \end{algorithm}

It should be emphasized that the pre-trusted peers are essential to this algorithm, as they guarantee convergence and break up malicious collectives. Therefore, the choice of pre-trusted peers is important. In particular, it is important that no pre-trusted peer be a member of a malicious collective. This would compromise the quality of the algorithm. To avoid this, the system may choose a very few number of pre-trusted peers (for example, the designers of the network). A thorough investigation of different methods of choosing pre-trusted peers is an interesting research area, but it is outside of the scope of this paper.


Distributed EigenTrust

Here, we present an algorithm where all peers in the network cooperate to compute and store the global trust vector, and the computation, storage, and message overhead for each peer are minimal.

In a distributed environment, the first challenge that arises is how to store $ C$ and $ \vec{t}$. In previous sections, we suggested that each peer could store its local trust vector $ \vec{c_i}$. Here, we also suggest that each peer store its own global trust value $ t_i$. (For presentation purposes, we ignore issues of security for the moment and allow peers to store their own trust values. We address issues of security in Section 5.)

In fact, each peer can compute its own global trust value:

$\displaystyle t_{i}^{(k+1)}=(1-a)(c_{1i}t_1^{(k)} + \ldots + c_{ni}t_n^{(k)}) + ap_i$ (6)

Inspection will show that this is the component-wise version of $ \vec{t}^{(k+1)}=(1-a)C^T\vec{t}^{(k)} + a\vec{p}$. Notice that, since peer $ i$ has had limited interaction with other peers, many of the components in equation 6 will be zero. This lends itself to the simple distributed algorithm shown in Algorithm 3.
\begin{algorithm} % latex2html id marker 207 [t] {\bf Definitions}: \begin{itemi... ..._{j}^{(k+1)}$\; } \} \caption{Distributed EigenTrust Algorithm.} \end{algorithm}
It is interesting to note two things here. First of all, only the pre-trusted peers need to know their $ p_i$. This means that pre-trusted peers may remain anonymous; nobody else needs to know that they are pre-trusted[*]. Therefore, the pre-trusted peers maintain anonymity as pre-trusted peers. (One may imagine that pre-trusted peers may be identified because they have high global trust values. However, simulations show that, while the pre-trusted peers have above average $ t_i$ values, they rarely have the highest values of $ t_i$.)

Secondly, in most P2P networks, each peer has limited interaction with other peers. There are two benefits to this. First, the computation $ t_{i}^{(k+1)} = (1-a)(c_{1i}t_1^{(k)} + c_{2i}t_2^{(k)} + \ldots + c_{ni}t_n^{(k)})+ ap_i$ is not intensive, since most $ c_{ji}$ are zero. Second, the number of messages passed is small, since $ A_i$ and $ B_i$ are small. In the case where a network is full of heavily active peers, we can enforce these benefits by limiting the number of local trust values $ c_{ij}$ that each peer can report.


Algorithm Complexity

The complexity of the algorithm is bounded in two ways. First, the algorithm converges fast: For a network of 1000 peers after 100 query cycles (refer to Section 7.1 for a description of how we simulate our system), Figure 1 depicts the residual $ \Vert t^{(k+1)} - t^{(k)}\Vert _1$. Clearly, the algorithm has converged after less than 10 iterations, i.e., the computed global trust values do not change significantly any more after a low number of iterations. In the distributed version of our algorithms, this corresponds to less than 10 exchanges of updated trust values among peers. The reason for the fast convergence of the EigenTrust algorithm is discussed in [10].

Figure 1: EigenTrust convergence
\begin{figure}\centering \psfig{file=convergence.ps,scale=0.75} \end{figure}

Second, we can specifically limit the number of local trust values that a peer reports. In the modified version of EigenTrust, each peer reports a subset of its total set of local trust values. Preliminary simulations have shown this scheme to perform comparably well as the algorithm presented here, where peers report all of their local trust values.


Secure EigenTrust

In the algorithm presented in the previous section, each peer $ i$ computes and reports its own trust value $ t_i$. Malicious peers can easily report false trust values, subverting the system.

We combat this by implementing two basic ideas. First, the current trust value of a peer must not be computed by and reside at the peer itself, where it can easily become subject to manipulation. Thus, we have a different peer in the network compute the trust value of a peer. Second, it will be in the interest of malicious peers to return wrong results when they are supposed to compute any peer's trust value. Therefore, the trust value of one peer in the network will be computed by more than one other peer.

In the secure version of the distributed trust algorithm, M peers (dubbed score managers of a peer $ i$) compute the trust value of a peer $ i$. If a peer needs the trust value of peer $ i$, it can query all M score managers for it. A majority vote on the trust value then settles conflicts arising from a number of malicious peers being among the score managers and presenting faulty trust values as opposed to the correct one presented by the non-malicious score managers.

To assign score managers, we use a distributed hash table (DHT), such as CAN [13] or Chord [18]. DHTs use a hash function to deterministically map keys such as file names into points in a logical coordinate space. At any time, the coordinate space is partitioned dynamically among the peers in the system such that every peer covers a region in the coordinate space. Peers are responsible for storing (key, value) pairs the keys of which are hashed into a point that is located within their region.

In our approach, a peer's score manager is located by hashing a unique ID of the peer, such as its IP address and TCP port, into a point in the DHT hash space. The peer which currently covers this point as part of its DHT region is appointed as the score manager of that peer. All peers in the system which know the unique ID of a peer can thus locate its score manager. We can modify our initial algorithm such that it can be executed by score managers.

Figure 2: Two-dimensional CAN hash space
\begin{figure}\centering \psfig{file=SecureTrustCAN.eps,scale=0.6}\end{figure}
As an example, consider the CAN in Figure 2. Peer 1's unique ID, $ ID_{1}$, is mapped into points covered by peers 2, 3 and 6, respectively, by hash functions $ h_{1}$, $ h_{2}$ and $ h_{3}$. Thus, these peers become peer 1's score managers.

To cope with the inherent dynamics of a P2P system, we rely on the robustness of a well-designed DHT. For example, when a score manager leaves the system, it passes on its state (i.e., trust values or ongoing trust computations) to its neighbor peer in the DHT coordinate space. DHTs also introduce replication of data to prevent loss of data (in this case, trust values) in case a score manager fails.


Algorithm Description

Here we describe the secure algorithm to compute a global trust vector. We will use these definitions: Each peer has a number $ M$ of score managers, whose DHT coordinates are determined by applying a set of one-way secure hash functions $ h_0, h_1, \ldots, h_{M-1}$ to the peer's unique identifier. $ pos_{i}$ are the coordinates of peer $ i$ in the hash space. Since each peer also acts as a score manager, it is assigned a set of daughters $ D_{i}$ - the set contains the indexes of peers whose trust value computation is covered by the peer. As a score manager, peer $ i$ also maintains the opinion vector $ c_d^i$ of its daughter peer $ d$ (where $ d \in D_{i}$) at some point in the algorithm. Also, peer $ i$ will learn $ A_{d}^{i}$ which is the set of peers which downloaded files from its daughter peer $ d$: It will receive trust assessments from these peers referring to its daughter peer $ d$. Finally, peer $ i$ will get to know the set $ B_{d}^{i}$ which denotes the set of peers which its daughter peer $ d$ downloaded files from: Upon kicking off a global trust value computation, its daughter peer $ d$ is supposed to submit its trust assessments on other peers to its score manager, providing the score manager with $ B_{d}^{i}$.


\begin{algorithm} % latex2html id marker 288 [H] \ForEach{peer~$i$}{ Submit loca... ...{jd}t_{j}^{(k+1)}$\; } } } \caption{Secure EigenTrust Algorithm} \end{algorithm}

Upsides of the secure algorithm in terms of increased security and reliability include:

Anonymity. It is not possible for a peer at a specific coordinate to find out the peer ID for whom it computes the trust values - hence malicious peers cannot increase the reputation of other malicious peers.

Randomization. Peers that enter the system cannot select at which coordinates in the hash space they want to be located (this should be a property of a well-designed DHT) - hence it is not possible for a peer to, for example, compute the hash value of its own ID and locate itself at precisely this position in the hash space to be able to compute its own trust value.

Redundancy. Several score managers compute the trust value for one peer. To assign several score managers to a peer, we use several multi-dimensional hash functions. Peers in the system still take over a particular region in the coordinate space, yet now there are several coordinate spaces, each of which is created by one multi-dimensional hash function. A peer's unique ID is thus mapped into a different point in every multi-dimensional hash space.

Discussion

A couple of points are important to note here. First, the issue of secure score management in P2P networks is an important problem, with implications for reputation management, incentive systems, and P2P micropayment schemes, among others. An extended discussion of secure score management in P2P networks, and various concrete score management schemes (including a variant of the one presented above), are given in [20]. The main contribution of this work is not in the secure score management scheme, but rather in the core EigenTrust algorithm. We discuss the secure score management scheme because some secure score management scheme is essential to the EigenTrust algorithm. However, it is important to note that the core EigenTrust algorithm may be used with many different secure score management schemes.

Second, the secure protocols proposed here and in [20] describe how to use large collections of entities to mitigate singular or group-based manipulation of the protocol. These protocols are not secured in the traditional sense; rather, we can show that the probability is small that a peer is able to get away with misreporting a score. This is discussed further in [20].


Using Global Trust Values

There are two clear ways to use these global trust values in a peer-to-peer system. The first is to isolate malicious peers from the network by biasing users to download from reputable peers. The second is to incent peers to share files by rewarding reputable peers.

Isolating Malicious Peers. When peer $ i$ issues a query, the system may use the trust values $ t_j$ to bias the user towards downloading from more reputable peers. One way to do this would be to have each peer download from the most highly trusted peer who responds to its query. However, such a policy leads to the most highly trusted peers being overloaded, as shown in Section 7. Furthermore, since reputation is built upon sharing authentic files, this policy does not enable new peers to build up reputation in the system.

A different strategy is to select the peers from whom to download probabilistically based on their trust values. In particular, we can make type probability that a peer will download a file from responding peer $ j$ be directly proportional to the trust value $ t_j$ of peer $ j$.

Such a policy limits the number of unsatisfactory downloads on the network, while balancing the load in the network and allowing newcomers to build reputation. The experiments in Section 7 validate this.

It should be noted here that peers may easily choose to bias their choice of download by a convex combination of the global trust values and their own local trust assessments of other peers (and use the trust values given by the vector $ \vec{t}_{\mathrm{personal}}=d\vec{t} + (1-d)\vec{c}$, where $ d$ is a constant between 0 and 1. This way, a peer can avoid downloading from a peer that has given it bad service, even if it gives the rest of the network good service.

Incenting Freeriders to Share. Secondly, the system may reward peers with high trust values. For example, reputable peers may be rewarded with increased connectivity to other reputable peers, or greater bandwidth. Rewarding highly trusted peers has a twofold effect. First, it gives users an incentive to share files, since a high global trust value may only be achieved by sharing authentic files. In the current Gnutella network, less than 7% of the peers are responsible for over 50% of the files, and as many as 25% of peers on the network share no files at all [16]. Incentives based on trust values should reduce the number of free riders on peer-to-peer networks. Some such incentives are discussed in [11].

Second, rewarding highly trusted peers gives non-malicious peers an incentive to delete inauthentic files that they may have accidentally downloaded from malicious peers, actively keeping the network tidy. This makes it more difficult for inauthentic files to replicate in the system.


Experiments

In this section, we will assess the performance of our scheme as compared to a P2P network where no reputation system is implemented. We shall demonstrate the scheme's performance under a variety of threat models.


Simulation

Our findings are based on simulations of a P2P network model which we shall explain briefly in the following.

Network model. We consider a typical P2P network: Interconnected, file-sharing peers are able to issue queries for files, peers can respond to queries, and files can be transferred between two peers to conclude a search process. When a query is issued by a peer, it is propagated by broadcast with hop-count horizon throughout the network (in the usual Gnutella way), peers which receive the query forward it and check if they are able to respond to it. We interconnect peers by a power-law network, a type of network prevalent in real-world P2P networks [15].

Node model. Our network consists of good nodes (normal nodes, participating in the network to download and upload files) and malicious nodes (adversarial nodes, participating in the network to undermine its performance). In our experiments, we consider different threat models, where a threat model describes the behavior of a malicious peer in the network. Threat models will be described in more detail later on. Note also that, based on the considerations in Section 4.5, some good nodes in the network are appointed as highly trusted nodes.

Content distribution model. Interactions between peers - i.e., which queries are issued and which queries are answered by given peers - are computed based on a probabilistic content distribution model. The detailed model will not be described here, it is presented in [17]. Briefly, peers are assumed to be interested in a subset of the total available content in the network, i.e., each peer initially picks a number of content categories and shares files only in these categories. Reference [7] has shown that files shared in a P2P network are often clustered by content categories. Also, we assume that within one content category files with different popularities exist, governed by a Zipf distribution. When our simulator generates a query, it does not generate a search string. Instead, it generates the category and rank (or popularity) of the file that will satisfy the query. The category and rank are based on Zipf distributions. Each peer that receives the query checks if it supports the category and if it shares the file. Files are assigned probabilistically to peers at initialization based on file popularity and the content categories the peer is interested (that is, peers are likely to share popular files, even if they have few files). The number of files shared by peers and other distributions used in the model are taken from measurements in real-world P2P networks [16].

Simulation execution. The simulation of a network proceeds in simulation cycles: Each simulation cycle is subdivided into a number of query cycles. In each query cycle, a peer $ i$ in the network may be actively issuing a query, inactive, or even down and not responding to queries passing by. Upon issuing a query, a peer waits for incoming responses, selects a download source among those nodes that responded and starts downloading the file. The latter two steps are repeated until a peer has properly received a good copy of the file that it has been looking for[*]. Upon the conclusion of each simulation cycle, the global trust value computation is kicked off. Statistics are collected at each node, in particular, we are interested in the number of authentic and inauthentic up- and downloads of each node. Each experiment is run several times and the results of all runs are averaged. We run an experiment until we see convergence to a steady state (to be defined in the descriptions of the experiments), initial transient states are excluded from the data.

The base settings that apply for most of the experiments are summarized in Table 1. The settings represent a fairly small network to make our simulations tractable. However, we have experimented with larger networks in some instances and our conclusions continue to hold. That is, schemes that do well in a small setting, do proportionately as well as the network is scaled up. Also note that our settings describe a pessimistic scenario with a powerful adversary: Malicious peers connect to the most highly connected peers when joining the network (see Section 7.3), they respond to the top 20% of queries received and thus have a large bandwidth, they are able to communicate among themselves in most of our threat models, and they make up a significant fraction of the network in most of our experiments. Yet, our experiments indicate that our scheme works well in this hostile a scenario, and thus will also work in less hostile environments.

Table 1: Simulation settings
Network # of good peers 60
  # of malicious peers 42
  # of pre-trusted peers 3
  # of initial neighbors of good peers 2
  # of initial neighbors of malicious peers 10
  # of initial neighbors of pre-trusted peers 10
  # Time-to-live for query messages 7
Content Distribution # of distinct files at good peer $ i$ file distribution in [16]
  set of content categories supported by good peer $ i$ Zipf distribution over 20 content categories
  # of distinct files at good peer $ i$ in category $ j$ uniform random distribution over peer $ i$'s
    total number of distinct files
  top % of queries for most popular categories and 20%
  files malicious peers respond to  
  top % of queries for most popular categories and 5%
  files pre-trusted peers respond to  
  % of time peer $ i$ is up and processing queries uniform random distribution over [0%, 100%]
  % of time pre-trusted peer $ i$ is up and processing 1
  queries  
  % of up-time good peer $ i$ issues queries uniform random distribution over [0%, 50%]
  % of up-time pre-trusted peer $ i$ issues queries 1
Peer Behavior % of download requests in which good peer $ i$ 5%
  returns inauthentic file  
  % of download requests in which malicious peer $ i$ 0% (varied in Section 7.3)
  returns inauthentic file  
  download source selection algorithm probabilistic algorithm (varied in Section 7.2)
  probability that peer with global trust value 0 is 10%
  selected as download source  
Simulation # of simulation cycles in one experiment 30
  # of query cycles in one simulation cycle 50
  # of experiments over which results are averaged 5



As metrics, we are particularly interested in the number of inauthentic file downloads versus the number of authentic file downloads: If the computed global trust values accurately reflect each peer's actual behavior, the number of inauthentic file downloads should be minimized.

Before we consider the strengths of our scheme in suppressing inauthentic downloads in a P2P network, we examine if it leads to unwanted load imbalance in the network. In the following section, we also give a precise definition on how we use global trust values in downloading files.


Load Distribution in a Trust-based
Network

Figure 3: Load distribution in a network using deterministic download source selection versus a non-trust based network. The load distribution is heavily skewed, peer 2 will eventually accumulate all reputation in the network.
\begin{figure}\centering \epsfig{file=loaddistrdet.eps, scale=0.27} \end{figure}

Figure 4: Load distribution in a network using probabilistic download source selection versus a non-trust based network. The load distribution does not deviate too much from the load distribution in a network based on random, non-trust based download source selection and is thus close to the natural load distribution in a normal Gnutella network.
\begin{figure}\centering \epsfig{file=loaddistrprob.eps, scale=0.27}\end{figure}
In P2P networks, a natural load distribution is established by peers with more content and higher bandwidth being able to respond to more queries and thus having a higher likelihood of being chosen as download source for a file transfer. In our scheme, a high global trust value of a peer additionally contributes to a peer's likelihood of being chosen as download source. Possibly, this might lead a peer into a vicious circle of accumulating reputation by responding to many queries, thus being chosen even more frequently as download source in the future, thus accumulating even more reputation. In a non-trust based system, this situation does not occur: From responding peers, a peer usually is randomly picked and selected as download source, somewhat balancing the load in the network. In the following, we are interested in integrating load-distributing randomization into our scheme. In the experiment in Figures 3 and 4, we study the load distribution performance of a network in which our scheme is activated. We consider two different trust-based algorithms for selecting download sources among peers responding to a query, a deterministic algorithm and a probabilistic algorithm.

If $ \{t_0, t_1, \ldots, t_{R-1}\}$ are the trust values of peers responding to a query, the deterministic and probabilistic algorithms proceed as follows.

Deterministic algorithm
Choose the peer with the highest trust value $ t_{max}$ among the peers responding to a query as download source.
Probabilistic algorithm
Choose peer $ i$ as download source with probability $ \frac{t_i}{\sum_{j=0}^{R} t_j}$. With a probability of 10%, select a peer $ j$ that has a trust value $ t_j = 0$.
If a download returns an inauthentic file, delete the peer from the list of responding peers and repeat the algorithm.

To give new peers in the network - which start with a global trust value of 0 - the chance of building up reputation, the probabilistic algorithm assigns a fixed 10% chance to download from the group of responding peers with trust value 0. Otherwise, new peers would maybe never be chosen as download source, depriving them of the chance to become a trusted member of the network. Based on our experience, a probability of 10% strikes a balance between granting malicious peers (which might also have a trust value of 0) too high a chance of uploading inauthentic files and allowing new peers to prove themselves as download sources of authentic files.

We compare these download source selection algorithms to a network where no reputation system is deployed, i.e., among peers responding to a query a peer is picked as download source entirely at random. We examine the load distribution in these networks. We do not assume the existence of any malicious peers in this experiment.[*]

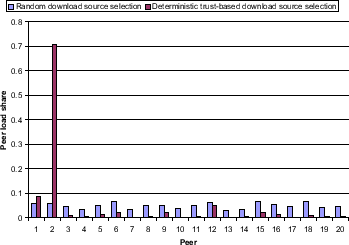
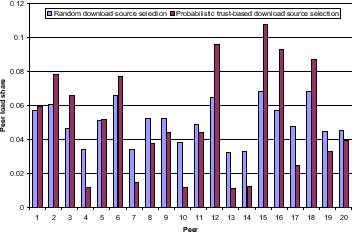
Setup. We simulate a network consisting of 20 good peers, no pre-trusted peers and no malicious peers. Other than that, the standard settings in Table 1 apply. After running queries on the system for 20 query cycles, the load distribution is measured in Figures 3 and 4: For each peer 1 - 20 in the network, we depict its load share, i.e., the fraction of its uploads after a full run of the experiment divided by the total number of uploads in the entire network. The load distribution in a network using the deterministic download source selection algorithm is compared to the load distribution in a network using no reputation system at all in Figure 3, whereas a system employing the probabilistic download source selection algorithm is compared to the non-trust based network in Figure 4.

Discussion. Always choosing the responding peer with the highest global trust value as download source leads to a vast load imbalance in the network: Popular peers do not stop accumulating trust value and gain further popularity. In Figure 3, peer 2 will eventually become the download source for virtually all queries that it is able to answer. Also note that in each experiment we ran another peer turned out to be the most trusted peer. Choosing download sources probabilistically yields only a slight deviation in terms of individual load share of each peer from the case where trust values are not used to select download sources among responding peers, therefore leading to a much better natural load distribution in the network. In Figure 4, peer 2 becomes the download source for 8% of all queries in the system, and many other peers participate in sharing the load, mainly determined by the number of and popularity of files the peers share. Our measurements also show that the efficiency in suppressing inauthentic downloads does not vary between the two approaches. Thus, for the remaining experiments we use the probabilistic peer selection algorithm.


Threat Models

We now evaluate the performance of our system in suppressing inauthentic downloads. We will consider several strategies of malicious peers to cause inauthentic uploads even when our scheme is activated. In short, malicious peers operating under threat model A simply try to upload inauthentic files and assign high trust values to any other malicious peer they get to interact with while participating in the network. In threat model B, malicious peers know each other upfront and deterministically give high local trust values to each other. In threat model C, malicious peers try to get some high local trust values from good peers by providing authentic files in some cases when selected as download sources. Under threat model D, one group of malicious peers in the network provides only authentic files and uses the reputation they gain to boost the trust values of another group of malicious peers that only provides inauthentic files.


Table 2: Threat models and associated experiments
Threat Model File Upload Behavior Local Trust Behavior Figure
A Always upload inauthentic files. Assign trust to peers which upload inauthentic files. 5
B Always upload inauthentic files. Assign trust to previously known malicious 6
    peer to form malicious collective.  
C Upload inauthentic files in $ f\%$ of all cases. Assign trust to previously known malicious 7, 8
    peer to form malicious collective.  
D Upload authentic files. Assign equal trust share to all type B nodes in the network. 9


We start our experiments considering the simplest threat model, where malicious peers are not initially aware of other malicious peers and simply upload inauthentic files.

Threat Model A. Individual Malicious Peers. Malicious peers always provide an inauthentic file when selected as download source. Malicious peers set their local trust values to be $ s_{ij} = inauth(j) - auth(j)$, i.e., malicious peers value inauthentic file downloads instead of authentic file downloads.

Setup. We simulate a network consisting of 63 good nodes, 3 of which are highly trusted nodes, applying the standard settings from Table 1. In each experiment, we add a number of malicious peers to the network such that malicious nodes make up between 0% and 70% of all nodes in the network. For each fraction in steps of 10% we run experiments and depict the results in Figure 5. Upon joining the network, malicious peers connect to the 10 most highly connected peers already in the network in order to receive as many queries travelling through the network as possible. In practice, P2P protocols such as the Gnutella protocol enable nodes to crawl the network in search of highly connected nodes. We run the experiments on a system where download sources are selected probabilistically based on our global trust values and on a system where download sources are chosen randomly from the set of peers responding to a query. Bars depict the fraction of inauthentic files downloaded in one simulation cycle versus the total number of files downloaded in the same period of time. The results are averaged over the last 10 query cycles in each experiment.

Figure 5: Reduction of inauthentic downloads by basing download source selection on global trust values in a network where independent malicious peers are present. Upon activation of our reputation scheme, the number of inauthentic downloads in the network is significantly decreased to around 10% of all downloads in the system, malicious peers in the network are virtually banned from uploading inauthentic files.
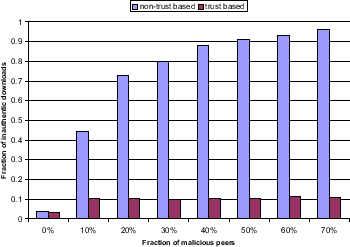\begin{figure}\centering \epsfig{file=ExpMaliciousPeersBasic.eps, scale=0.27}\end{figure}

Discussion. In the absence of a reputation system, malicious peers succeed in inflicting many inauthentic downloads on the network. Yet, if our scheme is activated, malicious peers receive high local trust values only from other malicious peers, and even that only occasionally - since malicious peers have to happen to get acquainted with each other through a file exchange. Because of their low trust values, malicious peers are rarely chosen as download source which minimizes the number of inauthentic file downloads in the network. We observed a 10% fraction of inauthentic downloads, mostly due to the fact that good nodes make mistakes once in a while and upload inauthentic files (for example, by not deleting a downloaded inauthentic file from their shared folders). Even if no malicious peers are present in the network, downloads are evaluated as inauthentic in 5% of all cases - this accounts for mistakes users make when creating and sharing a file, e.g., by providing the wrong meta-data or creating and sharing an unreadable file.

Note that, due to the fact that our current secure algorithm uses majority vote, a cooperating malicious collective that comprises over 40% of the network will be able to influence the assignment of global trust values values in the network during their computation. This is not represented in Figure 5, which assumes that the trust values are computed correctly. However, it is unlikely that over 40% of the peers in a network are in a single malicious collective, unless the malicious collective is a result of pseudospoofing (a.k.a. the Sybil attack [8]), where a single adversary initiates thousands of peers onto the network. This type of attack can be avoided by imposing a cost of entry into the network. For example, a peer wishing to enter the network may be required to solve a puzzle that a computer cannot solve [3,5]. Currently, YAHOO! requires a user to read some text from a JPEG file in order to open a YAHOO! Mail account.

Thus, in knowing that our scheme is present in a system, malicious peers know that they have to gain a somewhat high local trust value in order to be considered as download sources. Therefore, we will examine strategies on how malicious peers can increase their global trust value despite uploading inauthentic files.

Since malicious peers cannot expect to receive any high local trust values from non-malicious peers, they can try to increase their global trust value by teaming up as a malicious collective. In the experiment depicted in Figure 6, we vary the number of malicious peers in the network to assess their impact on the network's performance when they are aware of each other and form a malicious collective.

Threat Model B. Malicious Collectives. Malicious peers always provide an inauthentic file when selected as download source. Malicious peers form a malicious collective by assigning a single trust value of 1 to another malicious peer in the network. Precisely, if $ M$ denotes the set of malicious peers in the network, each $ peer_i \in M$ sets

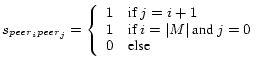
$\displaystyle s_{peer_{i}peer_{j}} = \left\{\begin{array}{rl}1 & \mbox{if }j = ... ...if }i = \vert M\vert \textrm{ and } j = 0 \\ 0 & \mbox{else}\end{array}\right. $

which resembles a malicious chain of mutual high local trust values. In terms of the probabilistic interpretation of our scheme, malicious peers form a collective out of which a random surfer or agent, once it has entered the collective, will not be able to escape, thus boosting the trust values of all peers in the collective.

Setup. We proceed exactly as in the previously described experiment, albeit with malicious nodes operating under threat model B. As shown in Figure 6, we run the experiments on a system where download sources are selected based on our global trust values and on a system where download sources are chosen randomly from the set of peers responding to a query.

Figure 6: Trust-based reduction of inauthentic downloads in a network where a fraction of peers forms a malicious collective and always uploads authentic files. Forming a malicious collective does not boost the trust values of malicious peers significantly, they are still virtually banned from uploading inauthentic files, similar to Figure 5.
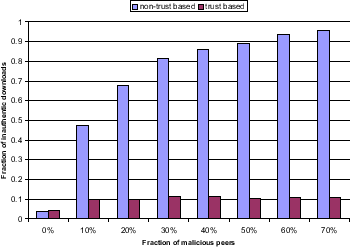\begin{figure}\centering \epsfig{file=ExpMaliciousPeersFraction.eps, scale=0.27}\end{figure}

Discussion. Our system performs well even if a majority of malicious peers is present in the network at a prominent place. The experiment clearly shows that forming a malicious collective does not decisively boost the global trust values of malicious peers: These peers are tagged with a low trust value and thus rarely chosen as download source. The system manages to break up malicious collectives through the presence of pre-trusted peers (see Section 4.4): If pre-trusted peers were not present in the network, forming a malicious collective in fact heavily boosts the trust values of malicious nodes. Under the presence of pre-trusted peers, the local trust values of malicious peers are significantly lower than those of good peers already after one simulation cycle. This minimizes the number of inauthentic downloads, and the numbers are virtually equal to the numbers in Figure 5 when peers do not form a malicious collective. For example, with 40% of all peers in a network being malicious, around 87% of all file downloads will end up in downloading an inauthentic version of the file in a normal, non-trusted network. Upon activation of our scheme, around 10% of all file downloads return an inauthentic file.

Forming a malicious collective obviously does not increase the global trust values of malicious peers sufficiently in order for them to have impact on the network. This leaves malicious peers with one choice: They have to increase their local trust values by receiving positive local trust values from at least some good and trusted peers in the network. In the experiment in Figure 7, we consider a strategy for malicious peers that is built on the idea that malicious peers try to get some positive local trust values from good peers.

Threat Model C. Malicious Collectives with Camoflouge. Malicious peers provide an inauthentic file in $ f$% of all cases when selected as download source. Malicious peers form a malicious collective as described above.

Setup. We simulate a network consisting of 53 good peers, 3 of which are pre-trusted peers, and 20 type C malicious peers applying the standard settings in Table 1. In each experiment, we apply a different setting of parameter $ f$ in threat model B such that the probability that malicious peers return an authentic file when selected as download source varies from 0% to 90%. We run experiments for each setting of parameter $ f$ in steps of 10%. Running the experiments on both a non-trust based system and on our system yields Figure 7. Bars depict the fraction of inauthentic files downloaded in one simulation cycle divided by the total number of files downloaded in the same period of time.

Figure 7: Trust-based reduction of inauthentic downloads in a network where a fraction of peers forms a malicious collective and returns authentic files with certain probabilities. When malicious peers partly provide authentic uploads, they receive more positive local trust values and will be selected as download sources more often, also increasing their chances to upload inauthentic files. Yet, uploading authentic files may be associated with a cost for malicious peers.
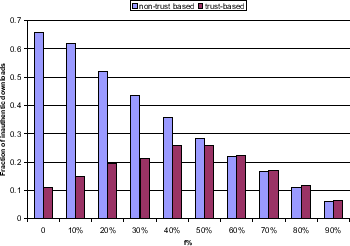\begin{figure}\centering \epsfig{file=ExpMimicry.eps, scale=0.27} \end{figure}

Figure 8: Inauthentic downloads versus authentic uploads provided by malicious peers with trust-based and non-trust based download source selection. When malicious peers provide authentic files in more than 20% of the cases when selected as download source, the increase in authentic files uploaded by malicious peers exceeds the increase in inauthentic downloads in the network, hence possibly coming at a higher cost than benefit for malicious peers.
\begin{figure}\centering \epsfig{file=ExpMimicryUpVsDownloads.eps, scale=0.27} \end{figure}

Discussion. Malicious peers that operate under threat model C attempt to gain positive local trust values from some peers in the network by sometimes providing authentic files. Thus, they will not be assigned zero trust values by all peers in the network since some peers will receive an authentic file from them. This in turn provides them with higher global trust values and more uploads - a fraction of which will be inauthentic. Figure 7 shows that malicious peers have maximum impact on the network when providing 50% authentic files: 28% of all download requests return inauthentic files then. However, this strategy comes at a cost for malicious peers: They have to provide some share of authentic files, which is undesirable for them. First of all, they try to prevent the exchange of authentic files on the network, and in this strategy they have to participate in it; second, maintaining a repository of authentic files requires a certain maintenance overhead.

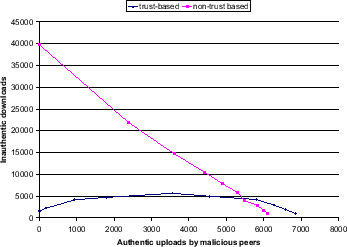
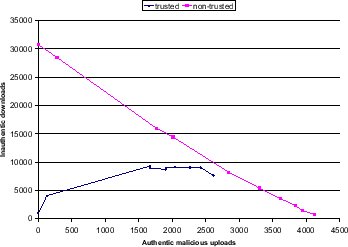
Figure 8 depicts the trade-off between authentic (horizontal axis) and inauthentic (vertical axis) downloads. Each scenario from Figure 7 is represented by one data point in Figure 8. For example, consider the fourth dark bar in Figure 7, corresponding to $ f=30\%$ and our reputation scheme in place. In this scenario, malicious peers provide 1850 authentic downloads and 5000 inauthentic ones in a particular run.[*] The value $ (1850, 5000)$ is plotted in Figure 8 as the fourth data point (left to right) on the lower curve, representing the case when our reputation scheme is used. The points on each curve represent increasing $ f$ values, from left to right.

In Figure 8, malicious nodes would like to operate in the upper left quadrant, providing a high number of inauthentic downloads, and a low number of authentic downloads. However, the file sharing mechanism in place constrains malicious nodes to operate along one of the curves shown. Without our reputation scheme (top curve), malicious nodes can set $ f$ to a small value and move to the upper left quadrant. On the other hand, with our scheme, malicious peers have no good choices. In particular, increasing $ f$ beyond 20% does not make much sense to malicious peers since the incremental authentic uploads they have to host outnumber the increase in inauthentic downloads. Moreover, for all settings of parameter $ f$ below 50%, malicious peers will lose all positive local trust values assigned by other peers in the long run - since on average they do provide more inauthentic than authentic files.

Notice that the lines cross at the lower right hand side. This does not show that the non-trust-based scheme works better for high values of $ f$. Rather, it shows that, when the trust-based scheme is implemented, malicious peers must upload more authentic files in order to be able to upload the same number of inauthentic files. This is the desired behavior.

The previous experiment has shown that malicious peers can increase their impact by partly concealing their malicious identity. Yet over time, their malicious identity will be uncovered and they lose their impact on the network. In the experiment in Figure 9, we consider a team effort strategy that malicious peers can use to work around this drawback. Two different types of malicious peers are present in the network: Malicious nodes of type B and of type D.

Threat Model D. Malicious Spies. Malicious peers answer 0.05% of the most popular queries and provide a good file when selected as download source. Malicious peers of type D assign trust values of 1 to all malicious nodes of type B in the network. Precisely, if $ M_B$ and $ M_D$ denote the set of malicious type B peers resp. type D peers in the network, each $ peer_i \in M_D$ sets

$\displaystyle s_{peer_{i}peer_{j}} = \left\{\begin{array}{rl}\frac{1}{\Vert M_B\Vert} & \mbox{if }peer_j \in M_B \\ 0 & \mbox{else}\end{array}\right. $

Figure 9: Inauthentic downloads versus authentic uploads provided by malicious peers with trust-based and non-trust based download source selection in a network populated by type D and type B peers. As with threat model C, malicious peers have to provide a number of authentic uploads in order to increase their global trust values. Yet, as compared to Figure 8, less authentic uploads by malicious peers are necessary to achieve equal numbers of inauthentic downloads in the network: 5000 inauthentic downloads cost 400 authentic uploads with this strategy as compared to more than 1000 authentic uploads with threat model C.
\begin{figure}\centering \epsfig{file=ExpCamouflageUpVsDownloads.eps, scale=0.27}\end{figure}

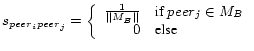
Setup. We simulate a network consisting of 63 good peers, 3 of which are pre-trusted peers, and 40 (39%) malicious peers, divided into two groups of malicious type B and type D peers. Otherwise, the standard settings from Table 1 apply. In each experiment, we consider a different number of type B and type D peers. Configurations considered are: I. 40 type B, 0 type D peers II. 39 type B, 1 type D peer III. 36 type B, 4 type D peers IV. 35 type B, 5 type D peers V. 30 type B, 10 type D peers VI. 25 type B, 15 type D peers VII. 20 type B, 20 type D peers VIII. 15 type B, 25 type D peers IX. 10 type B, 30 type D peers X. 5 type B, 35 type D peers. From left to right, we plot these data points in a graph that depicts the number of inauthentic file downloads versus the number of authentic file uploads provided by malicious peers, as in the previous experiment.

Discussion. Malicious peers establish an efficient division of labor in this scheme: Type D peers act as normal peers in the network and try to increase their global trust value, which they will in turn assign to malicious nodes of type B providing inauthentic files. The malicious nature of type D peers will not be uncovered over time since these peers do not provide inauthentic files - hence they can continue to increase the global local trust values of type B peers in the network. An interesting configuration for malicious peers would be configuration I: Malicious peers provide a fairly low number of authentic downloads (around 100), yet achieve almost the same number of inauthentic downloads in the network as in other configurations with a higher share of authentic downloads by malicious peers. In any configuration though, our scheme performs better than a system without trust-based download source selection. Also, this strategy would probably be the strategy of choice for malicious peers in order to attack a trust-based network: For example, by hosting 500 authentic file uploads in this strategy malicious peers achieve around 5000 inauthentic file downloads - as opposed to about 2500 inauthentic file downloads in the previous strategy, given the same effort on providing authentic uploads.

Other Threat Models

In this section, we discuss two slightly more nuanced threat models.

Threat Model E. Sybil Attack. An adversary initiates thousands of peers on the network. Each time one of the peers is selected for download, it sends an inauthentic file, after which it disconnected and replaced with a new peer identity.

Discussion. This threat scenario simply takes advantage of the fact that the fudge-factor that allows previously unknown users to obtain a reputation can be abused. Essentially, because there is no cost to create a new ID, the adversary can dominate that pool (with ghost identities). Because 10% of all traffic goes to the ``unknown'' pool, the malicious entity can behave arbitrarily without fear of losing reputation. To make matters worse, this kind of attack will prevent good peers from being able to garner a good reputation (they are so outnumbered that they will almost never be selected).

However, this threat scenario can be averted by imposing a cost to creating a new ID as discussed in Section 7.3 and [3]. For example, if a user must read the text off of a JPEG (or solve some other captcha [5]), it will be costly for a single adversary to create thousands of users.

Threat Model F. Virus-Disseminators. (variant of threat model C) A malicious peer sends one virus-laden (inauthentic) copy of a particular file every 100th request. At all other times, the authentic file is sent.

Discussion. This is a threat scenario that is not addressed by EigenTrust. EigenTrust greatly reduces - but does not completely eliminate - corrupt files on a P2P network. This is useful on a file-sharing network where executables are not shared. If executables are introduced that have potential to do great damage, then malicious peers can develop strategies to upload a few of them. But it should be noted that no reputation system to date claims to completely eliminate all corrupt files on a P2P network in an efficient manner. It should also be noted that the main problem on today's P2P networks is not the distribution of malicious executables (i.e. viruses), but rather the flooding of the network with inauthentic files. This is likely because today's P2P networks are mostly used to trade digital media, and relatively few users make use of these networks to share executables.

Related Work

An overview of many key issues in reputation management is given in [14]. Trust metrics on graphs have been presented in [2] and [4]. Beth et al. [4], also use the notion of transitive trust, but their approach is quite different from ours. Reputation systems for P2P networks in particular are presented in [6] and [1], and are largely based on notions similar to our local trust values. The contribution of this work is that it shows how to aggregate the local trust assessments of all peers in the network in an efficient, distributed manner that is robust to malicious peers.


Conclusion

We have presented a method to minimize the impact of malicious peers on the performance of a P2P system. The system computes a global trust value for a peer by calculating the left principal eigenvector of a matrix of normalized local trust values, thus taking into consideration the entire system's history with each single peer. We also show how to carry out the computations in a scalable and distributed manner. In P2P simulations, using these trust values to bias downloads has shown to reduce the number of inauthentic files on the network under a variety of threat scenarios. Furthermore, rewarding highly reputable peers with better quality of service incents non-malicious peers to share more files and to self-police their own file repository for inauthentic files.

Acknowledgements

We would like to thank the reviewers of this paper for detailed and insightful comments.

This paper is supported in part by the Research Collaboration between NTT Communication Science Laboratories, Nippon Telegraph and Telephone Corporation and CSLI, Stanford University (research project on Concept Bases for Lexical Acquisition and Intelligently Reasoning with Meaning).

Bibliography

1
K. Aberer and Z. Despotovic.
Managing Trust in a Peer-2-Peer Information System.
In Proceedings of the 10th International Conference on Information and Knowledge Management (ACM CIKM), New York, USA, 2001.

2
Advogato's Trust Metric (White Paper), http://www.advogato.org/trust-metric.html.

3
T. Aura, P. Nikander, and J. Leiwo.
Dos-resistant authentication with client puzzles.
In 8th International Workshop on Security Protocols, 2000.

4
T. Beth, M. Borcherding, and B. Klein.
Valuation of trust in open networks.
In Proc. 3rd European Symposium on Research in Computer Security - ESORICS '94, pages 3-18, 1994.

5
Captcha Project.
http://www.captcha.net.

6
F. Cornelli, E. Damiani, S. D. C. D. Vimercati, S. Paraboschi, and S. Samarati.
Choosing Reputable Servents in a P2P Network.
In Proceedings of the 11th World Wide Web Conference, Hawaii, USA, May 2002.

7
A. Crespo and H. Garcia-Molina.
Semantic Overlay Networks.
Submitted for publication 2002.

8
J. Douceur.
The Sybil Attack.
In First IPTPS, March 2002.

9
eBay website.
www.ebay.com.

10
T. H. Haveliwala and S. D. Kamvar.
The second eigenvalue of the google matrix.
Technical report, Stanford University, 2003.

11
S. D. Kamvar, M. T. Schlosser, and H. Garcia-Molina.
Incentives for Combatting Freeriding on P2P Networks.
Technical report, Stanford University, 2003.

12
L. Page, S. Brin, R. Motwani, and T. Winograd.
The PageRank Citation Ranking: Bringing Order to the Web.
Technical report, Stanford Digital Library Technologies Project, 1998.

13
S. Ratnasamy, P. Francis, M. Handley, R. Karp, and S. Shenker.
A scalable content-addressable network.
In Proceedings of ACM SIGCOMM, August 2001.

14
P. Resnick, R. Zeckhauser, E. Friedman, and K. Kuwabara.
Reputation Systems.
Communications of the ACM, 43(12):45-48, 2000.

15
M. Ripeanu and I. Foster.
Mapping the Gnutella Network - Macroscopic Properties of Large-scale P2P Networks and Implications for System Design.
In Internet Computing Journal 6(1), 2002.

16
S. Saroiu, P. K. Gummadi, and S. D. Gribble.
A Measurement Study of Peer-to-Peer File Sharing Systems.
In Proceedings of Multimedia Computing and Networking 2002 (MMCN '02), San Jose, CA, USA, January 2002.

17
M. T. Schlosser and S. D. Kamvar.
Simulating P2P Networks.
Technical report, Stanford University, 2003.

18
I. Stoica, R. Morris, D. Karger, M. F. Kaashoek, and H. Balakrishnan.
Chord: A scalable peer-to-peer lookup service for internet applications.
In Proceedings of the 2001 Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications, pages 149-160. ACM Press, 2001.

19
VBS.Gnutella Worm.
http://securityresponse.symantec.com/avcenter/venc/data/
vbs.gnutella.html.

20
B. Yang, S. D. Kamvar, and H. Garcia-Molina.
Secure Score Management for P2P Systems.
Technical report, Stanford University, 2003.

Footnotes

... peers[*]
The idea of pre-trusted peers is also used in [2], where the computation of the trust metric is performed relative to a ``seed'' of trusted accounts.
... pre-trusted[*]
Recall that, for the moment, we assume that peers are honest and may report their own trust values, including whether or not they are a pre-trusted peer. The secure version is presented in Section 5.
... for[*]
In Section 7.2 we will consider two different ways of choosing download sources from those nodes that respond to a query and compare their performance in one of our experiments.
... experiment.[*]
Malicious peers would not impact the load distribution among good peers since downloading peers keep trying until they have found an authentic copy of a file (assuming they have enough bandwidth to do so) - hence malicious peers would add inauthentic uploads to the network, but not change anything about the number of authentic uploads from good peers.
... run.[*]
More precisely, we run 30 query cycles, exclude the first 15 query cycles, and count the number of inauthentic and authentic downloads. We execute a second run, and add the numbers form both runs.

Sepandar Kamvar 2003-04-01