Introduction
An automated web agent visits the web, retrieving pages to perform some
processing such as indexing, archiving, site checking, etc., [3,11,24]. The robot uses page links in the
retrieved pages to discover new pages. All the pages on the web do not have
the same importance. For example, Le Louvre homepage is more important that
an unknown person's homepage. Page importance information is very valuable.
It is used by search engines to display results in the order of page
importance [11]. It is also useful
for guiding the refreshing and discovery of pages: important pages should be
refreshed more often![[*]](./p7-abiteboul-footnote.gif) and when
crawling for new pages, important pages have to be fetched first [6]. Following some ideas of [16], Page and Brin
proposed a notion of page importance based on the link structure of the web
[21]. This was then used by
Google with a remarkable success. Intuitively, a page is important if there
are many important pages pointing to it. This leads to a fixpoint computation
by repeatedly multiplying the matrix of links between pages with the vector
of the current estimate of page importance until the estimate is stable,
i.e., until a fixpoint is reached.
and when
crawling for new pages, important pages have to be fetched first [6]. Following some ideas of [16], Page and Brin
proposed a notion of page importance based on the link structure of the web
[21]. This was then used by
Google with a remarkable success. Intuitively, a page is important if there
are many important pages pointing to it. This leads to a fixpoint computation
by repeatedly multiplying the matrix of links between pages with the vector
of the current estimate of page importance until the estimate is stable,
i.e., until a fixpoint is reached.
The main issue in this context is the size
of the web, billions of pages [15,23]. Techniques have been
developed to compute page importance efficiently, e.g., [12]. The web is crawled and the
link matrix computed and stored. A version of the matrix is then frozen and
one separate process computes off-line page importance, which may take hours
or days for a very large graph. So, the core of the technology for the
off-line algorithms is fast sparse matrix multiplication (in particular by
extensive use of parallelism). This is a classical area, e.g., [25]. The algorithm we propose
computes the importance of pages on-line, with limited resources, while
crawling the web. It can be used to focus crawling to the most interesting
pages. Moreover, it is fully integrated in the crawling process, which is
important since acquiring web pages is the most costly part of the system.
Intuitively speaking, some ``cash'' is initially distributed to each page and
each page when it is crawled distributes its current cash equally to all
pages it points to. This fact is recorded in the history of the page. The
importance of a page is then obtained from the ``credit history'' of the
page. The intuition is that the flow of cash through a page is proportional
to its importance. It is essential to note that the importance we compute
does not assume anything about the selection of pages to visit. If a page
``waits'' for a while before being visited, it accumulates cash and has more
to distribute at the next visit. In Section 1 and 2, we present a formal model and we
prove the correctness of the algorithm.
In practice, the situation is more
complex. First, the ranking of result pages by a search engine should be
based on other factors than page importance. One may use criteria such as the
occurrences of the words from the query and their positions. These are
typically criteria from information retrieval [26] that have been used
extensively since the first generation of search engines, e.g. [3]. One may also want to bias the
ranking of answers based on the interest of users [19,22]. Such interesting
aspects are ignored here. On the other hand, we focus on another critical
aspect of page importance, the variations of importance when the web changes.
The web changes all the time. With the off-line algorithm, we need to restart
a computation. Although techniques can be used to take into account previous
computations, several costly iterations over the entire graph have to be
performed by the off-line algorithm. We show how to modify the on-line
algorithm to adapt to changes. Intuitively, this is achieved by taking into
account only a recent window of the history.
Several variants of the adaptive
on-line algorithm are presented. A distributed implementation of one of them
is actually used by the Xyleme crawlers [27,28]. The algorithms are described
using web terminology. However, the technique is applicable in a larger
setting to any graph. Furthermore, we believe that distributed versions of
the on-line algorithm could be useful in network applications when a link
matrix is distributed between various sites.
We also mention studies that we
conducted with librarians from the French national Library to decide if page
importance can be used to detect web sites that should be archived. More
precisely, we discuss some experiments and we detail how to use our system to
support new criteria of importance, such as site-based importance.
An
extended abstract of this work was published in [2]. A short and informal
presentation of the algorithm is given there. The formal presentation, the
details of the results as well as the discussion of the experiments are new.
The paper is organized as follows. We first present the model and in
particular, recall the definition of importance. In Section 2, we introduce the algorithm focusing
on static graphs. In Section 3,
we consider different crawling strategies and we move to dynamic graphs,
i.e., graphs that are continuously updated like the web. The following
section deals with implementation and discusses some experiments. The last
section is a conclusion.
Model
In this section, we present the formal model. Reading this section is not
mandatory for the comprehension of the rest of the paper.
We view the World Wide Web as a directed graph 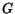 . The web
pages are the vertices. A link from one page to another form a directed edge.
We say that a directed graph
. The web
pages are the vertices. A link from one page to another form a directed edge.
We say that a directed graph 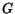 is connected if,
when directed edges are transformed into non directed edges, the resulting
graph is connected in the usual sense. A directed graph
is connected if,
when directed edges are transformed into non directed edges, the resulting
graph is connected in the usual sense. A directed graph 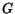 is said to be strongly connected if for all pair of vertices
is said to be strongly connected if for all pair of vertices 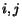 there exists a directed path going from
there exists a directed path going from  to
to  following the directed edges of
following the directed edges of 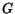 . A graph is said to be aperiodic if there exists a
. A graph is said to be aperiodic if there exists a 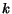 such that for all pair of vertices
such that for all pair of vertices 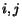 there
exists a directed path of length exactly
there
exists a directed path of length exactly 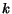 going from
going from
 to
to  following
the directed edges of
following
the directed edges of 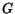 . Thus aperiodicity implies strong
connectedness. When the web graph is not connected, each connected components
may be considered separately.
Let
. Thus aperiodicity implies strong
connectedness. When the web graph is not connected, each connected components
may be considered separately.
Let 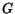 be any directed graph with
be any directed graph with 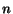 vertices. Fix an arbitrary ordering between the vertices.
vertices. Fix an arbitrary ordering between the vertices.  can be represented as a matrix
can be represented as a matrix ![$L[1..n, 1..n]$](./p7-abiteboul-img8.gif) such that:
such that:
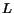 is nonnegative, i.e.
is nonnegative, i.e.
![$\forall i, \forall j, L[i,j]\geq0$](./p7-abiteboul-img10.gif)
![$L[i,j]>0$](./p7-abiteboul-img11.gif) if and only if there
is an edge from vertex
if and only if there
is an edge from vertex  to vertex
to vertex  .
.
There are several natural ways to encode a graph as a matrix,
depending on what property is needed afterwards. For instance,
Google [21,19] defines the out-degree ![$d[i]$](./p7-abiteboul-img12.gif) of a page as the number of outgoing links, and set
of a page as the number of outgoing links, and set ![$L[i,j]=1/d[i]$](./p7-abiteboul-img13.gif) if there is a link from
if there is a link from  to
to  . In [16], Kleinberg
proposes to set
. In [16], Kleinberg
proposes to set ![$K[i,j]=1$](./p7-abiteboul-img14.gif) if there is a link from
if there is a link from  to
to  , but then sets
, but then sets 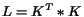 (where
(where 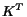 is the transpose of
matrix
is the transpose of
matrix 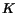 ).
The basic idea is to define the importance of a page in an inductive way and
then compute it using a fixpoint. If the graph contains
).
The basic idea is to define the importance of a page in an inductive way and
then compute it using a fixpoint. If the graph contains 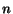 nodes, the importance is represented as a vector
nodes, the importance is represented as a vector 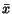 in a
in a 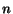 dimensional space. We consider three
examples, in which the importance is defined inductively by the equation
dimensional space. We consider three
examples, in which the importance is defined inductively by the equation
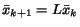 :
:
- If one decides that a page is important if it is pointed by important
pages. Then set
![$L[i,j]=1$](./p7-abiteboul-img20.gif) iff there is an edge
between
iff there is an edge
between  and
and  .
.
- A 'random walk' means that we browse the web by following one link at a
time, and all outgoing links of a page have equal probability to be
chosen. If one decides that a page importance is the probability to read
it during a 'random walk' on the web, then set
![$L[i,j]=1/d[i]$](./p7-abiteboul-img13.gif) iff there is a edge between
iff there is a edge between  and
and  . The random walk probabilities
correspond to the Markov chain with generator
. The random walk probabilities
correspond to the Markov chain with generator 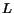 . This
definition of
. This
definition of 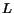 will result in the definition of
importance as in Google Pagerank.
will result in the definition of
importance as in Google Pagerank.
- If one decides that a page is important if it is pointed by important
pages or points to important pages. Then set
![$L[i,j]=1$](./p7-abiteboul-img20.gif) iff there is an edge between
iff there is an edge between  and
and  or an edge between
or an edge between  and
and
 . This is related to the work of
Kleinberg.
. This is related to the work of
Kleinberg.
In all cases, this leads to solving by induction an equation of the type
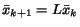 where
where 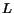 is a nonnegative matrix. This may be achieved by iterating over
is a nonnegative matrix. This may be achieved by iterating over
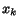 . Unfortunately, for obvious
modulus reasons, this is very likely to diverge or to converge to zero.
Observe that we are only interested in the relative importance of pages, not
their absolute importance. This means that only the direction of
. Unfortunately, for obvious
modulus reasons, this is very likely to diverge or to converge to zero.
Observe that we are only interested in the relative importance of pages, not
their absolute importance. This means that only the direction of 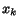 is relevant, not its norm. Thus it is more reasonable to
consider the following induction (equivalent for importance computation),
which uses the previous induction step but renormalizes after each step :
is relevant, not its norm. Thus it is more reasonable to
consider the following induction (equivalent for importance computation),
which uses the previous induction step but renormalizes after each step :
Computing the importance of the pages thus corresponds to finding a fixpoint
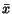 to
to 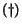 ,
each
,
each 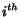 coordinate of
coordinate of 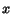 being the importance of page
being the importance of page  . By definition, such a
fixpoint is an eigenvector of
. By definition, such a
fixpoint is an eigenvector of 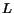 with a real positive
eigenvalue. If
with a real positive
eigenvalue. If 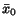 is a linear combination of
all eigenvector having a real positive eigenvalue then it is easy to see that
is a linear combination of
all eigenvector having a real positive eigenvalue then it is easy to see that
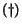 will converge to the
eigenspace corresponding to the dominant eigenvalue (i.e. which is
maximal). Thus, unless
will converge to the
eigenspace corresponding to the dominant eigenvalue (i.e. which is
maximal). Thus, unless 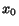 is not general enough (e.g. not
zero), the importance corresponds to an eigenvector of
is not general enough (e.g. not
zero), the importance corresponds to an eigenvector of 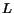 which eigenvalue is a positive real and which modulus is maximal among all
other eigenvalue. For each nonnegative matrix
which eigenvalue is a positive real and which modulus is maximal among all
other eigenvalue. For each nonnegative matrix 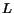 , there
always exists such an eigenvector (see Perron-Frobenius Theorem 1.1) but several problems may
occur:
, there
always exists such an eigenvector (see Perron-Frobenius Theorem 1.1) but several problems may
occur:
- There might be several solutions. This happens when the vector space
corresponding to the maximal eigenvalue has a dimension greater than
1.
- Even if there is a unique solution, the iteration
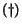 may not converge when the graph does not have some
desired properties.
may not converge when the graph does not have some
desired properties.
All these cases are completely characterized in the Theorem of
Perron-Frobenius that we give next.
In order to solve the convergence problem, Google [11] uses the following patch. Recall
that 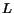 is defined in this case by
is defined in this case by ![$L[i,j]=1/d[i]$](./p7-abiteboul-img13.gif) iff there is an edge from
iff there is an edge from  to
to  . A new matrix
. A new matrix 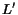 is defined such that
is defined such that
![$L'[i,j]=L[i,j] + \epsilon$](./p7-abiteboul-img31.gif) where
where 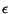 is a small real. Then the fixpoint is computed over
is a small real. Then the fixpoint is computed over 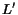 instead of
instead of 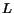 . Note that
. Note that 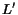 corresponds to a new graph
corresponds to a new graph 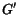 which is
which is
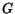 plus a ``small'' edge for any pair
plus a ``small'' edge for any pair
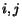 . Observe that the new graph
. Observe that the new graph 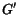 is strongly connected and aperiodic thus the convergence of
is strongly connected and aperiodic thus the convergence of
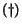 is guaranteed by Theorem 1.1. For each
is guaranteed by Theorem 1.1. For each 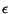 , this gives an importance vector
, this gives an importance vector
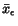 . It is not hard to
prove that when epsilon goes to zero,
. It is not hard to
prove that when epsilon goes to zero,
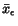 converges to an
eigenvector of
converges to an
eigenvector of 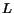 with a maximal real positive value.
Thus, for epsilon small enough,
with a maximal real positive value.
Thus, for epsilon small enough,
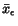 may be seen as a good
approximation of the importance. For some mysterious reason, Google sets
may be seen as a good
approximation of the importance. For some mysterious reason, Google sets 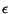 to
to 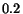
![[*]](./p7-abiteboul-footnote.gif) .
.
Another way to cope with the problem of convergence is to consider the
following convergence suite :
If 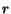 is the maximal eigenvalue of a
nonnegative matrix
is the maximal eigenvalue of a
nonnegative matrix 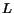 then
then 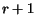 can be
shown to be the maximal eigenvalue of
can be
shown to be the maximal eigenvalue of 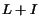 . Thus,
a solution
. Thus,
a solution 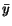 of
of 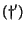 is
also a solution of
is
also a solution of 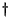 . If
. If 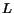 is
strongly connected then
is
strongly connected then 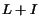 is aperiodic and thus
is aperiodic and thus 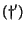 converges towards the importance. If
converges towards the importance. If 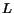 is not strongly connected there might be several linearly independent
eigenvector, but still it is easy to show that
is not strongly connected there might be several linearly independent
eigenvector, but still it is easy to show that 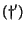 converges towards the projection of
converges towards the projection of 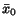 on
the eigenspace corresponding to all solutions.
The computation of page importance in a huge dynamic graph has recently
attracted a lot of attention because of the web, e.g., [18,21,19,22,9]. It is a major issue in practice
that the web is not strongly connected. For instance, in the bow tie
[4] vision of the web, the
in nodes do not branch back to the core of the web.
Although the same computation makes sense, it would yield a notion of
importance without the desired semantics. Intuitively, the random walk will
take us out of the core and would be ``trapped'' in pages that do not lead
back to the core (the ``rank sink'' according to [21]). So, pages in the core (e.g.,
the White House homepage) would have a null importance. Hence, enforcing
strong connectivity of the graph (by ``patches'') is more important from a
semantic point of view than for mathematical reasons. In a similar way to
Google, we enforce the strong connectivity of the graph by introducing
''small'' edges. More precisely, in our graph, each node points to a unique
virtual page. Conversely, this virtual page points to all other nodes.
Our algorithm computes the characteristic vector of
on
the eigenspace corresponding to all solutions.
The computation of page importance in a huge dynamic graph has recently
attracted a lot of attention because of the web, e.g., [18,21,19,22,9]. It is a major issue in practice
that the web is not strongly connected. For instance, in the bow tie
[4] vision of the web, the
in nodes do not branch back to the core of the web.
Although the same computation makes sense, it would yield a notion of
importance without the desired semantics. Intuitively, the random walk will
take us out of the core and would be ``trapped'' in pages that do not lead
back to the core (the ``rank sink'' according to [21]). So, pages in the core (e.g.,
the White House homepage) would have a null importance. Hence, enforcing
strong connectivity of the graph (by ``patches'') is more important from a
semantic point of view than for mathematical reasons. In a similar way to
Google, we enforce the strong connectivity of the graph by introducing
''small'' edges. More precisely, in our graph, each node points to a unique
virtual page. Conversely, this virtual page points to all other nodes.
Our algorithm computes the characteristic vector of 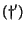 , and doesn't require any assumption on the graph. In
particular, it works for any link matrix
, and doesn't require any assumption on the graph. In
particular, it works for any link matrix 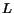 assuming
that
assuming
that 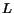 can be read line by line. More
precisely, for each page
can be read line by line. More
precisely, for each page  that is read, we use the values
that is read, we use the values ![$L[i,j]$](./p7-abiteboul-img42.gif) where
where ![$L[i,j]>0$](./p7-abiteboul-img11.gif) . For instance, in
Google's link matrix, these values corresponds to outgoing links (the pages
. For instance, in
Google's link matrix, these values corresponds to outgoing links (the pages
 pointed by page
pointed by page  ), which are known at little cost by parsing the HTML file. However, the
cost may be higher in some other cases (e.g., when
), which are known at little cost by parsing the HTML file. However, the
cost may be higher in some other cases (e.g., when ![$L[i,j]>0$](./p7-abiteboul-img11.gif) represents incoming links, we need to store and read
an index of links). In terms of convergences, the different cases are
characterized in a similar way as previously, e.g. if
represents incoming links, we need to store and read
an index of links). In terms of convergences, the different cases are
characterized in a similar way as previously, e.g. if 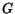 is strongly connected, the solution is unique and independent of the
initial vector
is strongly connected, the solution is unique and independent of the
initial vector 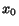 . Previous work is abundant in the
area of Markov chains and matrix fixpoint computations, e.g. [7] or [18]. In most cases,
infinite transition matrix are managed by increasing the size of a known
matrix block. Some works also consider a changing Web graph, e.g. an
incremental computation of approximations of page importance is proposed
in [5]. As far as we know,
our algorithm is new. In particular:
. Previous work is abundant in the
area of Markov chains and matrix fixpoint computations, e.g. [7] or [18]. In most cases,
infinite transition matrix are managed by increasing the size of a known
matrix block. Some works also consider a changing Web graph, e.g. an
incremental computation of approximations of page importance is proposed
in [5]. As far as we know,
our algorithm is new. In particular:
- it may start even when a (large) part of the matrix is still
unknown,
- it helps deciding which (new) part of the matrix should be acquired (or
updated),
- it is integrated in the crawling process,
- it works on-line even while the graph is being updated.
For instance, after crawling 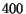 million pages on the
web, we have a relatively precise approximation of page importance for over
million pages on the
web, we have a relatively precise approximation of page importance for over
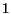 billion pages, i.e., even of parts
of the matrix that we do not know yet. A drawback for our algorithm is that
it is strictly tailored to the computational cost model of crawling the Web,
and in other cases converges slower than others after reading the same pages.
billion pages, i.e., even of parts
of the matrix that we do not know yet. A drawback for our algorithm is that
it is strictly tailored to the computational cost model of crawling the Web,
and in other cases converges slower than others after reading the same pages.
Static graphs: OPIC
We consider in this section the case of a static graph (no update). We
describe the algorithm for Google's link matrix 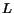 as defined
previously. It can be generalized to work for other link matrices. We present
the OPIC algorithm and show its correctness. We briefly discuss the
advantages of the technique over the off-line algorithm. We will consider
dynamic graphs in the next section.
For each page (each node in the graph), we keep two values. We call the first
cash. Initially, we distribute some cash to each node, e.g., if
there are
as defined
previously. It can be generalized to work for other link matrices. We present
the OPIC algorithm and show its correctness. We briefly discuss the
advantages of the technique over the off-line algorithm. We will consider
dynamic graphs in the next section.
For each page (each node in the graph), we keep two values. We call the first
cash. Initially, we distribute some cash to each node, e.g., if
there are 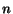 nodes, we distribute
nodes, we distribute 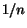 to each node. While the algorithm runs, the cash of a node
records the recent information discovered about the page, more precisely, the
sum of the cash obtained by the page since the last time it was crawled. We
also record the (credit) history of the page, the sum of the cash
obtained by the page since the start of the algorithm until the last time it
was crawled. The cash is typically stored in main memory whereas the history
may be stored on disk. When a page
to each node. While the algorithm runs, the cash of a node
records the recent information discovered about the page, more precisely, the
sum of the cash obtained by the page since the last time it was crawled. We
also record the (credit) history of the page, the sum of the cash
obtained by the page since the start of the algorithm until the last time it
was crawled. The cash is typically stored in main memory whereas the history
may be stored on disk. When a page  is retrieved by the web
agent, we know the pages it points to. In other words, we have at no cost the
outgoing links information for the retrieved page. We record its cash in the
history, i.e., we add it to the history. We also distribute this cash equally
between all pages it points to. We reset the cash of the page
is retrieved by the web
agent, we know the pages it points to. In other words, we have at no cost the
outgoing links information for the retrieved page. We record its cash in the
history, i.e., we add it to the history. We also distribute this cash equally
between all pages it points to. We reset the cash of the page  to 0. This happens each time we read a page. We will see that this
provides enough information to compute the importance of the page as used in
standard methods. We will consider in a further section how this may be
adapted to handle dynamic graphs.
We use two vectors
to 0. This happens each time we read a page. We will see that this
provides enough information to compute the importance of the page as used in
standard methods. We will consider in a further section how this may be
adapted to handle dynamic graphs.
We use two vectors ![$C[1..n]$](./p7-abiteboul-img46.gif) (the cash) and
(the cash) and ![$H[1..n]$](./p7-abiteboul-img47.gif) (the history). The initialization of
(the history). The initialization of  has no impact on the result. The history of a page is simply a number. A
more detailed history will be needed when we move to an adaptive version of
the algorithm. Let us assume that the history
has no impact on the result. The history of a page is simply a number. A
more detailed history will be needed when we move to an adaptive version of
the algorithm. Let us assume that the history  is stored
on disk and
is stored
on disk and 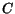 is kept in main memory. In order to
optimize the computation of
is kept in main memory. In order to
optimize the computation of
![$\vert H\vert=\sum_i{H[i]}$](./p7-abiteboul-img50.gif) , a variable
, a variable
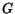 is introduced so that
is introduced so that 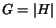 at each step. The algorithm is as follows:
at each step. The algorithm is as follows:
OPIC:
On-line Page Importance Computation
for each i let C[i] := 1/n ;
for each i let H[i] := 0 ;
let G:=0 ;
do forever
begin
choose some node i ;
%% each node is selected
%% infinitely often
H[i] += C[i];
%% single disk access per page
for each child j of i,
do C[j] += C[i]/out[i];
%% Distribution of cash
%% depends on L
G += C[i];
C[i] := 0 ;
end
At each step, an estimate of any page 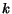 's
importance is
's
importance is
![$(H[k]+C[k]) / (G+1)$](./p7-abiteboul-img52.gif) . Note that the
algorithm does not impose any requirement on the order we visit the nodes of
the graph as long as each node is visited infinitely often (some minimal
fairness). This is essential since crawling policies are often
governed by considerations such as robots exclusion, politeness (avoid
rapid-firing), page change rate, focused crawling. As long as the cash of
children is stored in main memory, no disk access is necessary to update it.
At the time we visit a node (we crawl it), the list of its children is
available on the document itself and does not require disk access.
Each page has at least one child, thanks to the ``small'' edges that we
presented in previous Section (and that points to the virtual page). However,
for practical reasons, the cash of the virtual page is not distributed all at
once. This issue is in particular related to the discovery of new pages and
management of variable sized graphs that we consider later.
. Note that the
algorithm does not impose any requirement on the order we visit the nodes of
the graph as long as each node is visited infinitely often (some minimal
fairness). This is essential since crawling policies are often
governed by considerations such as robots exclusion, politeness (avoid
rapid-firing), page change rate, focused crawling. As long as the cash of
children is stored in main memory, no disk access is necessary to update it.
At the time we visit a node (we crawl it), the list of its children is
available on the document itself and does not require disk access.
Each page has at least one child, thanks to the ``small'' edges that we
presented in previous Section (and that points to the virtual page). However,
for practical reasons, the cash of the virtual page is not distributed all at
once. This issue is in particular related to the discovery of new pages and
management of variable sized graphs that we consider later.
Definition 2.1 We note
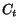
and
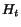
the values of vectors
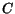
and
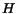
at the end of the
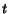
-th step of the algorithm. The vector
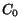
denotes
the value of vector
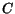
at initialization (all entries are
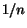
). Let
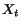
be
defined by:
i.e.,
One can prove that:
Theorem 2.1 Assuming the graph is connected, when
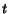
goes to infinity,
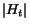
goes to
infinity and
and
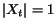
. Thus the vector
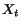
converges to the vector of
importance, i.e.,
To prove this theorem, we use the three following lemmas:
Lemma 2.2 The total amount of all cash is constant and equal to
the initial value, i.e., for each
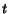
,
![\( \sum_{i=1}^{n} C_t[i]=\sum_{i=1}^{n}C_0[i]=1\)](./p7-abiteboul-img64.gif)
This is obvious by induction since we only distribute each node cash among
the children.
Lemma 2.3 After
each step
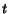
, we have for each page

,
The proof by induction is given in appendix. It works by considering two
cases: either  is read, or another page is read.
is read, or another page is read.
Lemma 2.4 If all pages
are infinitely read,
![$\sum_j{H_t[j]}$](./p7-abiteboul-img66.gif)
goes to infinity.
For this, we must prove that there is 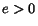 such
that starting at any time
such
that starting at any time 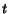 ,
,
![$\sum_j{H_t[j]}$](./p7-abiteboul-img66.gif) will eventually
increase of
will eventually
increase of 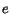 . Consider
. Consider 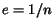 , i.e.
, i.e. 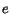 is the average value of cash on all
pages. At time
is the average value of cash on all
pages. At time 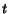 , there is a page
, there is a page  having more than
having more than 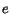 cash. The cash of page
cash. The cash of page  can not decrease until
can not decrease until  is read.
This page will be read one more time after
is read.
This page will be read one more time after 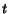 because
all pages are read infinitely often. Thus, the history of the page will
increase of at least
because
all pages are read infinitely often. Thus, the history of the page will
increase of at least 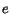 when page
when page  is read, and this will increase
is read, and this will increase
![$\sum_j{H_t[j]}$](./p7-abiteboul-img66.gif) . Now, we can prove, as
shown in appendix, that:
. Now, we can prove, as
shown in appendix, that:
Lemma 2.5
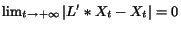
By Lemma 2.5, 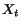 go infinitely close to a characteristic vector of
go infinitely close to a characteristic vector of 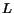 of the dominant characteristic value
of the dominant characteristic value 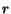 . This
suggests using
. This
suggests using 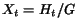 as an estimate of page
importance. We can add
as an estimate of page
importance. We can add 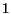 (i.e.
(i.e. ![$\sum_i C_t[i]$](./p7-abiteboul-img72.gif) ) to the denominator
) to the denominator 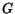 by using the cash accumulated since
last crawl, and thus have (on average) a marginally better estimate. More
precisely, one can use for page
by using the cash accumulated since
last crawl, and thus have (on average) a marginally better estimate. More
precisely, one can use for page  ,
,
The main advantage of our algorithm is that it allows focused crawling.
Because our algorithm is run online and its results are immediately available
to the crawler, we use it to focus crawling to the most interesting pages for
the users. This is in particular interesting in the context of building a web
archive [1], when there are
strong requirements (and constraints) on the crawling process. Moreover,
since we don't have to store the matrix but only a vector, our algorithm
presents the following advantages:
- It requires less storage resources than standard algorithms.
- It requires less CPU, memory and disk access than standard
algorithms.
- It is easy to implement.
Our algorithm is also well adapted to ``continuous'' crawl strategies. The
reason is that storing and maintaining the link matrix during a
``continuous'' crawl of the Web (when pages are refreshed often) is
significantly more expensive than for single ``snapshot'' crawl of the Web
(when each page is read only once). Indeed, when information about specific
pages has to be read and updated frequently, the number of random disk access
may become a limiting factor. In our experiment for instance, the crawler was
retrieving hundreds of pages per seconds on each PC (see Section 4). However, note that the storage
of a link matrix may be useful beyond the computation of page importance. For
instance, given a page 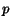 , Google provides the list of pages
pointing to it. This means that the matrix (or its transpose) is maintained
in some form. Another usage of the link matrix is exhibited in [14].
, Google provides the list of pages
pointing to it. This means that the matrix (or its transpose) is maintained
in some form. Another usage of the link matrix is exhibited in [14].
Crawling Strategies
In this section, we first consider different crawling strategies that impact
the convergence of our algorithm. Then, we study how they can be used in the
case of a changing graph. Implementations aspects and experiments are
considered in the next section.
As previously mentioned, the error in our estimate is bounded by
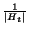 . Let us call
. Let us call
the error factor, although this is, strictly speaking, not the error
(but an upper bound for it). Now, in principle, one could choose a very bad
strategy that would very often select pages with very low cash. (The
correctness of the algorithm requires that each page is read infinitely many
times but does not require the page selection strategy to be smart.) On the
other hand, if we choose nodes with very large cash, the error factor
decreases faster. To illustrate, consider three page selection strategies:
- Random : We choose the next page to crawl randomly with equal
probability. (Fairness: for each
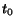 ,
the probability that a page will be read at some
,
the probability that a page will be read at some 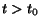 goes to 1 when
goes to 1 when 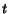 goes
to infinity.)
goes
to infinity.)
- Greedy : We read next the page with highest cash. This is a
greedy way to decrease the value of the error factor. (Fairness: For a
strongly connected graph, each page is read infinitely often because it
accumulates cash until it is eventually read. See Lemma 6.2 in appendix).
- Cycle : We choose some fixed order and use it to cycle around
the set of pages. (Fairness is obvious.) We considered this page
selection strategy simply to have a comparison with a systematic
strategy. Recall that systematic page selection strategies impose
undesired constraints on the crawling of pages.
Remark 3.1 (Xyleme ) The strategy for selecting the next page
to read used in Xyleme is close to
Greedy . It is tailored to
optimize our knowledge of the web [
20], the interest of clients for some
portions of the web, and the refreshing of the most important pages that
change often.
To get a feeling of how Random and Greedy progress, let us
consider some estimates of the values of the error factor for these two page
selection strategies. Suppose that at initialization, the total value of the
cash of all pages is 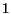 and that there are
and that there are 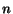 pages. Then:
pages. Then:
- Random : The next page to crawl is chosen randomly so its cash
is on average
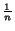 . Thus, the
denominator of the error factor is increased by
. Thus, the
denominator of the error factor is increased by 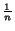 on average per page.
on average per page.
- Greedy : A page accumulates cash until it reaches the point
where it is read. Let
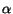 be the average
cash of a page at the time it is read. On average, the cash of the page
is
be the average
cash of a page at the time it is read. On average, the cash of the page
is 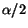 if we suppose that cash
is accumulated linearly by pages until they are read. This result has
been confirmed by experiments. Since the total of the cash is
if we suppose that cash
is accumulated linearly by pages until they are read. This result has
been confirmed by experiments. Since the total of the cash is 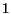 , this shows that
, this shows that 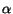 is
is 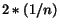 . Thus the denominator of the error factor is increased
by
. Thus the denominator of the error factor is increased
by 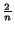 on average per page
read. This result has also been confirmed by experiments, the average
``cash'' value of crawled pages converges to
on average per page
read. This result has also been confirmed by experiments, the average
``cash'' value of crawled pages converges to 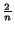 after crawling a few thousand pages.
after crawling a few thousand pages.
Thus the error factor decreases on average twice faster with Greedy
than with Random . We will see with experiments (in Section 4) that, indeed, Greedy
converges faster. Moreover, Greedy focuses our resources on the
important pages which corresponds to users interest. On these pages, the
error factor of greedy Greedy decreases even faster.
Consider now a dynamic graph (the case of the web). Pages come and disappear
and edges too. Because of the time it takes to crawl the Web (weeks or
months), our knowledge of the graph is not perfect. Page importance is now a
moving target and we only hope to stay close to it. It is convenient to think
of the variable  as the clock. Consider
two time instants
as the clock. Consider
two time instants 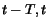 corresponding to
corresponding to 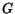 having the value
having the value 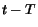 and
and 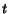 . Let
. Let ![$H_{t-T,t}[i]$](./p7-abiteboul-img86.gif) be the total of cash
added to the history of page
be the total of cash
added to the history of page  between time
between time 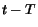 and
and 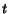 , i.e.,
, i.e.,
![$H_{t}[i]-H_{t-T}[i]$](./p7-abiteboul-img87.gif) . Let
. Let
Because the statement of Theorem 2.3 does not impose any condition
on the initial state of 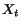 , it is obvious that
, it is obvious that 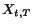 converges to the vector of importance when
converges to the vector of importance when 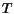 goes to infinity. (Note that on the other hand, for a fixed
goes to infinity. (Note that on the other hand, for a fixed 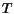 , when
, when 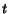 goes to infinity,
goes to infinity, 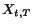 does not converge to the vector of importance.) Using the
data gathered between
does not converge to the vector of importance.) Using the
data gathered between 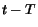 and
and 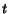 , comes to
ignoring the history before time
, comes to
ignoring the history before time 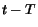 and starting with the
state of the cash at time
and starting with the
state of the cash at time 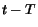 for initial state.
Observe that this state may be not more informative than the very first state
with equal distribution of cash. We thus estimate the importance of a page by
looking at the history between
for initial state.
Observe that this state may be not more informative than the very first state
with equal distribution of cash. We thus estimate the importance of a page by
looking at the history between 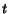 (now) and
(now) and 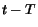 . We call the interval
. We call the interval ![$[t-T,t]$](./p7-abiteboul-img91.gif) the
(time) window. There is a trade-off between precision and
adaptability to changes and a critical parameter of the technique is the
choice of the size of the window.
We next describe (variants of) an algorithm, namely Adaptive OPIC, that
compute(s) page importance based on a time window. In Adaptive OPIC, we have
to keep some information about the history in a particular time window. We
considered the following window policies:
the
(time) window. There is a trade-off between precision and
adaptability to changes and a critical parameter of the technique is the
choice of the size of the window.
We next describe (variants of) an algorithm, namely Adaptive OPIC, that
compute(s) page importance based on a time window. In Adaptive OPIC, we have
to keep some information about the history in a particular time window. We
considered the following window policies:
- Fixed Window (of size
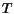 ): For every page
): For every page
 , we store the value of cash
, we store the value of cash ![$C_t[i]$](./p7-abiteboul-img92.gif) and the global value
and the global value 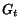 for all times it was crawled
since (now -
for all times it was crawled
since (now - 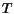 ).
).
- Variable Window (of size
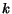 ): For every page
): For every page  , we store the value of cash
, we store the value of cash ![$C_t[i]$](./p7-abiteboul-img92.gif) and the global value
and the global value 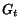 for the last
for the last 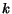 times this page was crawled.
times this page was crawled.
- Interpolation (of time
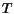 ): For every page
): For every page
 , we store only the
, we store only the 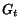 value when it was last
crawled, and an interpolated history
value when it was last
crawled, and an interpolated history ![$H[i]$](./p7-abiteboul-img94.gif) (to be defined) that estimates the cash it got in a time interval of size
(to be defined) that estimates the cash it got in a time interval of size
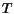 before that last crawl.
before that last crawl.
In the following, we call measure a pair (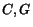 ). Note that in Variable Window, we store exactly
). Note that in Variable Window, we store exactly 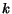 measures; and that in Interpolation, we store only one. Note
also that in Fixed Window, the number of measures varies from one page to
another. In our analysis of Adaptive OPIC, there will be two main dimensions:
(i) the page selection strategy that is used (e.g., Greedy or
Random ) and (ii) the window policy that is considered (e.g., Fixed
Window or Interpolation). Variable Window is the easiest to implement since
we have to maintain, for each page, a fixed number of values.
One must be aware that some pages will be read rarely (e.g., once in several
months), whereas others will be read perhaps daily. So there are huge
variations in the size of histories. For very large histories, it is
interesting to use compression techniques, e.g., to group several consecutive
measures into one. On the opposite, we have too few measures for very
unimportant pages. This has a negative impact on the speed of convergence of
the algorithm. By setting a minimum number of measures per page (say 3),
experiments show that we obtain better results. See Section 4.
It is tailored to use little resources. Indeed, for each page, the history
simply consists of two values. This is what we tested on real web data (See
Section 4). It is the policy
actually used in Xyleme [27,20,28]. It is based on a fixed time
window of size
measures; and that in Interpolation, we store only one. Note
also that in Fixed Window, the number of measures varies from one page to
another. In our analysis of Adaptive OPIC, there will be two main dimensions:
(i) the page selection strategy that is used (e.g., Greedy or
Random ) and (ii) the window policy that is considered (e.g., Fixed
Window or Interpolation). Variable Window is the easiest to implement since
we have to maintain, for each page, a fixed number of values.
One must be aware that some pages will be read rarely (e.g., once in several
months), whereas others will be read perhaps daily. So there are huge
variations in the size of histories. For very large histories, it is
interesting to use compression techniques, e.g., to group several consecutive
measures into one. On the opposite, we have too few measures for very
unimportant pages. This has a negative impact on the speed of convergence of
the algorithm. By setting a minimum number of measures per page (say 3),
experiments show that we obtain better results. See Section 4.
It is tailored to use little resources. Indeed, for each page, the history
simply consists of two values. This is what we tested on real web data (See
Section 4). It is the policy
actually used in Xyleme [27,20,28]. It is based on a fixed time
window of size 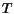 . The algorithm uses for history two
vectors
. The algorithm uses for history two
vectors
![$H[1..n],G[1..n]$](./p7-abiteboul-img96.gif) :
:
![$H[i]$](./p7-abiteboul-img94.gif) represents the sum of the
cash acquired by the page
represents the sum of the
cash acquired by the page  during a time period
during a time period
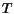 before the last crawl. This
value is obtained by interpolation.
before the last crawl. This
value is obtained by interpolation.![$G[i]$](./p7-abiteboul-img97.gif) is the
is the 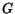 -time of that last crawl.
-time of that last crawl.
Figure 1: Simple
Interpolation
|
|
When we visit a page and update its history, we estimate the cash
that was added to that page in the interval 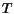 until
that visit. See Figure 1, for an
intuition of the interpolation. We know what was added to its cash between
time
until
that visit. See Figure 1, for an
intuition of the interpolation. We know what was added to its cash between
time ![$G[i]$](./p7-abiteboul-img97.gif) and
and 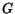 ,
, ![$C[i]$](./p7-abiteboul-img99.gif) . The interpolation assumes that the page accumulates cash
linearly. This has been confirmed by experiments. More precisely, the history
is updated as follows:
. The interpolation assumes that the page accumulates cash
linearly. This has been confirmed by experiments. More precisely, the history
is updated as follows:
When the number of nodes increases, the relative difficulty to assign a cash
and a history to new nodes highlights some almost philosophical issues about
the importance of pages. Consider the definition of importance based on  . When we crawl new pages, these pages acquire some
importance. The importance of previously known pages mechanically decreases
in average simply because we crawled more pages. This is true for instance in
the random walk model: adding new pages of non-null probability to be read
can only decrease the probability of other pages to be read. However, these
changes in pages importance seem unfair and are not expected by users of the
system. We assign to each new page a default history that corresponds to the
importance of recently introduced pages. Experiments confirmed this to be a
good estimate. The reason is that important pages are discovered first,
whereas new or recently introduced pages are often the least important ones.
In our system, the scheduling of pages to be read depends mostly on the
amount of ``cash'' for each page. The crawling speed gives the total number
of pages that we can read for both discovery and refresh. Our page importance
architecture allows us to allocate resources between discovery and refresh.
For instance, when we want to do more discovery, we proceed as follows: (i)
we take some cash from the virtual page and distribute it to pages that were
not read yet (ii) we increase the importance of ``small'' edges pointing to
the virtual page so that it accumulates more cash. To refresh more pages, we
do the opposite. We can also use a similar method to focus the crawl on a
subset of interesting pages on the web. For instance, we may use this
strategy to focus our crawling on XML pages [27,20]. In some other applications, we
may prefer to quickly detect new pages. For instance, we provide to a press
agency a 'copy tracker' that helps detecting copies of their News wires over
the web. The problem with News pages is that they often last only a few days.
In the OPIC algorithm, we process as follows for each link: pages that are
suspected to contain news wires (e.g. because the URL contains ``news'')
receive some ``extra'' cash. This cash is taken from the (unique) virtual
page so that the total value of cash in the system does not change. Other
criteria may be used, for instance we are working on the use of the links
semantic, e.g. by analyzing words found close to the HTML link anchor.
. When we crawl new pages, these pages acquire some
importance. The importance of previously known pages mechanically decreases
in average simply because we crawled more pages. This is true for instance in
the random walk model: adding new pages of non-null probability to be read
can only decrease the probability of other pages to be read. However, these
changes in pages importance seem unfair and are not expected by users of the
system. We assign to each new page a default history that corresponds to the
importance of recently introduced pages. Experiments confirmed this to be a
good estimate. The reason is that important pages are discovered first,
whereas new or recently introduced pages are often the least important ones.
In our system, the scheduling of pages to be read depends mostly on the
amount of ``cash'' for each page. The crawling speed gives the total number
of pages that we can read for both discovery and refresh. Our page importance
architecture allows us to allocate resources between discovery and refresh.
For instance, when we want to do more discovery, we proceed as follows: (i)
we take some cash from the virtual page and distribute it to pages that were
not read yet (ii) we increase the importance of ``small'' edges pointing to
the virtual page so that it accumulates more cash. To refresh more pages, we
do the opposite. We can also use a similar method to focus the crawl on a
subset of interesting pages on the web. For instance, we may use this
strategy to focus our crawling on XML pages [27,20]. In some other applications, we
may prefer to quickly detect new pages. For instance, we provide to a press
agency a 'copy tracker' that helps detecting copies of their News wires over
the web. The problem with News pages is that they often last only a few days.
In the OPIC algorithm, we process as follows for each link: pages that are
suspected to contain news wires (e.g. because the URL contains ``news'')
receive some ``extra'' cash. This cash is taken from the (unique) virtual
page so that the total value of cash in the system does not change. Other
criteria may be used, for instance we are working on the use of the links
semantic, e.g. by analyzing words found close to the HTML link anchor.
Implementation and experiments
We implemented and tested first the standard off-line algorithm for computing
page importance, then variants of Adaptive OPIC. We briefly describe some
aspects of the implementation. We then report on experiments first on
synthetic data, then on a large collection of web pages.
Our implementation of the off-line algorithm is standard and will not be
discussed here. We implemented a distributed version of Adaptive OPIC that
can be parameterized to choose a page selection strategy, a window policy, a
window size, etc. Adaptive OPIC runs on a cluster of Linux PCs. The code is
in C++. Corba is used for communications between the PCs. Each crawler is in
charge of a portion of the pages of the web. The choice of the next page to
read by a crawler is performed by a separate module (the Page Scheduler). The
split of pages between the various crawlers is made using a hash function
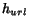 of the URLs. Each crawler
evaluates the importance of pages it is in charge of. Its portion of the cash
vector is in main memory, whereas its portion of the history is on disk. The
crawler also uses an (in memory) hash table that allows to map a URL handled
by this crawler to its identifier (an integer) in the system. Finally, it
uses a map from identifiers to URLs. This last map may reside on disk. Each
crawler crawls millions of pages per day. The bandwidth was clearly the
limiting factor in the experiments. For each page that is crawled, the
crawler receives the identifier of a page from the page scheduler and then
does the following:
of the URLs. Each crawler
evaluates the importance of pages it is in charge of. Its portion of the cash
vector is in main memory, whereas its portion of the history is on disk. The
crawler also uses an (in memory) hash table that allows to map a URL handled
by this crawler to its identifier (an integer) in the system. Finally, it
uses a map from identifiers to URLs. This last map may reside on disk. Each
crawler crawls millions of pages per day. The bandwidth was clearly the
limiting factor in the experiments. For each page that is crawled, the
crawler receives the identifier of a page from the page scheduler and then
does the following:
- Fetch: It obtains the URL of the page, fetches the page from
the web and parses it;
- Money transfers: It distributes the current cash of the page
to the pages it points to. For each such page, it uses
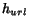 to obtain the name of the server in charge of that
page. It sends a ``money transfer'' to that server indicating the URL
of the page and the amount. This is a buffered network call.
to obtain the name of the server in charge of that
page. It sends a ``money transfer'' to that server indicating the URL
of the page and the amount. This is a buffered network call.
- Records: It updates the history of the page and resets its
cash to null. Updating the history requires one disk access.
Each crawler also processes the money transfer orders coming from other
servers. Communications are asynchronous. It should be observed that for each
page crawled, there are only two disk accesses, one to obtain the metadata of
the page and one to update the metadata, including the history. Besides that,
there are Corba communications (on the local network), and main memory
accesses.
Although we started our experiments with large collection of URLs on the web,
synthetic data gave us more flexibility to study various input and output
parameters, such as: graph size, graph connectivity, change rates, types of
changes, distribution of in-degrees, out-degrees and page importance,
importance error, ranking errors.
We performed experiments with various synthetic graphs containing dozens of
millions of web pages. These experiments showed that the use of very large
graphs did not substantially alter the results. For instance, we started with
graphs obtained using a Poisson distribution on the average of incoming
links, a somewhat simplistic assumption. We then performed experiments with
more complex distributions following recent studies of the web graph [4], e.g., with a power
distribution
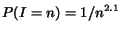 . Results were
rather similar to those obtained using a Poisson distribution. In order to
also control the distribution of outgoing links and the correlations between
them, we tried several graph models in the spirit of [8], but even with significant
changes of the graph parameters, the patterns of the results did not change
substantially from the simple graph model. So, we then restricted our
attention to rather simple graphs of reasonably small size to be able to test
extensively, e.g., various page selection strategies, various window sizes,
various patterns of changes of the web. In the remaining of this section, we
will consider a simple graph model based on the power distribution on
incoming edges. Details omitted. The number of nodes is fixed to N =
100 000 nodes.
First, we studied the convergence of OPIC for various page selection
strategies. We considered Random , Cycle and
Greedy . We compared the values of the estimates at different points
in the crawl, after crawling
. Results were
rather similar to those obtained using a Poisson distribution. In order to
also control the distribution of outgoing links and the correlations between
them, we tried several graph models in the spirit of [8], but even with significant
changes of the graph parameters, the patterns of the results did not change
substantially from the simple graph model. So, we then restricted our
attention to rather simple graphs of reasonably small size to be able to test
extensively, e.g., various page selection strategies, various window sizes,
various patterns of changes of the web. In the remaining of this section, we
will consider a simple graph model based on the power distribution on
incoming edges. Details omitted. The number of nodes is fixed to N =
100 000 nodes.
First, we studied the convergence of OPIC for various page selection
strategies. We considered Random , Cycle and
Greedy . We compared the values of the estimates at different points
in the crawl, after crawling 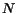 pages, up to to
pages, up to to 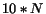 pages. The error we compute is
the mean over the set of pages of the error between the computation of OPIC
at this state and the value of the fixpoint. More precisely, we compute the
average of the percentage of error:
pages. The error we compute is
the mean over the set of pages of the error between the computation of OPIC
at this state and the value of the fixpoint. More precisely, we compute the
average of the percentage of error:
where 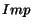 is obtained by running the
off-line algorithm until a fixpoint is reached (with negligible error).
is obtained by running the
off-line algorithm until a fixpoint is reached (with negligible error).
Figure 2: Convergence of OPIC (on
all pages)
|
|
Consider Figure 2. The error
is about the same for Greedy and Cycle . This result was
expected since previous studies [13] show that given a
standard cost model, uniform refresh strategies perform as good as focused
refresh. As we also expected, Random performs significantly worse.
We also compared these, somewhat artificially, to the off-line algorithm. In
the off-line, each iteration of the matrix is a computation on 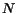 pages, so we count
pages, so we count 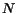 ``crawled pages'' for each iteration. The off-line algorithm converges
almost like Cycle and Greedy . This is not surprising since
the crawl of
``crawled pages'' for each iteration. The off-line algorithm converges
almost like Cycle and Greedy . This is not surprising since
the crawl of 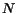 pages with Cycle
corresponds roughly to a biased iteration on the matrix.
pages with Cycle
corresponds roughly to a biased iteration on the matrix.
Figure 3: Convergence of OPIC (on
important pages)
|
|
Now consider Figure 3. The error
is measured now only for the top ten percent pages, the interesting ones in
practice. For this set of pages, Greedy (that is tailored to
important pages) converges faster than the others including the off-line
algorithm. We also studied the variance. It is roughly the same for all page
selection strategies, e.g., almost no page had a relative error more than
twice the mean error. We also considered alternative error measures. For
instance, we considered an error weighted with page importance or the error
on the relative importance that has been briefly mentioned. We also
considered the error in ordering pages when their importance is used to rank
query results. All these various error measures lead to no significant
difference in the results.
Figure 4: Influence of window's
sizes
|
|
As already mentioned, a small window means more reactivity to changes but at
the cost of some lack of precision. A series of experiments was conducted to
determine how much. To analyze the impact of the size of the window, we use
Adaptive OPIC with the Greedy strategy and a Fixed Window of 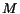 crawls, i.e., we keep for each
page the history since the last
crawls, i.e., we keep for each
page the history since the last 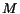 crawls of the page.
Similar results were obtained with other variants of the algorithm. Consider
Figure 4 ignoring the
Interpolation policy for the moment. The change rate is the number of pages
that have their in-degree significantly modified (i.e. divided par two or
multiplied by two) during the time of crawling
crawls of the page.
Similar results were obtained with other variants of the algorithm. Consider
Figure 4 ignoring the
Interpolation policy for the moment. The change rate is the number of pages
that have their in-degree significantly modified (i.e. divided par two or
multiplied by two) during the time of crawling 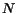 pages,
where
pages,
where 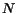 is the number of pages on the
graph (i.e. the time for ``one'' crawl of the graph). For each change rate
the graph is crawled ten times. The figure shows the result for
is the number of pages on the
graph (i.e. the time for ``one'' crawl of the graph). For each change rate
the graph is crawled ten times. The figure shows the result for 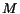 = 4, 8, 16. The important point to
notice is that we can get reasonably close to the fixpoint with rather small
windows (e.g.,
= 4, 8, 16. The important point to
notice is that we can get reasonably close to the fixpoint with rather small
windows (e.g., 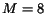 here). As previously mentioned,
the trade-off is reactivity to changes versus precision. When the time window
becomes too small (e.g.,
here). As previously mentioned,
the trade-off is reactivity to changes versus precision. When the time window
becomes too small (e.g., 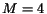 here), the error is
more important. This is because each measure for a page gives only a too
rough estimate of this page importance, so the error is too large. Such an
error may still be acceptable for some applications. Now observe the
Interpolation experiment in Figure 4. First, note that it performs
almost as well as large Variable Window (e.g.
here), the error is
more important. This is because each measure for a page gives only a too
rough estimate of this page importance, so the error is too large. Such an
error may still be acceptable for some applications. Now observe the
Interpolation experiment in Figure 4. First, note that it performs
almost as well as large Variable Window (e.g. 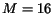 ) on
graph with few changes. Also, it adapts better to higher change rates (e.g.
more than 1 percent). So, let us consider now the comparison of various
window policies.
We compared different policies for keeping the history. In this report, we
use again the Greedy strategy. Various window policies may require
different resources. To be fair, we chose policies that roughly requested
similar amount of resources. Typically, we count for storage the number of
measures we store. (Recall that a measure consists of a value for
) on
graph with few changes. Also, it adapts better to higher change rates (e.g.
more than 1 percent). So, let us consider now the comparison of various
window policies.
We compared different policies for keeping the history. In this report, we
use again the Greedy strategy. Various window policies may require
different resources. To be fair, we chose policies that roughly requested
similar amount of resources. Typically, we count for storage the number of
measures we store. (Recall that a measure consists of a value for 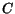 and one for
and one for 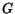 .) The five policies we
compared used between 4 and 8 measures, except Interpolation that by
definition uses only 1. Figure 5
shows the average number of measures used per page in each case. These
measures depend for Fixed Window on the crawling speed which was set here to
be
.) The five policies we
compared used between 4 and 8 measures, except Interpolation that by
definition uses only 1. Figure 5
shows the average number of measures used per page in each case. These
measures depend for Fixed Window on the crawling speed which was set here to
be 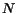 pages per month (the speed was
chosen here so that Fixed Window would use about as much resources as the
others). We also considered a variant of Fixed Window that forces each page
to have a minimum number of measures, namely Improved Fixed Window. We
required for the experiment mentioned here a minimum of 3 measures. Note that
this resulted for this particular data set in an increase of the average
number of measures from
pages per month (the speed was
chosen here so that Fixed Window would use about as much resources as the
others). We also considered a variant of Fixed Window that forces each page
to have a minimum number of measures, namely Improved Fixed Window. We
required for the experiment mentioned here a minimum of 3 measures. Note that
this resulted for this particular data set in an increase of the average
number of measures from 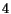 to
to 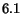 .
.
Figure 5: Storage resources per
time window
| Window Type and Size |
Measures per page |
| Variable Window 8 measures |
8 |
| Fixed Window 8 months |
8.4 |
| Improved Fixed Window 4 months |
6.1 |
| Interpolation 4 months |
1 |
|
Figure 6: Influence of window's
types
|
|
Now consider Figure 6. It
shows that for a similar number of measures, Variable Window performs better
than Fixed Window. The problem with Fixed Window is that very few measures
are stored for unimportant pages and the convergence is very slow because of
errors on such pages. On the other hand, the Improved Fixed Window policy
yields significantly better results. The improvement comes indeed from more
reliability for unimportant pages. The most noticeable result about the use
of windows is that the algorithm with the Interpolation policy outperforms
the other variants while consuming less resources. Indeed, the error
introduced by the interpolation is negligible. Furthermore, the interpolation
seems to avoid some ``noise'' introduced when an old measure is added (or
removed) in Adaptive OPIC. In some sense, the interpolation acts as a filter
on the sequence of measures. Of course the convergence of all variants of the
adaptive algorithms depends on the time window that is used. The excellent
behavior of Interpolation convinced us to adopt it for our experiments with
crawls of the web. This is considered next.
Web data
We performed the web experiments using the crawlers of Xyleme [28]. The crawl used the page
selection strategy of Xyleme that has been previously mentioned and is
related to Greedy . The history was managed using the Interpolation
policy. During the test, the number of PCs varied from 2 to 8. Each PC had
little disk space and less than 1.5Gb of main memory. Some reasonable
estimate of page importance for the most important pages was obtained in a
few days, as important pages are read more frequently and discovered sooner
than others. The experiments lasted for several months. We discovered one
billion URLs; only 400 millions of them were actually read. Note that because
of the way we discover pages, these are 400 million relatively important
pages. Moreover, we could give reasonable importance estimates even on pages
that were never read. This experiment was sufficient (with limited human
checking of the results) to conclude that the algorithm could be used in a
production environment. Typically, for all practical uses of importance we
considered (such as ranking query results or scheduling page refresh), the
precision brought by the algorithm is rapidly sufficient. An advantage of the
algorithm is also that it rapidly detects the new important pages, so they
can be read sooner. A main issue was the selection of the size of the time
window. We first fixed it too small which resulted in undesired variations in
the importance of some pages. We then used a too large window and the
reactivity to changes was too limited. Finally, the window was set to 3
months. This value depends on the crawling speed, which in our case was
limited by the network bandwidth. Our performance analysis also showed that
using our system (Xyleme crawler and Adaptive OPIC), it is possible to, for
instance, crawl and compute page importance (as well as maintain this
knowledge) for a graph of up to 2 billions pages with only 4 PCs equipped
each with 4Gb of main memory and a small disk. In the context of Web
Archiving [1], we also conducted
experiments to decide if our measures of page importance could be used to
select pages of interest for the French national Library. We selected
thousand web sites, and 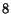 different professional librarians
ranked each site in order to decide which sites should be archived (on a 1 to
4 scale). We defined the reference value for each site based on the average
of these rankings. Finally, we defined the 'score' of a librarian as the
number of sites in which his rank was identical to the reference. The scores
of librarians ranged from 60 to 80 percent, and the score of our page
importance measures was 65 percent. This means that our measure based only on
page importance was as good as a professional librarian, although not as good
as the best ones. We are currently working on using other criteria [1] to improve the ``automatic''
librarian.
different professional librarians
ranked each site in order to decide which sites should be archived (on a 1 to
4 scale). We defined the reference value for each site based on the average
of these rankings. Finally, we defined the 'score' of a librarian as the
number of sites in which his rank was identical to the reference. The scores
of librarians ranged from 60 to 80 percent, and the score of our page
importance measures was 65 percent. This means that our measure based only on
page importance was as good as a professional librarian, although not as good
as the best ones. We are currently working on using other criteria [1] to improve the ``automatic''
librarian.
During our experiments, we found out that the semantics of links in dynamic
pages is (often) not as good as in pages fully written by authors. Links
written by authors usually points to more relevant pages. On the other hand,
most links in dynamic pages often consist in other (similar) queries to the
same database. For instance, forum archives or catalog pages often contain
many links that are used to browse through classification. Similarly, we
found out that ``internal'' links (links that point to a page on the same web
site) are less useful to discover other relevant pages than ``external''
links (links to a page on some other web site). To solve both problems, we
are currently working on a notion of site-based importance [1] that consider links between web-sites
instead of links between web-pages. We are currently experimenting our
algorithm with this new notion of importance per site.
We proposed a simple algorithm to implement with limited resources a
realistic computation of page importance over a graph as large as the web. We
demonstrated both the correctness and usability of the technique. Our
algorithm can be used to improve the efficiency of crawling systems since it
allows to focus on-line the resources to important pages. It can also be
biased to take into account specific fields of interest for the
users [1]. More experiments on
real data are clearly needed. It would be in particular interesting to test
the variants of Adaptive OPIC with web data. However, such tests are quite
expensive. To understand more deeply the algorithms, more experiments are
being conducted with synthetic data. We are experimenting with various
variants of Adaptive OPIC. We believe that better importance estimates can be
obtained and are working on that. One issue is the tuning of the algorithms
and in particular, the choice of (adaptable) time windows. We are also
continuing our experiments on changing graphs and in particular on the
estimate of the derivative of the importance. We finally want to analyze more
in-depth the impact of various specific graph patterns as done in [17] for the off-line algorithm.
We are also working on a precise mathematical analysis of the convergence
speed of the various algorithms. The hope is that this analysis will provide
us with bounds of the error of the importance, and will also guide us in
fixing the size of windows and evaluating the changes in importance. We are
also improving the management of newly discovered pages. The algorithm
presented here computes page importance that depends on the entire graph by
looking at one page at a time independently of the order of visiting the
pages. It would be interesting to find other properties of graph nodes that
can be computed similarly.
We want to thank Luc Segoufin, Laurent Mignet and Tova Milo for discussions
on the present work.
-
- 1
- S. Abiteboul, G. Cobena, J. Masanes, and
G. Sedrati.
A first experience in archiving the french web.
ECDL, 2002.
- 2
- S. Abiteboul, M. Preda, and G. Cobena.
Computing web page importance without storing the graph of the web
(extended abstract).
IEEE-CS Data Engineering Bulletin, Volume 25, 2002.
- 3
- Alta vista.
http://www.altavista.com/.
- 4
- Andrei Z. Broder and al.
Graph structure in the web.
WWW9/Computer Networks, 2000.
- 5
- Steve Chien, Cynthia Dwork, Ravi Kumar, Dan Simon, and
D. Sivakumar.
Link evolution: Analysis and algorithms.
In Workshop on Algorithms and Models for the Web Graph (WAW),
2002.
- 6
- Junghoo Cho, Hector García-Molina, and Lawrence Page.
Efficient crawling through URL ordering.
Computer Networks and ISDN Systems, 30(1-7):161-172, 1998.
- 7
- Kai Lai Chung.
Markov chains with stationary transition probabilities.
Springer, 1967.
- 8
- Colin Cooper and Alan M. Frieze.
A general model of undirected web graphs.
In European Symposium on Algorithms, pages 500-511, 2001.
- 9
- Y. Dong D. Zhang.
An efficient algorithm to rank web resources.
9 th International World Wide Web Conference, 2000.
- 10
- F. R. Gantmacher.
Applications of the theory of matrices.
In Interscience Publishers, pages 64-79, 1959.
- 11
- Google.
http://www.google.com/.
- 12
- T. Haveliwala.
Efficient computation of pagerank.
Technical report, Stanford University, 1999.
- 13
- H. Garcia-Molina J. Cho.
Synchronizing a database to improve freshness.
SIGMOD, 2000.
- 14
- M.R. Henzinger J. Dean.
Finding related pages in the world wide web.
8th International World Wide Web Conference, 1999.
- 15
- A. Broder K. Bharat.
Estimating the relative size and overlap of public web search engines.
7th International World Wide Web Conference (WWW7), 1998.
- 16
- Jon M. Kleinberg.
Authoritative sources in a hyperlinked environment.
Journal of the ACM, 46(5):604-632, 1999.
- 17
- G.V. Meghabghab.
Google's web page ranking applied to different topological web graph
structures.
JASIS 52(9), 2001.
- 18
- Rajeev Motwani and Prabhakar Raghavan.
Randomized algorithms.
ACM Computing Surveys, 28(1):33-37, 1996.
- Lawrence Page, Sergey Brin, Rajeev Motwani, and Terry Winograd.
The pagerank citation ranking: Bringing order to the web, 1998.
- 20
- M. Preda.
Data acquisition for an xml warehouse.
DEA thesis Paris 7 University, 2000.
- 21
- L. Page S. Brin.
The anatomy of a large-scale hypertextual web search engine.
WWW7 Conference, Computer Networks 30(1-7), 1998.
- 22
- B. Dom S. Chakrabarti, M. van den Berg.
Focused crawling: a new approach to topic-specific web resource
discovery.
8th World Wide Web Conference, 1999.
- 23
- L. Giles S. Lawrence.
Accessibility and distribution of information on the web.
Nature, 1999.
- 24
- Search-engine watch.
www.searchenginewatch.com/.
- 25
- S. Toledo.
Improving the memory-system performance of sparse-matrix vector
multiplication.
IBM Journal of Research and Development, 41(6):711-??, 1997.
- 26
- C.J. van Rijsbergen.
Information retrieval.
London, Butterworths, 1979.
- 27
- Lucie Xyleme.
A dynamic warehouse for xml data of the web.
IEEE Data Engineering Bulletin, 2001.
- 28
- Xyleme.
www.xyleme.com.
Lemma 5.1 (see lemma
2.3) After each step
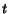
, we have for each page

,
The proof is by induction. Clearly, the lemma is true at time 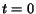 . Suppose it is true at time
. Suppose it is true at time 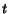 for each
element
for each
element  . Consider element
. Consider element  at step
at step 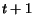 . At step
. At step 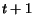 a page
a page 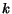 is crawled. Two cases may occur: If
is crawled. Two cases may occur: If
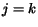 , then the right term doesn't
change:
, then the right term doesn't
change:
![$\forall i, i\neq j, H_{t+1}[i]=H_t[i]$](./p7-abiteboul-img122.gif) . The left term value doesn't change either, the cash is added to
. The left term value doesn't change either, the cash is added to  and then set to zero. So
and then set to zero. So
![$H_{t+1}[j]+C_{t+1}[j]=H_t[j]+C_t[j]$](./p7-abiteboul-img123.gif) ,
and the equation is true at
,
and the equation is true at 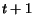 . If
. If 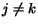 . Then
. Then ![$C_{t+1}[j]$](./p7-abiteboul-img125.gif) increases by
increases by
![$C_t[k]*\frac{L[i,j]}{out[i]}$](./p7-abiteboul-img126.gif) . So
. So
Now
![\(\forall i, i\neq k, H_{t+1}[i]=H_t[i]\)](./p7-abiteboul-img129.gif) , and also
, and also
![\(H_{t+1}[k]=H_t[k]+C_t[k]\)](./p7-abiteboul-img130.gif) , and this
shows the result.
, and this
shows the result.
Lemma 5.2 Consider a
strongly connected graph.
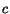
in the cash of any node

eventually leads to
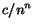
in the cash of

. For each

,
![$H_t[j]$](./p7-abiteboul-img133.gif)
goes to infinity.
Each node splits the value by at most 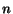 , because
it can't have more than
, because
it can't have more than 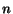 different links. We suppose that the
graph is strongly connected, so there is a path from
different links. We suppose that the
graph is strongly connected, so there is a path from  to
to  , and it is no longer than
, and it is no longer than 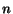 . Let's note
. Let's note 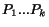 the pages for
this path. We suppose that every page is crawled an infinite number of times.
So we eventually will crawl
the pages for
this path. We suppose that every page is crawled an infinite number of times.
So we eventually will crawl 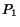 , then eventually
, then eventually 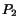 , ... until
, ... until 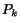 . Thus we will eventually have distributed at least
. Thus we will eventually have distributed at least 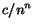 in the cash of
in the cash of  . Consider any moment
. Consider any moment 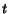 , some node contains at least
, some node contains at least 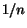 cash (because
cash (because
![$\sum_{i}C_t[i]=1$](./p7-abiteboul-img138.gif) ). Thus, it will
eventually increase the cash of
). Thus, it will
eventually increase the cash of  (thus eventually its
history) by
(thus eventually its
history) by 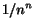 . Thus
. Thus ![$H_t[j]$](./p7-abiteboul-img133.gif) goes to infinity.
goes to infinity.
Lemma 5.3
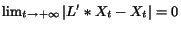
By definition of 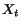 , for each
, for each  ,
,
Then, by Lemma 2.3,
Let us look at the  th coordinate of
th coordinate of 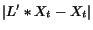 :
:
Its limit is 0 because, when 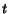 goes to infinity,
goes to infinity,
![$\sum_j{H_t[j]}$](./p7-abiteboul-img66.gif) goes to infinity (by
lemma 2.4) and
goes to infinity (by
lemma 2.4) and ![$C_0[j]$](./p7-abiteboul-img143.gif) ,
, ![$C_t[j]$](./p7-abiteboul-img144.gif) are
bounded by 1.
are
bounded by 1.
Theorem 5.4 The limit of
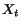
is
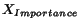
, i.e.,
By the previous result,
where 1 is the identity matrix (1 in the diagonal and 0 elsewhere). Consider
now the decomposition of 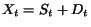 where
where 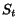 is in
is in 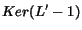 (the kernel of matrix
(the kernel of matrix 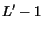 ), and
), and
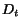 in the corresponding orthogonal
space where the restriction of
in the corresponding orthogonal
space where the restriction of 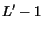 is invertible.
Because
is invertible.
Because 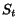 is in
is in 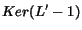 , we have
, we have
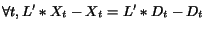 and so
and so
We can now restrict to the orthogonal space of 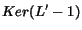 , in which
, in which 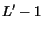 has an inverse called
has an inverse called  . The matrix multiplication being continuous, we can multiply to
the left by
. The matrix multiplication being continuous, we can multiply to
the left by  , which is constant, and thus
, which is constant, and thus
Now if we use the fact that there is a single fixpoint solution for 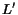 , that mean that
, that mean that 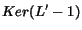 is of
dimension
is of
dimension  and that
and that
where 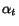 is a scalar. Now because
is a scalar. Now because
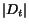 converges to zero,
and
converges to zero,
and
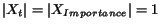 , we have:
, we have:
Footnotes
![[*]](./p7-abiteboul-footnote.gif)
- Google [11] seems to use such
a strategy for refreshing pages; Xyleme [28] does.
![[*]](./p7-abiteboul-footnote.gif)
- Note that the converse is true in the sense that if the graph is not
aperiodic it is always possible to find an
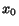 such that
such that 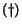 does not converge
does not converge
![[*]](./p7-abiteboul-footnote.gif)
- Greater values of
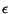 increase
the convergence speed
increase
the convergence speed
Gregory Cobena, 2003-02-25, INRIA (Domaine de Voluceau, Rocquencourt BP105, 78153 Le Chesnay), France

![[*]](./p7-abiteboul-footnote.gif) and when
crawling for new pages, important pages have to be fetched first [6]. Following some ideas of [16], Page and Brin
proposed a notion of page importance based on the link structure of the web
[21]. This was then used by
Google with a remarkable success. Intuitively, a page is important if there
are many important pages pointing to it. This leads to a fixpoint computation
by repeatedly multiplying the matrix of links between pages with the vector
of the current estimate of page importance until the estimate is stable,
i.e., until a fixpoint is reached.
and when
crawling for new pages, important pages have to be fetched first [6]. Following some ideas of [16], Page and Brin
proposed a notion of page importance based on the link structure of the web
[21]. This was then used by
Google with a remarkable success. Intuitively, a page is important if there
are many important pages pointing to it. This leads to a fixpoint computation
by repeatedly multiplying the matrix of links between pages with the vector
of the current estimate of page importance until the estimate is stable,
i.e., until a fixpoint is reached.![[*]](./p7-abiteboul-footnote.gif) .
.
![\begin{displaymath} \begin{array}{lll} H[i]*\frac{T - (G - G[i])}{T} + C[i] &&... ... C[i]*\frac{T}{G - G[i]} && \makebox{otherwise} \end{array} \end{displaymath}](./p7-abiteboul-img100.gif)
![\begin{displaymath} C_0[j] + \sum_{(i~ancestor~of~j)} ( \frac{L[i,j]}{out[i]} *H_t[i] ) +C_t[k]*\frac{L[k,j]}{out[k]} \end{displaymath}](./p7-abiteboul-img128.gif)
![\begin{displaymath}H_t[j]+C_t[j] = C_0[j] + \sum_{(i~ancestor~of~j)} ( \frac{L[i,j]}{out[i]} *H_t[i] ) \end{displaymath}](./p7-abiteboul-img65.gif)
![[*]](./p7-abiteboul-footnote.gif)
![[*]](./p7-abiteboul-footnote.gif)
![[*]](./p7-abiteboul-footnote.gif)