

Next:Combining
the HITS-based AlgorithmsUp:Improvement
of HITS-based AlgorithmsPrevious:Current
HITS-based Algorithms and
A New Weighted HITS-based Algorithm
Without content analysis, both BHITS and HITS can not solve the above problem.
BHITS only gives the links on the same host/document small weights, whose
sum equals to 1. While in the above problem, most of the out-links of a
small-in-large-out
link are in different domains. HITS usually makes the problem worse because
it gives the same weight to all the documents in the base set. In this
section, without resorting to content analysis, user feedback, or Web log
records, to prevent the BHITS algorithm and HITS algorithm from converging
to such small-in-large-out links, we use the link information in
the base set, and add more weights to the in-links of root set links if
a small-in-large-out link exists. In the new method, the equations
(1) and (2)
are modified as follows:
-
For all
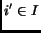 which points to
which points to 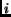 ,
,
 |
(3) |
-
For all
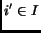 which is pointed to by
which is pointed to by 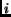 ,
,
 |
(4) |
In equation (3), the value of 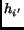 can be HITS hub weight, BHITS hub weight, or the hub weight of other HITS-based
algorithms. Similarly, this applies to the value of
can be HITS hub weight, BHITS hub weight, or the hub weight of other HITS-based
algorithms. Similarly, this applies to the value of 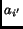 in equation (4).
in equation (4).
In our current implementation, all the 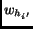 values are set to 1. The setting of
values are set to 1. The setting of 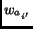 consists of two parts:
consists of two parts:
-
Before starting a HITS-based algorithm, if there exists a root link whose
in-degree is among the three smallest ones and whose out-degree is among
the three largest ones, then set
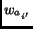 to 4 for in-links of all the root links.
to 4 for in-links of all the root links.
-
Otherwise, set all
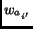 to 1. Run the HITS-based algorithm for one iteration without normalization.
If there exists a root link whose authority value is among the three smallest
ones and whose hub value is among the three largest ones, set
to 1. Run the HITS-based algorithm for one iteration without normalization.
If there exists a root link whose authority value is among the three smallest
ones and whose hub value is among the three largest ones, set 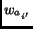 to 4 for in-links of all the root links.
to 4 for in-links of all the root links.
In the above two steps, usually the in-degree of a small-in-large-out
link is as small as 0, 1, or 2, while the out-degree can be more than several
hundred. Intuitively, in most cases, it is hard to believe that a root
link with no or few in-links can point to many highly relevant documents.
Even if it points to many good documents, due to the large number of documents
in the base set, there may be some duplicates between the out-links of
the small-in-large-out link and the neighborhood of other links,
and these good duplicated documents still have the chance to top the hub
set or the authority set. The method of setting in-link weights are very
simple and can be further improved by adaptively changing the weights of
both in- and out-links of a small-in-large-out link.
Let's use WBHITS to represent the weighted BHITS algorithm. The bottom
half of Table 1 shows the top 10
authorities and top 10 hits from WBHITS, which are much better than those
from BHITS.


Next:Combining
the HITS-based AlgorithmsUp:Improvement
of HITS-based AlgorithmsPrevious:Current
HITS-based Algorithms and
2002-02-18
![]() values are set to 1. The setting of
values are set to 1. The setting of ![]() consists of two parts:
consists of two parts: