Copyright is held by the author/owner(s).
WWW2002, May 7-11, 2002, Honolulu, Hawaii, USA.
ACM 1-58113-449-5/02/0005.
It is difficult to serialize an RDF graph as a humanly readable RDF/XML document. This paper describes the approach taken in Jena 1.2, in which a design pattern of guarded procedures invoked using top-down recursive descent is used. Each procedure corresponds to a grammar rule; the guard makes the choice about the applicability of the production. This approach is seen to correspond closely to the design of an LL(k) parser, and a theoretical justification of this correspondence is found in universal algebra.
D.3.4 [Programming Languages]: Processors - code generation, parsing
Algorithms, Design, Languages.
Parsing, unparsing, generation, grammar, universal algebra, XML, RDF.
This paper discusses the high level design of the output routines for the RDF/XML abbreviated syntax [19] within the Jena toolkit [20]. We propose a new design pattern for top down recursive descent unparsers which generate output according to a grammar.
Output is usually regarded in computer science as unproblematic. There is much more work on input than output. The work on input concentrates on formally structured input: parsing.
RDF/XML output is considerably more difficult than XML output because of the range of choices that must be made. There are very many different serializations of the same abstract RDF graph, most of these being decidedly nonoptimal for the human reader.
RDF/XML abbreviated syntax is too difficult for a straightforward approach to output that does not make explicit reference in its design to the RDF grammar.
We will show how the design pattern of top down recursive descent parsers [1] can be reused for 'unparsing' i.e. (top down recursive descent) generation using the grammar. This is placed in the context of Rus's algebraic formulation of the languages problem [25], which reveals the natural symmetry between parsing and unparsing.
We discuss the detailed considerations on which the runtime choices in an RDF/XML unparser are made.
The first use of most acronyms is followed by the standard reference, whose title expands the acronym, e.g. XML [6].
The word 'graph' is used to refer to the RDF abstract syntax, whereas the word 'tree' is used to refer to derivation trees from a grammar.
The main body of the paper refers to implemented work. Parts that are not implemented are so indicated by footnotes.
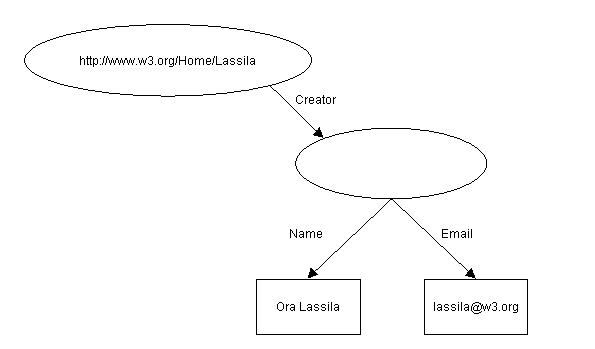
The drawings are taken from RDF Model and Syntax [19] and follow the conventions there that ovals are used for blank nodes and nodes labelled with URI references, whereas rectangles are used for nodes labelled with strings.
Following the RDF Model Theory [15], we see that an RDF document is a serialization of a graph. The graph is directed, with edges labelled with URIs [4], and some nodes also labelled with URIs. No URI labels two nodes. The unlabelled nodes are called 'blank nodes'. (Note: this graph is referred to as the model by the older Model & Syntax [19] specification, we avoid this confusing terminology in this paper).
When building output routines for RDF/XML the first task is to tackle the basic syntax (see M&S [19]). This is reassuringly boring: RDF/XML syntax appears to be no more sophisticated than a print statement wrapped in a couple of loops. However, the output, despite being XML, is only machine-readable. People cannot understand it. A DAML ontology [16] read in and written out by an RDF processor becomes unintelligible to the DAML expert. A CC/PP profile [18] is mangled to the point of ceasing to be a CC/PP profile. RDF/XML is only human readable in its abbreviated form.
A worry when writing a basic syntax output routine is what to do about the blank nodes1. The basic syntax requires the use of a URI to label the node. The usual solution is to use a gensym. However, this is unsatisfactory since the labeling of the node changes the meaning of the document with respect to the model theory or simply to graph equality [8].
The abbreviated form (see M&S [19] and the rearticulation2 [2]) is (intended to be) logically equivalent to the basic syntax. However it allows a number of new constructions which provide alternative ways of saying the same thing. Typically these new ways are more compact.
For example, the graph in Figure 1,
is serialized in the basic syntax as:
<rdf:RDF
xmlns:rdf=
"http://www.w3.org/1999/02/22-rdf-syntax-ns#"
xmlns:s=
"http://description.org/schema/">
<rdf:Description rdf:about=
"http://www.w3.org/Home/Lassila">
<s:Creator rdf:resource=
"http://gensym.org/blankNode1"/>
</rdf:Description>
<rdf:Description rdf:about=
"http://gensym.org/blankNode1">
<s:Name>Ora Lassila</s:Name>
<s:Email>lassila@w3.org</s:Email>
</rdf:Description>
</rdf:RDF>
Note the generated URI http://gensym.org/blankNode1 being used to label the blank node.
Whereas in the abbreviated syntax (omitting namespace declarations) we can express the same graph as:
<rdf:RDF">
<rdf:Description rdf:about=
"http://www.w3.org/Home/Lassila">
<s:Creator>
<rdf:Description>
<s:Name>Ora Lassila</s:Name>
<s:Email>lassila@w3.org</s:Email>
</rdf:Description>
</s:Creator>
</rdf:Description>
</rdf:RDF>
or as:
<rdf:RDF>
<rdf:Description rdf:about=
"http://www.w3.org/Home/Lassila">
<s:Creator rdf:parseType="Resource">
<s:Name>Ora Lassila</s:Name>
<s:Email>lassila@w3.org</s:Email>
</s:Creator>
</rdf:Description>
</rdf:RDF>
or as:
<rdf:RDF>
<rdf:Description rdf:about=
"http://www.w3.org/Home/Lassila">
<s:Creator
s:Name="Ora Lassila"
s:Email="lassila@w3.org"/>
</rdf:Description>
</rdf:RDF>
In most computer programs, the design of output modules is much simpler than the design of input modules. Input design nearly always makes explicit reference to a grammar, a moderately complicated design artifact. Output design, in contrast, is seen as grammatically unproblematic, with effort being reserved only for some beautification features like indentation levels. Many advanced systems often have little more than output templates with slots for the unknowns. Typically, output uses bounded space algorithms such as iterating over a print statement.
A few systems, such as the DOM [31], JSP [29] or Metatool ([9],[10]), provide slightly more sophisticated means of structuring output, but none of these matches the sophistication of parsing technology.
The XML DOM is useful when writing small XML files. The application programmer constructs an appropriate XML Infoset [12] representation of the output, as a DOM tree: the DOM implementation then can serialize this, typically using a recursive style of object oriented programming, making unbounded use of the call stack. We note that such a serialization style does follow a top down application of the XML grammar rules [6], often with one method corresponding to each rule in the grammar. However, the choices available in the grammar are made earlier, during the construction of the DOM tree.
JSP and Metatool each provide their own language for describing the output text. In both, most of the text is simply copied from the output description file into the output stream. The languages include escape mechanisms that permit programming constructs such as loops and function calls to be inserted into the description. When these output description files are compiled (into Java and C respectively), the unescaped text becomes string arguments to print statements, and the escaped control instructions map into the control constructs of the target language. Thus, at a theoretical level, these technologies do not add to the usual model that output is simply print statements wrapped in appropriate control loops. The switch in emphasis, with printing the default and flow-control as marked, is nevertheless very helpful at a practical level. This helps the JSP or Metatool programmer come up with better designed and more intelligible output routines.
The major exception to this generalization that output is unproblematic is in computational linguistics. Here, since the late 80s it has been commonplace ([26], [28], [30]) that generation and parsing are essentially the same, with many systems using the same architecture, the same grammar and the same rules for both. Both the surface textual realization and the deeper semantic representation of the sentence are representations of the sentence and we mediate between the two using the grammar. Both are annotations over the grammar, and have a theoretically similar status [14].
This section and section 5.3 should be omitted by the reader uninterested in theory. The purpose of this section is to further illustrate that generation and parsing are essentially the same.
To explore the insight of computational linguists in more depth, we will employ the universal algebra techniques for describing grammars and languages pioneered by Rus [25].
We will try and keep our use of universal algebra to a minimum, noting [11] as a standard reference.
An algebra has a number of operations over a set. The choice of these operations defines the similarity class of the algebra. Each similarity class has many corresponding algebras, each with the same operations. In object-oriented terms, this similarity class is an interface, and each algebra is an implementation of that interface.
We use four algebras of the same similarity class to define a language. The operations of the algebras correspond loosely to the productions of the BNF grammar of the language. To be precise, each of the operations in the similarity class has a corresponding symbol in the BNF; and at least one production for that symbol with the same arity as the operation. Each production in the grammar has a corresponding operation.
We work with RDF/XML as our example language; and use a very small, simplified fragment of the BNF rules:
rdf : "<rdf:RDF>" objStar "</rdf:RDF>"
objStar :
| obj objStar
The similarity class thus has the three operations rdf/3, objStar/0, objStar/2 (and presumably some for obj as well).
We first define a free algebra Free and a concatenating algebra Surface.
The free algebra corresponds to trees formed using the terms of the BNF, both well formed and ill formed. Here the algebra operates over these trees simply by forming them so that the operation objStar when applied to the arguments X and Y (which are both parse trees) just forms the tree objStar(X,Y). Since ill-formed trees are legal in the free algebra we note that X and Y are not constrained to be an obj and an objStar, in any sense. In the concatenating algebra the operations operate over strings, and every operation concatenates its arguments. Hence any tree in the free algebra when evaluated in the concatenating algebra gives the corresponding string, forming by reading the leaves of the tree. Thus our one well-formed parse tree looks like:
rdf("<rdf:RDF>",objStar(),"</rdf:RDF>")
and evaluates in Surface to the string
"<rdf:RDF></rdf:RDF>".
This process of evaluating a tree from the free algebra in some
other algebra with the same operations is known as a natural
homomorphism, called ![]() .
Thus, we can write:
.
Thus, we can write:

Parsing involves an inverse mapping from a string to a corresponding tree. This tree is required to be well-formed by the grammar. Such well-formedness is defined by a third algebra Rules over the symbols of the grammar in which each operation returns the symbol on the LHS of its corresponding rule if and only if its arguments are the symbols on the RHS of a BNF production corresponding to the operation; otherwise the operation returns ^, an additional failure symbol.
e.g. in Rules the operation objStar/0 always returns objStar, and objStar/2 is defined as:

Thus a parse tree is well formed if and only if when it is evaluated in this third algebra it gives the start symbol of the grammar.
We can write:
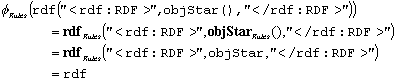
showing the tree to be well-formed.
The fourth and final algebra Deep expresses the 'meaning' of the operations at a deeper level of analysis. In computational linguistics this meaning is expressed as some linguistic structure. In compiler design this meaning is expressed as a partial computation corresponding to that syntactic construct. In RDF/XML that meaning is expressed as a partially formed graph, perhaps with some distinguished nodes. The rdf/3 operation in this algebra returns its second argument, the objStar/0 operation returns the empty graph, and the objStar/2 operation returns the graph merge (see [15]) of its arguments.
Thus the four algebras Free, Surface, Rules, Deep and the
three natural homorphisms ![]() from Free into the other algebras express the grammar.
from Free into the other algebras express the grammar.
Parsing is expressed as given a string s find a meaning d such that there is a tree t and:
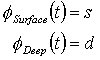
Generation is expressed as given a meaning d find a string s such that there is a tree t and:
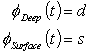
Some parsers choose to build the tree t explicitly; streaming parsers choose not to.
As is well-known the key difficulty with parsing is how to choose which rule to expand at each choice point. The similarity between the definitions for parsing and generation suggest that this too will be the key difficulty in generation, and motivates our use of the word unparsing for grammatically driven generation.
Moreover, the experience of computational linguistics suggests that parsing techniques such as top down left-to-right with backtracking [27], which were developed for parsing, can be applied directly to generation, as long as a little care is taken.
The parsing techniques of computational linguistics are normally found to be excessive for artificial languages. Similarly we may expect all-solution backtracking or chart unparsers to be inappropriate for RDF/XML. Indeed, since the graph of an RDF/XML document puts no constraints on the order of the document, we would expect an all-solutions approach to be unacceptably slow, needing to consider at least a factorial number of different possible orders in its considerations of all serializations.
Instead, we take our inspiration from recursive descent LL(k) parsers3 [22],[23],[24]. These express each grammar rule as a procedure; choice points in the grammar are explicitly represented in the procedures by lookahead code. The lookahead code uses the leftmost section of the unmatched input string to decide which possible rule best matches and hence on the flow of control of the parser. A possible way of structuring such code, for say an LL(1) parser, is to use a boolean guard on each of the rule procedures. The guard inspects the lookahead token: if it is not an acceptable left-most token for that production then false is returned, otherwise the parser commits to that production and the guard returns true. Hence, at a choice point where either t1 or t2 are acceptable tokens we can use code like:
if (t1Guard()) t1(); else if (t2Guard()) t2(); else error();
to exercise the choice. If the lookahead is acceptable to rule
t1 then t1Guard() will return true, firing t1(), otherwise
t2Guard() will inspect the lookahead. If the lookahead is not
acceptable to rule t2 , then error() will be invoked.
The guards are often defining by computing the follow set (see [1]). Alternatively the guards may invoke each other in the same pattern by which the rules and the procedures invoke each other. In this case, duplication of the logic is avoided by combining each guard with its procedure, to give a single Boolean function that either returns false, if the guard fails, or returns true and matches the rule. This combined function allows the code snippet above to be expressed more compactly as :
t1()||t2()||error();
For an unparser we hence use the following design pattern.
Each grammar production has a corresponding rule procedure and a guard.
The guard determines whether to use this production or not. This evaluation is done on the basis of that part of the graph that has not yet been serialized. If the rule is not appropriate no output is generated and false is returned. Otherwise the unparser commits to the rule.
This design pattern puts a significant burden on the guards, since the choices made are irrevocable. For RDF/XML this is preferable to the alternative burden of a non-deterministic framework for unparsing in which backtracking (or equivalent non-deterministic techniques) allows explicit consideration of alternatives.
The term deep structure was introduced in section 4. It is borrowed from computational linguistics to indicate the 'meaning' of a derivation tree at some level of abstraction. In RDF/XML this corresponds to partially formed graphs, perhaps with some distinguished nodes.
During parsing the input string is divided into sections each of which matches some subtree licensed by the grammar. Similarly during unparsing we divide the deep structure matching each tree up into parts that match the various subtrees. Some aspects of this division is done before the rule is invoked, some during rule invocation.
As an example, take the deep structure of an objStar production to be a graph, and the deep structure of an obj production to be a pair consisting of a graph and a distinguished node. Suppose we have a graph g that we wish to expand as an objStar then we have:
objStar : obj objStar
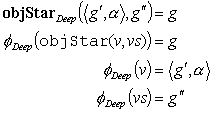
That is the graph g corresponding to the LHS of
the grammar rule is formed as an appropriate combination of the
pair ![]() and
and ![]() , where the obj subtree v
corresponds to the graph and distinguished node
, where the obj subtree v
corresponds to the graph and distinguished node ![]() , and the remaining objStar subtree
corresponds to the graph
, and the remaining objStar subtree
corresponds to the graph ![]() . This
appropriate combination is a graph merge, tidied as in the Model
Theory [15].
. This
appropriate combination is a graph merge, tidied as in the Model
Theory [15].
To generate this using top down recursive descent, we are given
g and we choose a particular node α in
g. While we expand the (unknown) obj subtree v for
this a we will find some subgraph g' of g
rooted in a which corresponds to the subtree. We then take the
graph difference of g and g' to continue
expanding the objStar subtree vs using ![]() as the given
graph.
as the given
graph.
While it is necessary to make some explicit choices, for example the choice of a, it is not necessary to make explicit all the nested choices before starting on some production.
The single most significant grammatical constraint in RDF/XML output is the desire not to label blank nodes. We note that in the Model Theory [15] that blank nodes have a different semantics from a labelled node. There is no standard way of distinguishing a local identifier for a blank node from a URI for a non-blank node. Hence high-quality RDF/XML output should not label blank nodes in the XML.
The example in section 2.3 shows a blank node in a graph. The first serialization given (in the basic serialization) used a generated URI to label it. The other serializations used the abbreviated syntax to avoid this.
Unfortunately, the grammar does not permit all blank nodes in all graphs to be unlabelled in the XML. Unlabelled nodes of the RDF/XML serialization can only be the object of a single triple4.
Thus RDF/XML generation starts with an initial pass over the graph to identify blank nodes that can remain blank: those that, excluding reification, are not the object of more than one triple. It is also necessary to distinguish those that are the object of one triple from those that are not the object of any triple.
We have already seen the top-level grammar rules for RDF, (now in EBNF [17]):
rdf : "<rdf:RDF>" obj* "</rdf:RDF>"
Some other productions that are relevant to the discussion of blank nodes include:
obj : description | typedNode
description : "<rdf:Description"
idAboutAttr? propAttr* ">"
propertyElt*
"</rdf:Description>"
propertyElt : "<" propName ">" obj "</" propName ">"
Excluding reification, the distinguished node of the obj's in the top-level production, if blank, only occur as the subject of triples in the graph. Hence if we choose a blank node a as the distinguished node for an obj in the obj*, and a occurs as the object of some triple, then we must assign it a label (a URI) before serializing it. Otherwise we will be unable to refer to it in any subsequent occurrence specifically when we serialize the triple of which it is the object.
The only other occurrence of the obj symbol on the RHS of a production is in the property element production shown5, where the distinguished node of the obj production becomes the object of a triple. The argument concerning the blank node a is also applicable to this other instance of the obj symbol. Whenever we are serializing a blank node b that occurs as the object of two or more triples in the graph, triggered by this propertyElt production, then we must assign it a URI before serializing it. Otherwise we will be unable to refer to it in any subsequent occurrence specifically when we serialize the second triple of which it is the object.
Thus it is desirable to only use the top-level production for nodes in the graph that are either labelled with a URI or not the object of exactly one triple.
Since not all graphs can be serialized in RDF/XML without giving identifiers to some blank nodes, it has to be acceptable (if undesirable) for the RDF/XML serializer to do this.
The rdf:ID attribute and the rdf:about attribute both assign a
URI [4] label to the only node in
the (trivial) graph corresponding to the idAttr and the aboutAttr
productions in the grammar. The difference is that the URI
corresponding to an rdf:ID attribute must be a fragment ID of the
base URI of the output stream, which matches the NMToken production
from the XML specification [6].
We will refer to this constraint on a URI as the ID
constraint.
The RDF/XML syntax has a compact form for representing the reification of most triples. This reification is four triples with the same subject, the reification resource. This compact form can represent one such reification resource as long as its URI satisfies the ID constraint. Hence, in the guard for the reification rule it is necessary to check whether these all hold for the triple of the parent propertyElt production.
In order to force the use of reification, it is necessary to avoid choosing such nodes during the top-level expansion of the objStar rule (see section 5.3), and to avoid explicitly expanding the reification quad, if the reification node occurs as an obj(ect) of a property element production.
The rdf:bagID attribute is another peculiarity of RDF/XML
syntax. It is very powerful, matching a complex subgraph, but very
specific. It causes all the triples in a particular subgraph to be
reified, and creates an rdf:Bag consisting of a named resource and
edges linking it to each of the reifications. It generates a large
number of triples, each with its own particular constraints, e.g.
the node which is the center of each reification quad must be
either unlabelled or labelled with the constraints identified above
in section 6.2.
The guard to match the bagIdAttr production then has knock on effects, since once we have decided to use the bagIdAttr production then no triples that do not have their reification in the bag may be produced.
RDF/XML allows the use of a container membership pseudoproperty
rdf:li. This expands to rdf:_1, rdf:_2 etc.
Based on the liberal reading of this production suggested by the RDF Core Working Group [21], this can be treated with a single additional variable to count where we have got to.
Each property element production starts by trying to choose a triple to match that does match rdf:_N where N is the current value of the counter. If this guard succeeds, then other triples are not considered and an rdf:li property element is generated.
Given an RDF/XML graph with a container with a hole, e.g. Figure 2
The above technique will use the rdf:li pseudoproperty before
the hole, because the guard will succeed. At the hole the guard
fails and the remaining edges will be serialized using the property
element productions.
This results in the following XML (omitting namespace declarations):
<rdf:RDF>
<rdf:Description
rdf:about="http://x.org/packages/X11">
<s:DistributionSite>
<rdf:Alt>
<rdf:li rdf:resource="ftp://ftp.x.org"/>
<rdf:_3 rdf:resource="ftp://ftp.eu.net"/>
</rdf:Alt>
</s:DistributionSite>
</rdf:Description>
</rdf:RDF>
The code in Jena 1.2 is based on a stricter reading of Model
& Syntax [19] in which the
whole container production is guarded by the requirement that the
only properties on the container are its type and a single
consecutive sequence, starting at rdf:_1 of container membership
properties. With the example in Figure 2
the hole prevents the use of the container production, and a typed
node construction is used instead. In this the rule for the rdf:li
pseudoproperty is not legal, so both container membership arcs are
shown with their full property names:
<rdf:RDF>
<rdf:Description
rdf:about="http://x.org/packages/X11">
<s:DistributionSite>
<rdf:Alt>
<rdf:_1 rdf:resource="ftp://ftp.x.org"/>
<rdf:_3 rdf:resource="ftp://ftp.eu.net"/>
</rdf:Alt>
</s:DistributionSite>
</rdf:Description>
</rdf:RDF>
The rdf:aboutEach distributed subject construction is another
peculiarity that requires as special attention during generation as
during parsing. Each statement with an rdf:aboutEach identifying
its subject rather than an rdf:about or rdf:ID corresponds to many
triples, one for each member of the container identified by the URI
which is the value of the rdf:aboutEach attribute.
Given its file scope, the triples that qualify for rdf:aboutEach
must be identified before any other choice during generation. Like
with the rdf:bagID construction this production corresponds to a
large number of triples and it is tedious but necessary to check
that all of them are present in the graph to be serialized.
Having identified triples that are suited for treatment with
rdf:aboutEach they are serialized first so that all embedded
triples are identified.
The primary motivation for generating abbreviated RDF/XML is human readability. Hence pragmatic considerations are also important when serializing.
The abbreviated syntax includes abbreviations for string valued property attributes, as long as the value can be expressed as an XML normalized attribute value. These are good for shorter string values.
When a node of the graph is an object of a triple, if all its properties can be expressed as property attributes then it may be appropriate to use the compact property element production
propertyElt : "<" qname idRefAttr? bagIdAttr? propAttr* "/>"
for this triple. Again this is implemented by putting a complex guard on this particular production.
This production was used for the Creator property in the final serialization of the example from Figure 1, i.e:
<rdf:RDF>
<rdf:Description rdf:about=
"http://www.w3.org/Home/Lassila">
<s:Creator
s:Name="Ora Lassila"
s:Email="lassila@w3.org"/>
</rdf:Description>
</rdf:RDF>
We see that the string values “Ora Lassila” and “lassila@w3.org” both were appropriately short and compatible with XML attribute value normalization rules and so the compact form is both possible and elegant.
It is difficult to follow XML that is too deeply embedded. Having an arbitrary limit to embedding is suggested.
In many of the applications of RDF there is a preference for not embedding some elements. E.g. in RDF Schema [7] and DAML [16] it is preferred to list properties and classes as top-level elements rather than having an embedded description of one within the description of some other property or class.
The grammar permits the triples to be in any order. It is, however, conventional to group all triples with the same subject as child property elements or attributes of the same description node.
Moreover the use of the container membership production rdf:li requires the conventional ordering of the container membership triples.
Some subdialects of RDF have a distinct stylistic preference for
certain ordering rules at both the top-level and lower down. E.g. a
typical DAML [16] file starts
with <daml:Ontology rdf:about="">.
All these ordering features are implemented in Jena by an
appropriate division of the graph to be serialized on the relevant
rule invocations (c.f. section 5.3).
For example, the rule for objstar used in the top-level expansion
selects the next object to be serialized according to a (user
modifiable) list of types starting with daml:Ontology.
If the graph contains a directed loop of blank nodes each of which is the object of exactly one triple then the top-level guard suggested in section 6.1 will not permit the serialization of this loop.
The approach taken within the Jena RDF/XML writer is to be optimistic and hope that the whole graph will serialize despite that rule, i.e. that there are no instances of such directed cycles.
The case when the graph has not been fully serialized yet no further triple is permitted past the guard is dynamically detected. This optimism was ill founded: in response, one arbitrary triple is permitted past the guard. This should permit the whole cycle to be written out.
A full implementation of an RDF/XML serializer should be readily customizable for the various RDF subdialects like RDF Schema [7], DAML [16], CC/PP [18], RSS [3], PRISM [13]. Each of these either explicitly or implicitly uses only a subset of the full RDF/XML grammar. Also the pragmatic rules may have a different force with each.
Hence customizability includes8:
Many of the choices expressed in the guard expressions require a search through the whole graph for matching edges. We take this search to be O(n). The number of times such choices need to be made is also proportionate to the size of the graph (n being the number of edges in the graph). Hence this too is O(n) suggesting an overall complexity of O(n2).
The decision as to whether to use rdf:aboutEach involves taking the intersection of the members of every container in the graph. This has similar overall complexity.
The reification productions (including rdf:bagID) have particularly complicated rules associated with them. From the viewpoint of generation the conditions on these rules are even more baroque than they appear when parsing. This presents significant difficulty both for automatic generation and human generation of RDF/XML that uses these productions.
The rdf:aboutEach production also presents unique processing difficulties.
Given these difficulties it is arguable that an RDF/XML generator should avoid all these productions regarding them as misguided.
RDF/XML is a surprisingly complicated syntax. It is replete with choices: a serializer that is aware of the choice points and makes good choices at each produces substantially clearer output than one that doesn't. Many of these choices are governed by arbitrary and capricious constraints that must be understood by the generator. A new design pattern in which each grammar rule has a corresponding procedure guarded by a Boolean function that assesses its appropriateness has been shown to be applicable to this problem.
Thanks to the anonymous referees for their comments, advice and corrections.