The limits of Web metadata, and beyond

Abstract

The World Wide Web currently has a huge amount of data, with practically no classification information, and this makes it extremely difficult to handle effectively. It has been realized recently that the only feasible way to radically improve the situation is to add to Web objects a metadata classification, to help search engines and Web-based digital libraries to properly classify and structure the information present in the WWW. However, having a few standard metadata sets is insufficient in order to have a fully classified World Wide Web. The first major problem is that it will take some time before a reasonable number of people start using metadata to provide a better Web classification. The second major problem is that no one can guarantee that a majority of the Web objects will be ever properly classified via metadata. In this paper, we address the problem of how to cope with such intrinsic limits of Web metadata, proposing a method that is able to partially solve the above two problems, and showing concrete evidence of its effectiveness. In addition, we examine the important problem of what is the required "critical mass" in the World Wide Web for metadata in order for it to be really useful.

Keywords

Metadata; Automatic classification; Information retrieval; Search engines; Filtering

1. Introduction

However, usage of metadata presents the big problem that it does not suffice to have some standard metadata sets in order to have a fully classified World Wide Web. The first major problem is that a long time will pass before a reasonable number of people will start using metadata to provide a better Web classification. The second big problem is that none can guarantee that a majority of the Web objects will be ever properly classified via metadata, since by their nature metadata:

• are an optional feature
• they make heavier the writing of Web objects
• their usage cannot be imposed (this is necessary to ensure HTML backward compatibility)

In this paper, we address the problem of how to cope with such intrinsic limits of Web metadata. The main idea is to start from those Web objects that use some form of metadata classification, and extend this information thorough the whole Web, via suitable propagation of the metadata information. The proposed propagation technique relies only on the connectivity structure on the Web, and is fully automatic. This means that

1. it acts on top of any specific metadata format, and
2. it does not require any form of ad-hoc semantic analysis (which can nevertheless be smoothly added on top of the propagation mechanisms), therefore being completely language independent.

The method is applied to a variety of tests. Although, of course, they cannot provide a complete and thorough evaluation of the method (for which a greater number of tests would be needed), we think they give a meaningful indication of its potential, providing a reasonably good first study of the subject.

In the first general test, we show how the effectiveness of a metadata classification can be enhanced significantly. We also study the relationship between the use of metadata in the Web (how many Web objects have been classified) and the global usefulness of the corresponding classification. This enables also to answer questions like what is the "critical mass" for general WWW metadata (that is to say, how much metadata is needed in an area of the Web in order for it to be really useful).

Then, we present another practical application of the method, this time not in conjunction with a static metadata description, but with a dynamic metadata generator. We show how even a poorly performing automatic classifier can be enhanced significantly using the propagation method.

Finally, we apply the method to an important practical case study, namely the case of PICS-compliant metadata, that allow parents to filter the Web from pages that can be offensive or dangerous for kids. The method is shown to provide a striking performance in this case, thus showing to be already directly applicable with success in real-life situations.

2. Fuzzy metadata

3. Back-propagation

3.1. Combining information

The solution to these issues is not difficult. One case is easy: if the attributes are different, then we simply merge the information. For instance, if we calculate via back-propagation that a Web object has the metadatum A:v and also the metadatum B:w, then we can infer that the Web object has both the metadata, i.e. it can be classified as "A:v, B:w". The other case is when the attributes are the same. For instance, we may arrive to calculate via back-propagation that a Web object has attributes A:v (this metadatum back-propagated by a certain Web object) and A:w (this metadatum propagated by another Web object). The employed solution is to employ fuzzy arithmetic and use the so-called fuzzy or of the values v and w, that is to say we take the maximum value between the two. So, O would be classified as A:max(v,w) (here, max denotes as usual the maximum operator). This operation directly stems from classic fuzzy logic, and its intuition is that if we have several different choices for the same value (in this case, v and w). then we collect the most informative choice (that is, we take the maximum value), and discard the other less informative values. Above we only discussed the case of two metadata, but it is completely obvious how to extend the discussion to the case of several metadata, just by repeatedly combining them using the above operations, until the final metadatum is obtained.

As a technical aside, we remark how the above method can be seen as a "first-order" approximation of the back-propagation of the so-called hyper-information (see [8]); along the same line, more refined "higher-order" back-propagation techniques can be built, at the expense of computation speed.

4. Testing

Suppose to have a region of Web space (i.e. a collection of Web objects), say S; the following process augments it by considering the most proximal neighbourhoods:

Consider all the hyperlinks present in the set of Web objects S: retrieve all the corresponding Web objects and add them to the set S.

As an aside, note we are overlooking for the sake of simplicity some implementation issues that we had to face, like for instance: checking that no duplications arise (that is to say, that the same Web object is not added to S more than once); checking that we have not reached a stale point (in some particular case, it may happen that the Web objects in S have only hyperlinks to themselves, and so the augmentation process does not increase the size of S); cutting the size of S exactly to the bound n (the augmentation process may in one step significantly exceed n).

So, in order to extract a region of the Web to work with, the following process is used:

1. A random Web object is chosen (to this aim, we have employed URouLette).
2. It is augmented repeatedly using the aforementioned technique, until a Web region of the desired size n is reached.

4.1. Experimentation

We did several tests to verify the effectiveness of the back-propagation method, and also in order to decide what was the best choice for the fading factor f. Our outcome was that good performances can be obtained by using the following rule-of-thumb:

Intuitively, this means that when the percentage of already classified Web objects is low (p very low), then we need a correspondingly high value of f (f near to one), because we need to back-propagate more and we have to ensure that the fading does not become too low. On the other hand, when the percentage of already classified Web objects becomes higher, we need to back-propagate less, and so the fading can be kept smaller (in the limit case when p=1, the rule gives indeed that f=0, that is to say we do not need to back-propagate at all).

Even if our personal tests were quite good, our evaluations could be somehow dependent on our view of judging metadata. Moreover, besides confirmations on the effectiveness of the approach, we also needed more large-scale results analyzing in detail the situation with respect to the percentage p of already classified Web objects.

Therefore, we performed a more challenging series of tests, this time involving an external population of 34 users. The initial part of the tests was exactly like before: first, a random Web object is selected, and then it is increased until a Web region of size n is reached. Then the testing phase occurs: we randomly choose a certain number m of Web objects that have not been manually classified, and let the users judge how well the calculated classifications describe the Web objects. The "judgment" of a certain set of metadata with respect to a certain Web object consists in a number ranging from 0 to 100, with the intended meaning that 0 stands for a completely wrong/useless metadata, while 100 for a careful and precise description of the considered Web object.

It is immediate to see that in the original situation, without back-propagation, the expected average judgment when p=n% is just n (for example, if p=7%, then the average judgment is 7%). So, we have to show how much back-propagation can improve on this original situation.

As said, for the tests we employed a population of 34 persons: they were only aware of the finalities of the experiment (to judge different methods of generating metadata), but they were not aware of our current method. Moreover, we tried to go further and to limit every possible "psychological pressure", clearly stating that we wanted to measure the qualitative differences between different metadata set, and so the absolute judgment was not a concern, while the major point was the judgment differences.

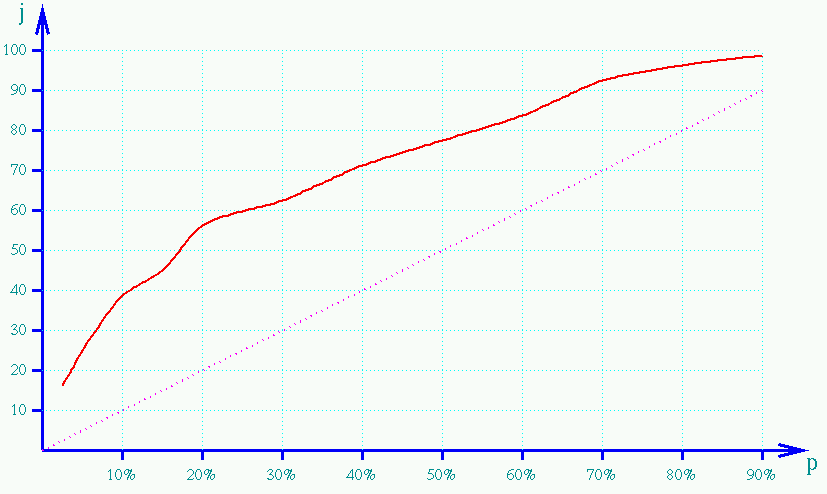
The first round of tests was done setting the size n of the Web region to 200, and the number m of Web objects that the users had to classify to 20 (which corresponds to the 10% of the total considered Web objects). Various tests were performed, in order to study the effectiveness of the method with the varying of the parameter p. We run the judgment test for each of the following percentages p of classified Web objects: p=2.5%, p=5%, p=7.5%, p=10%, p=15%, p=20%, p=30%, p=40%, p=50%, p=60%, p=70%, p=80% and p=90%. The final average results are shown in the following table:

 

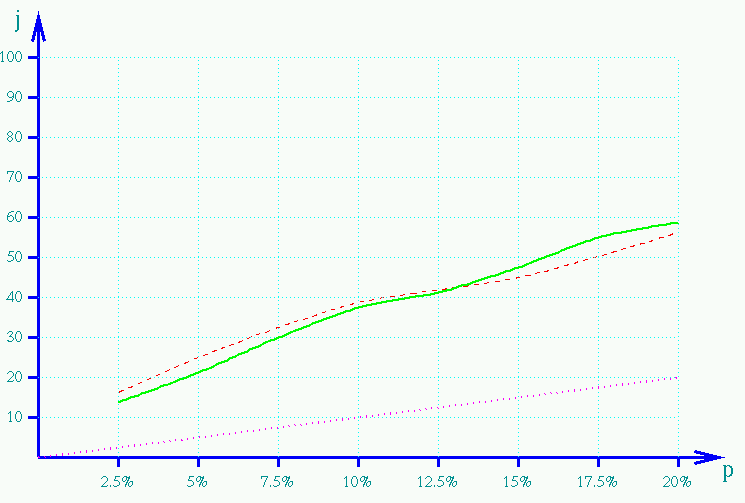
As we can see, there is an almost linear dependence roughly from the value of p=20% on, until the value of p=70% where the judgment starts its asymptotic deviation towards the upper bound. The behaviour is also rather clear in the region from p=5% to p=20%: however, since in practice the lower percentages of p are also the more important to study, we run a second round of tests specifically devoted to this zone of p values. This time, the size of the Web region was five times bigger, setting n=1000, and the value m was set to 20 (that is to say, the 2% of the Web objects). Again, various tests were performed, each one with a different value of p. This time, the granularity was increased, so that while in the previous phase we had the values of p=2.5%, p=5%, p=7.5%, p=10%, p=15%, p=20%, in this new phase we also run the tests for the extra cases p=12.5% and p=17.5%, so to perform an even more precise analysis of this important zone. The final average results are shown in the next table:

Therefore, the results we have obtained show that:

• When employing a particular metadata classification for the Web, even when the percentage of classified Web objects is relatively small, usage of the back-propagation method can significantly help the effectiveness of the classification, thus helping the metadata to get more and more widespread, especially in the initial crucial phases when the number of classified objects will be extremely limited.
• The experimentation can help to answer the fundamental question: what is the minimum "critical mass" that a general WWW metadata classification needs to reach in order to be really useful? If we fix the level of decency of metadata to a judgment level of 50, then by reverse interpolation we obtain that a reasonable prediction for the critical mass is roughly 16%. Thus, in order for a general WWW metadata classification to be really useful, at least 16% of the WWW (or of the local WWW zone we are considering) should be classified. Note that, without back-propagation, the critical mass would grow up to 50%.
• Analogously, we can predict what is the percentage metadata needs to have in order to reach an "excellence level": if we fix such a level at 80, then by reverse interpolation we obtain a value of 53%; so, using the back-propagation method we can reach an excellence level when slightly more than half of the WWW (or of the local WWW zone we are considering) has been classified.

• Before the critical mass is reached, there is roughly a linear dependency between the percentage of metadata and its usefulness (as given by the judgment) with a linear factor of 3 (i.e., as soon as p increments, the usefulness increases three times faster);
• After the critical mass is reached, and until the value of p=70%, there is roughly a linear dependency between the percentage of metadata and its usefulness (as given by the judgment) with a linear factor of 0.6; so, this time usefulness increases slower (slightly more than at half speed) as the percentage of metadata increases;
• After the value of p=70%, we have an even slower linear dependency with the value of roughly 0.3.

5. Automatic classification

the ratio between the number of words in the document that are representative keywords of A, and the total number of words in the document.

¹/₁₀ of the the number of words in the document that are representative keywords of A, with the provisos that:

1. Each word contained in a Heading or Title header counts twice
2. If the final number of words exceeds 10, then set it to 10.

We have again conducted a test to measure the quality of the obtained metadata, employing the same population of 34 persons employed in the first experiment. The test was conducted much in the same way: again, we built various Web regions of size n=200. Now, however, since we have an automatic classifier we are not limited any more to classify a minor part of the Web region: so, we run the automatic classifier on the whole Web region. Again, the users were asked to judge the quality of the obtained metadata, just like in the previous experiment, on a random sampler of n=20 Web objects. The test was repeated 10 times, each time with a different Web region. The final average quality judgment was 43.2.

Then, we did the same tests, but this time we used the back-propagation method on the metadata obtained by the automatic classifier. The final outcome was: the average quality judgment jumped to 72.4 (in nice accordance with the interpolation results obtained in the previous experiment!).

6. PICS and parental control

PICS-based metadata suffer even more from the wide applicability problem, since they essentially require a trustworthy third party (the label bureau) to produce the content rating (this is a de facto necessity, since user-defined local metadata are obviously too dangerous to be trusted in this context). And, indeed, already at the present moment there have been many criticisms on the capability of such third parties to survey a significant part of the Web (see e.g. [12]). The adopted solution is to limit Web navigation only to trusted refereed parts, but again this solution has raised heavy criticisms in view of the same argument as before, since this way a huge part of the Web would be excluded.

Therefore, we have employed the back-propagation method in order to enhance a publically accessible filtering system, namely the aforementioned NetSheperd. NetSheperd has acquired a somehow strategical importance in view of its recent agreement with Altavista to provide filtered-based search. NetSheperd offers online its filtered search engine. So, we have employed this tool as a way to access the corresponding metadata database, and generating metadata for a corresponding Web object.

The test was conducted as follows. First, we chose 10 Web objects that would be clearly be considered at a dangerous level by any rating system. The choice was done by taking the top 10 entries of the Altavista response to the query "nudity". Analogously to the previous experiments, we built from these Web objects the corresponding Web regions of size n=50. Then, we used the NetSheperd public filtering system to provide suitable metadata for the Web objects. It turned out that 32% of the Web objects were present in the database as classified, while all the remaining 68% of Web objects were not. Soon afterwards, we run the back-propagation method on the Web regions. Finally, again, we asked the population of 34 users to judge (with m=20) the obtained classifications in the perspective of a parental accessibility concern. The final average judgment was 96.4, and the minimum rating was 94: in a nutshell, all the generated metadata perfectly matched the expectations. It is interesting to note that the Web regions were not exclusively composed of inherently dangerous material: among the Web objects the users were asked to classify, a few were completely kids safe, and indeed they have been classified as such by the back-propagation.

The exceptionally good performance of the back-propagation in this case can be explained by the fact that we were essentially coping with an ontology composed by one category. In such situations, the performance of the back-propagation is very good, since the only uncertainty regards the fuzzy value of the attribute, and not the proper classification into different, possibly ambiguously overlapping, categories.

7. Conclusions

References

[2] Caplan, P., You call it Corn, we call it syntax-independent metadata for document-like objects, The Public-Access Computer Systems Review 6(4), 1995.

[3] Deatherage, M., HotSauce and meta-content format, TidBITS, 25 November 1996.

[4] Dublin Core Metadata Element Set, 1997.

[5] Hardy, D., Resource Description Messages (RDM), July 1996.

[6] Lagoze, C., The Warwick framework, D-Lib Magazine, July/August 1996.

[7] Library of Congress, Machine-readable cataloging (MARC).

[8] Marchiori, M., The quest for correct information on the Web: hyper search engines, in: Proc. of the 6th International World Wide Web Conference (WWW6), Santa Clara, California, U.S.A., 1997, pp. 265–276; also in: Journal of Computer Networks and ISDN Systems, 29: 1225–1235, Elsevier, Amsterdam, 1997.

[9] Miller, P., Metadata for the masses, Ariadne, 5, September 1996.

[10] The World Wide Web Consortium (W3C), Platform for Internet content selection.

[11] Web Developers Virtual Library, META tagging for search engines.

[12] Weinberg, J., Rating the Net, Communications and Entertainment Law Journal, 19, March 1997. 

Vitae