|
|||
Network and Service Management Research,
Bell Labs, Lucent Technologies,
Holmdel, NJ 07733-3030, U.S.A.
pk@research.bell-labs.com and
sugla@research.bell-labs.com
Conceptually, co-operation between proxies is a simple concept. It is based on the premise that it should be quicker and cheaper to find an object in another proxy's cache within an intranet rather than access the Internet server hosting the object. However, there are important issues in co-operation. Objects from another proxy must be retrieved as quickly as possible. Methods to co-operate and manage this co-operation introduce complexity into the system; caches should co-operate only if there is a performance gain from it.
The question of how to reduce the time taken for servicing requests by a co-operating proxy has been studied by other researchers [1, 3, 4]; we do not tackle that issue here. The Harvest object cache [1] was the first system designed to operate in concert with other instances of itself. It used unicasting for achieving co-operation. Malpani et al. [4] have presented a multicasting-based technique to reduce the time it takes for communication between caching proxies. Gadde et al. [3] consider an approach of maintaining a centralized database of pages existing in various caches.
Our goal in this paper is orthogonal to the issue of getting to a page in a co-operating proxy's cache quickly. We are interested in experimentally analyzing the benefit provided by co-operation. To the best of our knowledge, there are no results that quantify the actual advantage gained by co-operation between intranet proxies. There are some simulation results presented in [3] describing benefits of shared caches. However, these results demonstrate the benefit of having proxy caches, not the effect of proxy caches co-operating with each other. Other works (e.g., in [10]) look at issues in hierarchical cache systems. From that point of view, we are evaluating intranets with Squid-like proxies [11] at the bottom of the hierarchy that co-operate to maximize benefit.
From a conceptual standpoint, performance improvements due to co-operation come about for similar reasons to what make proxies popular. Apart from increasing the effective size of cache, we can leverage from what we call virtual prefetching. That is, a user accessing object i through proxy X is effectively prefetching the object for a user who will access object i in the future through another co-operating proxy Y.
For our study, we concentrate on isolating the virtual prefetching aspect of the performance improvement and look at the effect of co-operation on each proxy separately. We observe that byte hit rate improvement due to virtual prefetching can vary from as low as 0.7% to as high as 28.9%. We try to understand the factors that affect this improvement, and in particular, study the effect of community size. We quantify the overhead due to co-operation on network traffic and server load. We observe that, depending on the co-operation technique and architecture, about 7.5% of the extra requests created by proxies can be satisfied, and server load can increase from 10–300%. This indicates that co-operation should be done with care. We infer policies that proxies should follow to request data from other proxies or entertain requests from other proxies. Another contribution of our work is to emphasize that proxies should monitor the correct variables and provide hooks for use of these monitored variables for performance and configuration management. This is particularly important with more vendors now adopting the Internet Cache Protocol (ICP) [6] to provide inter-cache communication abilities.
In Section 2, we present the methodology for our study. We present our results in Section 3. Based on these results, in Section 4 we make inferences that will aid in deciding when and how intranet proxies should co-operate, and briefly describe our ongoing work. We conclude in Section 5.
We considered 11 consecutive days of data from these proxy logs. A brief summary of some information about the logs is given in Table 1.
The "#IP end-points" column specifies the number of hosts that are connected to the network served by the proxy server. (There may be no Web accesses from many of these end-points.)
The last three columns are derived from the logs. The "#Unique accessors" specifies the actual number of unique IP hosts that accessed the proxy server over the course of the 11 days. The "#Accesses" column specifies the number of URL requests received by the proxy. The "Cache needed" column specifies the amount of cache that would have accommodated all the requests for that proxy, with no replacement required in cache. That is, a cache with the space as specified in that column qualifies as an infinite cache for all practical purposes.
We studied two protocols for co-operation: symmetric and asymmetric. We say that proxy x is "bigger than" proxy y if proxy x supports more clients than proxy y; we denote this relationship by x > y. (We assume that the proxies are configured so that the number of hosts they serve is in proportion to their "capacity".) Based on Table 1, we see that B > M > S. (The symbols for the three proxies have been chosen to stand for "Big", "Medium", and "Small", respectively, for easier reference through the paper.). In a symmetric protocol, a co-operation between proxy servers X and Y implies that every miss by proxy X is requested from proxy Y and vice-versa. To achieve this, we parsed the logs of the co-operating proxies based on time of access, and assumed that the clocks on these machines were synchronized. We assumed a hit if either of the two caches could have serviced the request. If an object was serviced from another proxy's cache, the local copy was updated. This update assumption will not affect our reported numbers for the hit rate improvements due to co-operation, but will reduce our network load numbers. Some proxy servers [11] support the idea of not maintaining a local copy if the peer is easily accessible. With an asymmetric protocol, a miss by proxy X is requested from proxy Y only if Y > X.
We studied each proxy acting independently (i.e., B, M, and S, separately), all three pairs of co-operation (i.e., B+M, B+S, and M+S), and the case when all three proxies co-operated (i.e., B+M+S).
| No co-op. | B+S | M+S | B+M | B+M+S |
|---|---|---|---|---|
| 30.16 | 31.24 | 30.36 | 31.92 | 33.08 |
However, a more informative assessment is to study the impact of co-operation on each proxy individually. The hit rate improvements for the three proxies when considering bytes transferred and number of requests are shown in Table 3.
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The numbers reported in these tables are based on the entire 11 days of data. Recall that the hit rate for proxy p in asymmetrically co-operating with other proxies is equivalent to the hit rate obtained for p by symmetrically co-operating with just those q where q > p.
We observe that even with symmetric co-operation, the hit rate improvements are most pronounced for the smaller proxy (S), and virtually non-existent for the largest proxy (B). This is not too surprising, since the proxy serving a larger number of hosts is likely to see different URLs requested and will then be in a position to serve these pages from its local cache. It is interesting to compare the hit rate numbers without co-operation (i.e., the hit rate numbers under the "none" column in Table 3) with comparable studies of hit rate numbers from [3, 7]. Our hit rate numbers are closer to the ones reported in [3] and lower than the ones reported in [7]. This is due possibly to two reasons. First, there seems to be a difference in locality of access between universities (as in the study in [7]) and corporations (as in the study in [3] and here). Second, the access patterns have also been changing over the past few years, with more dynamically generated objects in user requests; the study in [7] was performed with earlier data than our study here.
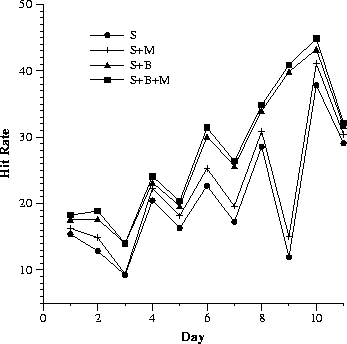
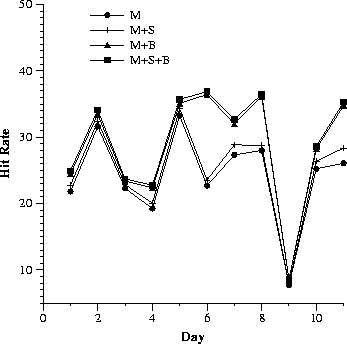
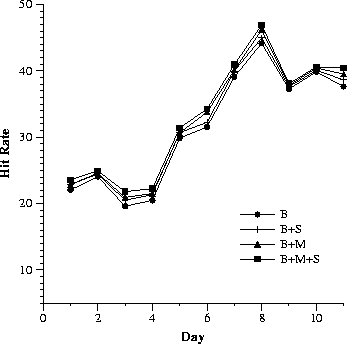
Since it is well known that Web traffic varies with the day of the week and also within each day, we try to get a finer granularity for reporting hit rates. In Fig. 1, we depict for each proxy server and for each day, the computed hit rate for requests made to the proxy server for that day, with and without co-operation.
 |
 |
|||||||||||||||||||||
| (a) Proxy: S | (b) Proxy: M | |||||||||||||||||||||
 |
| |||||||||||||||||||||
| (c) Proxy: B | (d) Hit rate improvements | |||||||||||||||||||||
While the general observation still stands (that the smaller proxy has the maximum benefit from co-operation), we make a couple of other interesting observations. It is well-known that hit rates are better with warmer caches. In our case, since most of the significant hit rate improvements due to co-operation are in the later days when the cache is warm, we might infer that co-operation with a warmer cache is also more beneficial. Hit rate improvements in co-operation with B, the cache with the largest set of users, is maximum. The impact on S in co-operating with both B and M is virtually identical to co-operating with B alone. This suggests that indiscriminate co-operation is not a good policy. This issue will be attacked in more detail in subsequent subsections. The significant variation in benefit from co-operation over the days implies the importance of online monitoring and management of co-operation.
We calculate the increase in traffic as the extra number of requests generated due to co-operation. By definition, the extra traffic created by proxy p is the number of misses by p when it is in stand-alone mode multiplied by the number of proxies that it queries. The extra traffic on the network is the sum over all proxies of the extra traffic created by each proxy. We define the percentage of useful traffic generated by proxy p as the ratio of the number of requests generated by p that are served by another proxy to the extra traffic created by proxy p. The percentage of useful traffic for the network is defined to be the ratio of the total increase in the number of hits (taken over all proxies) to the extra traffic on the network.
|
|
|||||||||||||||||||||||||||||||||||||||
In Table 4a we evaluate for each proxy, the percentage of useful extra traffic generated by the proxy. To understand the table better, consider the 4.24% number corresponding to the (S,M) entry. It implies that if proxies S and M co-operate, then 4.24% of the requests created by proxy S for M (due to co-operation) result in hits. This gives a handle on whether S should co-operate with M or not. We observe that, relatively speaking, proxy B is not generating too much useful co-operation traffic. However, when S and M co-operate with B, they create more useful extra traffic. The last column also suggests what we intuitively noted in Section 3.1: Full co-operation in this case is not as useful as just co-operating with B. We also observe that asymmetric co-operation is better than symmetric co-operation from the point of view of usefulness.
Table 4b illustrates from the network's point of view as to how much useful traffic is generated for both symmetric and asymmetric protocols. We note that for the symmetric case, the numbers are uniformly low and there is not a substantial difference between the various co-operating architectures. The asymmetric case is uniformly better than the symmetric case.
| Loc. | Configurations | |||
|---|---|---|---|---|
| B+S | M+S | B+M | B+M+S | |
| S | 202.85% | 97.58% | – | 300.43% |
| M | – | 44.92% | 129.66% | 174.58% |
| B | 10.43% | – | 14.48% | 24.91% |
Notice that the number in the last column will be the sum of the numbers in the previous columns. The corresponding numbers for asymmetric co-operation are obtained from Table 5 by observing that there is no extra load on a smaller server in co-operating with a larger server.
We observe that the larger proxy B does not see an appreciable increase in its load due to co-operation. With symmetric co-operation, the smaller servers see a pronounced increase in their extra load. The numbers suggest that it makes sense to do asymmetric co-operation, if extra load were the consideration.
We develop a simple metric to make such an evaluation. We define ri(p) as the relative increase in hit rate as seen by proxy server p due to co-operation in comparison to the extra number of requests it serves, i.e.,
![]()
The dependence of ri(p) on the set of co-operating proxies is implicit. Notice that, by definition, wc – nc excludes requests made directly to proxy p, and ri(p) can, therefore, be greater than 1.
A large value for ri(p) suggests that proxy p is involved in a "good" co-operation from its point of view. Various metrics can be defined to put together individual ri(p)'s to obtain a system-wide measure of fairness (e.g., a product function). We do not tackle system-wide fairness in this paper. Intuitively, a system-wide definition of fairness must include the relationship of the ri(p)'s to proxy p's hit rate without co-operation. Asymmetric co-operation implies that the smallest proxy in a co-operating set will have its ri value equal to infinity, and the largest proxy will have its ri value equal to 0.
Using the ri metric, Table 6 shows how useful it is for a server to co-operate.
|
|
||||||||||||||||||||||||||||||||||||||||||||||
We observe that with symmetric co-operation, the ri's are uniformly low for all servers. Not surprisingly, since the larger proxies serve more requests and encounter more faults (in absolute numbers), they can inundate a smaller proxy. (This can also be inferred from the data in Table 5 on extra load on a server.) They, therefore, end up having larger values of ri. With an asymmetric co-operation, there is no issue of fairness.
The second observation is based on putting together the hit rate improvement information with the results on extra intranet traffic and load on the server. If the proxies are of different "sizes" (meaning, serving different number of hosts), an asymmetric protocol would be preferable to a symmetric protocol. At the very least, the larger proxies should be more choosy in redirecting their misses to other proxies. Proxies should also have policies on rejecting or ignoring requests from other proxies based on their monitoring of how useful they are in serving the other proxy's requests.
The third observation is that it might be difficult to expect co-operation to be fair. We have observed that an asymmetric protocol is inherently not fair (in the sense that we have defined fairness in this paper), and a symmetric protocol is not particularly good for our measure of fairness. We infer from the numbers in this paper, and intuitively, that when the proxies are not all equal, a symmetric protocol has more chances of dragging everybody down.
The last observation is that even if co-operation can be implemented so that the response is fast, indiscriminate co-operation is not a good idea. Many a time, most of the benefit is obtained by co-operation with only one of many servers, and without care, the performance of the other servers will degrade unnecessarily.
Cache Management. One contribution of this work relates to what metrics proxies (or proxy managers) should employ to keep track of their performance, with respect to adapting co-operation policies. Based on this study, our opinion is that post-processing logs to configure proxy caches is inadequate. While proxy managers can use offline analyses and results of studies like rate of change metrics [2] to set caching policies, online monitoring and management must be provided for effective use of proxies and their features. Our ongoing work on building the PROXYMAN proxy caching manager uses some of the intuitions provided by this study. For PROXYMAN, we have defined a management information base (MIB) for a proxy caching server keeping in mind what monitored variables will be needed by future applications to improve the hit rate of proxy caches. Our prototype builds a manager/agent with capability to provide performance enhancements with intelligent monitoring.
The increasing importance of caching on the Web is well known [10]. We expect that in the future, proxies will have to be more adaptively configurable, incorporate new features (e.g., applet caching, host advertising services, etc.), and use techniques to reduce the cost of misses (by using delta encoding principles, for example [5]). Hit rate improvements directly impact network infrastructure costs and can be used for pricing the value of caching.
 |
P. Krishnan (who is called "Krishnan" or "PK") is a Member of Technical Staff at Bell Labs, Lucent Technologies. His research interests include IP management, the development and analysis of algorithms, prefetching and caching, and mobile computing. He received his Ph.D. in Computer Science from Brown University, and his B. Tech in Computer Science from the Indian Institute of Technology, Delhi. He can be reached at pk@research.bell-labs.com. |
 |
Binay Sugla is currently Department Head, Network and Services Management Research Department at Bell Labs, Lucent Technologies. Presently, he is working on tools and techniques for IP management. His past work produced tools like the Network Flight Simulator, a real-time simulator for networks, and CAPER, a concurrent application programming environment. He can be reached at sugla@bell-labs.com. |