 Fifth International World Wide Web Conference
Fifth International World Wide Web ConferenceMay 6-10, 1996, Paris, France
 Fifth International World Wide Web Conference
Fifth International World Wide Web Conference
Jean-Chrysostome Bolot (1) Philipp Hoschka (2)
INRIA
B. P. 93
06902 Sophia-Antipolis Cedex
France
{bolot,hoschka}@sophia.inria.fr
Our contribution is twofold. Regarding dimensioning, we advocate the use of time series analysis techniques for Web traffic modeling and forecasting. We show using experimental data that quantities of interest such as the number of Web requests handled by a server, or the amount of data retrieved per hour by a server, can be accurately modeled with time series such as seasonal ARIMA models. We then use these models to make medium-term predictions of client requests characteristics (number of such requests and size of document retrieved), which in turn can be used as a basis for dimensioning decisions. Regarding caching, we advocate the use of novel cache replacement algorithms that explicitly take document size and network load into account so as to minimize the retrieval time perceived by clients.
The World Wide Web provides a service of access to vast amounts of geographically distributed information. Clearly, the quality of the service depends on the quality of the access to the data. This quality in turn depends on a number of parameters, some of which are difficult to quantify. However, it appears that Web users rate access time to remote data as an essential component of quality. Thus, they tend to avoid overloaded servers and pages that take a long time to retrieve.
Access time to remote data (which we refer to in the paper as retrieval time, or Web latency) is made up of many components, which include i) the time for the client request to reach the server, ii) the time at the server to process the data, iii) the time for the reply to reach the client from the server, and iv) the time at the client to process the reply. Times i) and iv) depend on the hardware configurations at the client and at the server, on the type of client request, and on the load at the server. To avoid long delays, it is important to have enough client and server resources (CPU, disk size and disk access time, and memory size) to support the anticipated load. Times ii) and iii) together add up to what is referred to as the roundtrip delay between client and server. This delay is the sum of the delays experienced at each intermediate router between client and server. Each such delay in turn consists of two components, a fixed component which includes the transmission delay at a router and the propagation delay on the link to the next router, and a variable component which includes the processing and queueing delays at the router (Note that packets may be rejected at the intermediate nodes because of buffer overflow, causing packet loss). To avoid large roundtrip delays, it is important to have enough network resources (bandwidth and buffer sizes at the routers) to support the anticipated load, and to control the amount of data that is sent into the network. This latter control can be done in many different ways, one of which being to minimize the number of client requests sent to distant servers, which is typically done with caching.
Thus, it is clear that the quality of the service provided by the Web depends on the careful match of network and server resources to anticipated demand, and on the careful design of caching schemes. The art of matching resources to anticipated demand is referred to as resource/capacity planning, or dimensioning. We use the term dimnesioning in the paper. Thus, dimensioning and cache design are the focus of this paper.
In Section 2, we consider issues related to dimensioning. Specifically, we use time series analysis to model the number of client requests arriving at a Web server and the amount of data sent by a Web server back to its clients. We show using experimental trace data that the above quantities can be accurately modeled with so-called seasonal autoregressive integrated moving average (seasonal ARIMA) models. These models are then used to make short and medium term predictions of client requests characteristics (number of such request and size of document retrieved), which in turn can be used as a basis for dimensioning decisions. ARIMA models have been used in many different areas to make reasonable medium- and sometimes even long-term predictions. Thus, they hold great promise as a tool for Web traffic forecasting and hence for Web server dimensioning.
In Section 3, we consider issues related to cache design, in particular proxy cache design. A client request for a document that is not present in the cache may require that one or more cached documents be replaced by the requested (and newly fetched) document. Which documents are replaced is determined by a so-called cache replacement algorithm. Most recently proposed such algorithms use the frequency of reference, and sometimes the size, of the documents requested by clients to replace documents. Surprisingly, they do not explicitly take retrieval time into account, even though their goal is precisely to minimize, or at least to reduce, the retrieval time perceived by clients. We introduce a very general class of cache algorithms that do take retrieval time and other relevant parameters into account. We show using using experimental data collected at INRIA that these algorithms outperform commonly used algorithms.
Section 4 concludes the paper.
Measurements at a connection endpoint such as a Web client/server site in the Internet can be obtained in a passive or active fashion. Passive measurements typically involve collecting request and/or reply information at client or server sites. Active measurements typically involve collecting information such as delay and loss distribution about the connection between client and server.
With the passive method, we obtain measures such as the number of requests reqn to a Web server during the nth measurement interval. With the active method, we obtain measures such as the roundtrip delay rttn of packet n . If packet n is a HTML client request, then rttn measures the retrieval time associated with this request. Trace data obtained with the passive method is shown later in Figures 2 and 3. Trace data obtained with the active method is shown in Figure 1. Figure 1 shows the evolutions of rttn as a function of n in the range 0 <= n <= 15000 obtained from a trace collected at Boston University [5].
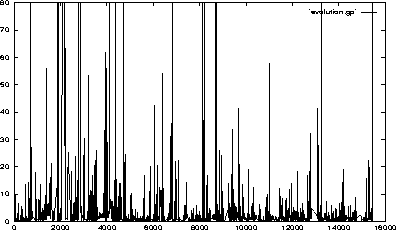
Figure 1: Evolution of rttn (in seconds) vs. n
The evolutions of rttn in Figure 1 are an example of a time series plot, by which is meant a finite set of observations of a random process in which the parameter is time. A large body of principles and techniques referred to as time series analysis has been developed to analyze time series, the goal being to infer as much as possible about the whole process from the observations [11]. It is thus natural to investigate whether and how well these techniques can be applied to Web data. The most important problems in time series analysis are the model fitting problem and the prediction problem. In the first problem, the goal is to obtain a statistical model which fits the observations. In the second problem, the goal is to predict a future value of a process given a record of past observations. We describe the model fitting problem next.
Constructing a time series model involves expressing rttn in terms of previous observations rttn-i , and of noise processes en which typically represent external events. The noise processes are generally assumed to be uncorrelated white noise processes with zero mean and finite variance. These are the simplest processes, and they correspond to processes that have ``no memory'' in the sense that the value of a noise process at time n is uncorrelated with all past values up to time n-1. Thus, for n>0, we express rttn as follows
rttn = f({rttn-i}, {en-i}, i>=0)
We now need to take a closer look at how to define the function f. Most models described in the literature are linear models, the most well-known being the so-called AR (autoregressive), MA (moving average), and ARMA (auto regressive and moving average) models. An autoregressive model of order p (denoted by AR(p) ) describes the current value rttn using the weighted sum of p previous values rttn-1, ..., rttn-p, plus one noise term en. A moving average of order q (denoted by MA(q) ) describes the current value rttn using the weighted sum of q noise terms. An ARMA model of order (p,q) combines the above models and describes the current value rttn using p previous values of rtt and q noise terms. Specifically
(1) rttn = x1rttn-1+ ... + xprttn-p - y0en - y1rttn-1 - 1 - ... - ypen-p
where x1 ... xp and y1 ... yq are constant values.
This equation is typically rewritten as
(2) X(B)rttn = Y(B)en
where B is a lag operator defined as Brttn = rttn-1 , and X and Y are polynomial operators defined as X(B) = 1 - x1B - x2B**2 - ... - xpB**p and Y(B) = -y0 - y1B - y2B**2 - ... - yqB**q. In these equations and for the rest of this paper, A**B stands for "A to the power of B".
ARMA models have been widely used to analyze time series in many different areas. For example, they have been used to describe video traffic, call requests in telephone networks [8], and memory references in software [9]. However, they have been comparatively rarely applied in computer networking.
Fitting an ARMA model to time series data is done in three steps, which are i) identification (i.e. determine the values of p and q in equation 1), ii) estimation (i.e. estimate the constants x1 ... xp, y1 ... yq) , and iii) evaluation or diagnostic checking (i.e. check how well the fitted model conforms to the data, and suggest how the model should be changed in case of a lack of good fit). Once a good model has been obtained with this method, it can be used for example to make forecasts (predictions) of the future behavior of the system.
The ARMA model fitting procedure assumes the data to be stationary. Specific approaches have been developed if the time series shows variations that violate this stationarity assumption. The more commonly used approach is to use two models, one for the non stationary part of the process, the other for the ``residual'' part which remains after the non stationary effects have been removed. If the non stationary part is a polynomial function of time, then the overall process can be modeled with integrated models such as the ARIMA model. An ARIMA model of order (p, d, q) is an ARMA (p, q) model that has been differenced d times. Thus it has the form
(3) ((1 - B)**d)X(B)rttn = Y(B)en
where X(B) and Y(B) are the same as in equation 2.
Unfortunately, many ``real-life'' time series include non-polynomial non-stationarities that cannot be removed simply by differencing. The most common such non-stationarities are seasonal trends. For example, the data for a particular hour in a month-long trace is typically correlated with the hours preceeding it as well as to the same hours in preceeding days. Seasonal trends can be taken into account in seasonal ARIMA models, which are referred to as ARIMA (p,d,q) × (P,D,Q)s models. The idea in these models is to carry out two separate ARMA analyses, one for the entire series, and another one only for data points that are s units apart in the series. In practice, the original series is first differenced by the length of the period s . The resulting series is analyzed according to order (P,D,Q) while the original series is analyzed to order (p,d,q).
We have used the techniques above to analyze trace data collected at one of INRIA's Web servers. The data includes the number of requests handled by the server and the size (i.e. the number of bytes) of the corresponding replies. The data has been collected between December 1, 1994 and July 31, 1995. We are interested in the hourly variations of the data. To simplify data analysis, we consider averages over a period of one month. Figure 2 shows the average number of requests (computed over a month) received every hour. The hours are numbered 0 to 23, with 0 corresponding to midnight. Thus, the first data point in the figure represents the average number of requests received during November 1994 between midnight and 1:00 am. The second data point represents the average number of requests received during between 1:00 and 2:00 am, etc. Thus, Figure 2 can be thought of as showing the evolutions of the number of requests in a typical day in November, December, etc.
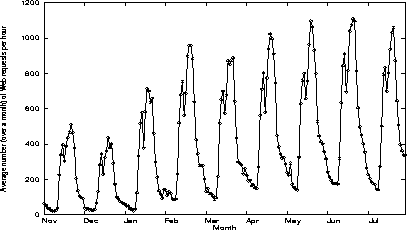
Figure 2: Evolutions of the average number (over a month) of Web requests per hour
As expected, we observe strong seasonal variations which correspond to daily cycles. The number of Web requests is smallest at night between 8:00 pm and 6:00 am. We also observe a slight dip around noontime. This strong daily cycle suggests that most requests to this server originate in France, or at least in countries with little time difference with France. Indeed, more than 60%of the requests originate in the .fr, .uk, and .de domains (corresponding to France, the UK, and Germany, respectively), while requests originating in the .edu, .gov, .mil, and .jp domains account for less than 15% of the total.
In addition to daily cycles, we observe a trend which reflects the growing number of requests handled by the server over the past year. We have used differencing to remove the trend. Although most of the non-stationarity is removed by the first differencing, we observe an additional effect when differencing is done twice. Thus, we tentatively set d = 2. Clearly, the seasonal period is s = 24. Model identification then proceeds using standard identification techniques [11] implemented in Matlab (Matlab is a trademark of The MathWorks, Inc.). We have found that the seasonal ARIMA model (2,2,1) × (3,2,0)24 provides a good fit to the data.
We have carried out a similar identification procedure for the number of Mbytes requested from the server.
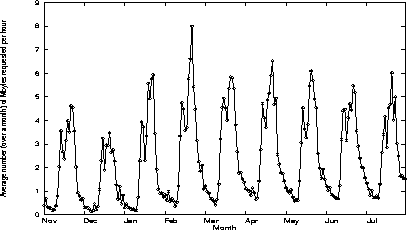
Figure 3: Evolutions of the average number (over a month) of bytes sent by the server per hour
Figure 3 shows the average number of bytes (computed over a month) sent every hour by the server. Not surprisingly, we observe the same strong daily cycles as in Figure 2. However, the overall trend which reflects the growing number of bytes transfered is not as clear as that found above.
We have used the seasonal models developed above for forecasting purposes. Forecasting the number of requests is useful to dimension and plan upgrades to the server. Forecasting the number of bytes transfered is useful to dimension the networks over which these bytes are transfered (in our specific case, these include INRIA's own network as well as the regional network for southeastern France). The forecasting problem may be posed as follows: Given a series of values observed up to time n (such as the number of requests {reqn}), predict the value of req at some specific time in the future, say reqn+k, that minimizes some prediction error, which we take here to be the mean square prediction error. With an ARIMA(p,d,q) model such as that of equation 3 and its seasonal extension, the minimum square error forecast for reqn+k, which we denote by reqn+k~ , is given by [11]
(4) reqn+k~ = sum(i=1,p) xi reqn+k-i~ - sum(j=1,q) xi yj 0en+k-j
where 0en+j = en+j if j <= 0 and 0en+j = 0 otherwise. Note that we assume above that the parameters xi, yi,, p, and q of the ARIMA model are known. In practice, they are of course estimated from trace data as shown earlier.
We have found that ARIMA-based forecasting does provide reasonably accurate short- and medium-term predictions. Table 1 shows the predicted and actual values of the average number of Web requests per hour for the month of October 1995. We have used the above ARIMA predictor to forecast the number of requests from the trace data shown in Figure 2 (i.e. using data from November 1994 to July 1995).
| Hour | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Actual | 316 | 282 | 278 | 264 | 209 | 210 | 170 | 201 | 441 | 913 | 1193 | 1271 |
| Predicted | 320 | 275 | 250 | 245 | 200 | 202 | 185 | 185 | 295 | 680 | 870 | 980 |
| Hour | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| Actual | 1043 | 1320 | 1439 | 1577 | 1609 | 1420 | 1096 | 689 | 550 | 470 | 495 | 426 |
| Predicted | 740 | 910 | 1130 | 1320 | 1300 | 1105 | 920 | 550 | 510 | 430 | 380 | 360 |
Table 1: Actual and predicted values of requests for the month of November
We observe that the predicted values do reflect the daily variations observed in the data. However, they are in general lower than the actual values by 10 to 30%. Our ability to make reasonable medium- and long-term forecasts is limited at present because the amount of trace data available is quite limited. In particular, we do not have enough data for the ARIMA model to capture the long term growth data of Web traffic, and to capture yearly cycles. Yet both factors obviously have an important impact. For example, Figure 2 clearly shows dips for the months of December and July that reflect decreased activity caused by Christmas and summer vacations.
Measurements have shown that proxy caching can significantly reduce network load [1]. This is because a proxy server returns the locally cached copy of a document named in a URL from a previous client request if this document is requested again. However, proxy caching decreases the network load as well as the retrieval time perceived by the client only if client requests exhibit a sufficiently high degree of what is referred to in the literature as temporal locality. ``Temporal locality'' is a bit of a misnomer, and temporal proximity (as suggested by a reviewer) would be more appropriate. Temporal locality implies that identical requests (possibly from different clients) follow each other closely in time with high probability. The property of temporal locality has been observed in many situations, including program execution [10], file and database access [14], and network addresses in data packets [6][7].
A hit is said to occur in the cache when a document named in a URL from a previous request is already in the cache. A fault or miss is said to occur when the document is not found in the cache. On a cache miss, one of the entries in the cache must be replaced to bring in the missing document. Several replacement algorithms have been described in the literature, the more notable of which as the Least Recently Used (LRU) algorithm and its many derivatives [1]. The LRU algorithm orders cache entries in a stack. On a cache miss, the LRU algorithm moves the missed name to the top of the stack and discards the entry at the bottom of the stack. The algorithm attempts to approximate an ``optimal'' algorithm, which would replace the entry that will be referenced farthest in the future. This algorithm requires to look ahead in the trace, and hence it cannot be implemented in a real system.
We compare the performance of replacement algorithms using two measures, namely the miss ratio and the normalized resolution time. The miss ratio or miss probability is defined as the probability that a requested document is not already in the cache. Clearly, the lower the miss ratio, the lower the network resource requirements of the client requests. However, the client is not so much interested in the miss ratio as in the decrease in perceived retrieval time made possible by the use of the cache. Thus, we quantify the performance improvements gained by using the cache via the normalized resolution time t, which is equal to the ratio of the average name resolution time with and without the cache. The lower t is, the higher the performance increase gained with proxy caching.
Let p denote the miss probability, Tc denote the average time to access an entry in the cache, and Tnc denote the average time to retrieve a document which is not in the cache. Then
(5) t = (Tc + pTnc)/Tnc
Assuming that Tnc is much bigger than Tc , t is about equal to p. Therefore, t is minimized if p is minimized.
This seems to argue for as large a cache as possible. However, the cache size is limited in practice. Furthermore, the miss ratio is in general a function of the size of the documents in the cache. Indeed, for a given cache size, the number of cached documents and hence the hit ratio decrease with the average document size. Also, experimental evidence suggests that smaller documents are more often requested by clients [5]. This has led to the introduction of cache replacement algorithms that do not depend on temporal locality only, but on document size as well [1].
Surprisingly, however, no Web cache algorithm we are aware of takes as input parameter the time it took to retrieve a remote document (and insert it in the cache). Yet it seems natural that a decision to discard from the cache a document retrieved from a far out (in terms of network latency) site should be taken with greater care than the decision to discard a document retrieved from a closer site, all the more so since the time required to retrieve documents from different sites can be considerably different one from the other as illustrated in Figure 1. Thus, we argue that Web cache replacement algorithms should take into account the retrieval time associated with each document in the cache. One way to do this is to assign a weight to each item in the cache, and to use a weight-based replacement algorithm which replaces the item with the lowest current weight in the cache (this is a generalization of the frequency-based algorithm described in [12]. In general, the weight could be a function of the time to last reference of the item, the time it took to retrieve the item, the expected time-to-live of the item, the size of the document, etc. Such weight-based algorithms have been advocated for distributed database systems [13].
In general, the problem of selecting an algorithm for replacing documents in a cache is a function that, given a state s for the cache (defined below), and a newly retrieved document i, decides i) if document i should be cached, and ii) in case answer to question i) is positive but there is not enough free space in the cache to include the document, which other document(s) should be discarded to free the space needed. We define the state of the cache to be i) the set of documents stored in the cache and ii) for each document a set of state variables which typically include statistical information associated with the document. Examples of state variables associated with document i include
We assign a weight to each cached document i that is a function of the state variables associated with document i. We denote the weight function by Wi = W(ti, Si, rtti, ttli). Observe that this general weight function can be specialized to yield commonly used algorithms. For example, with the function W(ti, Si, rtti, ttli) = 1/ti, documents are replaced according to the time of last reference. This models the LRU algorithm. With W(ti, Si, rtt i, ttl i) = Si, documents are cached on the basis of size only. The general form of the weight function depends on the application, and more specifically on the types of requests and replies expected in the system. For Web proxy caching, we suggest the following function
(6) W(ti, Si, rtti, ttli) = (w1rtti+w2 Si)/ttli + (w3 +w4)/ti
where w1, w2, w3 and w4 have constant value. The second term on the right-hand side captures the temporal locality. The first term captures the cost associated with retrieving documents (waiting cost, storage cost in the cache), while the multiplying factor 1/ttli indicates that the cost associated with retrieving a document increases as the useful lifetime of the document decreases.
It is not clear yet how to best handle the cache coherence problem in the Web. Recent work suggests that hierarchical invalidation schemes are not as attractive as might have been expected. Instead, remote sites exporting time-critical documents should associate adequate expiration times (i.e. ttl values) to these documents [3][2]. Our model above is geared towards such schemes. However, few sites already implement these schemes. Thus, it is difficult in practice to obtain a value for the state variable ttli. Therefore, we do not consider it in the rest of the paper. In this case, Equation 6 becomes
W(ti, Si, rtti, ttli) = w1rtti+w2 Si+(w3+w4 Si)/ti
There remains to define parameters wi. Not surprisingly, the choice of adequate values for wi depends on the goal of the caching algorithm. This goal might be to maximize the hit ratio, or to minimize the perceived retrieval time for a random user, or to minimize the cache size for a given hit ratio, etc. Each goal can be expressed as a standard optimization problem, and solved using variants of the Lagrange multiplier technique. We do not describe these optimization problems here (to save space and because they do not add much insight into the design of the algorithms). Instead, we use trace-driven simulation to compare the performance of various schemes. A trace-driven simulation requires a trace of requests sent to remote servers and a model of the cache being simulated. The cache model can be altered to simulate a cache of any size with any type of replacement algorithm, and the simulation can be repeated on the same trace data.
We consider 2 different cache replacement algorithms, namely the LRU algorithm and an algorithm that takes all state variables into account. We refer to these algorithms as algorithm 1 and 2, respectively. They are defined as follows
The performance measures we consider are the miss ratio, and a weighted miss ratio defined as the probability that a requested document is not already in the cache multiplied by the weight associated with that document. In the same way, we define a weighted miss history which records the number of misses, multiplied by the weight associated with a miss, versus the number of documents that have been processed by the simulator. Figure 4 shows the weighted miss history for both algorithms.
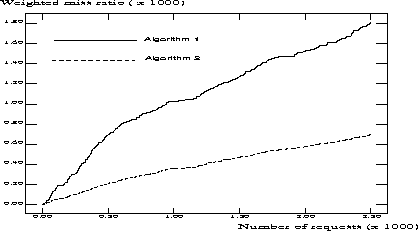
Figure 4: Weighted miss histories for algorithms 1 and 2
It turns out that the miss ratio for algorithm 1 is slightly lower than that for algorithm 2. However, the weighted miss ratio, and hence the perceived retrieval time, is much lower for algorithm 2. This clearly shows the benefits of using cache replacement algorithms that take retrieval time into account.
Our contributions in the paper can be summarized as i) it is reasonable to use time series analysis techniques to model Web traffic and forecast Web server load, and ii) cache replacement algorithms should be a function of variables other than simply time to last reference and document size. The results we have presented to support these claims are preliminary. However, they are very encouraging. We are now working on precisely quantifying the gains associated with the techniques we have advocated here.
Many thanks to the anonymous reviewers for carefully reading the paper, and for useful comments.