BuzzRank ...and the Trend is Your Friend

Klaus Berberich

Max-Planck-Institut für Informatik
Saarbrücken, Germany

Srikanta Bedathur

Max-Planck-Institut für Informatik
Saarbrücken, Germany

Michalis Vazirgiannis

Athens University of Economics and Business
Athens, Greece

Gerhard Weikum

Max-Planck-Institut für Informatik
Saarbrücken, Germany

Copyright is held by the author/owner(s).
WWW 2006, May 23.26, 2006, Edinburgh, Scotland.
ACM 1-59593-323-9/06/0005.

ABSTRACT

Ranking methods like PageRank assess the importance of Web pages based on the current state of the rapidly evolving Web graph. The dynamics of the resulting importance scores, however, have not been considered yet, although they provide the key to an understanding of the Zeitgeist on the Web. This paper proposes the BuzzRank method that quantifies trends in time series of importance scores and is based on a relevant growth model of importance scores. We experimentally demonstrate the usefulness of BuzzRank on a bibliographic dataset.

Categories & Subject Descriptors

H.4.m [Information Systems]: Miscellaneous

General Terms

Algorithms, Measurement

Keywords

Web graph, Web dynamics, PageRank


1 Motivation

Link-based ranking methods like PageRank [7] play a crucial role in today's search engines. In this context, such methods indicate the importance of individual Web pages based on the current state of the Web graph. This current state contains all pages and links that were added but not yet removed and is thus the result of the Web's entire evolution. However, methods like PageRank do not properly reflect the evolutionary trajectory of the Web (i.e., links and pages recently removed or added), which is substantial as reported in [2,5,6]. As a consequence, PageRank and the like are not appropriate to serve information needs on timelines and trends as the following example demonstrates.

We use a bibliographic network derived from the Digital Bibliography & Library Project (http://dblp.uni-trier.de) as a showcase here, since obtaining an adequate Web dataset would involve frequent crawling of a significant fraction of the Web. Let us, on the one hand, consider an information need for seminal publications in database research. In our bibliographic network, PageRank identifies E. F. Codd's A Relational Model of Data for Large Shared Data Banks as the most important publication, which is reasonable given this information need. On the other hand, the information need could be for publications in databases that are not yet very important but currently gain a lot of importance; a scenario for which PageRank fails as the example demonstrates. Figure 1 plots PageRank scores of the aforementioned publication and Agrawal et al.'s Mining Association Rules between Sets of Items in Large Databases for the years 1990 through 1999. Although, for any of the depicted times Codd's paper is ahead in terms of importance by an order of magnitude at least, its importance score is close to stagnation. In contrast, the other paper improves its importance score in the considered period by a factor of more than ten.

Figure 1: Time-series of PageRank scores
\begin{figure}\centering %\includegraphics[width=0.4\columnwidth, angle=-90]{pdf/pagerank-over-time.pdf}\ \vspace{-2.5mm} \vspace{-0.55cm} \end{figure}
If the second information need arises at any point between 1993 and 1999, Agrawal et al.'s paper could be identified as a better result by means of the trend contained in its time series of PageRank scores.

The BuzzRank method proposed in this work builds on this idea. It analyzes time series of importance scores and quantifies the contained trends based on a growth model of importance scores. Thus, for instance, in a bibliographic network, the method identifies those publications that have significantly increased their importance in a specific time interval, which -more colloquially- are the publications that caused significant buzz in that period. Therefore, BuzzRank's objectives differ from earlier related work [1,3,8] that sought to improve link-based importance ranking by means of temporal features. However, BuzzRank is complementary rather than a replacement to PageRank, and thus seeks to serve information needs as the one above.



2 BuzzRank

BuzzRank exploits the fact that importance scores co-evolve with the Web graph and considers the following time series of importance scores for individual pages.

Let $G_t(V_t,E_t)$ denote the graph snapshot at time $t$ consisting of the set of nodes $V_t$ and the set of edges $E_t$. The vector of PageRank scores computed on the graph $G_t$ is referred to as $r_t$. Since PageRank scores are not comparable across graphs from different points in time (with different graph sizes), a new kind of normalization problem arises that we solve as follows. The vector $r_t$ is normalized dividing by

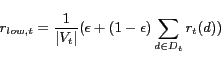
\begin{displaymath}r_{low, t} = \frac{1}{\vert V_t\vert} (\epsilon + (1-\epsilon) \sum_{d\in D_t}r_t(d))\end{displaymath}

with the damping factor $\epsilon$ and $D_t$ as the set of dangling nodes (i.e., nodes without outgoing edges) at time $t$. The value $r_{low, t}$ is the lower bound for the PageRank score assigned to a node without incoming edges.

For an individual node $v$ we consider the time series of importance scores

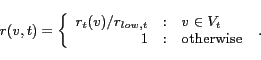
\begin{displaymath}r(v,t) = \left\{ \begin{array}{r@{\quad :\quad}l} r_t(v) / r... ... & v\in V_t \ 1 & \mbox{otherwise} \end{array}\right. \;. \end{displaymath}

Thus, if a node is not present at time $t$, the time series assumes $1$, i.e., treats the node as if it was present but had no incoming edges. The time series shown in Figure 1 were obtained using this definition. The BuzzRank method quantifies trends in the time series for observations in a time-interval $[t_{begin},t_{end}]$, which is an input parameter to the method. For the time series, we assume that observations are available for a series of timestamps $\langle t_0,\ldots,t_n\rangle \subset [t_{begin},t_{end}]$. In a Web search engine, as an example, these could be the times when PageRank scores were updated.

The growth of PageRank scores over time has been modeled by Cho et al. [4] using the logistic growth model (aka. Verhulst growth model) - a specific case of the following generic growth model:

\begin{displaymath}\hat{r}(v,t) = e^{\:\int_0^t\alpha_v(t) dt}\;\end{displaymath}

In this model the parameter $\alpha_v(t)$ gives the growth rate of the node's PageRank score at time $t$.

We assume for the growth rate $\alpha_v(t)$ that it is time-invariant as $\alpha_v$ within $[t_{begin},t_{end}]$. Later this assumption is empirically substantiated. Using the time-invariant growth rate we obtain the following exponential growth model for times in the considered time interval

\begin{displaymath}\hat{r}(v,t) = r(v,t_{begin}) \: e^{\,\alpha_v\,(t - t_{begin})}\quad\mbox{:}\quad t_{begin}\le\,t\,\le t_{end}\;.\end{displaymath}

Since the series of observation times $\langle t_0,\ldots,t_n\rangle$ does not necessarily include $t_{begin}$, the value $r(v,t_{begin})$ may be unknown. Therefore, an additional parameter $A_{v,t_{begin}}$ is introduced to the model, so that we obtain the final model

\begin{displaymath}\hat{r}(v,t) = A_{v,t_{begin}} \: e^{\,\alpha_v\,(t - t_{begin})}\quad\mbox{:}\quad t_{begin}\le\,t\,\le t_{end}\;.\end{displaymath}

Using the method of least squares we fit the model to the observed time series values, i.e., we minimize

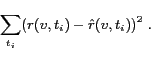
\begin{displaymath}\sum_{t_i} (r(v,t_i) - \hat{r}(v,t_i))^2\;.\end{displaymath}

Applying a log-transformation to both $r(v,t_i)$ and $\hat{r}(v,t_i)$ the problem is reduced to fitting a straight line. The optimal parameter value $A_{v,t_{begin}}^*$, on the one hand, estimates the node's PageRank score at time $t_{begin}$ and is not considered further. The optimal parameter value $\alpha_v^*$, on the other hand, estimates the growth rate of the node's PageRank score in the considered time interval.

This growth rate $\alpha_v^*$ quantifies the trend in the time series of the node's importance scores and thus, as we argued in the introduction, is a good indicator for the buzz caused by the node in the considered time-interval. BuzzRank provides its final ranking assigning every node $v$ its estimated growth rate $\alpha_v^*$ as a score.



3 Experiments

Since no adequate Web dataset is available (i.e., time series of periodically repeated Web crawls), we use the free DBLP bibliographic dataset for our preliminary experiments. We only consider the period from 1989 through 1999 as this period has the most densely recorded citations in DBLP. In the graph that we derive from DBLP nodes represent publications and edges represent citations.

As input to BuzzRank we computed PageRank vectors for the graphs at times corresponding to the begins of the years 1989 through 1999 yielding a total of eleven observations per time series. The damping factor for the PageRank computations was set to $\epsilon = 0.15$.

In the first of our experiments, we empirically analyze our assumption that $\alpha_v(t)$ can be considered as time-invariant. Note that if $\alpha_v(t)$ is nearly constant over a period of $k$ successive observations, there must be a strong linear relationship observable between $\langle t_i,\ldots,t_{i+k}\rangle$ and the log-transformed time series values $\langle log\,r(v,t_i),\ldots,log\,r(v,t_{i+k})\rangle$. Therefore, we computed correlation coefficients for varying $k$ across all nodes. Since we are only interested in the strength of the linear relationship but not in its direction, we computed average absolute correlation coefficients for different values of $k$. For three successive observations (i.e., $k=2$) this yields a value of $0.91$. For four up to seven successive observations, slightly lower but consistent values about $0.85$ are observed. Thus, there is a strong linear relationship and therefore assuming time-invariance for $\alpha_v(t)$ is reasonable.

As a second experiment we computed rankings using BuzzRank for two year intervals (i.e., three successive observations). For most publications in DBLP only the year of publication is known, consequently granularities more fine-grained than the year-level are not meaningful. In Table 1 the publications top-ranked by BuzzRank for the two year intervals are given.

Table 1: Publications top-ranked by BuzzRank
Years Title
['89, '90] The Object-Oriented Database System Manifesto
['90, '91] CYC: Toward Programs With Common Sense
['91, '92] ARIES: A Transaction Recovery Method Supporting Fine-Granularity Locking and Partial Rollbacks Using Write-Ahead Logging
['92, '93] Simplifying Decision Trees
['93, '94] World-Wide Web: The Information Universe
['94, '95] The Power of Languages for the Manipulation of Complex Values
['95, '96] Towards Heterogeneous Multimedia Information Systems: The Garlic Approach
['96, '97] Implementing Data Cubes Efficiently
['97, '98] Modeling Multidimensional Databases
['98, '99] XML-QL: A Query Language for XML

The results indicate that BuzzRank indeed brings publications related to hot topics in the respective period to the top. For the intervals $[1993,1994]$ and $[1998,1999]$, for instance, publications related to the Web and XML are ranked at the top respectively. In marked contrast, the use of PageRank resulted in the publication by E. F. Codd mentioned in the Motivation to be the top-ranked item in each time interval.

REFERENCES

[1] E. Amitay, D. Carmel, et al.
Trend Detection Through Temporal Link Analysis.
JASIST, 55(14):1270-1281, 2004.

[2] Z. Bar-Yossef, A. Z. Broder, et al.
Sic Transit Gloria Telae: Towards an Understanding of the Web's Decay.
WWW '04.

[3] K. Berberich, M. Vazirgiannis, et al.
Time-aware Authority Ranking.
Internet Mathematics, 2006.

[4] J. Cho, S. Roy, et al.
Page Quality: in Search of an Unbiased Web Ranking.
SIGMOD '05.

[5] D. Fetterly, M. Manasse, et al.
A large-scale study of the evolution of web pages.
Software: Practice and Experience, 34(2):213-237, 2004.

[6] A. Ntoulas, J. Cho, et al.
What's New on the Web?: The Evolution of the Web from a Search Engine Perspective.
WWW '04.

[7] L. Page, S. Brin, et al.
The PageRank Citation Ranking: Bringing Order to the Web.
Stanford Tech. rep., 1998.

[8] P. S. Yu, X. Li, et al.
On the Temporal Dimension of Search.
WWW '04.