A Web-based Kernel Function for Measuring the Similarity of Short Text Snippets
1 Introduction
In analyzing text, there are many situations
in which we wish to determine how similar two short text snippets
are. For example, there may be different ways to describe some
concept or individual, such as ``United Nations
Secretary-General'' and ``Kofi Annan'', and we would like to
determine that there is a high degree of semantic
similarity between these two text snippets. Similarly, the
snippets ``AI'' and ``Artificial Intelligence'' are very similar
with regard to their meaning, even though they may not share any
actual terms in common. Directly applying traditional document
similarity measures, such as the widely used cosine coefficient
[17,16], to such short text
snippets often produces inadequate results, however. Indeed, in
both the examples given previously, applying the cosine would
yield a similarity of 0 since each given text pair contains no
common terms. Even in cases where two snippets may share terms,
they may be using the term in different contexts. Consider the
snippets ``graphical models'' and ``graphical interface''. The
first uses graphical in reference to graph structures
whereas the second uses the term to refer to graphic displays.
Thus, while the cosine score between these two snippets would be
0.5 due to the shared lexical term ``graphical'', at a semantic
level the use of this shared term is not truly an indication of
similarity between the snippets. To address this problem, we
would like to have a method for measuring the similarity between
such short text snippets that captures more of the semantic
context of the snippets rather than simply measuring their
term-wise similarity. To help us achieve this goal, we can
leverage the large volume of documents on the web to determine
greater context for a short text snippet. By examining documents
that contain the text snippet terms we can discover other
contextual terms that help to provide a greater context for the
original snippet and potentially resolve ambiguity in the use of
terms with multiple meanings. Our approach to this problem is
relatively simple, but surprisingly quite powerful. We simply
treat each snippet as a query to a web search engine in order to
find a number of documents that contain the terms in the original
snippets. We then use these returned documents to create a
context vector for the original snippet, where such a
context vector contains many words that tend to occur in context
with the original snippet (i.e., query) terms. Such context
vectors can now be much more robustly compared with a measure
such as the cosine to determine the similarity between the
original text snippets. Furthermore, since the cosine is a valid
kernel, using this function in conjunction with the generated
context vectors makes this similarity function applicable in any
kernel-based machine learning algorithm [4] where (short) text
data is being processed. While there are many cases where getting
a robust measure of similarity between short texts is important,
one particularly useful application in the context of search is
to suggest related queries to a user. In such an application, a
user who issues a query to a search engine may find it helpful to
be provided with a list of semantically related queries that he
or she may consider to further explore the related information
space. By employing our short text similarity kernel, we could
match the user's initial query against a large repository of
existing user queries to determine other similar queries to
suggest to the user. Thus, the results of the similarity function
can be directly employed in an end-user application. The approach
we take in constructing our similarity function has relations to
previous work in both the Information Retrieval and Machine
Learning communities. We explore these relations and put our work
in the context of previous research in Section 2. We then formally define
our similarity function in Section 3 and present initial examples of
its use in Section 4. This is followed by a
mathematical analysis of the similarity function in Section
5. Section
6 presents a
system for related query suggestion using our similarity
function, and an empirical evaluation of this system is given in
Section 7.
Finally, in Section 8
we provide some conclusions and directions for future work.
2 Related Work
The similarity function we present here is
based on query expansion techniques [3,13] which have long
been used in the Information Retrieval community. Such methods
automatically augment a user query with additional terms based on
documents that are retrieved in response to the initial user
query or by using an available thesaurus. Our motivation for and
usage of query expansion greatly differs from this previous work,
however. First, the traditional goal of query expansion has been
to improve recall (potentially at the expense of precision) in a
retrieval task. Our focus, however, is on using such expansions
to provide a richer representation for a short text in order to
potentially compare it robustly with other short texts. Moreover,
traditional expansion is focused on creating a new query for
retrieval rather than doing pair-wise comparisons between short
texts. Thus, the approach we take is quite different than the use
of query expansion in a standard Information Retrieval context.
Alternatively, information retrieval researchers have previously
proposed other means of determining query similarity. One early
method proposed by Raghavan and Sever [14] attempts to
measure the relatedness of two queries by determining differences
in the ordering of documents retrieved in response to the two
queries. This method requires a total ordering (ranking) of
documents over the whole collection for each query. Thus,
comparing the pairwise differences in rankings requires
3 A New Similarity Function
Presently, we formalize our
kernel function for semantic similarity. Let 1. Issueas a query to a search engine
.
2. Letbe the set of (at most)
retrieved
documents
3. Compute the TFIDF term vectorfor each
document
4. Truncate each vectorto include its
highest
weighted terms
5. Letbe the centroid of the
normalized
vectors:
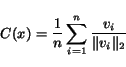
6. Letbe the
normalization of the centroid
:
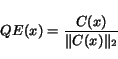 We note that to be precise, the computation of
We note that to be precise, the computation of 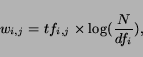
where
Observation 1  is a valid kernel function.
is a valid kernel function.
This readily follows from the fact that
4 Initial Results With Kernel
To get a cursory evaluation for
how well our semantic similarity kernel performs, we show results
with the kernel on a number of text pairs, using the Google
search engine as the underlying document retrieval mechanism. We
attempt to highlight both the strengths and potential weaknesses
of this kernel function.We examined several text snippet pairs to determine the similarity score given by our new web-based kernel, the traditional cosine measure, and the set overlap measure proposed by Fitzpatrick and Dent. We specifically look at three genres of text snippet matching: (i) acronyms, (ii) individuals and their positions, and (iii) multi-faceted terms.3 Examples of applying the kernel are shown in Table 1, which is segmented by the genre of matching examined. The first section of the table deals with the identification of acronyms. In this genre, we find two notable effects using our kernel. First, from the relatively high similarity scores found between acronyms and their full name, it appears that our kernel is generally effective at capturing the semantic similarity between an acronym and its full name. Note that the kernel scores are not 1.0 since acronyms can often have multiple meanings. Related to this point, our second observation is that our kernel function (being based on contextual text usage on the web) tends to prefer more common usages of an acronym in determining semantic similarity. For example, the text ``AI'' is determined to be much more similar to ``artificial intelligence'' than ``artificial insemination'' (even though it is a valid acronym for both), since contextual usage of ``AI'' on the web tends to favor the former meaning. We see a similar effect when comparing ``term frequency inverse document frequency'' to ``tf idf'' and ``tfidf''. While the former acronym tends to be more commonly used (especially since the sub-acronyms ``tf'' and ``idf'' are separated), the still reasonable score over 0.5 for the acronym ``tfidf'' shows that the kernel function is still able to determine a solid level of semantic similarity. It is not surprising that the use of cosine similarity is entirely inappropriate for such a task (since the full name of an acronym virtually never contains the acronym itself). Moreover, we find, as expected, that the set overlap measure leads to very low (and not very robust) similarity values. Next, we examined the use of our kernel in identifying different characterizations of individuals. Specifically, we considered determining the similarity of the name of a notable individual with his prominent role description. The results of these examples are shown in the second section of Table 1. In order to assess the strengths and weaknesses of the kernel function we intentionally applied the kernel to both correct pairs of descriptions and individuals as well looking at pairs involving an individual and a close, but incorrect, description. For example, while Kofi Annan and George W. Bush are both prominent world political figures, the kernel is effective at determining the correct role matches and assigning them appropriately high scores. In the realm of business figures, we find that the kernel is able to distinguish Steve Ballmer as the current CEO of Microsoft (and not Bill Gates). Bill Gates still gets a non-trivial semantic similarity with the role ``Microsoft CEO'' since he was indeed the former CEO, but he is much more strongly (by a over a factor of 2) associated correctly with the text ``Microsoft founder''. Similarly, the kernel is successful at correctly identifying the current Google CEO (Eric Schmidt) from Larry Page (Google's founder and former CEO). We also attempted to test how readily the kernel function assigned high scores for inappropriate matches by trying to pair Bill Gates as the founder of Google and Larry Page as the founder of Microsoft. The low similarity scores given by the kernel show that it does indeed find little semantic similarity between these inappropriate pairs. Once again, the kernel value is non-zero since each of the individuals is indeed the founder of some company, so the texts compared are not entirely devoid of some semantic similarity. Finally, we show that even though Larry Page has a very common surname, the kernel does a good job of not confusing him with a ``web page'' (although the cosine gives a inappropriately high similarity due to the match on the term ``page''). Lastly, we examined the efficacy of the kernel when applied to texts with multi-faceted terms - a case where we expect the raw cosine and set overlap to once again do quite poorly. As expected, the kernel does a reasonable job of determining the different facets of terms, such as identifying ``space exploration'' with ``NASA'' (even though they share no tokens), but finding that the similarity between ``vacation travel'' and ``space travel'' is indeed less than the cosine might otherwise lead us to believe. Similar effects are seen in looking at terms used in context, such as ``machine'', ``graphical'', and ``java''. We note that in many cases, the similarity values here are not as extreme as in the previous instances. This has to do with the fact that we are trying to measure the rather fuzzy notion of aboutness between semantic concepts rather than trying to identify an acronym or individual (which tend to be much more specific matches). Still, the kernel does a respectable job (in most cases) of providing a score above 0.5 when two concepts are very related and less than 0.3 when the concepts are generally thought of as distinct. Once again, the low similarity scores given by the set overlap method show that in the context of a large document collection such as the web, this measure is not very robust. As a side note, we also measured the set overlap using the top 500 and top 1000 documents retrieved for each query (in addition to the results reported here which looked at the top 200 documents as suggested in the original paper), and found qualitatively very similar results thus indicating that the method itself, and not merely the parameter settings, led to the poor results in the context of the web.
5 Theoretical Analysis of Kernel and Set Overlap Measures
In
light of the anecdotal results in comparing our kernel function
with the set overlap measure, it is useful to mathematically
analyze the behavior of each measure in the context of large (and
continuously growing) document collections such as the web. We
begin by introducing some relevant concepts for this
analysis.Intuitively, this definition captures the notion that since a search engine generates a ranking of documents by scoring them according to various criteria, the scores used for ranking may only accurately resolve document relevance to within some toleration
1 Properties of Set Overlap measure
Theorem 1 Let R(q) be the set of 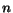 top-ranked documents with
respect to query
top-ranked documents with
respect to query  . Then, in
the set overlap measure, the expected normalized set overlap
for queries
. Then, in
the set overlap measure, the expected normalized set overlap
for queries  and
and 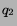 , is
, is 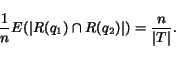
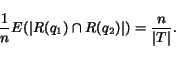
A desirable (and straightforward) corollary of this theorem, is that as we increase the results set size to capture all the relevant documents (i.e.,
2 Properties of Kernel function
Analyzing our kernel function under the same conditions as above, we find that the measure is much more robust to growth in collection size, making the measure much more amenable for use in broad contexts such as the web. Since the kernel function computes vectors based on the documents retrieved from the relevant set
Observation 2 As
 ,
then
,
then
 .
.
This observation follows directly from the fact that as
Observation 3 If queries  and
and  share the
same
share the
same  -indistinguishable
relevant set
-indistinguishable
relevant set  , then as
, then as
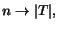 it follows that
it follows that
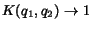 .
.
To show this observation we note that if
Theorem 2 Let
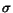 be the standard
deviation of the distribution
be the standard
deviation of the distribution  of vectors corresponding to documents in the
of vectors corresponding to documents in the
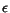 -indistinguishable
set of query results
-indistinguishable
set of query results  for queries
for queries
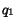 and
and 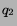 . Then, with high
probability (
. Then, with high
probability ( ), it holds
that
), it holds
that 


Note that the bound on
Theorem 3
Let 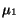 and
and 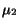 be the respective
means of the distributions
be the respective
means of the distributions  and
and  of
vectors corresponding to documents from
of
vectors corresponding to documents from  and
and  . Let
. Let
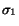 and
and 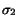 be the standard
deviations of
be the standard
deviations of  and
and
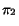 , respectively. And let
, respectively. And let
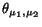 be the
angle between
be the
angle between  and
and
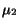 . Then, with high
probability (
. Then, with high
probability ( ), it holds
that
), it holds
that 


We note that Theorem 2 is simply a special case of Theorem 3, where
6 Related Query Suggestion
Armed with promising anecdotal
evidence as well as theoretical results that argue in favor of
using this kernel when comparing short texts, we turn our
attention to the task of developing a simple application based on
this kernel. The application we choose is query suggestion--that
is, to suggest potentially related queries to the users of a
search engine to give them additional options for information
finding. We note that there is a long history of work in query
refinement, including the previously mentioned work in query
expansion [3,13], harnessing
relevance feedback for query modification [10], using pre-computed
term similarities for suggestions [19], linguistically
mining documents retrieved in response to a search for related
terms and phrases [20,1], and even simply
finding related queries in a thesaurus. While this is certainly
an active area of work in information retrieval, we note that
improving query suggestion is not the primary focus of this work.
Thus, we intentionally do not compare our system with others.
Rather, we use query suggestion as a means of showing the
potential utility of our kernel function in just one, of
potentially many, real-world applications. We provide a user
evaluation of the results in this application to get a more
objective measure of the efficacy of our kernel. At a high-level,
our query expansion system can be described as starting with an
initial repository
|
To actually determine which of the matched queries from the repository to suggest to the user, we use the following algorithm, where the constant MAX is set to the maximum number of suggestions that we would like to obtain:
Given: user queryHere, and
list of matched queries from repository
Output: listof queries to suggest
1. Initialize suggestion list
2. Sort kernel scoresin descending order
to produce an ordered list
of corresponding queries.
3.
4. Whileand
do
4.1 Ifthen
4.1.1
4.2
5. Return suggestion list
7 Evaluation of Query Suggestion System
In order to evaluate
our kernel within the context of this query suggestion system, we
enlisted nine human raters who are computer scientists familiar
with information retrieval technologies. Each rater was asked to
issue queries from the Google Zeitgeist5 in a different month
of 2003 (since our initial repository of queries to suggest was
culled near the start of 2003). The Google Zeitgeist tracks
popular queries on the web monthly. We chose to use such common
queries for evaluation because if useful suggestions were found,
they could potentially be applicable for a large number of search
engine users who had the same information needs. Each rater
evaluated the suggested queries provided by the system on a
5-point Likert scale, defined as:
1: suggestion is totally off topic.
2: suggestion is not as good as original query.
3: suggestion is basically same as original query.
4: suggestion is potentially better than original query.
5: suggestion is fantastic - should suggest this query
since it might help a user find what they're looking
for if they issued it instead of the original query.
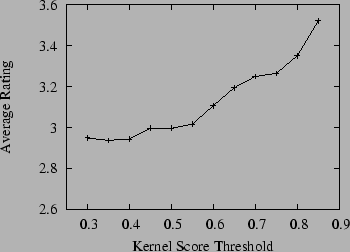
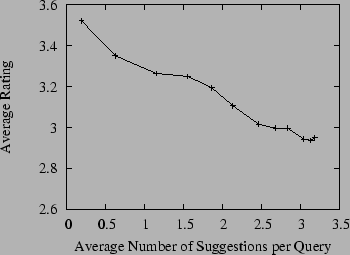
In our experiment we set the maximum number of suggestions for each query (MAX) to 5, although some queries yielded fewer than this number of suggestions due to having fewer suggestions pass the post-filtering process. A total of 118 user queries, which yielded 379 suggested queries (an average of 3.2 suggestions per query) were rated. Note that some raters evaluated a different number of queries than other raters. In Table 2 we provide an example of two user queries, the query suggestions made using our system, the corresponding kernel scores, and the human evaluation ratings for the suggested queries. As can be seen in the first example, it is not surprising that users interested in the ``california lottery'' would prefer to find winning numbers rather than simply trying to get more information on the lottery in general. In the second example, we find that users querying for ``valentines day'' may be looking to actually send greeting cards. The suggestion ``new valentine one'' is actually referring to a radar detector named Valentine One and thus is clearly off-topic with regard to the original user query. Since each query suggestion has a kernel score associated with it, we can determine how suggestion quality is correlated with the kernel score by looking at the average rating over all suggestions that had a kernel score above a given threshold. If the kernel is effective, we would generally expect higher kernel scores to lead to more useful queries suggested to the user (as they would tend to be more on-topic even given the post-filtering mechanism that attempts to promote diversity among the query suggestions). Moreover, we would expect that overall the suggestions would often be rated close to 3 (or higher) if the kernel were effective at identifying query suggestions semantically similar to the original query. The results of this experiment are shown in Figure 1, which shows the average user rating for query suggestions, where we use a kernel score threshold to only consider suggestions that scored at that threshold or higher with the original query. Indeed, we see that the query suggestions are generally rated close to 3 (same as the original query), but that the rating tends to increase with the kernel score. This indicates that queries deemed by the kernel to be very related to the original query are quite useful to users in honing their information need, especially when we allow for some diversity in the results using the post-filtering mechanism. In fact, we found that without the use of the post-filtering mechanism, the results suggested by the system were often too similar to the original query to provide much additional utility for query suggestion (although it was indicative of the kernel being effective at finding related queries).
|
8 Conclusions and Future Work
We have presented a new kernel
function for measuring the semantic similarity between pairs of
short text snippets. We have shown, both anecdotally and in a
human-evaluated query suggestion system, that this kernel is an
effective measure of similarity for short texts, and works well
even when the short texts being considered have no common terms.
Moreover, we have also provided a theoretical analysis of the
kernel function that shows that it is well-suited for use with
the web. There are several lines of future work that this kernel
lays the foundation for. The first is improvement in the
generation of query expansions with the goal of improving the
match score for the kernel function. The second is the
incorporation of this kernel into other kernel-based machine
learning methods to determine its ability to provide improvement
in tasks such as classification and clustering of text. Also,
there are certainly other potential web-based applications,
besides query suggestion, that could be considered as well. One
such application is in a question answering system, where the
question could be matched against a list of candidate answers to
determine which is the most similar semantically. For example,
using our kernel we find that: K(``Who shot Abraham Lincoln'',
``John Wilkes Booth'') = 0.730. Thus, the kernel does well in
giving a high score to the correct answer to the question, even
though it shares no terms in common with the question.
Alternatively, K(``Who shot Abraham Lincoln'', ``Abraham
Lincoln'') = 0.597, indicating that while the question is
certainly semantically related to ``Abraham Lincoln'', the true
answer to the question is in fact more semantically related to
the question. Finally, we note that this kernel is not limited to
use on the web, and can also be computed using query expansions
generated over domain-specific corpora in order to better capture
contextual semantics in particular domains. We hope to explore
such research venues in the future.
Acknowledgments
We thank Amit Singhal for many invaluable discussions related to this research. Additionally, we appreciate the feedback provided on this work by the members of the Google Research group, especially Vibhu Mittal, Jay Ponte, and Yoram Singer. We are also indebted to the nine human raters who took part in the query suggestion evaluation.Bibliography
- 1
- P. Anick and S. Tipirneni.
The paraphrase search assistant: Terminological feedback for iterative information seeking.
In Proceedings of the 22nd Annual International ACM-SIGIR Conference on Research and Development in Information Retrieval, pages 153-159, 1999. - 2
- A. Banerjee, I. S. Dhillon, J. Ghosh, and S. Sra.
Clustering on the unit hypersphere using von mises-fisher distributions.
Journal of Machine Learning Research, 6:1345-1382, 2005. - 3
- C. Buckley, G. Salton, J. Allan, and A. Singhal.
Automatic query expansion using SMART: TREC 3.
In The Third Text REtrieval Conference, pages 69-80, 1994. - 4
- N. Cristianini and J. Shawe-Taylor.
An Introduction to Support Vector Machines and Other Kernel-based Learning Methods.
Cambridge University Press, 2000. - 5
- N. Cristianini, J. Shawe-Taylor, and H. Lodhi.
Latent semantic kernels.
Journal of Intelligent Information Systems, 18(2):127-152, 2002. - 6
- S. Deerwester, S. T. Dumais, G. W. Furnas, T. K. Landauer,
and R. Harshman.
Indexing by latent semantic analysis.
Journal of the American Society for Information Science, 41(6):391-407, 1990. - 7
- I. S. Dhillon and S. Sra.
Modeling data using directional distributions, 2003. - 8
- S. T. Dumais, J. Platt, D. Heckerman, and M. Sahami.
Inductive learning algorithms and representations for text categorization.
In CIKM-98: Proceedings of the Seventh International Conference on Information and Knowledge Management, 1998. - 9
- L. Fitzpatrick and M. Dent.
Automatic feedback using past queries: Social searching?
In Proceedings of the 20th Annual International ACM-SIGIR Conference on Research and Development in Information Retrieval, pages 306-313, 1997. - 10
- D. Harman.
Relevance feedback and other query modification techniques.
In W. B. Frakes and R. Baeza-Yates, editors, Information Retrieval: Data Structures and Algorithms, pages 241-263. Prentice Hall, 1992. - 11
- T. Joachims.
Text categorization with support vector machines: learning with many relevant features.
In Proceedings of ECML-98, 10th European Conference on Machine Learning, number 1398, pages 137-142, 1998. - 12
- J. S. Kandola, J. Shawe-Taylor, and N. Cristianini.
Learning semantic similarity.
In Advances in Neural Information Processing Systems (NIPS) 15, pages 657-664, 2002. - 13
- M. Mitra, A. Singhal, and C. Buckley.
Improving automatic query expansion.
In Proceedings of the 21st Annual International ACM-SIGIR Conference on Research and Development in Information Retrieval, pages 206-214, 1998. - 14
- V. V. Raghavan and H. Sever.
On the reuse of past optimal queries.
In Proceedings of the 18th Annual International ACM-SIGIR Conference on Research and Development in Information Retrieval, pages 344-350, 1995. - 15
- G. Salton and C. Buckley.
Term weighting approaches in automatic text retrieval.
Information Processing and Management, 24(5):513-523, 1988. - 16
- G. Salton and M. J. McGill.
Introduction to Modern Information Retrieval.
McGraw-Hill Book Company, 1983. - 17
- G. Salton, A. Wong, and C. S. Yang.
A vector space model for automatic indexing.
Communications of the ACM, 18:613-620, 1975. - 18
- A. Vinokourov, J. Shawe-Taylor, and N. Cristianini.
Inferring a semantic representation of text via cross-language correlation analysis.
In Advances in Neural Information Processing Systems (NIPS) 15, pages 1473-1480, 2002. - 19
- B. Vélez, R. Wiess, M. A. Sheldon, and D. K. Gifford.
Fast and effective query refinement.
In Proceedings of the 20th Annual International ACM-SIGIR Conference on Research and Development in Information Retrieval, pages 6-15, 1997. - 20
- J. Xu and W. B. Croft.
Query expansion using local and global document analysis.
In Proceedings of the 19th Annual International ACM-SIGIR Conference on Research and Development in Information Retrieval, pages 4-11, 1996.
Footnotes
- ... billion1
- Leading search engines claim index sizes of at least 20 billion documents at the time of this writing.
- ... snippet2
- While the real focus of our work is geared toward short
text snippets, there is no technical reason why
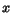 must have limited length,
and in fact
must have limited length,
and in fact  can be arbitrary
text.
can be arbitrary
text. - ... terms.3
- We prefer the term multi-faceted over ambiguous, since multi-faceted terms may have the same definition in two contexts, but the accepted semantics of that definition may vary in context. For example, the term ``travel'' has the same definition in both the phrases ``space travel'' and ``vacation travel'', so it is (strictly speaking) not ambiguous here, but the semantics of what is meant by traveling in those two cases is different.
- ... arbitrary4
- The distribution
 is
arbitrary up to the fact that its first two moments, mean and
variance, exist (which is a fairly standard and non-restrictive
assumption).
is
arbitrary up to the fact that its first two moments, mean and
variance, exist (which is a fairly standard and non-restrictive
assumption). - ... Zeitgeist5
- http://www.google.com/intl/en/press/zeitgeist.html