XML document clustering
aims to group XML documents into different clusters with a
standard of document similarity. Much previous work has
explored clustering methods for grouping structurally similar
XML documents so as to find common structures or DTDs for
various purposes. While in this study we focus on grouping
topically similar XML documents, i.e., the text contents of the
XML documents within a cluster express a similar topic or
subject. Based on the traditional Vector Space Model (VSM), XML
documents are processed as ordinary unstructured documents by
removing all element tags and thus the structural information
is totally lost. Another intuitive method takes into account
the structural information by computing the similarity of texts
within each element respectively and then combining these
similarities linearly, which is called C-VSM. Much work [1, 4]
explores this problem by extending VSM in order to incorporate
the element tag information. For SLVM proposed in [4], each document, docx, is
represented as a matrix ![]() , given as
dx=<dx(1),dx(2),ˇ,dx(n)>T,
dx(i)=<dx(i,1),dx(i,2),ˇ,dx(i,m)>, where
m is the number of XML elements, and n is the number of terms.
, given as
dx=<dx(1),dx(2),ˇ,dx(n)>T,
dx(i)=<dx(i,1),dx(i,2),ˇ,dx(i,m)>, where
m is the number of XML elements, and n is the number of terms. ![]() is a feature
vector related
to the term
tBiB for
all the elements, dBx(i,j)B is a
feature related to
the term tBiB and
specific to the
element eBjB, given
as dx(i,j)=TF(ti,docx.ej)*IDF(ti) and TF(ti,docx.ej) is the
frequency of the term tBiB in
the element eBjB of
the documents docBxB.And each
dBx(i,j)B is
normalized by
is a feature
vector related
to the term
tBiB for
all the elements, dBx(i,j)B is a
feature related to
the term tBiB and
specific to the
element eBjB, given
as dx(i,j)=TF(ti,docx.ej)*IDF(ti) and TF(ti,docx.ej) is the
frequency of the term tBiB in
the element eBjB of
the documents docBxB.And each
dBx(i,j)B is
normalized by ![]() . The similarity between two documents docBxB and
docByB is then defined
with an
element semantic
matrix
Me
introduced, given
as
. The similarity between two documents docBxB and
docByB is then defined
with an
element semantic
matrix
Me
introduced, given
as
![]() (1)
(1)
where MBeB is an m*m element semantic matrix which captures both the similarity between a pair of XML elements as well as the contribution of the pair to the overall document similarity.
The popular way to determine the value of MBeB is based on the edit distance [5]. In order to acquire a more appropriate element semantic matrix, with the notion that term similarity should be affecting document similarity and vice versa, we propose aniterative algorithm for learning the element semantic matrix MBeB, given as
![]() (2)
(2)
![]() (3)
(3)
![]() represents a set of XML documents,
where
represents a set of XML documents,
where![]() is a matrix with its
kPthP column corresponding to dBk(iBB)B of
the k-thPP document and p is the
number of documents.
is a matrix with its
kPthP column corresponding to dBk(iBB)B of
the k-thPP document and p is the
number of documents.![]() . All the entriesˇŻ values of matrix
SBdB are
normalized between
zero and one. Two totally different documents have a similarity
value of
zero and two identical
documents have a similarity value of one. An additional
constraint for getting a non-trivial solution
of having both matrices
with all zero elements is required to force the diagonal elements of
SBdB (i.e., the similarity of identical documents) to take
the value of one.
. All the entriesˇŻ values of matrix
SBdB are
normalized between
zero and one. Two totally different documents have a similarity
value of
zero and two identical
documents have a similarity value of one. An additional
constraint for getting a non-trivial solution
of having both matrices
with all zero elements is required to force the diagonal elements of
SBdB (i.e., the similarity of identical documents) to take
the value of one.
VSM does not consider structural information and C-VSM only allows the text within an element of one document to correspond to the text within the same element of the other document. The two cases ignore the semantic relationship between different elements and have ˇ°under-contributionˇ± problem. SLVM overcomes the above ˇ°under-contributionˇ± problem by allowing the text within an element of one document to correspond to the text within any element of the other document. However, the corresponding relation between elements is loose, i.e. the text with a weight within an element of one document can always use its total weight to correspond to the text within any element of the other document, which is believed to have the so-called ˇ°over-contributionˇ± problem.
In order to address the above problems of ˇ°under-contributionˇ± and ˇ°over-contributionˇ±, illuminated by the Proportional Transportation Distances [2], we propose the Proportional Transportation Similarity (PTS) to measure the document similarity. PTS allows the text within an element of one document to correspond to the text within any element of the other document under a few strict constraints by modeling a transportation problem in the linear programming field. The document similarity over one single term is computed as follows:
Given two feature vectorsdx(i)=<dx(i,1),dx(i,2),ˇ,dx(i,m)>B Band dy(i)=<dy(i,1),dy(i,2),ˇ,dy(i,m)>, related tothe particular term tBiB for all the elements in documents docBxBand docBy Brespectively, where m is the number of elements, a weighted graph G is constructed as follows:
Let dx(i)=<dx(i,1),dx(i,2),ˇ,dx(i,m)> as the weighted point set for the term tBiB in document docBxB, dBx(i,j)B is a feature related to the term tBiB and specific to the element eBj B given as the TF(ti,docx.ej)*IDF(ti) value.
Let dy(i)=<dy(i,1),dy(i,2),ˇ,dy(i,m)> as the weighted point set for the term tBiB in document docByB, dBy(i,j)B is a feature related to the term tBiB and specific to the element eBj B given as the TF(ti,docy.ej)*IDF(ti) value..
Let
G={dBx(i)B, dBy(i)B, Me}
as a weighted graph constructed by dBx(i)B, dBy(i)B, and Me. V=dx(i)ˇČdy(i) is the vertex set while Me
is the edge
matrix, either learned or
obtained based on edit distance. ![]() ,
, ![]() are the
total weights of dx(i), dy(i), i.e. the sums of all weights of points within
dx(i), dy(i), respectively.
are the
total weights of dx(i), dy(i), i.e. the sums of all weights of points within
dx(i), dy(i), respectively.
Based
on the weighted
graph G , the
possible flows![]() =
[fBuvB],
with fBuvB the flow
from dx(i,u)to dy(i,v), are defined by the following constraints:
=
[fBuvB],
with fBuvB the flow
from dx(i,u)to dy(i,v), are defined by the following constraints:
![]()
![]()
![]() (4)
(4)
![]()
![]() (5)
(5)
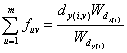
![]() (6)
(6)
![]() (7)
(7)
Constraint (4) allows moving weights from dBx(i)B to dBy(i)B and not vice versa. Constraint (5) and (7) force all of dBx(i)BˇŻs weight to move to the positions of points in dBy(i)B. Constraint (6) ensures that this is done in a way that preserves the old percentages of weight in dBy(i)B.
And PTS is given by
![]() (8)
(8)
The overall document similarity based on PTS is obtained as
![]() (9)
(9)
The above transportation problem can be efficiently solved by interior-point algorithms [3] which have polynomial time complexity.
In the experiments, we use the agglomerative hierarchical clustering (AHC) algorithm as the cluster engine. Three benchmarking datasets with different sizes extracted from ACM SIGMOD Record 19991, which is composed of hundreds of documents from past issues of SIGMOD Record, are used for evaluation. The class each record belonging to is given by the ˇ°categoryˇ± tag2. The weighted F-measure is used as the evaluation metric. Table 1 gives the results. For SLVM and PTS, either the edit distance approach or the learning method can be employed to acquire element semantics, the corresponding results are given in different columns respectively.
Table 1. F-measure (%) comparison results
| Data Set | VSM | C-VSM | SLVM(Edit Distance) | SLVM(Learned Semantics) | PTS(Edit Distance) | PTS(Learned Semantics) |
|---|---|---|---|---|---|---|
| ACM-8 | 40.0 | 36.9 | 46.0 | 53.0 | 43.3 | 58.9 |
| ACM-12 | 21.2 | 22.4 | 24.2 | 43.0 | 22.9 | 46.6 |
| ACM-16 | 42.4 | 47.7 | 38.8 | 58.8 | 35.1 | 69.9 |
Seen from the above table, the proposed PTS with learned element semantics performs best over all three data sets. The approaches with the learned element semantics, i.e. SLVM and PTS, both significantly outperform the traditional approaches not considering the element semantics, i.e. VSM and C-VSM, which shows the importance of incorporating the element semantics for XML document clustering. For SLVM and PTS, we find that the performance based on the learning method for acquiring the element semantics is significantly better than that based on the edit distance approach, which demonstrates that the learned element semantics can reflect the true underlying semantics between XML elements.
The experimental results demonstrate that with the appropriate element semantics, PTS can improve the performance by circumventing both the ˇ°over-contributionˇ± problem and the ˇ°under-contributionˇ± problem.
[1] A. Doucet, H. A. Myka. Naive Clustering of a Large XML Document Collection. In Proceedings of the 1st INEX, Germany, 2002.
[2] P. Giannopoulos and R. C. Veltkamp. A Pseudo-Metric for Weighted Point Sets. In Proceedings of the 7th European Conference on Computer Vision (ECCV) , 715¨C730, 2002.
[3] N. Karmarkar. A new polynomial-time algorithm for linear programming. In Proceedings of the Sixteenth Annual ACM Symposium on Theory of Computing , 302-311, 1984.
[4] J.W. Yang and X.O. Chen. A semi-structured document model for text mining. Journal of Computer Science and Technology, 17(5): 603-610, 2002.
[5] K. Zhang and D. Shasha. Simple fast algorithms for the editing distance between trees and related problems. SIAM J. Comput., 18(6):1245¨C1262, 1989.
1 http:/www.acm.org/sigs/sigmod/record/xml/XMLSigmodRecordMar1999.zip
2 All the ˇ°categoryˇ± tags as well as the inner texts and the corresponding descriptions in the record are removed to make the answer class blind to the clustering algorithm.