
Figure 1. A fragment of author.xml

Figure 2. A fragment of book.xml
Symmetrically Exploiting XML
Shuohao Zhang and Curtis Dyreson
Washington State University
PO Box 642752
Pullman, WA 99164, U.S.A.
{szhang2, cdyreson}@eecs.wsu.edu
ABSTRACT
Path expressions are the principal means of locating data in a hierarchical model. But path expressions are brittle because they often depend on the structure of data and break if the data is structured differently. The structure of data could be unfamiliar to a user, may differ within a data collection, or may change over time as the schema evolves. This paper proposes a novel construct that locates related nodes in an instance of an XML data model, independent of a specific structure. It can augment many XPath expressions and can be seamlessly incorporated in XQuery or XSLT.
Categories and Subject Descriptors
H.2.1 [Database Logical Design] Subjects: Data models.
H.2.3 [Database Languages] Subjects: Query Languages.
General Terms
Algorithms, Languages.
Keywords
XML, Path Expressions, XPath, XQuery.
In 1970, E. F. Codd proposed a relational model of data to replace the popular (at that time) hierarchical model [3]. Codd critiqued the hierarchical model because it did not support the symmetric exploitation of data.[1] The hierarchical model used asymmetric path expressions to locate data. A path expression is a specification of a path (or a set of paths) in a hierarchy. Path expressions are asymmetric because they depend on how the data in the hierarchy is structured and the same data can be organized in different hierarchies. Codd presented five reasonable hierarchies for a simple part/supplier data collection and demonstrated that, in general, a path expression formulated with respect to one hierarchy would fail on some other hierarchy.
It is generally accepted that Codd won the debate with the hierarchical model as evidenced by the current industrial dominance of relational database management systems. But thirty-five years later a hierarchical data model has resurfaced with the advent of XML [14]. XML data models are tree-like, hierarchical models. As a consequence, asymmetric path expressions have reappeared in XML query languages. The core of most XML query languages is a path language to navigate to various places in a hierarchy. For XQuery the path language is (a subset of) XPath. Asymmetric path expressions make queries brittle in the sense that a query might fail to produce the desired result if the structure changes or if it is executed on the same data organized in a different hierarchy.
There are four scenarios where symmetric exploitation of hierarchical data is particularly attractive: lack of schema knowledge,heterogeneous data, irregular data, and schema evolution. First, detailed knowledge of the data's structure or schema is often needed in order to correctly formulate a path expression. Many data collections lack a schema, and even when a schema is present, it may be complex and difficult to decipher for some users. The ability to query data without knowing its specific structure would be useful for both expert and casual users. Second, there is the increasing need for data integration. It is becoming common to pull data from different sources into a single data collection. Each source could organize similar data in a different hierarchy. If queries are not symmetrically exploitable, then a single logical query over the heterogeneous hierarchies would potentially require different path expressions for each structure. Third, the decentralized nature of the web has facilitated a growth in the generation and exchange of data authored by casual users. More often than not, data provided by these users does not conform to a strict schema; rather the data in a single collection is irregularly structured. Last, even in a centralized database with a single, simple, well-defined schema, shifts in business strategy and corporate environments sometimes engender evolution in how data is organized. Legacy path expressions that depend on a particular hierarchy may no longer work when a schema evolves.
A common theme underlying the various scenarios above is that the asymmetric nature of path expressions makes them brittle. This paper proposes a novel extension to XPath to support the symmetric exploitation of XML data. We extend XPath with a symmetric locator. This extension allows a user to query XML data without knowing its exact structure in many situations. That is, a user simply needs to know the names of relevant elements and attributes and their possible relationships to properly formulate a query. The extension is simple in syntax and semantics. Specifically, we introduce a new axis: the closest axis, which locates nodes that are closest to a context node. In abbreviated syntax the closest axis is represented by a "->" operator, so the expression $n->t locates all nodes of type t "closest to" the node bound by $n. Remarkably, this simple operator can replace asymmetric steps in path expressions in many XQuery queries written for daily tasks.
This paper is organized as follows. A motivating example is presented in Section 2. Section 3 defines the syntax of the closest axis, while Section 4 describes its semantics. We consider both in-memory and persistent implementations in Section 5. Section 6 illustrates the use of the closest axis by rewriting some of the queries in the XML Query Use Cases [16]. Section 7 discusses related work and Section 8 concludes the paper.
Consider how a collection of bibliographic information such as authors, books and publishers may be represented in a hierarchy. One of (but not limited to) the following two hierarchies may be used: 1) the hierarchy contains a list of authors, each of which contains a list of books by that author, or 2) the hierarchy contains a list of books, each of which contains a list of authors of that book. As an example, consider some bibliographic data about the author E. F. Codd that involves two books and two publishers. The two different representations are captured by two XML documents, author.xml and book.xml, shown respectively in Figure 1 and Figure 2. Both documents contain the same data but they have different structures.
For some queries, different path expressions are needed to query each hierarchy. For example, consider a query to retrieve books by E. F. Codd. The XQuery query for author.xml is given below.
return doc("author.xml")/author[name= 'E. F. Codd']/book
This query uses a path expression that navigates from the root to the proper author elements and then finds the desired book. But this query does not work for book.xml since it has a different structure. To query book.xml a different query has to be formulated.
return doc("book.xml")/book[author/name='E. F. Codd']
The path expression in each query differs. Moreover, no single path expression suffices to locate the desired data in both hierarchies.
While asymmetric path expressions are wedded to a particular hierarchy, the key to developing a symmetric locator is to identify what is invariant across the same data organized in different hierarchies. Observe that in both Figure 1 and Figure 2, book titles by an author are closest to that author. Here "closeness" is the distance on the path between nodes in the hierarchical model of an XML document. In both hierarchies the author E. F. Codd is the closest author to each of the titles. This is not something specific to <author>s and <title>s only. In fact, whenever two nodes are closest in Figure 1, so are their counterparts in Figure 2.
This invariant property of different hierarchies can be exploited with a symmetric locator that locates related information based on closeness rather than a specific path. The symmetric locator is a closest axis. In abbreviated syntax the axis is denoted by an operator "->". Semantically, the axis locates all nodes that are closest to the context node. So "$n->t" returns a sequence of all t nodes closest to the node bound by $n. With this operator, the query posed at the beginning of this section can be expressed as follows:
return doc("any.xml")->author[->name='E. F. Codd']->book
where any.xml could be either author.xml or book.xml. It can also be applied to a hierarchy that, for example, contains a list of publishers, each of which contains a list of books. Furthermore, the query works for data with a heterogeneous structure. Suppose we mix bibliographic data from multiple sources (say, from the hierarchy of Figure 1 and that of Figure 2), the same query would work without any change. In contrast, it would be cumbersome to formulate a query using asymmetric path expression to query heterogeneous data. The user first has to know which structures are present in the data, and then write a different path expression for each distinct structure. Complicated as it is, such a query could only handle those hierarchies taken into account, and may need to change whenever data from another source (with a different structure) is added to the collection. In summary, the closest axis is more convenient to formulate and more robust against structural changes than asymmetric path expressions.
Although the closest axis is intended to replace asymmetric XPath axes in many practical uses, it cannot replace all of them. Without the sophisticated navigational functionalities provided by asymmetric path expressions, a query language may be less than Turing-complete [7]. When path expressions are inevitable for a task, one still needs to resort to XPath. (See Section 6 for more discussion on this.) So it is important to remember that the closest axis extends but does not replace path expressions.
The closest axis has a very simple syntax that can be seamlessly integrated into XPath. Figure 3 shows the EBNF grammar for the axis, where the newly-introduced symbols are underlined.
[29'] AxisStep ::= (ForwardStep | ReverseStep | ClosestStep) PredicateList
[n1] ClosestStep ::= ClosestAxis NodeTest | AbbrevClosestStep
[n2]
ClosestAxis ::= <"closest"
"::">
[n3] AbbrevClosestStep ::= "->" NodeTest
Figure 3. EBNF grammar for the extended XPath
This grammar extends the current XPath grammar defined in the W3C candidate recommendation "XML Path Language (XPath) 2.0" [15]. There are 73 rules in the current XPath grammar, among which only rule [29] has to be modified. The modified rule, annotated [29'], introduces a new step, ClosestStep. ClosestStep is further defined by the new rule [n1]. A ClosestStep may or may not be abbreviated. New rules [n2] and [n3] define the unabbreviated and abbreviated syntax, respectively. An unabbreviated step is in the form closest::NodeTest, and an abbreviated step is ->NodeTest. The new XPath grammar has a total of 76 rules, with one of the original rules modified and three added.
This section presents the formal semantics of the closest axis. We first present a data model for XML documents, and then define the closest axis. The specific semantics of the axis depends on the important concept of node "type". We also discuss a technique that computes node type in the absence of data schema.
XML documents are commonly modeled as ordered, labeled trees. We first define such an XML data model.
Definition [tree] A tree is a tuple (V, E, Σ, L, C, T), where
• V is the node set. r∈V is a special node called the root of T,
• E⊆V?i>V is the edge set such that there is a path between every pair of nodes, there is no cycle among the edges, and edges that share a common node - called the parent of the other node (the child) in each such edge - are ordered,
• Σ is an alphabet of labels and text values,
• L:V→Σ is a label function that maps each node to its label,
• C:V→Σ∪{ε} is a value function that maps a node to its value, in which C(v)=εif node v has an empty value, and
• T:V→S is a type function that maps each node to a type, which is a value in the type set S. ♦
This tree data model is a stripped-down version of the Document Object Model (DOM) [13]. Though the model is simple it is sufficient for our purposes in this paper. Elements are represented by nodes in our tree data model. Other kinds of nodes in the DOM such as attributes and comments are ignored.[2]
The label function maps each node to its label, that is, its element tag. So a <book> node would map to the label book.
The type function refines the label function by possibly partitioning the nodes associated with the same label into different types. The type function specifies the type of each node. There are several ways that the type could be computed. If a schema is available, then the type of a node might be given by an element type definition in the schema. For instance a <name> element type definition might provide the type for author names, while publisher names resolve to a different type even though they share a common label. When a schema is unavailable, the simplest case is to make the type and label functions the same. That is, nodes are typed by their labels. Because the type plays an important role in the definition of the closest axis, Section 4.3 and Section 4.4 give two more refined methods of computing the type in the absence of a schema.
Ordering of elements is important for XML. We adopt the common document order which orders nodes in a tree data model based on the first appearance of the corresponding text in the document. In author.xml, for example, text fragment <name> appears earlier than both occurrences of <book>. Hence, the name node precedes the book nodes in the tree data model.
As introduced in the motivating example in Section 2, the closest axis is used to locate "the closest nodes" to the context node. Whether a node is close or far depends on a distance metric as defined below.
Definition [distance] Suppose (V, E, Σ, L, C, T) is a tree and u, v∈V. The distance between u and v, denoted dist(u,v), is the number of edges on the shortest path between u and v. ♦
In a tree, the shortest path between two nodes is unique. The distance between the nodes is measured by the length of this path.[3]
The closest axis evaluates to the sequence of nodes that are closest to the context node.
Definition [the closest axis] Suppose (V, E, Σ, L, C,T) is a tree and c∈V is the context node. Then the closest axis is defined as follows.
closest(c) = [d1 , ... , dn], where
• d1 , ... , dn∈V,
• ∀i, 1 ≤ i ≤ n, ∀x, y∈V,
L(x) = L(di) ∪ T(y) = T(c) ⇒ dist(c, di) ≤ dist(y, x); (i)
• ∀i, j, 1 ≤ i < j ≤ n, di precedes dj in document order. (ii) ♦
The closest axis is defined as a function that takes a context node c and returns a node sequence. The function has two primary conditions. First, the node ordering condition (ii) states that the result preserves the original document order. Second, the node selection condition (i) constrains the nodes that appear in the result. The condition stipulates that a node is in the result if it is the closest node of a particular label to the context node, but that the distance to the closest node is within the minimal distance of a node of the same type as the context node to a node of the same label as a node in the result. The intuition is that the closest axis seeks out all the nodes of each different label that are closest to the context node, but restricts the search based on the minimal possible distance between a given type and a given label.
To better understand the meaning of the node selection condition, let's consider an example. Figure 4 shows the hierarchy for the XML given in Figure 1. Assume that the type of each node is its label. Let the context node be the leftmost title node. The nodes closest to the title node are pointed to by dashed arrows. The five closest nodes are ordered in the closest axis in document order. In this example there is only one node of each label that is closest, but in general there could be several nodes with the same label that are closest. Note that none of the nodes in the other book subtree is closest to this title.
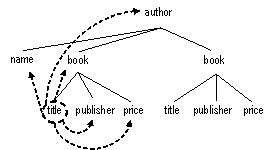
Figure 4. Nodes closest to the first title
In the above example, the node selection condition in the axis definition could in fact be simplified to the following
∀i, 1 ≤ i ≤ n, ∀x∈V, L(x) = L(di) ⇒ dist(c, di) ≤ dist(c, x) (i')
in which the types are absent.
This simplification is possible because the tree is of a regular structure. We say that the tree's structure is regular if the following holds
∀c∈V, ∀l∈Σ, ∃v∈V such that
L(v) = l ∧ dist(c, v) = min{ dist(y, x) | L(x) = l∧ T(y) = T(c)}.
That is, for any node c and any label l in a regular tree, we can always find a node v labeled l such that c and v are of the minimal distance of nodes typed T(c) and nodes labeled l. The fact that every node is guaranteed to have a minimal distance node of any given label reduces (i) to (i').
For hierarchies that are not regular, the node selection condition (i) is more appropriate than the simplified version (i'). For example, suppose that the first book does not have a price child, as shown in Figure 5. Here the label and type are still the same; but the tree is irregular in the sense that the context title node could not find a label price node within the minimal distance of all possible pairings of type title node and label price node, which is two. The closest axis using condition (i') (just the labels) would locate the price child of the second book since it is the closest price. But this price should not belong to the closest axis of the first book because it is closer to the second book than the first.

Figure 5. The search is restricted by the type information
In the trees in Figure 4 and Figure 5, the label and type functions are the same. But there are scenarios where nodes of the same label should be differentiated for the results to be intuitively appropriate. For example, the price of a book and the price of a car need to have different types. Suppose the closest node labeled name to car price is four while the closest node labeled name to book price is three. If all price nodes were of the same type, then no car price would have any name node in its closest axis. By distinguishing the two types of price nodes, a car price node can include in its closest axis all name nodes at a distance of four. Note that the book price's axis contains author name, while the car price's axis probably contains owner or dealer name, a different type of name. But the node selection condition (i) is concerned with type of the context node only, but not the type of the nodes in the axis.
Our use of the term "closest" to describe the new axis is evocative but imprecise. For some data collections, the results may be counterintuitive. For example if an author name node is equi-distant from both a book price type and a car price type (an unlikely scenario, but possible) then the closest axis of this node includes nodes of both type book price type and car price. So while the closest axis can be used to symmetrically exploit data, the meaning of the axis depends on the data.
The closest axis is similar to the current XPath axes insofar as it returns a node sequence relative to a context node. A node test and predicates can be further applied to filter the sequence. Unlike all other axes, the closest axis is a non-directional axis. That is, it does not locate nodes in a particular direction (up, down, left, right) in the hierarchy. Instead it utilizes node and type information to find nodes that are close to the context node in any direction. Only non-directional axes can symmetrically exploit data.
An interesting consideration is whether nodes connected by ID/IDREF relationships can be considered as closest nodes. In a tree, there would be no edge between two such nodes, so the two nodes would not be closest. But we could easily add a "virtual" edge to connect such nodes and compute distances in the resulting graph. However, in the interest of simplicity we do not consider such virtual edges in this paper.
Node type is important in determining which nodes are in the closest axis. The use of types takes into account the fact that different kinds of real-world entities may be represented by nodes of identical labels in a tree. So a proper type function T should for example distinguish a book price from a car price.
The type function can sometimes be easily inferred when the data is accompanied by schema information in the form of DTD or XML Schema. But a common situation is that we do not know the schema. We now introduce a technique to compute the types in the absence of a schema. The node types produced by these are potentially helpful in refining the possible results of a closest axis.
Definition [root-to-node path type] A tree (V, E, Σ, L, C, T) uses root-to-node path type, or path type in short, if for anyv∈V, T(v) is a list of the labels of the nodes on the inclusive path from the root r to v. ♦
The path type is essentially a concatenation of the labels of the nodes from the root to the node. With path type, nodes of the same type always have the same label, but not vice versa. The rationale behind path type is the following claim:
If two nodes are of the same type, then their respective child nodes with the same label should be of the same type too.
It is rather common for two nodes in a tree to have the same label but represent different kinds of entities. However, it is rarely the case that such two nodes' respective parents have the same type. In our previous example of book price and car price, suppose their respective parents are book and car. The paths from the root node to a book price node and a car price node are different; therefore book price and car price have different path types.
Path type can be efficiently computed when the tree is parsed. The type of a node is obtained by appending its own label to the end of the path type of its parent. The complexity of the computation is O(n) where n is the number of nodes in the tree.
The signature type is also useful in specifying queries with the closest axis. Furthermore, it is crucial to the efficient implementation of the closest axis.
We first introduce the concept of signature. A signature is a succinct description of the structure of a data forest, similar to a Data Guide.
Definition[signature] Denoted sig(F), the signature of a forest F is a forest such that
• C(v) = ¦Å for every node v in sig(F);
• if F is a tree that consists of a root r and forest S (the root of each tree in S is connected to r by an edge), then sig(F) is a tree that consists of a root node labeled L(r) and the forest sig(S) (if F consists of a single node r, then sig(F) contains a single node as well);
• if F is a forest that consists of n trees H1,..., Hn (n>0), thensig(F) consists of a set of trees: sig(H1),..., sig(Hk), where Hi∈{H1,...,Hn} (1≤i≤k) and {sig(Hi)|1≤i≤k}={sig(Hi)|1≤i≤n}; tree equivalence is defined in terms of isomorphism between labeled trees. ♦
A signature summarizes the structure of a forest. A signature tree never contains two sibling subtrees that are isomorphic.
For example, the tree in Figure 4 (the tree data model of author.xml in Figure 1) has the signature shown in Figure 6. This signature is smaller in size than the data. The data tree contains two book subtrees of identical structure - each book node has title, publisher and price children, all of which are leaf nodes. Keeping one copy of this book structure in the signature tree is sufficient to capture the structure of the data tree.
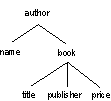
Figure 6. Signature of author.xml
A signature is unlike a schema specification such as a DTD. Any forest has exactly one signature, but could potentially conform to many schemas. Also, a schema usually precedes the data. Data is created in a structure that conforms to the given schema. Users normally have to know about the schema to query the data. In contrast, a signature is computed from the given data to assist the evaluation of the closest axis. Hence a signature is preceded by the data.
A signature can be computed efficiently. The definition of signature gives a recursive algorithm that computes it.
Usually the signature will be much smaller than the data, especially for large data collections since many data items will share a common structure. But in the worst case, they are the same size.
Finally, we extend the concept of signature from trees to nodes.
Definition [node signature] The signature of a node v in a data tree is the signature of the tree rooted at v. ♦
Node signature is compatible with tree signature. The signature of a tree is just the node signature of the root node.
Observe that there is a correspondence between nodes in a data tree and nodes in the signature tree. We can define the type of a node in a data tree as its corresponding node in the signature.
Definition [signature type] Suppose sig(F) = S. The signature type of a node in F is its corresponding node in S. ♦
Because a tree signature is recursively computed in a bottom-up fashion, node signature is simultaneously determined while computing the signature of the whole tree. As the pre-condition for the node classification algorithm, we assume that node signature of each node is already available, represented by a the function sig(). The algorithm is listed in Figure 7.
The algorithm computes signature type for all nodes by invoking the recursive function visit() on the root of the data tree. It starts with the obvious base condition: the root of a tree is mapped to the root of its signature tree. It then recursively computes the type of each node in a top-down fashion. At a node n in the data tree, the function returns if n has no child; otherwise, it decides the type of each of its child by comparing the signature of this child to the each of the child subtree of T(n), the node in the signature tree that n corresponds to. (Note that in the algorithm, the tree rooted at s is equivalent to sig(s), because a signature tree does not contain isomorphic sibling trees.) Once the type of a child c is determined, visit(n) calls visit(c) recursively. Here the most costly part is to determine isomorphism between trees. As mentioned before, comparing unordered trees can be efficiently computed with the help of a sort.
Figure 7. An algorithm for computing node type
This section investigates how the closest axis can be efficiently computed. At first sight, it seems quite probable that the evaluation of the closest axis would be completely different from that of a usual XPath axes. Axes like descendent are directional, while the closest axis is non-directional; its semantics just describes the property of the closest nodes without giving a specific direction to where it is located.
XPath/XQuery implementations can be broadly classified as either in-memory or persistent. We present both in-memory and persistent implementations in this section. An in-memory implementation loads the entire data tree into memory and evaluates the axis directly on the tree. However, some data collections are too large for memory. In a persistent implementation, the data resides predominately on disk. Indexes are commonly used in persistent implementations to optimize performance by reducing the number of blocks read from disk during query evaluation.
The closest axis can be naïvely implemented by exploring from the context node in all directions until each kind of label is reached that is within the minimal distance between the type of the label and the type of the context node. Such an evaluation simply has to enumerate all the possible paths starting from the context node to look for the closest node(s). The algorithm that computes all the closest nodes to a context node, v, is shown in Figure 8.
Though the naïve algorithm computes the closest axis it has high cost. The algorithm explores maxDistance edges from the context node, potentially covering the entire tree.
Figure 8. A naïve, in-memory algorithm for evaluating the closest axis
Further, the naïve algorithm assumes the existence of a typeDistance hash table that has already computed the minimal distances between pairs of types. This table can be constructed when a DOM is built or just prior to evaluating the axis using the signature described in Section 4.4.1. Essentially, the strategy is to evaluate the closest axis in the signature forest to find all of the types closest to the type of the context node. For example, in the evaluation of the closest axis from the first title node in Figure 4, the signature shown in Figure 6 could be explored to determine the distance from the title type to the closest types corresponding to each label.
We anticipate that the closest axis will almost always be used with a node test for a specific label, e.g., "closest::price." (See Section 6 for closest axis use cases). The evaluation cost can be significantly reduced in such cases. One way to reduce the cost in the naïve algorithm is to set the maxDistance to the distance of the type corresponding to the label in the node test, e.g., price in the example given above. On average this will cut the cost in half. However, a significantly better strategy is possible.
The better strategy is to convert the non-directional search to a directional search. Observe that a signature provides both a distance and a path to the desired type. To continue with the example, assuming that the context node is a title type, a single path connects the price type to the title type in the signature. The path climbs to the book parent and then drops to the price child. In general, the path between any two types traverses through the least common ancestor (LCA) of the two types in the signature. So the optimization is to replace the closest axis with a different expression that follows the path to the nodes specified by the node test. In the example, the non-directional expression "closest::price" would be replaced with the following directional path expression: "parent::*/child::price." The conversion can be performed by a pre-processor prior to evaluating an expression, or the directional path expression can be substituted during evaluation of a closest axis. Note that in general, there might be several closest types, so a union path expression that follows all of the paths might be needed.
For the closest axis to be of practical value for database applications, it needs to be computed efficiently in persistent implementations. Since the axis will almost always be used in combination with a non-wildcard node test, we focus on the implementation of the node test optimization and introduce an LCA-join operation that efficiently evaluates the closest axis.
Many XPath/XQuery implementations use a node numbering scheme and indexes to quickly evaluate queries. (Related work is discussed in Section 7.) As an example, consider the following scheme. Given a tree, assign each node a number according to its ordinal in document order. The numbers range from 1 to n, the total number of the nodes. This can be achieved by a preorder traversal of the tree. Each node is also assigned the number of its maximum descendent. This allows ancestor/descendent relationships to be determined by reasoning about the node numbers. All nodes with a number larger than the number of a node v and no larger than its maximum descendent's are descendents of v. Figure 9 shows the numbering for the data tree of author.xml in Figure 1. The first book node has the number 3 and its maximum descendent is 6. So its descendents are all the nodes numbered between 3 and 6.
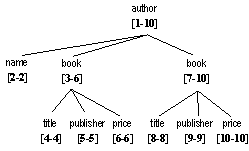
Figure 9. Numbering the data tree of author.xml
Next, an index of types is created. The index maps each type in the signature to an ordered list of node numbers for nodes of that type. Then the closest axis can be computed by simply merging three lists as depicted in Figure 10. The list merging is an LCA-join. In the figure, there are three lists of nodes: parents, children, and least common ancestors (lca in short). The parents list is the list of context nodes (we assume that these nodes are all of the same type, if not then each type in the list will be joined in a separate LCA-join). The children list contains the nodes in the closest type to the type of the context nodes. The lca list is the list corresponding to the label that is the least common ancestor of the child and parent labels in the signature. For instance, for title children and publisher parents in Figure 6, the lca is book. The lists are merged in the direction of a lexical ordering of the data (from left to right in the figure). A parent is closest to a child if both are descendent of the same lca. If a parent is not a descendent of the current lca, then either the current lca is before the current parent (child), in which case the current lca pointer is advanced, or the current parent (child) is before the current lca, in which case the current parent (child) pointer is advanced. Typically only two lists are merged instead of three since the parent or child is the lca.
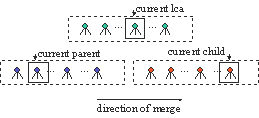
Figure 10. An LCA-join
As an example consider Figure 11. It illustrates the task of finding the closest <title> elements to the <publisher> elements for the data tree of author.xml in Figure 1. The lca is book. The merging process starts with the pointers at the start of each list. The first publisher and title are both descendents (within the range) of the first book, so this publisher is closest to the title. The next publisher however is not within the range of the current lca hence it is not closest to the first title. The LCA-join continues by advancing the lca and child pointers to find the next closest pair.
The LCA-join is of special importance in database management systems. If an XML DBMS can iterate through elements of a particular type, then the closest axis with a non-wildcard node test can be efficiently computed with an LCA-join. The time complexity of an LCA-join is O(n), where n is the number of nodes in a type list. Indexes to map an element type to a list of nodes for that type are commonly available in native XML DBMSs (e.g., Xindice, eXist, and BerkeleyDB-XML provide element type indexes.)
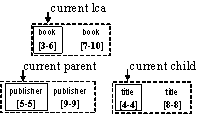
Figure 11. The LCA-join of publisher and title
In this section we turn our attention to the use of the closest axis in practice. To show its wide applicability, we demonstrate how the closest axis can replace directional axes in queries from the first use case in the W3C XML Query Use Cases [16].
We first take a look at two queries from the first use case -"Experiences and Exemplars". For each query, the problem and the solution using the closest axis are shown.
Q1. List books published by Addison-Wesley after 1991, including their year and title.
Solution using the closest axis:
<bib>
{
for $b in doc("http:/bstore1.example.com/bib.xml")->bib->book
where $b->publisher = "Addison-Wesley" and $b->@year > 1991
return
<book year="{ $b->@year }">
{ $b->title }
</book>
}
</bib>
Each of the five closest axes in the above query replaces a child axis in the original query. As we can see, there is no directional axis in the modified query.
Q9. In the document "books.xml", find all section or chapter titles that contain the word "XML", regardless of the level of nesting.
Solution using the closest axis:
<results>
{
for $t in doc("books.xml")/(chapter | section)->title
where contains($t->text(), "XML")
return $t
}
</results>
The closest axes in the above query replace child axes in the original query as well. However, we choose not to replace the descendant-or-self axis with the closest axis. Although it is usually the case that all chapter nodes are of the same distance to the root of a document, it may not always be true. When some chapter nodes are farther away from the root, the closest axis will miss these nodes even though it is the intension that they be selected. In this particular case, doc("books.xml")/chapter is still the best way to properly locate chapter nodes. This example shows that when the descendant-or-self axis is invoked from the document root it functions as a symmetric locator. The expression doc("anyBibDoc.xml")/book is not structure-dependent, and hence is symmetric in effect.
In addition to the queries shown above, we have also inspected other queries in this use case. It turns out that every directional axis in the various use cases can be replaced by the closest axis, with the exception of the descendant axis. This can be explained by the fact that these XPath expressions are all used to located related nodes, and the related nodes are always closest to the context nodes. In this use case, there is no instance of the use of the parent axis; but the closest axis should be effective in replacing it as well should it be used.
Although not present in the entire use cases document, recursive hierarchies can also be problematic. Consider a recursive schema in which all part elements are nested to represent subparts. Located at the leaves in the hierarchy are those atomic parts that have no subparts. In such a hierarchy the expression part->part may or may not give the expected result. This expression returns the immediate subparts while some users may believe all (recursive) subparts should be returned. Again, the descendant-or-self axis should be used to locate all subparts relative to a part.
Some XPath expressions fundamentally depend on a direction and cannot be augmented with a closest axis. An example would be that a query to find the names of all the elements that enclose a book element, a parent axis would be necessary to locate the enclosing element.
By facilitating the symmetric exploitation of hierarchical data, this paper contributes to the following areas. First, it is a means for the integration of XML data, because heterogeneous data can potentially be queried with the same query. Second, it offers a novel (not only syntactically but also semantically) construct to XML query language. A user can effectively query XML data without knowing its specific structure. We review related work in these two areas respectively.
Many research projects have focused on the problem of data integration [2] [5] [6] [10]. The goal of data integration is to combine data from different sources into a single source. From a user's point of view, there is only one source and she can query the data using the schema of that single source. For example, YAT [2] and SilkRoute [5] translate relational data into XML. Query over the underlying relational data is expressed through an XML interface. The heterogeneity considered in these data integration systems largely lies in the form of the data, e.g., relational and XML data. This paper considers XML data only, but with heterogeneous structures.
Data integration systems are usually classified as global-as-view (GAV) and local-as-view (LAV). GAV means that there is a global view, defined as a view over local schemas. In contrast, a LAV approach defines local views in terms of the global schema. Most data integration solutions are GAV, with just a few (for example [10]) being LAV. Since our approach is structure-independent, there is no schema or view visible to a user at all. However, the philosophy of symmetric exploitation can in some sense be regarded as a GAV data integration approach. The notion of a global schema is manifested by the non-directional nature of the closest axis. This schema is essentially a virtual graph. In this graph, each directed edge represents the fact that the destination node is in the closest axis of the source node. None of the (undirected) tree edges needs to be represented in this graph. Such a graph is a special kind of global schema in that the user is not even expected to be aware of it.
Querying hierarchical data is often a non-trivial task. There has been some work on the convenient formulation of queries over XML data. For example, [8] and [12] propose descriptive languages for specifying transformations of XML data. Similar to the closest axis, these languages hide from users much of the procedural specification necessary in a language such as XQuery or XSLT. However, these special-purpose techniques are limited because they still suffer from being structure-dependent. A query might have to be rewritten when the data changes. Our objective to flexibly issue queries independent of the structure is shared by [4] and [9]. [4] presents a semantic search engine for XML. The search relies on an interconnection relationship to decide whether nodes are "semantically related." Two nodes are interconnected if and only if the path between them contains no other node that has the same label as the two nodes. [9] proposes a schema-free XQuery, facilitated by a Meaningful Lowest Common Ancestor Structure (MLCAS) operation. Both the interconnection in [4] and the MLCAS in [9] are similar to the "closest" relationship between nodes in this paper. However, the closest axis is more flexible due to the use of node type. Reasoning solely on node label can lead to more counterintuitive results. With types, a query can be much richer in semantics and can thus produce desirable results more easily.
XPath suffers from a lack of symmetric exploitation in path expressions. Path expressions in XPath are asymmetric because they are enmeshed in the structure of a hierarchy to navigate to desired data. Asymmetric path expressions are brittle and have a tendency to break when the hierarchy evolves or when the expression is applied to a new hierarchy with a different structure. This paper proposes a new axis, which we call the closest axis, that can be used to exploit data symmetrically. The closest axis contains nodes that are closest to the context node, where closeness is measured as the distance from the context node in any direction. Unlike other axes, the closest axis is non-directional. So though the structure of the data may vary, the nodes in the closest axis for a given context node remain closest. We described the syntax and semantics of the closest axis. We also showed how the closest axis can be efficiently implemented for both in-memory and persistent XPath/XQuery evaluation engines. The key to efficient implementation is to use type information to quickly find a path that leads to a closest node. We introduced an LCA-join operation to compute such paths in a persistent implementation. Finally, we showed how some XQuery Use Cases could be rewritten using the closest axis. Though the closest axis does not make the queries significantly shorter, the same queries can be evaluated over heterogeneously structured hierarchies.
Much still remains to be done. Though we have specified the semantics of the closest axis and sketched efficient algorithms to evaluate it, we have yet to implement the axis in a product. We plan to test two implementation strategies using eXist, an open source native XML DBMS. One strategy will utilize a pre-processor to convert non-directional queries into directional queries. This will demonstrate that the closest axis can be implemented as a layer, at low cost. The second strategy will modify the internals of eXist to implement the LCA-join. A benchmark comparison of the two techniques will help to determine the effectiveness of the LCA-join. The LCA-join also has applications in restructuring data, where data is transformed from one hierarchy to another. Another avenue of future work is to define a complete set of non-directional axes. We speculate that there exist other non-directional axes that involve conditions expressed on labels and types. We are also working on a functional query language called PathFree that will entirely eliminate path expressions since the closest axis can be used to locate data and a related technique can restructure data.
[1] V. Christophides, S. Cluet, and J. Sim¨¨on. On wrapping query languages and efficient XML. SIGMOD Record, Volume 29, Issue 2, June 2000, pp. 141-152.
[3] E. F. Codd. A Relational Model of Data for Large Shared Data Banks. Commun. ACM 13(6): 377-387 (1970).
[4] Sara Cohen, Jonathan Mamou, Yaron Kanza, and Yehoshua Sagiv. XSEarch: A Semantic Search Engine for XML. Proceedings of VLDB Conference, Berlin, Germany, 2003, pp. 45-56.
[9] Y. Li, C. Yu, and H. V. Jagadish. Schema-Free XQuery. In Proc. VLDB Conf., Sep. 2004, Toronto, Canada.
[11] P. McBrien, and A. Poulovassilis. A Semantic Approach to Integrating XML and Structured Data Sources. Conference on Advanced Information Systems Engineering, 2000.
[12] T. Pankowski. A High-Level Language for Specifying XML Data Transformations. ADBIS 2004, Springer-Verlag, Lecture Notes in Computer Science 3255, 2004.
[13] World Wide Web Consortium. Document Object Model (DOM). www.w3.org/DOM.
[16] World Wide Web Consortium. XML Query Use Cases. http:/www.w3.org/TR/xquery-use-cases/.
[1] Codd's critique included other arguments such as the critical concept of (physical) data independence that are not germane to this paper.
[2] Due to this simplification, the closest axis will locate elements only. However, the closest axis can be defined for a complete data model as well; in that situation all kinds of nodes can be located.
[3] As an aside, the term path used with precision refers to "the shortest walk" where a walk can contain multiple occurrences of nodes. However, "paths" as used in XPath are in fact "walks", and hence not necessarily the shortest between the source and target nodes. We follow this convention and use "the shortest path" specifically.