Bhushan Mandhani1, Sachindra Joshi2,
Krishna Kummamuru2
1: mandhani@ee.iitb.ac.in, Indian Institute of Technology, Bombay, India
2: {jsachind, kkummamu}@in.ibm.com, IBM India Research Lab, New Delhi, India
Copyright
is held by the author/owner(s).
WWW2003, May 20-24, 2003, Budapest, Hungary.
ACM 1-58113-680-3/03/0005.
The algorithm is a partitional-agglomerative algorithm. The partitioning step involves the identification of dense submatrices so that the respective row sets partition the row set of the complete matrix. The hierarchical agglomerative step involves merging the most ``similar'' submatrices until we are down to the required number of clusters (if we want a flat clustering) or until we have just the single complete matrix left (if we are interested in a hierarchical arrangement of documents). It also generates apt labels for each cluster or hierarchy node. The similarity measure between clusters that we use here for the merging cleverly uses the fact that the clusters here are co-clusters, and is a key point of difference from existing agglomerative algorithms. We will refer to the proposed algorithm as RPSA (Rowset Partitioning and Submatrix Agglomeration). We have compared it as a clustering algorithm with Spherical K-Means and Spectral Graph Partitioning. We have also evaluated some hierarchies generated by the algorithm.
Categories and Subject Descriptors
H.3.3[Information Storage and Retrieval]: Information
Search and Retrieval -- Clustering
General Terms
Algorithms, Performance, Experimentation
The Web has grown from a few hundred thousand pages in early 90s to over 2 billion pages in 2002. IDC reports that over 200 million pages are added every month while at the same time 100 million pages become obsolete. A similar trend has been observed in intranets too. With this explosion of unstructured information, it has become increasingly important to organize the information in a comprehensible and navigable manner. A hierarchical arrangement of documents is very useful in browsing a document collection, as the popularity of the Yahoo, Google and Dmoz web directories has shown. The Dmoz directory has been manually created by about 52 thousand editors. Though manually generated directories are more comprehensible and accurate, they are not always feasible. Therefore, there is a need for tools to automatically arrange documents into labelled hierarchies.
Clustering of documents is an important part of this process. The nodes at each level of the hierarchy can be viewed as a clustering of the documents, with the number of clusters increasing as one goes deeper in the hierarchy. The popular classes of document clustering algorithms are k-means and its variants, hierarchical agglomerative clustering (HAC) methods [1], and more recently, graph partitioning methods [2,3]. For k-means, the best performing similarity measure between documents is the cosine measure between two document vectors [4,5]. HAC algorithms start with singleton documents as clusters, and iteratively merge the two most similar clusters. They differ in their choice of similarity measure between clusters [6,7]. There also exist other methods tailored for clustering search results [8,9]. We will look more closely at clustering literature in section 5.
The model commonly used for documents is the bag-of-words or vector space model. A set of words is chosen from the set of all words in all documents using some criterion. Each document is a vector in the feature space formed by these words. The vector entries can be word frequencies or some other measure. For any moderately sized document set, the number of words runs into a few thousands. Thus document vectors are high-dimensional. Putting these vectors together, we get the document-word matrix which is extremely sparse.
Our proposed algorithm RPSA is a two-step partitional-agglomerative algorithm. The partitioning step involves the creation of ``dense'' submatrices (we define ``dense'' later) so that the respective row sets partition the set of rows of the complete matrix i.e. partition the document set. We will call these submatrices ``leaf clusters'', since they will form the leaf nodes of the hierarchy subsequently created in the agglomerative step. Note that leaf clusters, being submatrices, are document-word co-clusters. The number of these leaf clusters will typically be much larger than the number of clusters desired. Note that though a document can belong to only one leaf cluster, a word can occur in several of them. For the creation of individual leaf clusters, we have used an algorithm which, given a document, creates a leaf cluster containing that document. Thus the partitioning step can be viewed as leader clustering. The second step is hierarchical agglomerative, in which the most similar clusters are successively merged. Our algorithm can be used for both flat clustering, and hierarchical clustering (even though it naturally creates hierarchies even in the former case).
The organisation of this paper is as follows. In the next section, we describe how the document vectors are created, and how we will be evaluating the quality of the clustering, for both the flat and the hierarchical cases. In Section 3, we describe the proposed RPSA algorithm, from the creation of the leaf clusters, to obtaining the final labelled hierarchical clustering. In Section 4, we present our experimental results. For the flat clustering case, we compare our results with those given by bipartite spectral graph partitioning (see [2]), and spherical k-Means. We also compare the labels generated by us with that by the former algorithm. For hierarchical clustering, we have used a couple of data sets downloaded from the dmoz directory. In Section 5, we look at related work, and how RPSA compares with some of the existing algorithms for clustering documents. Finally, we present our conclusions in Section 6.
In the preprocessing, a ``dictionary'' of all the words occurring in the document set is created. Stopwords are then removed. For each word, a count of the number of documents in which it occurs is kept. We then remove words occurring in less than 0.2% of the documents i.e the low-frequency words, and those occurring in more than 20% of the documents i.e the high-frequency words. The remaining words constitute our feature space. They make up the columns of the document-word matrix.
Suppose the feature space consists of n words, and we have d documents. Document i is represented by mi, a vector in the space Rn. The component of this vector corresponding to the j-th word is given by:
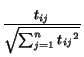log
The following two measures are commonly used to judge cluster quality, given an external partitioning of the documents of the data set into labeled classes. Suppose we have g classes with labels {1, 2,..., g} and k clusters {X1, X2,..., Xk}. We denote by nji the number of members of class i in cluster Xj, and by nj the number of elements making up Xj.
maxi{nji}
pijlog pij
njEj
Though entropy, unlike purity, takes into account the entire confusion matrix i.e all the numbers nji, we believe purity to be a better measure. We explain this with an example. Suppose we represent cluster Xj as a vector in Rg with the i-th component being pij. Suppose g = 4, and we have one cluster given by (0.5, 0.5, 0, 0) and another given by (0.8, 0.1, 0.05, 0.05). The second cluster can be easily identified with the first class, and is clearly the better cluster, and has a higher purity value. However, the entropy of the first cluster is 0.693 while that of the second is 0.708. Entropy identifies the first cluster as the better one! We will be using purity to evaluate our results.
In the original hierarchies, all documents belong to some leaf node. Documents originating at intermediate nodes are not allowed.
The partitioning step of RPSA, as mentioned earlier, creates dense submatrices whose row sets partition the row set of the complete matrix. We will refer to these submatrices as leaf clusters since they are the leaf nodes of the hierarchy subsequently generated. In this section, we will first look at an algorithm that, given a document and a density parameter (explained later), creates a leaf cluster containing that document. We will then see how successive input documents to this algorithm are chosen, and the considerations involved in choosing the density parameter. Finally, we will put these all together to get the complete partitioning step.
We define the density of a matrix of reals as the average value of the entries of the matrix. Given our document-word matrix M, a set R of rows and a set C of columns define a submatrix S of M. We will use d (S) to denote the density of S. The density of a row r over column set C is defined as the average of the entries of r lying in the columns making up C i.e
mrc
We will now consider an algorithm that, given a row i and value
> 1, outputs a submatrix
S of
M
containing the row i and having density approximately
d (M). This algorithm is an
extension of the ping-pong algorithm proposed by [11],
which does the same job for a binary matrix. It is described by the
following steps:
1. Initialize row set
R = {i} and
column set
C to null. Set row threshold tr and column
threshold tc equal to
d (M).
2. Add to
C the columns c whose density over
R is
greater than or equal to tc.
3. Similarly, add to
R
the rows r whose density over
C is greater than or equal
to tr.
4. If
d (S) 
d (M),
Thus the above algorithm, starting with a single row alternately adds columns and rows, stopping after every cycle of addition to check that d (S) is above the threshold. When it can't add new rows or columns, it selectively reduces the row threshold, keeping the column threshold constant. Often the output of this algorithm contains only a few rows, so we selectively reduce the row threshold to encourage the output to have a larger number of rows. In [11], the row and column selection criteria are designed for a {0,1}-matrix and not for a matrix of reals. Further, there is no differentiation between rows and columns.
The first input to the above algorithm is a row number (document). This document can be viewed as the ``leader'' for the subsequently generated leaf cluster. We now see how leader documents are successively chosen to form leaf clusters.
We define the length l (i) of a document i as the sum of the components of the TFIDF vector representing that document. Note that this vector is different from the one representing the document in M, where we have used (unitized-TF)IDF.
tijlog
Documents with relatively large lengths were observed to be better leader documents for the algorithm above. They generally created large and meaningful document clusters, with the cardinality of the associated word clusters typically being 2 to 5 times that of the corresponding document clusters. Documents with the smallest lengths often created skewed clusters having very few rows, and a large number of columns. Such leaf clusters introduce errors in the agglomerative step, and are undesirable.
Suppose at some stage m leaf clusters have been formed. The j-th leaf cluster is the submatrix Sj, defined by the row set Rj and the column set Cj. The leader for the (m + 1)-th cluster has to be chosen from the set L of documents not occurring in any of the m clusters formed so far. For document i in L, we define its membership Mij in cluster j as the density of row i over Cj. It is a measure of the similarity of i with the documents occurring in cluster j. Thus the cumulative membership of i in the clusters formed so far is:
Mij
Mi is a measure of the overall similarity of i with the the existing clusters. As leader, we want a document i in L such that l (i) is relatively large and Mi is as small as possible. Thus from among the length-wise top one-third documents of L, we choose the document i for which Mi is minimum. Thus we have in place the algorithm to choose leader documents.
. The density of the generated leaf cluster
S is approximately
d (M).
Clearly, the larger the value of , the smaller
the size of
S will be and vice versa.
The typical sizes of the generated leaf clusters for
a given were found to be a function of the number of total
documents alone, and independent of the document set involved.
This is not surprising, since in creating the matrix
M we had
first unitized the TF vector, cancelling the effect of varying
document sizes. What this means is that
doesn't need to be tweaked for different data sets.
We experimented with values of varying from 10 to 50. For the
larger values, though the leaf clusters formed have high purity, they
are small, and thus the number of leaf clusters is large.
This not only slows down
the algorithm, but more
importantly, causes errors in the merging step, with the final clusters being
unbalanced in size, and the larger ones having fairly low purity. Low
values of result in slightly lower purity of leaf clusters, but
these leaf clusters are larger, and lesser in number.
This results in
faster running time and, vitally, no errors in the merging. In all
the results shown in this paper, we have used = 20.
The complete partitioning algorithm is as follows:
of the total
document set, find the next leader using the ``choose leader''
algorithm in section 3.1.2 and go back to the above
step. Otherwise proceed.
In our experiments, we used 80% for the value of .
The reason for going upto only 80% of the documents in creating the leaf
clusters is that towards the end we start getting clusters with only a few
documents (we mentioned earlier that this is mostly the case with leader documents
with small lengths), and it becomes more efficient to populate the remaining documents
in the existing clusters as we do in step 4.
Thus, we now have in place a partitioning of the document set into
leaf clusters.
We now discuss the time and space complexity of the partitioning algorithm described above, in terms of the number of nonzero entries z in the d×n document-word matrix M, and the total number of leaf clusters created m. Though m is O(d ) in the worst case, our results later show that m increases very slowly, and not linearly with d. In fact, as d varies from 90 to 3893, m varies from 32 to 117. So we will use m as a parameter in our analysis. Additionally, we use an efficient representation for the sparse matrix M and only store its z nonzero elements.
In step 2, a leaf cluster is created using the algorithm of section 3.1.1.
When creating a leaf cluster, we maintain a list containing for each prospective
row, the sum of its values lying in the current column set of the leaf cluster.
To choose the rows that are to be added, we traverse this list updating the sum
for each prospective row by adding to it its values lying in the columns that
were added to the cluster in the preceding step. This sum is then
divided by the total number of columns in the cluster to get the row density,
and if this exceeds the row threshold, it is added to the cluster. Excluding
the time taken for updating the row sums for the time being, the operation is
constant-time for each prospective row. Thus the time for
adding rows in a single step is
O(d ). Each column is added
to the leaf cluster at most once. When a column is added, the row sums of those
prospective rows have to be updated whose entry in this column is nonzero. Each
such entry requires one addition. Thus, across all column additions, the total time
for updating row sums is
O(z). Similarly, the time for adding columns in
a single step is
O(n), and the total time for updating column sums is
O(z). If we have c addition cycles for creating some leaf cluster,
the time taken for it becomes
O(z + cd + cn). The maximum value of c
was found to be 31 for dmoz300 (a data set of 300 dmoz pages)
and 36 for dmoz1800 (1800 dmoz pages). We can choose to bound c with a constant
, without affecting the performance of the algorithm. Thus, the time for
creating a leaf cluster becomes
O(z). The time for creating m such
leaf clusters is
O(mz).
In step 3, a new leader document is chosen using the method of section 3.1.2. We maintain a list containing the cumulative membership values for each uncovered document. When a new leaf cluster is created, the membership of each uncovered document in this new cluster needs to be computed to update this list. The uncovered documents and the column set of the newly formed leaf cluster make up a submatrix of M. Each nonzero entry of this submatrix results in one addition, giving O(z) additions. The number of divisions and comparisons is O(d ). Thus the time for updating this list, and identifying the next leader is O(z). Moreover, step 3 is repeated (m - 1) times. Thus the total time for choosing leader documents is O(mz). Finally, in step 4, we need to compute, within each of the m leaf clusters, the membership of each uncovered document. We again get for each leaf cluster, a submatrix every nonzero entry of which requires one addition, and every row one division. For m leaf clusters, the total time is again O(mz).
Thus, the time complexity of the complete partitioning algorithm is O(mz). For each leaf cluster, we only need to store the corresponding row numbers and column numbers. The row sets are disjoint, and we don't expect a column to occur in too many leaf clusters. The total space required for the leaf clusters is thus O(d + n). The space needed for the matrix M is O(z). Thus the space complexity is O(z).
The partioning step of RPSA gives a fairly large number of leaf clusters of dense submatrices. This clustering is usually fine grained. The agglomerative step reduces the number of clusters, and makes it coarser. Note, that this step is usually required even if we require a flat clustering. We will first describe this step for flat clustering, and then consider the case when the goal is to obtain a hierarchical clustering.
We successively merge the most similar clusters in a hierarchical agglomerative step, until we are down to the required number of clusters. The similarity measure between two clusters that we use for the merging, cleverly exploits the fact that the clusters are co-clusters, and thus submatrices, and is key to the working of the algorithm.
Recall that the i-th cluster is a submatrix Si defined by the row set Ri and the column set Ci. For clusters i, j, the density of the submatrix formed by the row set Ri and the column set Cj is a measure of how much we can expect to find the words of cluster j in the documents making up cluster i. A similar comment can be made about the submatrix formed by the combination of Rj and Ci. We define the similarity between clusters i, j as the average of all the elements making up these two submatrices.
When we merge clusters i, j, the row set of the obtained cluster is the union of the row sets Ri and Rj, and the column set is, similarly, the union of the corresponding column sets. Thus, using a larger set of small dense submatrices covering all the rows of M, we create a smaller set of larger, sparser submatrices covering all the rows of M. This gives us the final clustering.
The merging process for hierarchy generation is the same as above. The difference is that when we start out, the leaf clusters are all assigned a height 0. Subsequently,
Labels for cluster i come from the column set Ci. We define the degree of description of cluster i for a word w in Ci as the density of column w over the corresponding row set Ri. We expect that the greater this value, the better the description that w provides of the cluster. Thus we can sort the words making up Ci in descending order of their degrees of description. In the results in the next section, the top 7 words have been shown for the clustering experiments, while for hierarchical clustering, the top word for a node has been used as its label.
This hierarchical agglomerative step begins with m leaf clusters, and has complexity quadratic in m. Computing the similarity between two clusters requires taking the average of the elements of two disjoint submatrices of M, and thus takes time O(z). Thus the total time for the agglomerative step is O(m2z). Finally, for each hierarchy node, we store the numbers of the leaf clusters lying in the subtree rooted at the node, and pointers to the children of the node. There are m leaf clusters and O(m) nodes. Thus the extra space required for the agglomerative step is O(m2).
In this section we present the results of our proposed RPSA algorithm for both flat and hierarchical clustering. For the former case, we have compared the results obtained with those given by the Bipartite Spectral Graph Partitioning algorithm and Spherical k-Means.
Dhillon [2] represents the document-word matrix as a bipartite graph with edges running from the set of documents to the set of words. The problem of getting k co-clusters is posed as partitioning the vertices of the graph into k sets so that the sum of the edge weights of edges joining vertices in different sets is minimized. Spherical k-Means (see [5]) uses cosine similarity measure between document vectors. TFIDF vectors are unitized to get the document vectors. Further, the centroid vectors too are unitized. A random number generator was used to choose documents which were made the initial centroids. The results produced by k-means depend on the choice of the initial centroids. Thus for every data set considered, we have run the algorithm 10 times and have shown the average purity, as well as the value coresponding to the best run.
We have used the following three data sets for our experiments:
In addition, we have used a subset of Classic3 made up of 30 documents from each of its 3 sources. We will refer to this 90 document set as 90docs. The idea is to see how the algorithms behave for small data sets. The results of Spectral Graph Partitioning have been taken from [2], and thus are available only for Classic3 and Yahoo_K1.
|
Below we have shown the confusion matrices for RPSA and Graph Partitioning for the Classic3 data set. Note that we can consider Classic3 a ``clean'' data set in the sense that its sources deal with disparate subjects (aerospace, medicine and IR), and the ideal clustering (100% purity clustering) has balanced cluster sizes. All three perform well, with k-Means giving the best results with an average purity of 99.13% (see Table 6), while RPSA gives 98.41%. The labels generated by the two co-clustering algorithms are similar, and give good desciption of the clusters.
|
|
Next, we show the confusion matrices for the Yahoo_K1 data set. Yahoo_K1 is a much more ``noisy'' data set. Moreover, nearly 1900 of the 2340 documents come from just 2 of the 6 categories, namely Health and Entertainment. So, the desired clustering is skewed.
As Table 6 shows, RPSA gives the best results, and is on a par with the best of the 10 k-Means runs with a purity of over 85%. Graph Partitioning gives 79% purity, and is outperformed by the average k-Means run. In fact, as the confusion matrices below show, its performance is actually even worse than the purity comparisons suggest. For RPSA, 5 of the 6 clusters formed are good clusters i.e. they are made up of one dominant category, with negligible or no contributions from the other five. Two of these extract the entire Health and Sports categories respectively. Graph Partitioning on the other hand, gives only 3 good clusters out of 6. Moreover, none of these extract a complete category. Finally, the quality of its labels too can be seen to be inferior to that produced by RPSA, for which not a single label is out of place.
|
|
In NewsGroups data set, there is noise between categories like comp.graphics and pc.hardware,and the number of categories (ten) is relatively large. This is reflected in the low purity values. RPSA outperforms the average k-Means run, but is outperformed by the best k-Means run.
Finally, k-Means is known to perform poorly on small data sets, and this is verified by the results obtained with 90docs. RPSA easily outperforms the best k-Means runs. This poor k-Means performance is because it settles down at an inferior local maxima after 2-3 iterations.
RPSA naturally generates a hierarchy while generating flat clusters. In this subsection, we evaluate the performance of RPSA in creating hierarchies. At different levels of hierarchy, we are interested in evaluating the purity, the number of nodes, and the labels generated for the nodes. Note that for calculating the purity, the nodes of the corresponding level in the original hierarchy are considered the external class labels.
We have used two data sets downloaded from the dmoz web directory.
Arts(600)
Visual Arts(200)
Music(200)
Performing Arts(200)
Business(600)
Management(200)
Accounting(200)
Venture Capital(200)
Health(600)
Alternative(200)
Fitness(200)
Medicine(200)
Arts(150)
Movies(50)
Music(50)
Performing Arts(50)
Business(150)
Management(50)
Accounting(50)
International Business & Trade(50)
|
The hierarchy generated for dmoz1800 is as follows. The numbers in parentheses are the number of documents at a node.
Art(719)
Juggling(171)
Jazz(61)
Dance(210)
Artists(277)
Ventures(502)
Management(115)
Tax(174)
Capital(161)
Leadership(52)
Health(399)
Herbal(75)
Healing(117)
Care(207)
Training(180)
Exercise(54)
Chartered(50)
Partners(76)
|
For dmoz1800, as can be seen from the confusion matrix, nodes ``Art'' and ``Ventures'' respectively extract the ``Arts'' and ``Business'' categories of the original hierarchy. However, the ``Health'' node of the original hierarchy splits into two distinct nodes, ``Health'' and ``Training'', and also has a component in the ``Art'' node. This additional Level 1 node introduces further additional nodes at Level 2, giving 14 Level 2 nodes in all. The Level 1 purity is a bit low. However, the Level 2 purity of over 60% is quite acceptable, considering that the number of class labels is 9, and that we can expect noise between subcategories of the same Level 1 node, for example, between Music and Performing Arts. Finally, the generated taxonomy looks good. Most node labels can be easily mapped to nodes in the original hierarchy. Mapped Level 2 nodes have mapped parents.
The hierarchy generated for dmoz300 is:
Dance(140)
Film(32)
Hip(23)
Folk(85)
Tax(160)
Performance(25)
CPA(63)
Trade(21)
Quality(44)
Strategy(7)
The dmoz300 results show that performance does not degrade for small data sets, as they probably would for a k-Means based hierarchical clustering scheme. One important point to note is that the number of leaf clusters formed is comparable for the two data sets, despite one of them being much larger than the other. Similarly, in the previous subsection, though the number of documents varied from 90 to 3893, the number of leaf clusters formed varies only from 32 to 117. Thus, as mentioned earlier, the leaf cluster sizes scale up with the number of documents, and the total number m of leaf clusters formed grows quite slowly with the data set size. As our analysis of the running time of RPSA showed, this would be important for running RPSA on larger data sets.
The k-means algorithm is an iterative partitioning method. In each iteration, documents are assigned to the cluster with the nearest centroid. Convergence occurs when there is no further movement of points. [4,5] describe the use of k-means for document clustering. They use the cosine measure between document vectors as the document similarity, and call the resulting algorithm spherical k-means. The k-means algorithm is a gradient descent scheme, which looks to minimize the sum of the distances of data points from the centroid of the cluster they belong to. Though it generally performs quite well, it can get stuck at inferior local minima. This is especially the case with small data sets. Its running time is O(zk), where z is the number of nonzero entries in the matrix M (see [4]), and k is the number of desired clusters. We earlier saw the running time of the partitioning step of RPSA to be O(zm). However, k-means runs much faster than the partitioning step of RPSA. This is because the number of times the z entries of M are considered is larger for RPSA. Moreover, the number of leaf clusters m too is much larger than k. K-means is a partitioning algorithm, and does not create hierarchies.
In hierarchical agglomerative clustering (HAC) methods, performance is determined by the choice of similarity measure between clusters. These include:
The only algorithm known to the authors that is similar in spirit to the
partitioning step of RPSA is the Clustering By Committee (CBC) algorithm proposed
in [12]. It has two distinct phases.
In one phase, tight clusters called
committees, are extracted. The algorithm attempts to form as many committees as it
can subject to the condition that the similarity between any two is less than a threshold
. Cosine similarity is used, and the similarity between two committees is the
similarity between their centroids. To create these committees,
for each uncovered document, the algorithm
considers the top-k similar documents for some fixed k, and extracts from it an optimal
cluster. This cluster becomes a committee if its similarity with each of the existing
committees is less than . When this has been done, each uncovered document whose
maximum similarity with a committee centroid is greater than a threshold 
is
assigned to the corresponding cluster. This process is repeated till either no more
committees can be formed or no uncovered documents remain. The leaf clusters created in step
2 of the partitioning step of RPSA (see 3.1.4) are loosely analogous to
the committees of CBC. Our choice of a document having minimum similarity with the existing
leaf clusters as the next leader in step 3 is analogous to the condition that each new
committee's similarity with each of the existing committees is less than . Finally,
in the next phase of CBC, each uncovered document is assigned to the cluster with whose
committee it has greatest similarity. In step 4 of our partitioning step, we similarly
assign each uncovered document to the leaf cluster over whose column set the document has
greatest density.
[2] proposes an algorithm based on spectral graph partitioning. This
algorithm, like the partitioning step of RPSA, is a co-clustering algorithm and
does not use or define any notion of similarity between individual documents.
It models a document collection as a weighted bipartite graph with
each edge running from a document vertex to a word vertex. The edge weight is the
corresponding entry in matrix
M. The cut of vertex sets U, V of the graph
is the sum of weights of edges joining vertices in U and V. The problem of getting
two clusters of the vertex set is posed as the problem of minimizing
the cut of the vertex subsets,
while keeping their sizes balanced. The second eigenvector of the Laplacian matrix
of the graph is a real approximation of the desired partition vector. When the number
of desired clusters k is greater than 2,
log2k
eigenvectors need to be computed.
Grouper [8] is an online clustering interface for web search engine results. Its clustering algorithm is suffix tree clustering (STC) [13], which models a document as a string of words, and not as a vector. Other algorithms include [10], a probabilistic hierarchical clustering algorithm, whose objective function is based on marginal likelihood.
In this paper, we have proposed an algorithm that interprets a dense submatrix of the document-word matrix as a document-word co-cluster. In the first step, we partitioned the row set into a relatively large number of small dense submatrices or leaf clusters. Then, we merged them to get a smaller number of larger, sparser submatrices. We have also defined a criterion to choose labels from the word cluster of a co-cluster.
In flat clustering, though their performances for the Classic3 data set were similar, for the noisier Yahoo_K1 data set, RPSA outperforms Spectral Graph Partitioning, with respect to both cluster purity and label quality. In fact, in all but one case, it is comparable with or better than the best k-means run. Moreover, its performance does not degrade on small data sets. As a hierarchical clustering algorithm, RPSA does a good job in the hierarchy creation and node labeling. As we go down in a hierarchy, the number of nodes shoots up, and it becomes difficult to obtain high purity values. RPSA was found to give acceptable purity values at Level 2 of the two dmoz data sets.
The main application of RPSA would be for browsing large, unknown document collections. Another would be in organising search results. Finally, we can exploit the fact that ours is a co-clustering algorithm for feature selection in unsupervised learning. Every document belongs to a document cluster, and has an associated word cluster, which can be used as its set of features.
This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.62)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -no_math -html_version 4.0,math -split +0 -link 1 -show_section_numbers -local_icons -antialias_text rpsa.tex
The translation was initiated by on 2003-04-11