Dynamic Maintenance of Web Indexes Using Landmarks

Lipyeow Lim 1

Duke University
Durham, NC 27708-0129, USA.

Min Wang

IBM T. J. Watson Research Ctr.
Hawthorne, NY 10532, USA.

Sriram Padmanabhan

IBM T. J. Watson Research Ctr.
Hawthorne, NY 10532, USA.

Jeffrey Scott Vitter 2

Purdue University
West Lafayette, IN 47907, USA.

Ramesh Agarwal

IBM Almaden Research Ctr.
San Jose, CA 95120-6099, USA.

Abstract

Recent work on incremental crawling has enabled the indexed document collection of a search engine to be more synchronized with the changing World Wide Web. However, this synchronized collection is not immediately searchable, because the keyword index is rebuilt from scratch less frequently than the collection can be refreshed. An inverted index is usually used to index documents crawled from the web. Complete index rebuild at high frequency is expensive. Previous work on incremental inverted index updates have been restricted to adding and removing documents. Updating the inverted index for previously indexed documents that have changed has not been addressed.

In this paper, we propose an efficient method to update the inverted index for previously indexed documents whose contents have changed. Our method uses the idea of landmarks together with the diff algorithm to significantly reduce the number of postings in the inverted index that need to be updated. Our experiments verify that our landmark-diff method results in significant savings in the number of update operations on the inverted index.

1 Introduction

The inverted index is the indexing technique of choice for web documents. Search engines use an inverted index for HTML documents [18], and DBMSs use it to support containment queries in XML documents [14, 24]. An inverted index is a collection of inverted lists, where each list is associated with a particular word. An inverted list for a given word is a collection of document IDs of those documents that contain the word. If the position of a word occurrence in a document is needed, each document ID entry in the inverted list also contains a list of location IDs. Positional information of words is needed for proximity queries and query result ranking [18]. Omitting positional information in the inverted index is therefore a serious limitation. Positional information is usually stored in the form of location IDs. The location ID of a word is the position in the document where the word occurs. An entry in an inverted file is also called a posting; it encodes the information <word_id, doc_id, loc_id> .

Since web documents change frequently, keeping inverted indexes up-to-date is crucial in making the most recently crawled web documents searchable. A crawler is a program that collects web documents to be indexed. Cho and Garcia-Molina [7] have shown that an in-place, incremental crawler can improve the freshness of the inverted index. However, the index rebuild method commonly used for updating the inverted index cannot take advantage of an incremental crawler, because the updated documents crawled in between rebuilds are not searchable until the next index rebuild.

In this paper we study the problem of keeping inverted indexes up-to-date. We first describe two general approaches and then show how our proposed landmark-diff method addresses the deficiencies in these two approaches.

The first approach is to rebuild the index more frequently. As the interval between rebuilds gets smaller, the magnitude of change between the two snapshots of the indexed collection also becomes smaller [7]. A large portion of the inverted index will remain unchanged, and a large portion of the work done by the rebuild is redundant.

The second approach is to store the updates in between rebuilds in a searchable update log. This is similar to the `stop-press' technique [23] used to store the postings of documents that need to be inserted into the indexed collection. Each entry in this update log is a delete or insert posting operation. Query processing will need to search both the inverted index and the update log, and merge the results of both. If positional information is stored in each posting, which is often the case, the size of the update log will be prohibitively large.

Frequent rebuild is inefficient because it rebuilds portions of the index that did not change. The update log is unsatisfactory because it is too large and affects query response time. A better way of updating the inverted index is needed. An update method has to handle three types of changes: (1) documents that no longer exist (henceforth ``deleted documents''); (2) new documents (henceforth ``inserted documents''); (3) common documents that have changed. In order not to re-index common documents that did not change, an incremental update method is needed. Previous work on incremental inverted index updates has addressed changes due to inserted documents [11, 5,19] and deleted documents [9, 8,19]. Changes due to common documents that have changed have not been addressed.

In this paper, we propose the landmark-diff update method that addresses the problem of updating the inverted index in response to changes in the common documents. We show that solving this particular problem results in very efficient solutions to the more general index update problem.

Our landmark-diff method is based on the diff of the old and updated documents, and the encoding of positional information using landmarks in a document. Positional information is stored as a landmark-offset pair and the position of a landmark in a document is stored in a separate landmark directory for each document. The landmark encoding scheme reduces the number of inverted index update operations obtained from the diff output, because postings using landmarks are more ``shift-invariant''.

1.1 Our Contributions

First, our method addresses how to incrementally update the inverted index for previously indexed documents whose contents have changed. This problem has not been addressed before.

Second, our method uses a landmark-offset pair to represent positional information. This representation has three advantages: it renders postings more ``shift-invariant'', it does not increase the index size, and it does not affect query processing (Section 2.4). The mapping of a landmark to its position in a document is maintained in a landmark directory. A landmark directory is very small compared with the size of the document and hence does not measurably affect query response time. We show that this landmark-offset representation significantly reduces the number of update operations on the inverted index when used with the diff approach.

Third, our landmark-diff method is a general method that can be applied in a variety of ways. It can also be used to optimize many existing methods. Some possible applications are discussed in Section 2.3.

Fourth, we show that our landmark-diff method is three times faster than the forward index method (described in Section 2.1) in updating the inverted index for common documents that have changed. We also show how our landmark-diff method can be used in the partial rebuild method (described in Section 2.3) to solve the more general inverted index update problem where all three types of changes (deleted, inserted, and common documents) are addressed. The partial rebuild method is twice as fast as a complete rebuild. The partial rebuild method uses an array-based implementation of the inverted index, because the set of inserted documents is of the same magnitude as the set of common documents. As the update frequency increases, the number of inserted documents and the number of update operations for the common documents will be very small. Using our landmark-diff update method on a B-tree implementation of the inverted index will result in an even more dramatic speedup.

In the rest of this section we discuss related work and preliminaries. In Section 2 we describe current indexing techniques and our landmark-diff method. In Section 4 we provide empirical validation.

1.2 Relation with Prior Work

Information retrieval using inverted indexes is a well studied field [2, 23]. Although most of the update techniques generalize to keyword searches in web documents (HTML and XML files), several assumptions made by those techniques need to be re-examined. First, web documents are more dynamic than the text document collections assumed by those techniques. Most of the past work on incremental updates of inverted indexes [5, 19,10, 2,23] deal with additions of new documents to a collection of static documents. Static documents are existing documents in the collection whose contents do not change over time. The problem that we try to solve in this paper deals with existing documents whose contents do change over time.

Second, previous work assumes that the inverted index resides on disk or in some persistent storage and try to optimize the propagation of in-memory update posting operations to the inverted file in persistent storage [19, 5,9, 8]. Current search engines keep a large portion of the inverted index in memory3, especially the most frequently queried portions of the inverted index. Even though the indexed collection is growing, we have three reasons to believe that a large portion of the inverted index will still be kept in memory: (1) query volume is increasing and there is a demand for increasing query processing speed; (2) the cost of memory chips is relatively low and still decreasing; (3) the ease of scaling with parallel architecture. Not only does the inverted index in persistent storage need to be updated, but the portion of the inverted index in memory needs to be updated as well. The update method we propose in this paper addresses the problem of updating the inverted index as a data structure independent of whether it resides in memory or on disk. In many cases, our method could be used in conjunction with existing techniques to speedup the propagation of updates to the off-memory inverted index. Several of these existing techniques will be described in greater detail next.

For append-only inverted index updates, Tomasic et al. [19] proposed a dual inverted list data structure: the in-memory short list and the disk-based long list. New postings are appended to their corresponding short lists and the longest short list is migrated into a long list when the storage area for the short lists is full. Brown et al. [5] proposed another incremental append strategy that uses overflow `buckets' to handle the new postings in the relevant inverted lists. These overflow buckets are chained together and have sizes that are powers of 2. Both [19] and [5] deal with append-only incremental updates and assume that a document never changes once indexed. Our method tackles the complementary problem of updating previously indexed documents that have changed.

Clarke et al. [9, 8] addressed the deficiency of these append-only inverted index techniques and proposed a block-based organization of the inverted index that supports deletion of documents as well. The entire document collection is concatenated into a long sequence of words. Positional information of a posting is reckoned from the beginning of the document collection (as opposed to the beginning of each document). Hence, even though Clarke's inverted index supports updates at the postings level, it does not solve the problem of small changes in documents causing a shift in the positional information of many postings unrelated to the change. In fact, the positional shift problem is exacerbated by the use of absolute positional information reckoned from the beginning of the collection.

A technique related to landmarks, called ``chunking'', was used by Glimpse [16] in another context related to text indexing. The idea is to reduce the granularity of the pointers in the inverted lists so that the pointers point to pages rather than to individual words in the text. Given the page a word appears on, the actual occurrence can be found by fast sequential search, such as Knuth-Morris-Pratt [ 12] or Boyer-Moore [ 3]. In our work, landmarks are used to provide relative addressing. When the offsets remain constant, only the landmark locations in a landmark directory need to be updated.

1.3 Preliminaries: Web Data

A sample S(n) is the set of web documents corresponding to one snapshot of the web at a particular time n. The sampling interval between two samples is the time between the two consecutive samples. Consider two consecutive samples S(n) and S(n + 1). Any document can only belong to one of the following partitions: common documents S(n)$ \cap$S(n + 1), deleted documents S(n)-S(n + 1), and inserted documents S(n + 1)-S(n). Three operations are needed to update the index of S(n) so that it reflects S(n + 1):

  1. postings corresponding to the deleted documents need to be removed from the current index,
  2. postings corresponding to the inserted documents need to be inserted to into the index, and
  3. postings corresponding to the common documents that have changed need to be updated in the index.

Data analysis4from [15] showed that (1) common documents represents at least 50% of the currently indexed collection; (2) of the common documents, most of the changes are small; (3) most of the changes are spatially localized within the document. The update method using landmarks that we propose is a scheme that exploits these properties.

2 Updating Inverted Indexes

2.1 Current Methods

Before we describe our method in detail, we briefly describe some existing data structures and update algorithms. We discuss three naive methods: the index rebuild, document update, and forward index methods. The forward index method represents the best of these naive methods and it will be used as a benchmark in our experiments.

Index Rebuild. In this method, the old inverted index is discarded, and the entire updated document collection is scanned, sorted and a new inverted index is constructed (see [23] for details). A complete index rebuild consumes a considerable amount of resources. The entire document collection has to be crawled at periodic intervals and every word in the collection has to be scanned to construct the inverted file. Distributed rebuilding technique such as [17] parallelizes (and pipelines) the process, but does not eliminate the need of scanning every word in every document. Scanning and re-indexing the words in documents that did not change is very wasteful. Rebuilding is preferable only if (1) there are very few common documents (|S(n)$ \cap$S(n + 1)| is small), or (2) the set of common word occurrences is small, i.e., a large portion of each updated document has changed. Data analysis in [15] has showed that this is not the case in practice: The set of common documents is usually large, and the changes to the common documents are small and clustered. Consequently, a large portion of the inverted index can remain unchanged and rebuilding the large portion that is unchanged is a waste of resources.

Document Delete and Insert. One improvement over index rebuild is to process only documents that have changed. Using this method web documents can be crawled at different sampling intervals depending on their rate of change. Incremental crawling has been addressed in [6, 4,13, 7] and optimal crawling frequency is discussed in [6, 4,13]. For each document that has changed, we delete all the postings for the old version of that document in the inverted index and insert the postings of the new document. The worst case number of postings deleted and inserted is O(m + n), where m and n are the number of words in the old and new version of the document, respectively. This inverted index update method is efficient for documents that have a big percentage of their contents changed. Most web documents, however, have small content changes between two consecutive crawlings [15].

Forward Index Update. Forward indexes were first mentioned in Page and Brin's paper describing the Google search engine [18]. For each document, a forward index stores the words that occur in that document and the positions of each occurrence (see Figure 1).

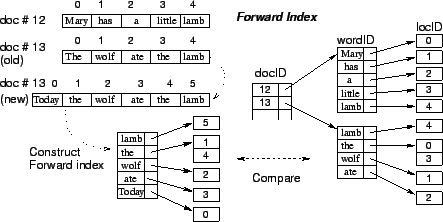
\begin{figure}\centering \epsfig{file=fig/ufwdindex.eps, width=.8\textwidth}\end{figure}

Figure 1: An example of a forward index. For the new version of the document #13 (with ``Today'' inserted to the beginning), a forward index representation is constructed. This forward index is then compared with the forward index of the old version stored by the system. Note how the location IDs of the words changes.

It differs from the inverted index in that it stores the same tuples <word_id, doc_id, loc_id> sorted first by doc_id, then by word_id and loc_id. It is primarily used as an auxiliary data structure to speedup inverted index construction. It is not clear whether it is used for index updates, but we deduce that it can be used for index updates as described next.

Given the forward index representation of the old and new document, we can generate a list of postings operations (insert posting and delete posting) that will transform the forward index of the old document to that of the new document. Since these postings or tuples are the same tuples that are stored in the inverted index, we can use them to update the inverted index. See Figure 2 for the data flow diagram for this process. Applying the procedure for each common document that has changed will update the inverted index.

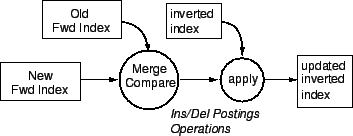
\begin{figure}\centering \epsfig{file=fig/fwdidfd.eps, height=1.2in}\end{figure}

Figure 2: Updating an inverted index using forward indexes.

The forward index method requires an additional forward index to be stored for each document. Each forward index of a document requires as much space as each document itself. The advantage of using the forward index is that when the content change occurs near the end of the document, the postings corresponding to the words before the position of that change need not to be deleted and re-inserted. However, in the worst case, the number of postings deleted and inserted is $ \Theta$(m + n). Even if the difference between the two document is small, the number of posting operations can still be $ \Omega$(m + n). For example, an insertion of one word to the beginning of the old document will shift all subsequent loc_ids by one and hence all the postings will have to change.

2.2 Our Landmark-diff Update Method

In this paper, we propose the landmark-diff update method. The landmark-diff method encodes the position of words using landmarks in a document and performs a diff of the old and new document to get an edit transcript. An edit transcript is a list of operations that when applied to an old version of a document will transform it to the new version. The landmarks encoding scheme allow us to translate the edit transcript for the document into a compact list of update operations on the inverted index. The landmark encoding scheme achieves the following desirable property: the location information of each posting is shift invariant, i.e., an insertion of one word to the beginning of a document will not shift the actual position of all subsequent words. Together with the translation of the document diff output, our method achieves another desirable property: The number of update operations on the inverted index (the number of postings deleted and inserted) is independent of the document size, and depends on the size of the content change only. Since most content changes are small, this property is highly desirable.

We first introduce the landmark encoding scheme and then describe the landmark-diff update procedure.

Landmarks. The purpose of landmarks is to minimize the changes to the location IDs stored in the inverted index when documents change. The idea is for a location ID to take reference from a landmark within the document instead of from the beginning of the document. Each location ID of a word is then encoded as a <landmark_id , offset> pair. The offset in a <landmark_id , offset> pair is the position of the word occurrence relative to the landmark with the specified ID in the document. A document can contain many landmarks. Each landmark has an ID and acts as a reference point for the words between itself and the next landmark. How landmarks are chosen is discussed in Section 2.5.

Putting landmarks in a document can be thought of as partitioning a document into blocks, where the beginning of each block corresponds to a landmark and the location of every word in a block is encoded as an offset from the beginning of that block. In this paper, the term block denotes the words between consecutive landmarks. Each landmark corresponds to a block and vice versa. Figure 3 shows an inverted index with landmarks.

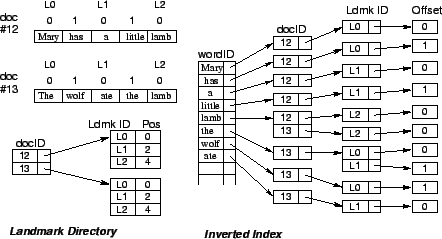
\begin{figure}\centering \epsfig{file=fig/ldmkinvindex.eps,width=.8\textwidth}\end{figure}

Figure 3: An inverted index with landmarks.

The landmark encoding does not increase the index size. Suppose k bits are allocated for each loc_id in the inverted index. The corresponding <landmark_id , offset> pair can be viewed as using the most significant b bits of the original loc_id as the landmark ID and the least significant k-b bits as the offset.

To recover the actual position of a word given the landmark ID and offset pair, the actual position of each landmark in a document must be stored in a landmark directory. For brevity, analytical performance evaluation and implementation issues for the landmark directory are defered to the full paper.

Update Procedure Using Landmarks. Our landmark-diff update method is based on the idea of edit transcripts. To update an inverted index, we can obtain the edit transcript (``diff output'') of the old and the new inverted index and apply it to the old inverted index. The landmark encoding scheme allows us to construct this edit transcript for the inverted index using the edit transcript of each document, without increasing the number of delete or insert posting operations per document to $ \Omega$(m + n), where m and n are the number of words in the old and new version of a document. The update procedure is outlined in the data flow diagram in Figure 4.

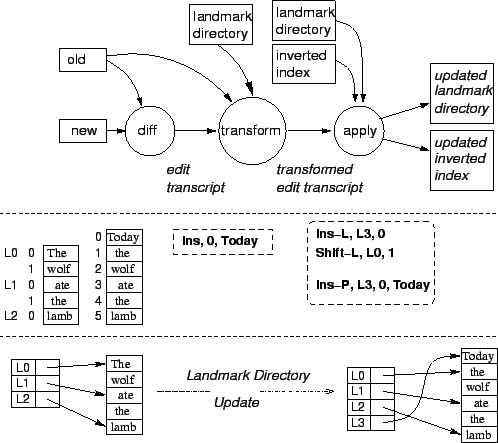
\begin{figure}\centering \epsfig{file=fig/ldmkdfd2.eps, width=.9\textwidth}\end{figure}

Figure 4: The inverted index update method using landmarks. The top diagram shows the data flow; the middle diagram shows what the edit transcripts look like with an example; the bottom diagram show how the landmark directory is updated. The landmark directory is represented here conceptually as a table.

For each document that has changed, we obtain the edit transcript for updating that document using a diff procedure. The diff output is then transformed into corresponding entries in the edit transcript for the inverted index using landmark information. Recall that the edit transcript for the inverted index is a list of update operations on the inverted index. This list of update operations can then be applied to the inverted index to update it. All the procedures before the apply step use only the old document, its landmark directory, and the new version of the document; therefore these procedures lend themselves to parallel processing.

Since words are inserted and/or deleted from the blocks within a document during an update, the absolute position of landmarks within that document may change as well. The landmark directory will therefore have to be updated. Updating a landmark directory can be done very efficiently in a single sequential scan through the landmark directory data structure. This process is linear in the size of the landmark directory and the number of landmarks deleted and inserted. The overhead incurred for storing and maintaining landmark directories is insignificant compared to the savings gained in the number of inverted update operations and in the update time as shown by our empirical evaluations in Section 4. Further analysis of landmark directories will be given in the full paper.

2.3 Some Application Scenarios

We describe three example scenarios to illustrate how our landmark-diff method can be applied. In all three cases, the goal is to update the inverted index given a new sample of the web.

Update Log. If the inverted index is maintained using an update log (similar to ``stop-press'') in between complete index rebuilds, our landmark-diff method can reduce the size of the update log. The naive update log corresponds to the list of inverted index update operations generated by the forward index update method (Section 2.1). Our landmark-diff update method can be used to significantly reduce the size of this update log and thus the query processing time.

Partial Rebuild. In contrast to a complete rebuild, a partial rebuild avoids re-indexing the common documents that did not change. Suppose that the inverted index is stored as a sorted array A_index of postings, the doc_ids of the deleted documents are stored in a bitmap B_deleted, and the postings of the inserted documents are stored in a sorted array A_inserted (stop-press). The landmark-diff method can be used to maintain a reduced-size sorted update log A_update for the common documents. The inverted index can then be updated in a single merging pass of three sorted arrays (A_index, A_update and A_inserted) (checking B_deleted for deletes). Our experiments described in Section 4.4 show that partial rebuild can be twice as fast as complete rebuild.

Distributed Index Update. Suppose the document collection is partitioned among M machines and indexed independently. At each update, each machine updates its index using a bitmap for the deleted documents and the landmark-diff method for the common documents. Inserted documents are always processed at a free machine that builds an index for them. When no free machines are available, the indexes at two machines whose indexes have become too small are merged and one machine is freed.

2.4 Query Processing with Landmarks

In this section we describe how query processing for several types of queries can be done using an inverted index with landmarks. The overhead incurred in computing the actual position of a landmark for some query types depends on the specific implementations of the landmark directory, and we defer that analysis to the full paper.

Single keyword queries. To find which documents contain a particular keyword, we look up the inverted index entry for that keyword and return the list of document IDs. If positional information is required (e.g., single keyword queries with positional constraints), the actual word positions can be computed from each <keyword, doc_id, landmark_id , offset> tuple returned from the inverted index. To do that we retrieve the actual positions of the landmark IDs from the landmark directory of each document containing that keyword.

Phrase queries. Some search engines have assigned unique word IDs for common phrases as well and indexed them as if they were single words. Using that approach, a query using a common phrase is the same as a single keyword query.

We consider the other case, when the phrase is not mapped to a word ID. Without loss of generality we consider a phrase query of two keywords. The 2-keyword phrase query is first processed as two separate single keyword queries. If positional information is required (e.g., a phrase query with constraints on where the phrase occurs in the document), then the actual word position is computed for each keyword in the same way as for processing single keyword queries. The position information is then used to filter out documents where the two keywords are not adjacent to each other.

If positional information is not required, we can perform the filtering of the non-adjacent occurrence tuples without accessing the landmark directory at all. We store an additional field in the last word occurrence of every block. The additional field stores the ID of the next landmark. Given a phrase query (key1 key2), we obtain the tuples corresponding to the occurrence of each keyword independently. Tuples with the same document ID are grouped together and we determine if two tuples, <key1, doc_id, landmark_id 1, offset1> and <key2, doc_id, landmark_id 2, offset1> for keywords key1 and key2, respectively, form a phrase as follows: If landmark_id 1 is equal to landmark_id 2 and the difference between offset1 and offset1 is 1, they form a phrase. If landmark_id 1 is not equal to landmark_id 2, we check if the offset for key2 is zero. If it is zero and the tuple for key1 has the additional next landmark field that is equal to landmark_id 2, then they form a phrase. Otherwise the two tuples do not form a phrase.

Approximate nearness queries. If fine grain positional information is not needed, the inverted index can just store the landmark IDs without the offsets. This results in significant time and space savings, since only the landmark IDs need to be updated. Each posting in the inverted index will then store the information <word_id, doc_id, landmark_id > . Each landmark ID encodes an approximate position with a bounded error (which is the block size).

AND-queries. For a query that contains conjunctions of multiple keywords, we retrieve the tuples for each keyword as if they are single keyword queries. These tuples are then filtered with the tuples corresponding to the most selective keyword5. The detailed analysis is defered to the full paper.

2.5 Landmarking Policy

A landmarking policy describes how landmarks are chosen in a document. Example landmarking policies are fixed size partitioning, HTML/XML tags, metadata, and semantic structure of document.

Fixed size partitioning. The simplest landmarking policy is fixed size partitioning: the size of every block is fixed at the time of index construction. When a piece of text is inserted, the landmarking policy has to decide whether to make a block bigger or to split a block. Fragmentation could occur after a large number of updates, and defragmentation or index rebuild should be performed when update performance degrades. Since content changes in the updated documents are small, fragmentation would not occur frequently.

In fixed size landmarking, the landmarks are not inherent in the structure of the document. A brute-force diff is required to generate the edit transcript that is used to figure out how the landmarks shift between the two versions of a document.

HTML/XML tags. HTML tags such as the paragraph tag (<p>) can also be used as landmarks. In contrast to the fixed size policy, the landmarks in this case are inherent in the document. A more efficient, block-based, approximate diff procedure could be used instead of the brute force diff. For example, we could hash each block of the original and new versions and do the diff on the substantially smaller sequence of hashed values.

How should we choose tags for landmarking? Linear-time heuristics can be used to check which tags (or combinations of tags) that are suitable as landmarks. A brief description of the landmarking tags being used will then be stored together with the landmark directory. XML tags can be used in a similar way.

4 Experimental Evaluation

In this section we describe the experiments used to evaluate our landmark-diff method. We measure the number of inverted index update operations generated by our method and compare it with that of the forward index method. We also measure the time to generate those operations, the time to apply those operations to the inverted index, and the time to bring the inverted index up-to-date.

Through our experiments, we answer four important questions about the performance of our landmark-diff method:

  1. Does the landmark-diff method significantly reduce the number of edit operations on the inverted index compared to other methods (e.g., forward index method)?
  2. Does the reduction in the number of inverted index update operations actually translate to savings in real execution time when applying these operations?
  3. Does generating update operations using the landmark-diff method require more time than other methods?
  4. Does the landmark-diff method provide a more efficient solution for the general inverted index maintenance problem than complete rebuild method, especially when the change between two consecutive samples is large?

Our Implementation. We implemented our text indexing system in C. Two implementations of the inverted index have been used: the binary tree where each node corresponds to a posting, and a b-way search structure implicitly represented by a linear array of postings. We discuss a B-tree representation in Section 4.5 which will take better advantage of our landmark-diff method when updates are very frequent and therefore very small in magnitude. Linear arrays are used for the landmark directory and forward indexes, since these are small data structures. Besides the landmark-diff update method, the forward index update method is also implemented for comparison.

Landmarking Policy and Block Size. Fixed size partitioning is used to choose landmarks. Intuitively, the square root of the average document size is a good block size6. For the experiments we present, a default block size of 32 words is chosen since the average document size is roughly 1000 words. We also measured the minimum number of inverted index edit operations required for different block sizes (using data set I described below) and verified that as the block size gets smaller the number of operations decreases at the expense of increasing landmark directory size and number of landmark directory update operations.

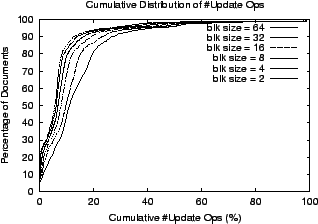
\begin{figure}\centering {\epsfig{file=data/u.cdf.eps, width=.6\textwidth}}\end{figure}

Figure 6: Cumulative distribution of documents with respect to the number of inverted index update operations for different block sizes.

Figure 6 shows the distribution of the documents with respect to the number of inverted index edit operations normalized by the sum of the sizes of the old and new documents. We do not use extremely small block sizes, because as block size gets smaller, the size of each landmark directory grows larger and the cost of manipulating the landmark directory increases as well.

Performance Measures. We evaluate the performance of our landmark method using four measures:

  1. the number of inverted index update operations (Table 2),
  2. the time to perform those operations (Table 3),
  3. the time to generate those operations (Table 4), and
  4. the time to bring the inverted index up-to-date using the partial rebuild method (Table 5).

An edit operation is defined to be a delete posting or insert posting operation. The number of edit operations on the inverted index is a natural performance measure, since the goal of a good update method is to reduce the number of edit operations on the inverted index. Moreover, unlike the execution time, the number of edit operations depends neither on the implementation of the system nor on the hardware architecture. The number of edit operations is therefore a good measure of update performance across different search engine architectures and implementations.

Data Set. Two sets of data are crawled from the web. Data Set I consists of two samples of the web crawled from 100 seed web sites. The time between the start of the two web crawls is 71 hours and the recursion depth is limited to 5 levels. The first sample has 63,336 documents and the second has 64,639 documents with 37,641 documents common to both. Each sample contains about 1.5 GB worth of HTML files. Data Set II consists of 6 samples of the web crawled from 5 seed web sites (www.cnn.com, www.ebay.com, www.yahoo.com, espn.go.com, and www.duke.edu). The sampling interval is 12 hours and the recursion depth is 5 levels. Note that 4 out of the 5 listed web sites have content that is dynamic and fast changing.

Document Preprocessing. Every HTML file is preprocessed into a canonical form by stripping off HTML tags, scripting code, JAVA code, and extra white space. Every letter in each word is capitalized so that different capitalizations do not result in different word IDs. If the canonical form of a file has less than 10 words, it is discarded.

4.1 Number of Update Operations

We investigate the number of the inverted index update operations generated by the forward index method and our landmark-diff method on two data sets. Fixed size landmarking policy is used with a block size of 32 words.

Data $ \mathcal{C}$(docs) $ \Delta $ $ \mathcal{C}$(docs) Fwd. Index Landmark
I 37,641 10,743 10,501,047 3,360,292
IIa 2,026 1,209 1,109,745 330,695
IIb 5,456 1,226 1,566,239 350,802
IIc 5,335 3,096 1,855,618 534,088
IId 5,394 1,278 1,426,163 378,661
IIe 5,783 1,605 1,762,018 539,594

Table 2: The number of update operations generated by the update methods in our experiments. The symbol $ \mathcal{C}$ denotes the number of common documents (|S(n)$ \cap$S(n + 1)|) and the symbol $ \Delta $$ \mathcal{C}$ denotes the portion of $ \mathcal{C}$ that has changed.

Our results in Table 2 show that the landmark-diff method generates significantly less update operations on the inverted index than the forward index method (which represents the best of the naive methods). The performance of the landmark-diff update method is consistent over a broad range of web sites including web sites with fast changing content. We indicate in Section 4.5 that this measure will mirror real-world performance when updates are frequent.

4.2 Update Time

Do these reductions in the number of inverted index update operations actually translate to savings in the time to apply these operations? We measure the execution time for applying the update operations generated by the forward index method and the landmark-diff method to a binary tree implementation of the inverted index for data set I. The experiment is performed on a Sun Blade-1000 computer running SunOS 5.8 with 4 GB of ra

Method |S(n)| No. Update Ops. Time (s)
Fwd. Index 63,336 10,501,047 28.3
Landmark 63,336 3,360,292 9.2

Table 3: Time required to apply the update operations on a binary tree implementation of the inverted index. The symbol |S(n)| denote the number of documents in the index and corresponds to the index size.

We measure the elapsed time for updating the inverted index given the inverted index and the edit operations generated by the two update methods. Our results as summarized in Table 3 show that a reduction in the number of update operations does translate to a proportional reduction in the time required to update the inverted index. Updating the landmark directory requires only one linear pass and is done at the same time as generating the update operations (see Section 4.3).

4.3 Time for Generating Update Operations

Does generating update operations using the landmark-diff method require prohibitively more time than other more naive methods? We measured the time used to generate the update operations for data set I using the same configuration as in Section 4.2.

  Generation Time (s)
Method No. Update Ops $ \mathcal{C}$ $ \Delta $$ \mathcal{C}$
Fwd. Index 10,501,047 148.9 18.9
Landmark 3,360,292 17.5 7.5

Table 4: The time (in seconds) required to generate the inverted index update operations for the landmark-diff method and the forward index method. The $ \mathcal{C}$ column gives the required time if all the common files (37,641) have to be checked and processed. The $ \Delta $$ \mathcal{C}$ column gives the required time, if incremental crawling is used and the system know a priori whether a common file has been modified since the last crawl.

Table 4 summarizes our results. Recall that the forward index requires reading two files, the old and the new document, and creating forward indexes for the two files. The landmark-diff method requires reading the two files in order to perform a diff and in order to generate update operations for postings that have shifted due to edits. The time of the diff operation is remarkably fast compared to the construction of the forward indexes. Even if the landmark directory is stored on disk, the additional time required to read it into memory is still small compared with reading a document, since it is much smaller in size.

We also investigated how the landmark size affects the time required to generate the update operations for the common documents (data set I) that have changed (see Figure 7). Smaller landmark size results in less update operations (since changes in the document are more localized) and therefore less processing time to generate those update operations. However, extremely small landmark size (a size of 4 words in this case) produces big landmark directories that require more time to manipulate.

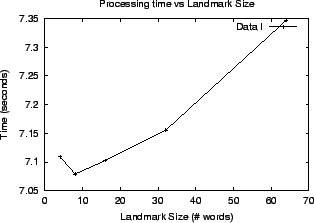
\begin{figure}\centering \epsfig{file=data/blksize.eps, width=.6\textwidth}\end{figure}

Figure 7: Landmark size versus time to generate update operations for common documents that have changed.

4.4 Partial Rebuild Using Landmark-diff

For changes in common documents, we have shown that the landmark-diff method results in a speedup factor of 2 over the forward index method. One may suspect that the speedup is only for the cases when the changes between the two consecutive samples are small, and when the changes are large, complete rebuild may perform better. We now show how the landmark-diff method can be used with the partial rebuild method (see Section 2.3) to solve the general inverted index update problem more efficiently than the complete rebuild method.

The inverted index is implemented as a sorted array of postings residing on disk (searching can be accomplished using an implicit complete B-way tree similar to a binary heap implemented as an array). Deleted document IDs are stored in a bit map in memory. Inserted documents are read and their postings are stored in a sorted array in memory. The update operations for the common documents are generated using our landmark-diff method, sorted, and stored on disk. The old inverted index, the bit map, the array of new postings, and the sorted update operations are merged (in a fashion similar to mergesort) into an updated inverted index on disk (see Figure 8).

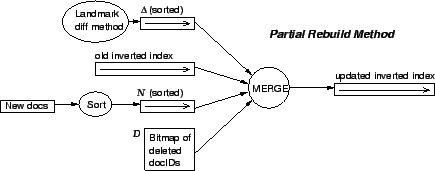
\begin{figure}\centering \epsfig{file=fig/prebuild, width=.8\textwidth}\end{figure}

Figure 8: The schematic diagram for the partial rebuild method. Our landmark-diff method produces a list of update operations $ \Delta $ which is then sorted. The new documents are processed into a sorted list of postings $ \mathcal{D}$ to be inserted. The doc_ids of the deleted documents are stored in a bitmap. These three data structures are merged with the old inverted index in a linear pass.

This partial rebuild using landmark-diff method is applied on data set I and the results are summarized in Table 5.

  No. of docs No. of postings
$ \mathcal{D}$ 25,695 -
$ \mathcal{C}$ 37,641 58,575,596
$\Delta\ensuremath{\mathcal{C}}$ 10,743 -
$ \Delta $ - 3,360,292
$ \mathcal{N}$ 26,998 43,366,308
Partial Rebuild 513.8 s
Complete Rebuild 1113.7 s

Table 5: Running time performance of the partial rebuild method using landmark-diff and the complete rebuild method. The symbols $ \mathcal{D}$, $ \mathcal{C}$, $ \Delta $$ \mathcal{C}$, $ \Delta $ and $ \mathcal{N}$ denote the deleted documents, the common documents, the common documents that have changed, the update operations for the common documents and the new documents that have been inserted. We give the sizes of these sets in units of documents as well as postings.

The partial rebuild using landmark-diff method results in a speedup of 2 over a complete rebuild of the index using k-way mergesort even for two samples that are 71 hours apart and thus have a large number of changed common documents and inserted documents.

4.5 Discussion

Updating inverted indexes given a new sample of the web involves four sets of items:

  1. the postings of deleted documents $\ensuremath{\mathcal{D}}$,
  2. the postings for inserted/new documents $\ensuremath{\mathcal{N}}$,
  3. the postings for common documents $\ensuremath{\mathcal{C}}$, and
  4. the update operations $\ensuremath{\Delta}$ for $\ensuremath{\mathcal{C}}$.

The existing inverted index (consisting of $\ensuremath{\mathcal{C}}$ and $\ensuremath{\mathcal{D}}$) has to be `merged' with the sets $\ensuremath{\mathcal{D}}$, $\ensuremath{\mathcal{N}}$ and $\ensuremath{\Delta}$, so that $\ensuremath{\mathcal{D}}$ is deleted, $\ensuremath{\mathcal{N}}$ is inserted, and $\ensuremath{\Delta}$ is applied to the inverted index (the alternative is to rebuild from scratch). The set $\ensuremath{\mathcal{D}}$ can be processed very efficiently by storing the doc_ids using a bit map. Updating the index with $\ensuremath{\Delta}$ can be done very efficiently using our landmark-diff method (three times faster than the forward index method). The efficiency of incorporating $\ensuremath{\mathcal{N}}$ to the inverted index will depend on the size of $\ensuremath{\mathcal{N}}$.

The partial rebuild using landmark-diff exploits the following two facts to achieve the factor of two speedup: (1) the large $\ensuremath{\mathcal{N}}$ (relative to $\ensuremath{\mathcal{C}}$) can be processed in a sequential manner very efficiently; (2) our landmark-diff method produces a very small $\ensuremath{\Delta}$ relative to $\ensuremath{\mathcal{C}}$ very efficiently. The goal of this paper is to investigate fast incremental update of inverted index. As the sampling interval decreases, the sizes of $\ensuremath{\mathcal{N}}$ and $\ensuremath{\Delta}$ also decrease relative to $\ensuremath{\mathcal{C}}$ [ 7]. In the limit, $\ensuremath{\mathcal{N}}$ will be very small and random access updates to an inverted index implemented as a B-tree will be faster than an array implementation. A similar trade-off between random access data structures and stream-based processing has been observed in the processing of spatial joins [1]. Therefore, the speedup in incremental update time using a B-tree implementation approaches

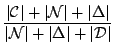
$\displaystyle {\frac{{\vert\ensuremath{\mathcal{C}}\vert + \vert\ensuremath{\ma... ...}}\vert + \vert\ensuremath{\Delta}\vert + \vert\ensuremath{\mathcal{D}}\vert}}}$ (1)

compared with a complete rebuild. We have showed in Table 5 that the array-based partial rebuild using landmark-diff is twice as fast as complete rebuild for a relatively large update interval of 71 hours. As the update interval gets smaller, the speedup will be more significant and even more dramatic if we use a B-tree implementation of the inverted index.

5 Conclusion

Keeping web indexes up-to-date is an important problem for research and in practice. Naive update methods such as index rebuild is inadequate in keeping the inverted index up-to-date especially in the context of in-place, incremental crawling. That web document changes are generally small and clustered, motivates the use of incremental update algorithms based on diff. However, storing positional information in the inverted index presents a problem in using the diff approach. The landmark representation that we proposed allows the diff approach to be used to efficiently update inverted indexes that store positional information. Our experiments show that our method results in significant savings in the number of edit operations performed on the inverted index and hence in the update time. We further showed how the landmark-diff method can be used with partial rebuild to update inverted index in half the time it takes to rebuild the index from scratch.

Bibliography

[1] L. Arge, O. Procopiuc, S. Ramaswamy, T. Suel, J. Vahrenhold, and J. S. Vitter. A unified approach for indexed and non-indexed spatial joins. Proceedings of the 7th Intl. Conf. on Extending Database Technology (EDBT '00), 1777, 413-429, 2000.

[2] R. Baeza-Yates and B. Ribeiro-Neto. Modern Information Retrieval. Addison-Wesley, 1999.

[3] R. S. Boyer and J. S. Moore. A fast string searching algorithm. Communications of the ACM, 20, 762-772, 1976.

[4] B. Brewington and G. Cybenko. Keeping up with the changing web. IEEE Computer, 33(5), 52-58, May 2000.

[5] E. W. Brown, J. P. Callan, and W. B. Croft. Fast incremental indexing for full-text information retrieval. In 20th Intl. Conf. on Very Large Data Bases, 192-202, 1994.

[6] J. Cho and H. Garcia-Molina. Estimating frequency of change. Submitted for publication, 2000.

[7] J. Cho and H. Garcia-Molina. The evolution of the web and implications for an incremental crawler. 26th Intl. Conf. on Very Large Data Bases, 2000.

[8] C. Clarke and G. Cormack. Dynamic inverted indexes for a distributed full-text retrieval system. Tech. Report CS-95-01, Univ. of Waterloo CS Dept., 1995.

[9] C. Clarke, G. Cormack, and F. Burkowski. Fast inverted indexes with on-line update. Tech. Report CS-94-40, Univ. of Waterloo CS Dept., 1994.

[10] D. Cutting and J. Perdersen. Optimizations for dynamic inverted index maintenance. Proceedings of SIGIR, 405-411, 1990.

[11] W. Frakes and R. Baeza-Yates, editors. Information Retrieval: Data Structures and Algorithms. Prentice-Hall, 1992.

[12] D. E. Knuth, J. H. Morris, and V. B. Pratt. Fast pattern matching in strings. SIAM Journal of Computing, 6, 323-350, 1977.

[13] S. Lawrence and C. L. Giles. Accessibility of information on the web. Nature, 400, 107-109, 1999.

[14] Q. Li and B. Moon. Indexing and querying xml data for regular path expressions. In 27th Intl. Conf. on Very Large Data Bases, 361-370, 2001.

[15] L. Lim, M. Wang, S. Padmanabhan, J. S. Vitter, and R. C. Agarwal. Characterizing web document change. In Advances in Web-Age Information Management, 2nd Intl. Conf., WAIM 2001, 133-144, 2001.

[16] U. Manber and S. Wu. GLIMPSE: A tool to search through entire file systems. In Proceedings of the Winter 1994 USENIX Conf., 23-32. USENIX, 1994.

[17] S. Melnik, S. Raghavan, B. Yang, and H. Garcia-Molina. Building a distributed full-text index for the web. Proceedings of the 10th Intl. WWW Conf., 2001.

[18] L. Page and S. Brin. The anatomy of a large-scale hypertextual web search engine. Proceedings of the 7th Intl. WWW Conf., 107-117, 1998.

[19] A. Tomasic, H. Garcia-Molina, and K. Shoens. Incremental updates of inverted lists for text document retrieval. Proceedings of 1994 ACM SIGMOD Intl. Conf. of Management of Data, 289-300, May 1994.

[20] E. Ukkonen. Algorithms for approximate string matching. Information and Control, 64, 100-118, 1985.

[21] J. S. Vitter. Faster methods for random sampling. Communications of the ACM, 27, July 1984.

[22] J. S. Vitter. An efficient I/O interface for optical disks. ACM Trans. on Database Systems, 129-162, June 1985.

[23] I. H. Witten, A. Moffat, and T. C. Bell. Managing Gigabytes: Compressing and Indexing Documents and Images. Morgan Kaufmann Publishers, Los Altos, CA 94022, USA, second edition, 1999.

[24] C. Zhang, J. F. Naughton, D. J. DeWitt, Q. Luo, and G. Lohman. On supporting containment queries in relational database management systems. In Proceedings of 2001 ACM SIGMOD Intl. Conf. of Management of Data, 361-370, 2001.

Footnotes

[... Lim1]  Work done while the author was visiting IBM T. J. Watson Research Center.

[... Vitter2]  The author was supported in part by the Army Research Office through grant DAAD19-01-1-0725, by the National Science Foundation through research grants CCR-9877133 and EIA-9870724, and by an IBM Faculty Award.

[... memory3]  For example, Google has thousands of machines with at least 8 GB of memory each.

[... analysis4]  The data consists of several samples of web documents crawled from five seed URLs every 12 hours.

[... keyword5]  The keyword with the smallest frequency.

[... size6]  The reasoning is similar to a 2-level B-tree where the number of blocks and the block size is `balanced'.