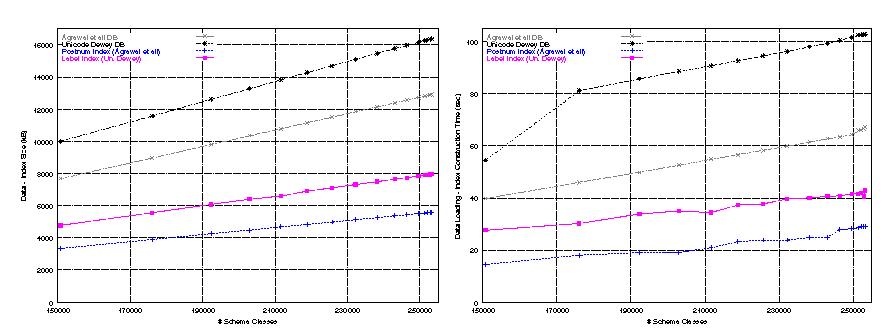
Figure 4: a) Database/Index Size and b) Construction Time for ODP Subclass Trees
4.1 The Case of Trees
We first choose a relational representation of
UPrefix and
PInterval labels in order to compare the resulting database
size. The performance of the testbed queries (see
Table
2) is then compared when implemented with the
PostgreSQL engine.
4.1.1 Database Representation and Size
The RDF/S class (or property) hierarchy of a Portal Catalog like ODP,
can be represented by one table with two attributes: the name of the
class (primary key) and the name of its father class. Because in ODP
the class names are large variable size strings (path from root
including namespace and path prefix) we choose the following
normalized relational database schema:
Class(id:int4, name:varchar(256))
SubClass(id:int4, father:int4)
where
id is a class identifier,
name is its name, and
father is the father class identifier.
Since the labels produced by
UPrefix or
PInterval are unique, they
can be used (or a part of them) as identifiers of classes in the
tree. In the following, we evaluate the database and index size of the
following tables replacing
SubClass respectively by:
UPrefix(label:varchar(15), father:varchar(15))
PInterval(index:int4, post:int4, father:int4)
where
father respectively stores the father's string label or
post-number value.
Two remarks are noteworthy. First the string type of attribute
label in
UPrefix is determined by the maximum depth of the ODP
class hierarchy (see Table
1) plus one (for the root
class
Resource) while the type of the
post (and
index) attribute in
PInterval by the total number of the ODP
classes. Second, in both cases we utilize the
father attribute
in order to reconstruct the class hierarchy in RDF/S from the database
as well as to efficiently support direct parent/children/sibling
queries. This choice is justified by the significant evaluation cost
of these queries in SQL engines with user-defined functions like
prefix in
UPrefix or additional information on node labels like
depth in
PInterval (otherwise finding the direct children of
Resource requires a complete scan of the ODP hierarchy!).
Figure
4-a displays the size of the database (tables
UPrefix and
PInterval) and the size of the index (respectively on
attributes
label and
post) while Figure
4-b displays the
construction time when the 16 ODP hierarchies (see
Table
1) are loaded in decreasing order of their number
of classes. More precisely, the size of table
UPrefix is 16376 Kb
and the size of
PInterval is 12902 Kb both containing 253215 tuples
(i.e., classes) on 2073 and 1613 disk pages respectively.
Equivalently, to store the label of a class as well as the label of
its superclass (i.e., a tuple) we need 52,17 bytes with
PInterval
and 66.22 bytes with
UPrefix. Compared to the
PInterval 12 bytes
expected from the schema, the extra storage cost per tuple is due to
an id (40 bytes) generated by PostgreSQL to identify the physical
location of a tuple within its table (block number, tuple index within
block). In addition, the PostgreSQL storage requirement for string
types is 4 bytes plus the actual string size. For these reason we need
on the average
9 13.11 bytes for storing the class
label in
UPrefix. It should also be emphasized that only 0.133% of
the encoded classes (2 classes have a fan-in degree > 256 with 336
subclasses) in
UPrefix require labels with Unicode characters
exceeding the two bytes.
Table
UPrefix is 21.2% bigger than
PInterval, while the size of
the index on attribute
label is 29.8% larger (1001 disk pages) than
that of
post (697 disk pages). On the other hand, data loading
(index construction) time of
UPrefix is 34,75% (32,21%) larger
than of
PInterval. Slightly smaller size and time have been obtained
for the indices on attribute
father in both tables (due to the
indexing of smaller ranges of values). Clearly, the extra storage cost
of
PInterval is due to a significant overhead for storing and
indexing strings in the PostgreSQL DBMS.
4.1.2 Core Query Evaluation
In this subsection, we are interested in the efficient implementation
of the Portal query functionality for both prefix and interval
labeling schemes using standard SQL engines. Most query expressions
(see Table
2) can be directly translated into SQL,
using the relational schema of the previous section. The only queries
for
UPrefix needing to be implemented by SQL stored procedures are
ancestors (function
prefixes) and
nca (functions
prefixes and
mlength). Stored procedures are also employed to
implement the
subsumption checking on two class labels for both
schemes. It should be stressed that for optimization reasons queries
such as
leaves for
UPrefix and
followings for
PInterval need to be rewritten.
More precisely, the main performance limitation of SQL queries for
UPrefix is due to the presence of user-defined functions (
next,
prev and
mprefix) in the selection conditions involving the
attribute
label. Such queries are evaluated by the SQL engine
without taking into account the existence of an index defined on
label. To solve this limitation, when possible user-defined functions
are evaluated prior to the execution of the SQL query. For instance,
the query
descendants of the root class
Resource uses the
condition
label >
'1' Ù label <
next('
1').
Since function
next is applied to the input node of the query (e.g.,
the label '
1' of
Resource) the condition can be replaced
by
'1' Ù label <
'2' (
next('
1')=
'2') where
next has been pre-evaluated. However, this rewriting is
not always possible, as in query
leaves where the function
next is used in the nested subquery over the labels returned by the
outer block:
|
select |
label |
| from |
UPrefix |
| where |
label > 'l' and label <'ln' and |
|
not exists ( |
select |
* |
|
|
from |
UPrefix u' |
|
|
where |
u'.label > label and |
|
|
|
u'.label < next(label))
|
For this reason, the previous query was rewritten so as to involve
only string operations and not functions on
label:
|
select |
label |
| from |
UPrefix |
| where |
label > 'l' and label < 'l' || 'xFF' and |
|
not exists ( |
select |
* |
|
|
from |
UPrefix u' |
|
|
where |
u'.label > label and |
|
|
|
u'.label' < label || 'xFF')
|
The string operator
|| concatenates the Unicode character 'xFF'
(``all-ones'' byte) to the value of attribute
label. The resulting
string is the maximal string inferior to
next(
label)
10. Then the index can be used during the evaluation of
the nested query. Other rewritings were experimented with (e.g., using
structural information represented by attribute
father) but the
previous solution exhibited the best performance.
| Query |
PInterval |
UPrefix |
| |
| Case 1 |
Case 2 |
Case 3 |
| %Select |
%Select |
%Select |
|
| Case 1 |
Case 2 |
Case 3 |
| %Select |
%Select |
%Select |
|
| subsumption check |
| Q1 |
| descendants |
| Q2 |
| ancestors |
| Q3 |
| leaves |
| Q4 |
| precedings |
| Q5 |
| followings |
| Q6 |
| siblings |
| Q7 |
| nca |
|
| 0,00018 |
0,00018 |
0,00017 |
| 2,869392 |
0,429730 |
0,00027 |
| 100% |
10% |
0,0004% |
| 1,18904 |
1,54799 |
0,00027 |
| 0,002% |
0,00158% |
0,00355% |
| 2,957039 |
0,493230 |
0,00027 |
| 75,13% |
8,46% |
0,0004% |
| 2,629188 |
2,34529 |
0,00024 |
| 100% |
50% |
0% |
| 2,9721 |
2,48579 |
0,00024 |
| 100% |
50% |
0% |
| 0,00863 |
0,00054 |
0,00047 |
| 0,1236% |
0,002% |
0,0004% |
| 3,22742 |
0,00041 |
0,000438 |
| 0,0004% |
0,0004% |
0,0004% |
|
| 0,00017 |
0,00017 |
0,00017 |
| 3,296126 |
0,57702 |
0,00027 |
| 100% |
10% |
0,0004% |
| 0,00163 |
0,00178 |
0,00167 |
| 0,002% |
0,00158% |
0,00355% |
| 25,54267 |
16,51963 |
0,00055 |
| 75,13% |
8,46% |
0,0004% |
| 2,874457 |
126623 |
0,0005 |
| 100% |
50% |
0% |
| 3,37825 |
2,566292 |
0,0005 |
| 100% |
50% |
0% |
| 0,00961 |
0,00056 |
0,00049 |
| 0,1236% |
0,002% |
0,0004% |
| 0,0003945 |
0,0003945 |
0,0003945 |
| 0,0004% |
0,0004% |
0,0004% |
|
Table 3: Execution Time of Core Queries for the ODP Subclass Tree
The only problem for the interval based scheme is related to the
followings query. It relies on the values of the attribute
index
for which no index was constructed. In order to use only the available
index on
post, we rewrite the query as follows:
|
select |
post |
| from |
PInterval |
| where |
post > p and index > i
|
The selection condition is equivalent to the original one
index >
p
(in
PInterval following nodes have always greater postorder and
index numbers
11) and query evaluation can be optimized with the use of the
B-tree defined on
post.
Except for the two previous rewritings, the evaluation of the core
queries with the two labeling schemes strictly uses the conditions
stated in Table
2. Each query was run several times:
one initially to warm up the database buffers and then nine times to
get the average execution time of a query. Recall that 1000 buffers of
size 8KB and thus the indices of attributes
label (1001 disk pages)
and
post (697 disk pages) can fit entirely in main memory.
Table
3 gives the resulting execution time in
seconds (using PostgreSQL
Explain Analyze facility) for both
schemes and for up to three different cases per query: each case
corresponds to a different choice of input node and therefore of query
selectivity.
The main observation is that the query performance of the two labeling
schemes is comparable. The
leaves query is penalized in
UPrefix by the use of nested queries. Compared to
PInterval,
ancestors and
nca run with the former scheme in practically
constant time. In all other queries,
PInterval exhibits slightly
smaller execution times than
UPrefix since for the same number of
returned tuples a smaller number of disk pages need to be accessed.
Finally, PostgreSQL (cost-based) query optimizer seems to favor index
scans on tables
UPrefix and
PInterval although sequential scans
should be more efficient (e.g., in queries with 50% selectivity!).
This is due to inaccurate selectivity estimations (higher) of query
predicates especially for string comparisons in
UPrefix. The same
plans and comparable execution times for all queries have been
observed when augmenting the number of buffers from 1000 to 10000.
In
Q1 each case corresponds to the choice of a different node
for which the descendants are computed: (a) in Case 1 the root (i.e.,
Resource) (b) in Case 2 a node with a medium number of
descendants (i.e.,
Arts) and (c) in Case 3 a node with a minimum
number of descendants. In Cases 2 and 3, the node label appears in the
middle of the
post or
label intervals of values. PostgreSQL
optimizer chooses for both labeling schemes a sequential scan for the
first case and index scans for the other two. Since the interval query
is based exclusively on
post (e.g.,
i <=
post <
p) or
label
(e.g.,
l <
label <
l') index scan is beneficial: the optimizer uses
the index to access the tuple satisfying the lower bound condition and
since the examined index keys are sorted, it stops sequential scan of
tuples when the upper bound is reached.
The three cases of input nodes for
Q2 correspond to (a) the
leftmost (b) a middle and (c) the rightmost leaf of the ODP subclass
tree. The response time is significantly better for the Prefix scheme
in the first two cases. PostgreSQL optimizer chooses for
PInterval
(for
UPrefix stored procedures are used) a sequential scan for Case
1 and index scans for Cases 2 and 3. The interval query is based now
on different attributes namely
post and
index (
index <=
p Ù
p <
post since for leaves
index=
post) and all values returned by
the index scan (on
post) have to be scanned to check the first
condition (on
index). The wrong selectivity estimation for the
conjunction leads the optimizer to favor in Case 2 an index scan (on
the half interval) which turns out to be much more costly than a
sequential one (on the entire interval)!
Q3 is evaluated with the same input nodes as
Q1. Thus, for
PInterval, the PostgreSQL optimizer chooses the same plans in the
three cases. The slightly higher execution times compared to
Q1
are due to the evaluation of the extra condition for leaves
(
index=
post) given that the number of accessed disk pages are the
same. On the other hand,
UPrefix is significantly penalized by the
use of the nested query: index scans are used for the nested query in
all cases while a sequential scan should be used at least for Case 1.
Queries
Q4 and
Q5 employ the same input nodes as
Q2
and the three cases for
precedings and
followings have
inverse selectivities. The execution times for queries with zero
selectivities (Case 3) give us an indication about the lookup cost of
indices defined on attributes
post and
label.
Q6 is evaluated with input nodes having the maximum, a medium
and the minimum fan-in degrees of ODP subclass trees. It involves a
nested loop join over two index scans: one to find the father of a
node and the other to find its direct siblings using equality
on
post (
label) and
father.
Finally,
Q7 takes as an input a pair of nodes (using the same
leaves as in
Q2): in Case 1 the leftmost-rightmost leaves, in
case 2 the leftmost-middle leaf and in Case 3 the middle-rightmost
leaves. For
UPrefix a stored procedure is executed, while for
PInterval a nested query is evaluated using index scans for both the
inner and outer blocks in the three cases. In Case 1 the resulting
time for the interval based scheme is significant. However as
aforementioned, a sequential scan should be chosen. For Cases 2 and 3
the response times are comparable.
4.2 The Case of DAGs
In this section we first present the relational representation of
UPrefix and
PInterval labels in the case of a subclass DAG and
evaluate the extra storage cost for both labeling schemes. We then
show, as for the case of trees, how
subsumption check,
descendant,
ancestor,
leaves,
siblings and
nca queries (
preceding and
following queries are not
defined on DAGs) can be expressed on the label representation of the
hierarchy and translated into SQL queries. We end up our study by a
performance comparison of the two schemes in terms of query response
time.

Figure 5: Label Propagation and Compression for ODP Subclass DAGs
4.2.1 Database Representation and Size
In each labeling scheme, two tables are now necessary for representing
the class hierarchy, apart from table
Class with attributes
id
and
name. The first table in both schemes is the same as in the
case of trees (
UPrefix,
PInterval). The only modification is that
for DAGs, tuples in these tables represent both kinds of edges
(spanning-tree or non-spanning-tree edges). The rationale behind this
choice is that
siblings (and father/children) queries can be
easily evaluated on tables
UPrefix and
PInterval using the
father attribute (as in the case of trees). This choice implies the
extension of both tables key in order to include the
father
attribute, as follows:
UPrefix(label:varchar(15), father:varchar(15))
PInterval(index:int4, post:int4, father:int4)
It should be stressed that when label compression in
PIn-
terval
also considers the merging of adjacent intervals, DAG nodes are not
anymore identified using their postorder number. For instance, in
Figure
3 both nodes
C and
G have as a
post
value
5. As shown in the following, the total label compression
gains from merging is less than 0.6% and therefore we do not consider
this compression in the following.
The second table is respectively called
DUPrefix and
DPInterval in
the two schemes where
D stands for DAG. In the former table, tuple
(
label,
ancestor) indicates that the node with label
ancestor
propagates
downwards its label to the node identified by
label. In the latter, tuple (
index,
post,
ancestor) indicates
that the node with label [
index,
post] propagates its label
upwards to the node identified by the post value
ancestor. Keys are
not mandatory for these tables because they are not accessed
independently from the primary table (indices have been defined on
attributes
ancestor and
label or
post).
DUPrefix(label:varchar(15), ancsestor:varchar(15))
DPInterval(index:int4, post:int4, ancsestor:int4)
Looking at Figure
3, left, the label
[6,3] of
G is propagated up only to
B since it is absorbed by
A. Then
DPInterval includes one tuple (3,5,2) where 3,5 account
for the
index and
post values of
G and 2 for the
post
value of
B (i.e., its id). Similarily the
DUPrefix table
includes the two tuples ('1121','111'), and ('11212','111') that
account for the propagation of
B's label down to its descendants
G, and
I (for
H,
B's label is absorbed by the
propagated label '1111' of
D). Note the redundancy of the
attribute
index, since any node is identified by its post value.
This redundancy allows for a faster SQL execution of the
descendants query. It should be stressed that when label compression
is not considered in both schemes, table
DUPrefix (
DPInterval)
essentially materializes the result of
descendents
(
ancestors) query involving DAG edges.
Let us now evaluate the extra storage cost for labeling DAGs with the
two schemes. Since in both cases the tables
UPrefix and
PInterval
hold all the edges of the DAG (to enable reconstruction in RDF/S), the
extra storage space is exactly the size of tables
DUPrefix and
DPInterval: for each scheme we only need to measure the number of
propagated labels. This (downwards or upwards) propagation depends on
the position of the source and target nodes of the non spanning tree
edges in the DAG or more precisely the number of descendants
(ancestors) of source (target) nodes. The DAG testbed uses the ODP
hierarchies (see Table
1) augmented with synthetically
generated multiple
isA links. The original ODP classes are
decomposed into three sets according to their depth in the tree: a)
near to the root (denoted
R); b) near to the leaves (denoted
L);
and c) in between (denoted
B). Then, picking at random the source
and target edge classes, additional edges are equally distributed in
nine groups:
RR,
RL,
RB, etc. In addition, the maximum fan-out
degree of classes is fixed to 2 (a typical upper bound of multiple
isA links as observed in [
18]).
The total number of label propagations is displayed in
Figure
5 versus the percentage of additional edges. The
experiment was conducted incrementally until the number of original
ODP tree edges is doubled (100% percentage of additional edges): for
every 5% generated edges, we execute the two labeling algorithms.
Note that the spanning tree computed (for both algorithms) is
different at each increment step. The main observation from
Figure
5 is that the number of label compressions in
PInterval is proportional to the number of additional edges,
regardless of their positioning in the DAG, which is not the case for
UPrefix. For this reason, the number of label propagations for
PInterval is stabilized between 50000-80000, while for
UPrefix it
seems to depend on the actual number of descendants of the source
class of each additional edge. Clearly, when a significant number of
edges has been added (e.g., 65%) label propagation in the two schemes
diverges significantly. In addition, the number of adjacent label
mergings in
PInterval is always smaller than the number of subsumed
label absorptions, while ignoring labels' merging (in order to
maintain postorder numbers as class identifiers) implies only 2492
additional tuples in
DPInterval (i.e., 4%). Practically speaking,
for 253214 additional edges (i.e., 100%)
DUPrefix will contain
179270 tuples and
DPInterval 63937 (i.e., 61445 plus 2492) when
compression is based only on the absorption of subsumed labels. This
DAG testbed will be used in the sequel for evaluating the query
performance of both labeling schemes. When labels' compression is
completely ignored, the size of table
DPInterval is three times
bigger, while
DUPrefix has almost the same size (due to the very
small numbers of compressions).

Table 4: Core Query Expressions for DAGs: a) DUPrefix, b) DPInterval
4.2.2 Core Query Evaluation
In Table
4, we provide, for both labeling schemes,
a declarative formulation of the five testbed queries expressed in
terms of the query expressions defined for the tree case. We denote by
Propdown(
u) in
DUPrefix the set of descendant nodes of
u to
which
u's label is propagated and by
Propansc(
v) the set of
ancestors
u of
v such that
v Î Propdown(
u). Similarily,
Propup(
u) in
DPInterval is the set of ancestor nodes of
u to
which the label of
u is propagated as an additional label and
Propdesc(
v) is the set of descendants
u of
v such that
v Î
Propup(
u). Subsumption checking for two DAG nodes
u and
v
evaluates to true in
DUPrefix (
DPInterval) iff the
subsumption(
u,
v) condition given in the case of trees (see
Table
2 columns 2,3) is true or
u Î Propansc(
v)
(
v Î Propup(
u)). In the sequel, we provide the SQL translation of
the declarative expressions for
Ddescendants,
Dancestors and
Dleaves. Clearly, label compression result to more complicated query
expressions because the paths connecting two DAG nodes through non
spanning tree edges are not completely materialized in tables
DUPrefix and
DPInterval. On the other hand, it ensures that no
descendant/ancestor is computed more than once when querying both the
tables
UPrefix (or
PInterval) and
DUPrefix (or
DPInterval). In
other words, we don't need to eliminate duplicates in the union of the
two subqueries (i.e., for computing tree and DAG
descendants/ancestors).
Query
Ddescendants(
v) uses the
descendants(
v) expression given for
the case of a tree (see Table
2, columns 2,3). In
both schemes, it also finds the descendants related to propagated
labels of
v, respectively given by
Propdown(
v) and
Propdesc(
v). In the absence of compression, the expression
Propdown(
v) would be expressed by the following simple SQL query,
where '
l' denotes the label of
v (
UPrefix):
|
select label from DUPrefix where ancestor= 'l'
|
Because of the label compression the corresponding SQL query employs
also a nested query on
UPrefix for finding the descendants in paths
involving DAG edges:
|
select |
w.label |
| from |
DUPrefix w, |
(select |
u.label as label |
|
|
from |
UPrefix u |
|
|
where |
u.label >= 'l' and |
|
|
u.label |
< 'l' || 'xFF') u' |
| where |
w.ancestor = u'.label
|
Denoting the label of
v by
[i,p] (
PInterval) the union
subquery on
Propdesc(
v) is translated into SQL as follows:
|
select |
u.post |
| from |
PInterval u, DPInterval w |
| where |
w.ancestor = p and u.post >= w.index |
|
and u.post <= w.post
|
The query
Dancestors(
v) relies in turn on the
ancestors(
v)
expression given for the case of a tree. In both schemes, it also
considers the ancestors related to propagated labels of
v which are
given respectively by the expressions
Propansc(
v) and
Propup(
v).
The SQL translation of
Propup(
v) for
DPInterval with label
compression is given below:
|
select |
w.post |
| from |
PInterval w, DPInterval v, |
|
(select |
u.post as post |
|
from |
PInterval u |
|
where |
u.index <= i and u.post >= p) u' |
| where |
w.index |
<= v.ancestor and w.post >=v.ancestor |
|
and v.post = u'.post
|
The query
Dancestors(
v) for
DUPrefix is translated into a stored
procedure which employs an intermediate SQL query to compute the
expression
Propansc(
v):
|
select ancestor from DUPrefix where label= 'l'
|
For query
Dleaves(
v) we obtain the following SQL translation in
DPInterval (for
DUPrefix, the SQL query is similar and uses the
SQL translation of
Ddescendants):
|
select |
u.post |
| from |
PInterval u |
| where |
u.post < p and u.post >= i and u.post = u.index |
|
and not exists ( |
select |
* |
|
|
from |
DPinterval u' |
| Union All |
|
where |
u'.ancestor = u.post) |
| select |
u.post |
| from |
PInterval u, DPInterval w |
| where |
w.ancestor = p and u.post >= w.index |
|
and u.post <= w.post |
|
and not exists ( |
select |
* |
|
|
from |
DPinterval u' |
|
|
where |
u'.ancestor = u.post)
|
Dsiblings(
v) has exactly the same expression as for the tree
case. Due to space limitations, we do not give the full expressions on
labels for
Dnca(
v,
w) but we use
Dancestors as a short-hand
notation. Similarly, its SQL translation uses nested subqueries in
DPInterval as the above expression for
Dancestors. In
DUPrefix
however the expression is much simpler since it relies on string
functions (see Table
2).
Table
5 shows the execution times of the testbed
queries for the synthetically generated ODP DAGs (100% of
Figure
5) using the same input nodes as in the case of
trees (see Table
3). Due to the additional DAG
edges (on the same ODP nodes) the size of tables
UPrefix and
PInterval is practically doubled and the query selectivities are
accordingly increased, despite the fact that additional nodes are
returned by some of our queries. The main observation is that
DPInterval outperforms
DUPrefix by up to 5 orders of magnitude for
descendants and
leaves queries especially for cases (i.e,
3) with high selectivity. This is due to the evaluation of the
nested subqueries in the from clause of these queries using
merge-joins over string attributes. String sorting exhibited
unacceptable execution time in PostgreSQL, compared to integer sorting
involved in the evaluation of the
ancestors query in
DPInterval using the same execution plan. On the other hand,
ancestors and
nca in
DUPrefix run in practically constant
time. Although not detailed in this paper, when we ignore label
compression, no significant performance gains are obtained for both
schemes due to the extra cost of label's sorting and duplicate
elimination (i.e.,
Union vs.
Union All) in queries,
especially for string labels.
| Query |
DPInterval |
DUPrefix |
| |
| Case 1 |
Case 2 |
Case 3 |
| %Select |
%Select |
%Select |
|
| Case 1 |
Case 2 |
Case 3 |
| %Select |
%Select |
%Select |
|
| Q1 |
| descendants |
| Q2 |
| ancestors |
| Q3 |
| leaves |
| Q4 |
| siblings |
| Q5 |
| nca |
|
| 11,92988 |
0,617279 |
0,000263 |
| 50% |
5,051% |
0,0004% |
| 3,790538 |
2,6323 |
3,095479 |
| 0,033% |
0,00454% |
0,00276% |
| 14,50642 |
1,57837 |
0,000087 |
| 21,55% |
2,211% |
0,0002% |
| 0,002591 |
0,002442 |
0,00033 |
| 0,0626% |
0,0008% |
0,0004% |
| 4,870160 |
4,691551 |
3,70287 |
| 0,0002% |
0,0002% |
0,0002% |
|
| 67,12124 |
21,78665 |
20,4409 |
| 50% |
5,051% |
0,0004% |
| 0,00619 |
0,00514 |
0,00472 |
| 0,033% |
0,00454% |
0,00276% |
| 95,58222 |
48,192656 |
47,297535 |
| 21,55% |
2,211% |
0,0002% |
| 0,003011 |
0,002946 |
0,00032 |
| 0,0626% |
0,0008% |
0,0004% |
| 0,00058 |
0,00057 |
0,00055 |
| 0,0002% |
0,0002% |
0,0002% |
|
Table 5: Execution Time of Core Queries for the ODP Subclass DAG
5 Summary
A number of interesting conclusions can be drawn from the conducted
experiments. Firstly, for voluminous class
subsumption
hierarchies, labeling schemes bring significant performance gains (3-4
orders of magnitude) in query evaluation as compared to transitive
closure computations [
14]. Secondly, this gain
comes with no significant increase in storage requirements for the
case of tree-shaped hierarchies especially for the interval scheme
while the query performance for both schemes is comparable. For
DAG-shaped hierarchies, we need for the interval (prefix) scheme up to
2.4 (2.7) times more storage space when the propagated labels are
compressed. In particular, for practical cases (i.e., small percentage
of added non tree edges) the interval scheme is less sensitive than
the prefix one, to the propagation of labels w.r.t. the actual
position of the source and target nodes of the added DAG edges.
Significant divergent behavior in labels' propagation is observed when
the percentage of the added DAG edges increases substantially (>
65%). Thirdly, for
descendants and
leaves queries on
DAGs, interval schemes are up to five times more costly than in the
case of trees, compared to prefix ones which are up to 5 orders of
magnitude more costly. However,
ancestors and
nca in
DUPrefix run in practically constant time for both tree and
DAG-shaped hierarchies. When labels' compression is ignored, the two
schemes exhibit almost the same storage requirements while their query
performance is slightly improved. The bad performance of the prefix
scheme is due to the PostgreSQL questionable choice of optimization
strategies for complex queries involving string attributes and their
surprisingly slow execution time. We are planning to study this issue
w.r.t. other DBMS.
References
- [1]
-
R. Agrawal, A. Borgida, and H. V. Jagadish.
Efficient management of transitive relationships in large data and
knowledge bases.
In Proc. of the SIGMOD Inter. Conf. On Manag. Of Data,
pages 253--262, 1989.
- [2]
-
H. Aït-Kaci, R. Boyer, P. Lincoln, and R. Nasr.
Efficient implementation of lattice operations.
ACM Trans. on Progr. Languages and Systems, 11(1):115--146,
1989.
- [3]
-
S. Alexaki, G. Karvounarakis, V. Christophides, D. Plexousakis, and K. Tolle.
The ICS-FORTH RDFSuite: Managing Voluminous RDF
Description Bases.
In 2nd Inter. Workshop on the Semantic Web, pages 1--13, 2001.
- [4]
-
D. Brickley and R.V. Guha.
Resource Description Framework (RDF) Schema Specification 1.0, W3C
Candidate Recommendation, 2000.
- [5]
-
Y. Caseau.
Efficient handling of multiple inheritance hierarchies.
In OOPSLA'93, 1993.
- [6]
-
Online Computer Library Center.
Dewey decimal classification.
Availiable at www.oclc.org/dewey/.
- [7]
-
S.-Y. Chien, Z. Vagena, D. Zhang, V. J. Tsotras, and C. Zaniolo.
Efficient structural joins on indexed xml documents.
In Proc. of the Inter. Conf. On Very Large Data Bases
(VLDB'02), 2002.
- [8]
-
E. Cohen, H. Kaplan, and T. Milo.
Labeling dynamic xml trees.
In Proc. of the Twenty-first Symposium on Principles of Database
Systems (PODS'02), 2002.
- [9]
-
B. Cooper, N. Sample, M. J. Franklin, G. R. Hjaltason, and M. Shadmon.
A fast index for semistructured data.
In Proc. of the Inter. Conf. On Very Large Data Bases
(VLDB'01), 2001.
- [10]
-
P. F. Dietz.
Maintaining order in a linked list.
In Proc. of the Fourteenth Annual ACM Symposium on Theory of
Computing (STOC'82), pages 122--127, 1982.
- [11]
-
P. F. Dietz and D. D. Sleator.
Two algorithms for maintaining order in a list.
In Proc. of the Sixteen Annual ACM Symposium on Theory of
Computing (STOC'87), pages 365--372, 1987.
- [12]
-
C. Gavoille and D. Peleg.
Compact and localized distributed data structures.
Journal of Distributed Computing, Special Issue for the Twenty
Years of Distributed Computing Research, 2003.
- [13]
-
H. Kaplan, T. Milo, R. Shabo.
A comparison of labeling schemes for ancestor queries.
In Proc of the Thirteen Annual Symposium on Discrete Algorithms
(SODA'02), 2002.
- [14]
-
G. Karvounarakis, S. Alexaki, V. Christophides, D. Plexousakis, and M. Scholl.
RQL: A Declarative Query Language for RDF.
In Proc. of the Eleventh Inter. World Wide Web Conf. (WWW'02),
2002.
- [15]
-
A. Krall, J. Vitek, and N. Horspool.
Near optimal hierarchical encoding of types.
In 11th European Conf. on Object Oriented Programming
(ECOOP'97), 1997.
- [16]
-
O. Lassila and R. Swick.
Resource Description Framework (RDF) Model and Syntax Specification,
W3C Recommendation, 1999.
- [17]
-
Q. Li and B. Moon.
Indexing and querying XML data for regular path expressions.
In Proc. of 27th Inter. Conf. on Very Large Data
Bases(VLDB'02), 2001.
- [18]
-
A. Maganaraki, S. Alexaki, V. Christophides, and D. Plexousakis.
Benchmarking rdf schemas for the semantic web.
In Proc. of the First Inter. Semantic Web Conf. (ISWC'02),
pages 132--147, 2002.
- [19]
-
L. K. Schubert, M. A. Papalaskaris, and J. Taugher.
Accelerating deductive inference: Special methods for taxonomies,
colours and times.
In N. Cercone and G. McCalla, editors, The Knowledge Frontier,
pages 187--220. Springer-Verlag, 1987.
- [20]
-
N. Spyratos, Y. Tzitzikas, and V. Christophides.
On personalizing the catalogs of web portals.
In Proc. of the Special Track on the Semantic Web at the 15th
Inter. FLAIRS'02 Conf., 2002.
- [21]
-
I. Tatarinov, S. Viglas, K. S. Beyer, J. Shanmugasundaram, E. J. Shekita, and
C. Zhang.
Storing and querying ordered xml using a relational database system.
In In Proc. of the SIGMOD Inter. Conf. On Manag. Of Data,
2002.
- [22]
-
A.K. Tsakalidis.
Maintaining order in a generalized linked list.
Acta Informatica, 21:101--112, 1984.
- [23]
-
S. Weibel, J. Miller, and R. Daniel.
Dublin Core.
In OCLC/NCSA metadata workshop report, 1995.
- [24]
-
N. Wirth.
Type extensions.
ACM Trans. on Progr. Languages and Systems, 10(2):204--214,
1988.
- [25]
-
F. Yergeau.
Utf-8, a transformation format of iso 10646, 1998.
Availiable at utf8.com.
- [26]
-
C. Zhang, J. F. Naughton, D. J. DeWitt, Q. Luo, and G. M. Lohman.
On supporting containment queries in relational database management
systems.
In Proc. of the SIGMOD Inter. Conf. On Manag. Of Data,
2001.
- 1
- This work
was supported in part by the European Commission project Mesmuses
(IST-2000-26074).
- 2
- See dmoz.org,
chefmoz.org,
musicbrain.org,
home.cnet.com,
www.xmltree.com, respectively.
- 3
- Note that RDF is used as an
export format for bulk catalog loading.
- 4
- For example, the catalog of the
Open Directory Portal/Dmoz comprises around 200M of Topics exported in
RDF files.
- 5
- http://www.dmoz.org/schema.rdfs. For
simplicity, we omit administrative metadata such as titles,
mime-types, modification-dates, of Web resources represented in ODP by
an OCLC Dublin-Core like schema [23].
- 6
- It is worth
noticing that the effect of multiple isA is partially captured
by terms replication in several hierarchies as well as other link
types defined between topics such as symbolic and related.
- 7
- Note that adjacent queries do not explore semantic
relationships of classes but they have been included in our study for
completeness reasons w.r.t. XML XPath expressions.
- 8
- Note that the same idea is employed by ODP in
order to identify topics/classes from the root of each hierarchy with
user readable labels, using a vocabulary of distinct terms/words (see
Table 1).
- 9
- Note that the average depth of ODP class
hierarchies including the root Resource is 8.83 (see
Table 1).
- 10
- Note
that label xFF is an imaginary rightmost child ('xFF' cannot
actually be used in a valid UTF-8 encoding) for the node with label
label whose immediate right following node has the label
next(label).
- 11
- The second condition is used to eliminate
ancestors.
This document was translated from LATEX by HEVEA.
