Online businesses are struggling to cope with the ever-increasing maintenance and ownership costs of their computing resources. Outsourcing models (e.g., Application Service Providers (ASP), Web Services) use economies of scale and shared computing to reduce these costs. Ownership costs are also reduced because of the fact that if the peak load of all its customers do not coincide in time, then the aggregated peak-to-average ratio of shared resource utilization is significantly reduced. Hence, providers could only provision resources for a fraction of the combined peaks and service the customers for most of the time. In such a finite server capacity scenario, service-level agreements (SLAs) specifying certain quality of service (QoS) guarantees (e.g., average latency < tmsec) need to be in place between a service provider and her clients. We envision that in emerging SLA-driven ASP model, requests would come with associated rewards and penalties. Penalties are incurred when the request is either not serviced at all or serviced outside the QoS bounds. Rewards, on the other hand, are obtained for servicing a request within QoS bounds. Realistically, as the resources of the service provider are less than the peak requirement, it becomes necessary to employ appropriate admission control measures to reject right subset of incoming requests so that the remaining requests can be serviced within their QoS bound.
Current web services1 suffer from unpredictability of response time that is caused by the first-come-first-serve (FCFS) scheduling model and the ``bursty'' workload behavior. Thus, under heavy load scenario if a request with small resource requirement arrives at a web service later than requests with large resource requirements, it suffers from a long delay before being serviced, causing the de facto ``denial-of-service'' effect. Anecdotal evidence suggests that service time requirements of CGI-based requests or dynamic objects are one or more than one order of magnitude greater than that for static objects [1] in a conventional web hosting scenario. The same is true for bandwidth required to deliver multimedia (text, image, audio, video) objects to a remote client from a multimedia content delivery service. Recent studies show that though the CoV (coefficient of variation) of requests is as low as 1 to 2 for each type of object, the CoV of the aggregated web object type can be of the order of 10 [2], i.e., even though the web objects of one type may be similar, the aggregation of many types of web content makes the aggregated web object highly diverse. Hence, service time requirements for various incoming requests is expected to be highly diverse. Thus, service time requirements of an incoming request must be taken into account while taking the Admission Control (AC) decision for the request.
We propose in this paper a short-term prediction based online admission control methodology to maximize the profit of the provider. To effectively handle the variability and diverseness of incoming service requests via the web, the service time of a request is utilized as the most important criterion for making AC decisions. We prove that shortest remaining job first (SRJF) based request admission policy minimizes the penalty in an offline setting. The corresponding online version of the policy is derived using short-term prediction of arrivals of future requests, their service time distribution, and capacity availability, after accounting for the capacity usage of already admitted requests. Our proposed method, in this manner, derives its effectiveness by combining the complimentary strengths of off-line and online approaches. No assumption is, however, made regarding the nature of distributions of arrival rates and service times of incoming requests. Finally we present a modification of SRJF that attempts to maximize the profit of the provider taking into account rewards and penalties associated with the requests. Experimental results are presented to demonstrate the effectiveness of the proposed AC techniques for ``bursty'' workload conditions.
Congestion control and QoS support in network transmission has been reported extensively. However, network-level QoS support is not sufficient in providing user perceivable performance without QoS support in web hosting servers, which can become heavily loaded and hence a bottleneck.
Conventional admission control schemes use a tail-dropping strategy to admit incoming requests. Under steady workload condition with similar service time requirements, queues of appropriate length along with careful capacity planning can be designed based on queueing theory models so that requests are admitted unless the queue is full. Chen and Li [4] use an essentially similar idea for AC in multimedia servers with mixed workloads. This method employs queues of different lengths for different object types, and a look-up table for online resource allocation (reservation) to adapt to workload changes. Fundamentally, variability and diversity among incoming requests tend to make queue size ineffective for making admission control decisions [2]. In PACERS (Periodical Admission Control based on Estimation of Request Rate and Service Time) algorithm [2], service time estimation is used to estimate the future capacity commitment for the already admitted (queued) requests. A new request is rejected if spare resource capacity (taking into consideration the resource requirement of queued requests) is not sufficient to service it. Thus, requests are rejected in a FIFO manner not taking into account the revenues (or service time) associated with those. Since even the requests belonging to the same class may be diverse in terms of their service time, it is necessary to choose between requests of the same class as well for maximizing the profit of the provider.
The profit maximization of service providers has been addressed by several researchers in context of self-similar, moderate workload condition (analogously, servers with sufficient capacity). Most of these address allocation of resources for various request classes with QoS guarantees so that resources are optimally utilized, thereby maximizing the profit of the providers. Among these, Liu et al. [5] proposed a multi-class queueing network model for the resource allocation problem in the offline setting, and solved it using a fixed-point iteration technique with the assumption that the average resource requirement for all the classes combined is less than the total available resource. The allocation of servers as discrete resources in a server farm has also been studied by Jayram et al. [6], keeping in mind the practical constraint that these need a finite time to be reallocated. A short-term prediction is used to make online allocation decisions, thus combining the principles of offline algorithms in an online setting. Work of similar nature has been carried in online call admission and bandwidth allocation which have been framed as cost minimization problem instead of revenue or benefit maximization [7,8,9,10]. Chang et al. [11] adopted Irani's algorithm [12]. and addressed bandwidth allocation problem for web hosting based on resource availability and assigned revenue. However, Irani's algorithm has a competitive ratio of O(logR) (where R is the reward obtained by an optimal policy). Moreover, this method too does not present any intelligent method to choose between requests of the same class.
The key idea, used in our admission control approach, is our algorithm is not blind, as most online algorithms are, but uses an expected distributions of arrivals, and service times for future requests. This allows us to effectively handle admission control problem for request arrivals of ``bursty'' nature with widely varying service time requirements (exponential or even heavy tailed). Another important distinction in our approach is the use of service time to choose between different requests for admission (interestingly, a study conducted by Joshi [13] about resource management on the downlink of CDMA Packet data networks shows that algorithms which exploit request sizes seem to outperform those that do not).
We formulate the setting and explain our system design next. In Section 3.1, we explain our approach to the problem by relaxing some constraints and presenting an offline algorithm that maximizes the number of requests serviced. We then present an online version of the algorithm that maximizes the expected number of requests serviced within their QoS bounds by using the estimated distributions. In Section 3.2 we enhance the method to maximize the difference between the sum of expected rewards and the penalties. We present performance results of our algorithms for a publish-subscribe messaging service [18] in Section 4 and conclude with our observations in Section 5.
The AC System controls the usage of some finite capacity resource (CPU, bandwidth etc.) that is used by the hosted service. It admits a subset of requests such that a pre-defined objective function is maximized. The concept of capacity of a resource is obvious in case of bandwidth [11], e.g., 128kbps. However, even for a computing service with resource like CPU, capacity can be naturally defined. For example, in a multi-threaded web-service, the maximum number of threads spawned for servicing the requests is bounded for issues of scale and performance. Hence, the number of concurrent threads or analogously the number of concurrent requests denotes the capacity.
We now give a concrete formulation of the profit maximization problem that our AC System solves. Assume an input set of n requests, where each request i can be represented as R{arrivalTime(ai), serviceTime(si), reward(Ri), penalty(Pi), responseTimeBound(bi), capacity(ci), serviceClass (Cli)}. Define C as the total capacity of the resource available and Ttot as the total time under consideration. The problem then is to find a schedule (xi,t) of requests such that the overall revenues are maximized. Formally, we have
| (1) |
|
|
åt=1Ttotxi,t = 0 implies that the request is rejected. We note that this problem can be modeled as bandwidth allocation problem which is known to be NP-Hard even in a generalized off-line setting [15]. Moreover, the problem needs to be solved in an online setting where the decision of rejecting a request is made without knowledge of the requests which are scheduled to arrive later.
A general reward and penalty model gives us the flexibility to optimize a variety of objective functions. A provider-centric model would have rewards proportional to service time. Also, in the case of differentiated services provided by the service provider, the rewards associated with a request would have the SLA class as one of the input parameter. If the SLAs have dynamic rewards, then the number of requests serviced would also be a parameter. An example for dynamic SLAs could be the following. If the provider services 90 % of the requests then the reward and penalty per request is R90, P90. However, if the total number of requests serviced is greater than 90 %, the penalty P > 90 may be less than P90. Hence, reward (and penalty) can be expressed as a function f(si, Ci, Statei) where
|
A user-centric service provider may have a reward model that tries to enhance user experience. For example, the reward model could try to minimize the average waiting time of a user's request. The algorithm should not be dependent on the pecularities of the model and the admission controller should easily adapt to a new reward model. The reward function can be formulated in terms of any set of parameters and hence we may solve the cost minimization or QoS improvement problems by solving the appropriate profit maximization problem.
In practice, one may find that reward is only related to the SLA class. Moreover, if reward is found to be dependent on service time, the dependency is linear i.e., Ri µ si or sub-linear, since a request with longer service time consumes more resource and thus should be charged more. The scenario where reward is super-linear in service time, i.e., Ri µ (si)c; c > 1, would be rare, as it would contradict the Law of Diminishing Marginal Utility [19]. Hence, an AC algorithm should be able to work well with sub-linear and linear reward models. As one may observe later, our algorithms are designed to work well with sub-linear reward models. Also, we report experiments which show that they also work well with linear reward models.
Since, by servicing a request, we are on an average expected to fetch reward proportional to the average service time of all requests, the penalty should also be related to this metric, at least in an expected sense. Also, for a request which has not been accepted, the actual service time can not be measured and the only metric available is the average. Thus, a realistic penalty model is one where the penalty for rejecting a request is proportional to average service time.
The problem of admission control of a web-based service with the objective of profit maximization poses challenges on both the system design front as well as algorithmic front. We follow a system design methodology that allows any algorithm to be plugged into the system. Similarly, the algorithm we design would be applicable to all admission control settings that can be formulated as the general maximization problem described earlier.
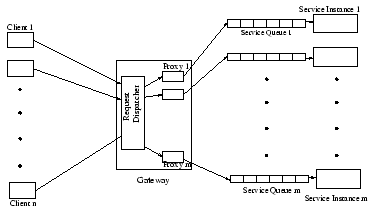
We will now look at a typical web-service to understand the system requirements. A typical web-service has multiple service instances running on different servers. Access to these instances is via a gateway that also implements the admission control functionality. The links between the gateway and the service instances may also have significant communication cost. Moreover, each service instance maintains a waiting queue for requests.

Hence, a possible AC strategy is to apply the tail-dropping strategy at each of the service instances. To elaborate further, the admission control policy would then be based on the queue length of the service instance I and implemented by the service instance instead of the gateway. This is a natural extension to the tail-dropping strategy that is employed in the existing web-servers. A more refined strategy could be based on Chen et al.'s work [2] by using the estimated system capacity needed by the queued requests. This important work presents a method to estimate the system capacity needed for the queued requests and shows that using system capacity instead of queue length leads to significant performance improvements.
However, delegating the admission control responsibility to the service instances has some significant drawbacks. Firstly, the different service instances may experience very different workloads and hence a local policy may not be globally optimal. Also, in case a request is rejected, the client receives the information much later, i.e., after it has incurred the communication cost from the gateway to the service instance and back. This cost may be insignificant in a LAN but if the instances are geographically distributed this cost would be of concern. Moreover, if bandwidth is the constrained resource, then the request uses up bandwidth between the gateway and service instance.
We are now in a position to list the additional features our AC system should have over the current systems. In order to solve the precise problem described by Eqn. 1, (i) the AC needs spare capacity information of the entire duration from the service instance, (ii) service time, reward and penalty of the request and (iii) complete information about all the other requests. To solve problem (i), the gateway requests the spare capacity information from each service instance I whenever the refresh criterion is met. The refresh criterion is true if either the gateway has forwarded k requests to I or time T has passed since the last update, where k, T are modifiable parameters. We note that spare capacity estimation is done as described in [2]. In order to solve problem (ii), the gateway contains a proxy (See Figure 1) for every service instance that would unmarshall the request to determine the reward, penalty and request parameters. In order to estimate the service time, the proxy has a Request-to-Service time Mapper(RSM) that takes as input the request parameters and returns estimated service time. To tackle problem (iii), the proxy has a predictor that estimates the arrival rate and service time distribution for requests of each kind. This estimate can be used by the algorithm in place of actual request attributes. The proxy also has an admission controller (AC) that implements the admission control algorithm. The overall design of the proxy is described in Figure 2. Note that an RSM is also needed at each service instance for spare capacity estimation over a time horizon.
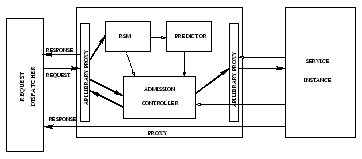
We now describe the control flow as a request r arrives. The request dispatcher forwards r to the appropriate proxy. The API proxy unmarshalls r and forwards the parameters to RSM and AC. RSM ascertains the service time from the request parameters and sends the service time associated with the request to AC. The predictor periodically sends the arrival rate and service time distribution of requests that are expected to arrive in the near future. The AC uses the above information and the spare capacity information to decide based on the methodology we describe later whether to accept the request. If the request is accepted, it is forwarded to the corresponding service instance. Otherwise, a "request rejected" response is sent to the client. Note that even though the decision to accept/reject a request is made by individual proxies, the dispatcher ensures that the workloads on different instances are similar.
We begin by distinguishing service time from response time. Service time of a request is the amount of time the resource (CPU or network bandwidth) is used by the request and not the end-to-end delay, which is the response time. Estimating the end-to-end response time for a web request to a reasonable accuracy is difficult, given the unreliable nature of the web. However, service time does not depend on the network delays and hence is unaffected by the nature of the web. We use the following method to estimate the service time of a multi-threaded web-service. For each thread which serves a request, a log is generated with the following information: 1) service parameters, 2) start time of the request and 3) end time of the request. A large number of diverse requests are sent to the web-service and enough logs are generated to make the data statistically reliable. Once the logs are generated, the service time distribution is computed for each value of the service parameters. The method is general enough to be used for the service time estimation for any other types of web-service implementations as well.
For any system, measured service time would then be a statistical function of request parameters and would be represented as Pt(t|[^v]) which is the conditional probability that serviceTime = t given that request parameter vector [^V] = [^v]. The service for which our admission control system was built is a content-based publish/subscribe (pub/sub) messaging middleware [18]. Our experiments showed that the service time of the pub/sub service for any fixed number of attributes was Gaussian with the mean of the distribution linearly related to the number of attributes.
The predictor makes a short-term forecast of arrival time distribution and service time distribution. It uses time-series analysis based short-term prediction for requests' arrival rate (ltot) as proposed in [1,2,14]. In practice, aggregated web traffic in short observation time windows is observed to be Poisson [1,17], i.e.,
| (2) |
The predictor also computes the distribution of the request attribute values (P([^v])), based on past usage. It then uses these to compute the arrival rate (l[^v]) for each distinct parameter value vector([^v]) as
| (3) |
P([^v]) for a publish-subscribe messaging utility [18] is observed to have a unique distribution. The number of attributes in a message is spread almost uniformly with small number of attributes (typically less than five) but decreases exponentially for larger numbers. The predictor uses the parameter to service time mapping Pt(t|[^v]) generated by the request to service time mapper and computes Ps(t) (probability that a request would have service time t) according to
| (4) |
The service time distribution Ps(t) for the pub/sub messaging service [18] has a body, with a uniform distribution, and a tail, which follows a negative exponential distribution. The distribution was estimated using Q.Q plot and confirmed by the Chi Square test. However, it has been observed that the service time of web-traffic follows heavy tailed distribution. This property is surprisingly ubiquitous in the Web; it has been noted in the sizes of files requested by clients, the lengths of network connections, and files stored on servers [20,21]. By heavy tails we mean that the tail of the empirical distribution function declines like a power law with exponent less than 2. i.e, if a random variable X follows a heavy-tailed distribution, then P [X > x] ~ x-a, 0 < a < 2 where f(x) ~ a(x) means that limx ® ¥ f(x)/a(x) = c, for some positive constant c. Hence, any practical admission control system should be able to perform well with a heavy-tailed service time distribution as well.
In this Section, we propose short-term prediction based AC algorithms for maximizing profit of the providers. We present a provably optimal offline algorithm for a special case of profit maximization problem in Section 3.1 and then extend it for the general case. The challenge in designing the algorithm is to come up with a practical solution. Since the number of requests n is very large, the algorithm for deciding whether a request r should be serviced, needs to be independent of n. Hence, we need a constant time algorithm for the NP-hard problem of deciding whether or not a request r should be serviced. Moreover, the problem has to be solved in an online setting.
We now simplify the maximization problem described by Eqn. 1
and find an offline solution to the simplified problem.
We fix all the rewards and penalty as
unity. Also, we assume that the reponseTimeBound bi is
kept the same as serviceTime si for each request i.
Hence, Eqn. 1 reduces to
| (5) |
With complete information at hand, it is natural to service short jobs first(SJF). We, instead, use the shortest remaining time first that combines the idea of selecting a job, which is short and has fewer conflicting requests, and is used in operating system domain to minimize waiting time [16]. As we work with non-preemptive requests we refer to SRTF as Shortest Remaining Job First (SRJF) to avoid any confusion. The only difference of SRJF from SJF in this context is that the conflict set is restricted to the set of undecided requests, i.e., the requests which have neither been rejected nor serviced. The input to the algorithm is a list of requests, which we call undecided list and the output is a service list and a reject list.
 |
 |
| (a) | (b) |
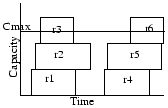
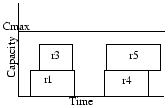
For example, assume the input request set is as shown in Figure 3(a), and the SRJF policy is followed. We take requests in an order, sorted by arrivalTime, i.e. r1, r2, r3, r4, r5, r6. We consider r1 first. Note that the only conflicting request with a shorter remaining time than r1 is r3. Also, even after servicing r3, we have spare capacity left for servicing r1. Hence, we accept r1. We then consider r2 and reject it because in the capacity left after serving r1, we cannot service both r2 and r3. By the shorter remaining time criterion r3 is preferred over r2. Hence, we reject r2 and serve r3. In the second set of requests again r4 is selected by a similar argument. But between r5 and r6, although r6 is shorter it ends after r5, and so r5 is selected. The output of the SRJF algorithm is given in Figure 3(b).
Definition 1
Shortest Remaining Job First Algorithm:
We order the requests in order of their arrival. Then we service a request
ri if we have capacity left for ri after reserving capacity for
all the undecided requests rj, s.t. aj + sj £ ai + si,
Otherwise, we reject ri.
We note that once we have taken a request from the undecided list, we either accept it or reject it. It does not go back to the undecided list.
Definition 2 Define the conflict set of request i at time t (Cit) to be the set of all such requests rj that have been not been rejected till time t and either (a) ai + si > aj and ai + si < aj + sj or (b) aj + sj > ai and ai + si > aj + sj.
We now prove the central lemma of this Section.
Lemma 1 If SRJF rejects a request rj in favor of ri at time t, then Cit Èi Í Cjt Èj.
Proof : Note that since SRJF rejects rj in favour of ri, we have ai + si < aj + sj. Let us assume there exists a request rk s.t. rk Î (Cit - Cjt). Also, since ai + si < aj + sj, if case (a) is true for rk to be in Cit, then aj + sj < ak + sk and we have ai + si < ak + sk. Similarly, if rk is not in Cjt by Case (a), i.e., we have ak > aj + sj, then ak > ai + si. So, rk is either in both Cjt and Cit or in none. Now we look at Case (b). Since, rk is in cit, we have ai < ak + sk . Also, since rk is not in Cjt, we have ak + sk < aj, i.e., ai < ak + sk < aj. Also, since rk is in the active set at time t, we also have ak + sk > aj. Hence, we have a contradiction. Therefore no such rk can exist.
Theorem 1 If the capacity of the resource is unity, SRJF maximizes the total number of serviced requests.
Proof : Let us assume the optimal services a set O of requests and SRJF services a set S. Then "rj Î O-S $rj¢ Î S s.t. SRJF had accepted rj¢ in favour of rj. By Lemma 1, we have Cj¢t Èj¢ Í Cjt Èj. Also, since rj is rejected in favour of rj¢, we have rj¢ Î Cjt. Hence, we have rj¢ Î S - O, as it conflicts with rj and so rj Ï O. We now show that for any other rk Î O - S, the corresponding rk¢ ¹ rj¢. This follows from the fact that rk Ï Cjt Èj and Cj¢t Èj¢ Í Cjt Èj and hence, rk Ï Cj¢t Èj¢. Note that ra Î Cbt ==> rb Î Cat and hence "ri Î Cj¢t Èj¢: ri Ï Ckt Èk. Also, since Ck¢t Èk¢ Í Ckt Èk, we have "ri Î Cj¢t Èj¢: ri Ï Ck¢t Èk¢, i.e., rj¢ ¹ rk¢. Hence, "rj Î O - S, $ distinct ri Î S - O hence, we have |O-S| £ |S-O|, i.e., |S| ³ |O|, and as |O| ³ |S|, we have | O| = |S|
Theorem 2 SRJF maximizes the number of serviced requests for any capacity n.
Proof :(sketch): Theorem 1 can be naturally extended from capacity 1 to n. It can be shown on similar lines that for every request rj Î O - S there exists n requests in S. Now all these (n+1) requests cannot be serviced and optimal rejects at least one of the requests, i.e., for every request rj Î O - S there exists a request rj¢ Î S - O. An argument similar to Theorem 1 using Lemma 1 shows that rj¢ = rk¢ only if rj = rk.
The offline algorithm described above needs a priori information about a request's arrival and service time. Such information is, however, not available in a real admission control scenario. Also, the requests have a QoS bound on the response time and can be delayed only till the QoS bound is violated.
Hence, short-term prediction of requests' arrival rate and service time distribution is utilized to solve the request maximization problem in a practical online setting. Note that we can compute the service time of a request as well as the service time distribution using Eqn. 4. Also, the request arrival rate to a web service can be modeled as a distribution [1,14](e.g., Poisson for web-traffic). No assumption is made about the type of distribution or its persistence in this paper.
Since the Shortest Remaining Job First (SRJF) algorithm takes requests sorted on their arrival times, it is easily transformed as an online algorithm. Our online SRJF algorithm then works in the following way. When a request arrives, it is checked whether this request can be serviced, given that the expected number of future requests which are expected to end before it are serviced. To illustrate further, if a request arrives at time t and has a service time of ten, we find the expected number of requests which will arrive at either of (t+1), (t+2,) .., (t+9) and end before (t+10), i.e., all those requests which are expected to be serviced before the current request ends. This ensures that we maximize the total number of requests serviced in an expected sense, i.e., if the assumed distribution is an exact set of requests, we should be maximizing the number of requests serviced. Moreover, if the request cannot be serviced immediately, the condition is rechecked after a rejection till such a time that the response time bound may be violated. To illustrate further, if a request with ai=T, si = 10 and bi=20 can not be serviced immediately by the SRJF criteria, it gets re-evaluated till time (T+10), after which it is finally rejected. The pseudo-code of the algorithm is presented below.
We define
L = the mean capacity of the requests,
Pr(i) = probability of event i happening.
E = random request with all parameters associated with the respective random variables
r = discount ratio
| 1 | function schedule |
| 2 | for every element j in the available array A[1...d] |
| 3 | futureRequests[j]=L * Pr(sE £ (d - j)) |
| 4 | backlog = 0 |
| 5 | for k = 1 to j |
| 6 | backlog = backlog + |
| futureRequests[k]* Pr(sE ³ (j-k)) | |
| 7 | end-for |
| 8 | capacityLeft = available[j] - |
| r* (backlog + futureRequests[j]) | |
| 9 | if(capacityLeft £ 1) |
| 10 | return false |
| 11 | end-if |
| 12 | end-for |
| 13 | return true |
| 14 | end function |
The discount ratio r served two purposes. It captures the confidence in the prediction as well as a future discounting ratio. A predictor with a high error probability would have a r much less than 1 as the estimation of futureRequests may be off margin. On the other hand, a sophisticated predictor would have r® 1. For actual service deployment, the service provider should start with a default value of r depending on the predictor used and converge to the value optimal for her. Note also that in case a request r is rejected by schedule once, it is recalled till such a time when the QoS bound on the request r cannot be satisfied, if it is delayed any further.
Our algorithm for the general case of Profit Maximization (i.e., one in which all rewards and penalties are not equal) is based on the following lemma about optimal O.
Lemma 2
If for any request ri, $C¢i Í Cit s.t.(i) "rj Î C¢i (a) Cjt ÇC¢i = f, (b) aj + sj < ai + si, (c) rj Ï O
(ii) årj Î C¢i Rj + Pj > Ri + Pi, then ri Ï O.
Proof :(sketch) Let us assume that such an ri exists and belongs to optimal O. Let us define C¢i = Èrj Î C¢i Cjt. By a simple analysis for each element of C¢i on the lines of the proof of lemma 1, one can show that C¢i Í Cit. Hence, we can replace ri by C¢i in O and the overall profit would be increased. Hence, we achieve a contradiction.
Hence, our offline algorithm (offline BSRJF) essentially rejects all such requests ri for which C¢i exists. It finds out all the candidate C¢i for each ri and pre-reserves capacity for them. If spare capacity is left after pre-reservation, then ri is serviced. This essentially leads to the following theorem about offline BSRJF.
Theorem 3 If offline BSRJF returns a set BS of requests, then "S s.t |BS - S| £ 1, the total revenue generated by BS is more than that generated by S.
Proof : The proof follows directly from Lemma 2 and the fact that BSRJF constructs BS s.t. "ri Î BS, there does not exist C¢i
In the online version of BSRJF, we compute the expected sum of reward and penalties for such C¢i candidates, i.e., we compute the sum of the expected rewards and penalties of non-conflicting request sets rS that arrive later. We compare this sum with the reward of the current request under consideration. If the sum of the expected rewards and the penalties saved exceeds the reward of the current request, we reserve capacity for rS. This ensures that ri is serviced only if there is no expected C¢i that would be rejected later.
This is incorporated by changing Line 3 of the online SRJF algorithm by
| 3 | futureRequests[j] = L* | åi=1d-j (Pr(sE = i)* f(d,i,j)); |
|
Note that now capacity is not reserved for all earlier ending requests but only those who belong to a such a set C¢i. The algorithm in the offline scenario no longer guarantees an optimal solution but a solution that in some sense is locally optimal. This is because there is no single request ri that can be replaced from the solution by some Ci¢ and the solution would improve. However, there may exist a set of such ri's that could be removed and the objective function (Eqn. 1) may increase.
We take an example to explain the difference of
this algorithm from online SRJF.
If a request ri of length 10 which starts at time-unit 50 and has
successfully passed up to 55th time-unit by the algorithm and there is a
conflict with a request rj, which spans from 55-58, we may choose ri
if the probability of a request of length two (which can fit in 58-60)
times the penalty of one request is less than the difference in
net reward of ri and rj.
More precisely, resource is not reserved for rj in favor of ri if
for an expected request k:
| (6) |
Herein, a request of larger length ri is admitted which may disallow an expected shorter request rj later but the probability that there would be another request rk in the remaining time is very low, i.e., expected sum of rewards and penalties of C¢i = rj Èrk is less than Ri + Pi. One may note that within this formulation online SRJF can be thought of as representing capacity for all such candidate C¢i irrespective of the revenue generated by C¢i. We now explain BSRJF's behaviour when the requests are from multiple SLA classes.
Multiple SLA Classes: When a choice has to be made between requests from the same class, BSRJF chooses the one that has a shorter remaining time. However, when a choice is to be made between requests of different SLA classes, the actual measure implicitly used is reward per unit capacity consumed. Note that a request of low reward class would have f(d,i,j) = 1 for all the expected requests of higher classes, i.e., it would be rejected in favor of any shorter request of the higher priority classes irrespective of the fact that there may not be any chance of scheduling an extra request. On the other hand, assuming zero penalty, a high priority request can be rejected in favor of low priority requests only if it is longer than the reward ratio of the two SLA classes times the expected service time of the low priority requests, i.e., in a zero penalty scenario, where a request of Gold class has a reward three times the reward of a Silver class request, we would reject the gold request only if we expect to service three disjoint silver requests in the same time.
We now assess the overhead we have to incur for having an elaborate admission controller. For any client server system, a server thread would accept a request and add it to a service queue. Also, even a simple tail-dropping admission controller would have to look at the queue to determine its length and decide if the incoming request has to be dropped. Hence, the cost of admission control is at least O(1) for every request which has arrived at the AC. Note also that in case the request is accepted, we have to add the request to the queue, which would imply scanning the whole request which is O(l), where l = length of the encoding of the request. Hence, the running time per request is O(l).
In our AC system, we parse the headers of all requests to determine its parameters. Once the parsing is done, the AC algorithm works only with an array (available array of length equal to the short-term forecast T), which is representative of the actual queue. Also, T can be suitably replaced by any constant k that is equal to the number of time-instances of T (values taken by j in the pseudo-code) at which we want to check the AC condition, e.g., if T = 100 and we make k=10 equal sized partitions, we collapse all the entries between 10 i+j, 0 < j < 10 into a single entry corresponding to the ith partition. One may reduce the number of points (in time) that one would check the AC condition for, to account for the fact that the load at different points would follow temporal correlation. Hence, if the AC condition is satisfied at a time t in the horizon, with high probability it would also satisfy in the temporal neighbourhood of t. This would bring the overhead even lower and could be assumed to be constant. Thus effectively the running time is O(l) per request, which is the same as a tail-dropping AC system.
We conducted a large number of experiments with a hosted content-based
publish-subscribe messaging middleware service [18].
Our experiments compare
the performance of our SRJF-based algorithms to the following predictable
service time-based
AC algorithm.
Greedy:
The greedy heuristic computes the expected system load over a time horizon by estimating the service time
of all the requests which have been accepted (i.e., which are in the service
queue). It accepts a request R,
if there is spare capacity
available to service R. Note that this heuristic is superior
to the tail-dropping strategy, used by current web-servers. This is because greedy directly uses the system load information,
whereas, tail-dropping systems use queue-length as an approximation of the system load.
Performance numbers obtained in our experiments clearly establish the effectiveness of SRJF-based
policies for admission control over greedy and, by extension, over tail-dropping as well.
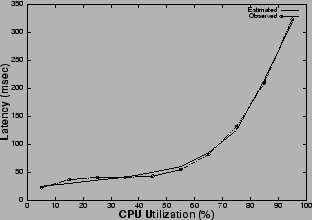
The publish/subscribe messaging service [18] under consideration supports a programmatic interface, based on the standard Java Messaging Service (JMS) API, and allows for attribute-based subscription of published messages. One key QoS parameter for a pub/sub messaging service [18] is the latency of a message, i.e., the time a message takes to reach a subscriber from a publisher via the messaging broker assuming zero network delay. The latency for a message is observed to vary with the CPU utilization of the broker in a manner, described in Figure 4. Hence, to ensure an upper bound on the latency guarantee as per the SLA, the CPU load should be kept below the threshold value. This places a limitation on the number of requests which can be serviced, as allowing any more requests would load the CPU above the threshold value and violate the latency bound resulting in losses for the publish/subscribe service provider. Thus, we can view the CPU as a resource which has a capacity equal to the threshold value which limits the number of concurrent requests. We instrumented the messaging service to obtain a performance model, and to determine the CPU thresholds to satisfy the QoS guarantees and the corresponding limit on the number of concurrent requests (Figures 4, 5), which is the capacity of the service.
The experiments simulate a request driven server model that hosts a publish-subscribe messaging service using empirical workload from the distributions generated as described in Section 2.3.2. The traffic arrival was modeled as a Poisson process. Reward was proportional to the service time of the request and penalty was proportional to the average service time (Section 2.2). We used two service time distributions for our experiments. Firstly, we used the service time distribution unique to the messaging service, i.e., with an exponential tail. We also conducted simulations with a heavy-tail replacing the exponential tail to study the performance in other service time scenarios. Since we had no heavy-tailed data for the publish-subscribe messaging service, we used traces from Internet Traffic Archive. The trace used consisted of all the requests made in a one week to the Clarknet WWW server [22]. The service time distribution of the above trace fitted a log-normal distribution, which is heavy-tailed. For our experiments, the service time distribution was scaled to have a mean of 1000 ms. Each experiment was repeated until statistical stability was achieved and the computed means are reported.
We conducted experiments in the single and multiple SLA class settings. The performance improvement of our algorithms with multiple SLA classes is more significant than with single SLA class. Moreover, the performance improvement can be arbitrarily increased by increasing the reward ratio of the classes. The reason for this lies in the fact that Greedy is class blind. However, the significant performance improvement over Greedy that we achieve in a single SLA class scenario establishes that our algorithms do not depend on the reward ratio to achieve a superior performance. We would also like to note that these results are also valid if the competing algorithm is a proportionate greedy algorithm, one where a proportionate share of the resource is alloted to each class and that share is consumed greedily by the requests of that class, as the admission control algorithm for each of the partition of the resource could be interpreted as a greedy algorithm in isolation.
In Section 4.2, we report the performance of our algorithms against the greedy with varying inter-arrival delay, i.e., the request arrival rate decreases along the x-axis. In the second set of experiments we keep the arrival rates and mean service time constant and increase the variation in service time, which we call spread. The mean of the service time was fixed at 1 ms.
We observed that greedy performs worse when the tail is heavy as compared to a exponential tail. This can be attributed to the fact that the long requests become more frequent. However, our algorithms seem to show no adverse effect because of the heavy tail (Figures 9, 10). This is not surprising as our algorithms prune out the long requests even if they are more frequent. For lack of space, we report the full results with the exponential tail only and note that the improvement with a heavy tail is more significant (Figures 9, 10).
The results show (Figures 6, 8) that when the resource is in plenty (i.e., at low arrival rates or large inter-arrival delay), greedy performs as good as SRJF and BSRJF algorithm. This is expected because the requests are rejected very rarely, as at most times, spare capacity is available. However, as the request arrival-rate increases, the intelligent algorithms consistently beat the greedy heuristic by a large margin. In fact, we observe that the total number of requests serviced are more than doubled at a high request rate (low inter-arrival delay). These indicate that, as the number of admission control decisions increase, the performance improvement of our algorithm over greedy increases, emphasizing their superiority over greedy at heavy load. We note that BSRJF services approximately the same number of requests as SRJF. However, we note that the reward obtained by SRJF is less than BSRJF (Figures 6, 7). Hence, BSRJF gets a significant increase in rewards with only a small increase in penalty as compared to SRJF, thus increasing the revenue considerably.
The rewards obtained by the three heuristics implicitly contain the information about the capacity utilization by the heuristics. This is because reward is proportional to the service time of the request in the model used for these experiments. Hence, the sum of all the rewards obtained is directly proportional to the total system capacity used by all the serviced requests. It is also easy to see that the rewards obtained by the greedy is a good approximation for the total capacity in high load scenarios as greedy will almost always fully utilize the resource. In a low load scenario as well, the rewards obtained by greedy equal the maximum resource utilization as almost all the requests are serviced. Thus, Figure 7 shows how well the two heuristics consume the resource compared to greedy.
The number of requests serviced by our heuristics increases significantly with increase in spread as is evident from Figures 9 and 10. Since the mean service time and arrival rate are the same, the number of conflicts for resource should be comparable for all the data points. Hence, the only attribute, which increases, is the variability in the service time of the requests. As our algorithms take the service time as the most important criterion (SRJF uses it as the only criterion), the increase in variability allows our algorithm to make more intelligent decisions. This is reflected in the improved performance as opposed to greedy, which services approximately the same number of requests at all values of spread. A similar trend is visible (Figure 11) in the revenue obtained by balanced SRJF when compared with greedy. The increase in spread increases the revenue of the balanced SRJF whereas it clearly shows no effect on the performance of greedy, which is blind to service time variability.
We propose a short-term prediction based admission control methodology for profit maximization of service providers and demonstrate its effectiveness under heavy and diverse workload conditions. Our methodology is less susceptible to workload variations, observed in Internet environment, since we do not assume any specific arrival and service time distribution. Our algorithms perform considerably better than greedy if either there is sufficient resource constraint, i.e., there are many more requests than the capacity available or the service times have a larger spread. The reason for the first is that there are actually more decisions to be made if there are more conflicting requests and hence, the selected requested set could be vastly different from the set that greedy generates. The second factor is an indicator of the diversity of the requests and hence, our algorithms perform better when the workload is more diverse.
The authors would like to thank Neeran Karnik for discussions about the system design and Rahul Garg for valuable comments on earlier versions.
1Note that in this paper web service
and networked service are used
synonymously. Strictly
speaking, a web service interface describes a collection of
operations that are network accessible through
standardized XML messaging.