AT&T Labs-Research
Z. Morley Mao![]() , David Johnson,
Oliver Spatscheck, Jacobus E. van der Merwe, and Jia Wang
, David Johnson,
Oliver Spatscheck, Jacobus E. van der Merwe, and Jia Wang
AT&T Labs-Research
Copyright
is held by the author/owner(s).
WWW2003, May 20-24, 2003, Budapest, Hungary.
ACM 1-58113-680-3/03/0005.
Today, most large companies maintain virtual private networks (VPNs) to connect their remote locations into a single secure network. VPNs can be quite large covering more than 1000 locations and in most cases use standard Internet protocols and services. Such VPNs are implemented using a diverse set of technologies such as Frame Relay, MPLS, or IPSEC to achieve the goal of privacy and performance isolation from the public Internet.
Using VPNs to distribute live content has recently received tremendous interest. For example, a VPN could be used to broadcast a CEO-employee town hall meeting. To distribute this type of content economically without overloading the network, the deployment of streaming caches or splitters is most likely required.
In this paper, we address the problem of optimally placing such streaming splitters or caches to broadcast to a given set of VPN endpoints under the constraints typically found within a VPN. In particular, we introduce an efficient algorithm with complexity O(V), V being the number of routers in the VPN. This guarantees the optimal cache placement if interception is used for redirection. We prove that the general problem is NP-hard and introduce multiple heuristics for efficient and robust cache placement suitable under different constraints. At the expense of increased implementation complexity, each heuristic solution provides additional saving in the number of caches required. We evaluate proposed solutions using extensive simulations. In particular, we show our flow-based solution is very close to the optimal.
The distribution of live streaming content is gaining popularity in VPN environments to support webcasts ranging from tens to hundreds of thousands of streaming media clients. Due to a lack of layer 3 multicast availability in these environments, such streaming services are typically offered using unicast transport protocols. Obviously the inherent problem of distributing such a large number of streams via unicast delivery is that some links within the VPN might become overloaded.
The typical VPN network topology compounds this problem even further. VPNs usually consist of a small hub network which provides connectivity to, in some cases, thousands of individual spokes. The fact that both the hubs and the spokes are usually geographically distant makes increasing the bandwidth to accommodate a large number of unicast streams prohibitively expensive.
The standard solution to this problem is to deploy streaming cache servers within the VPN which in the context of live streaming simply split the unicast traffic and, therefore, can be used to offload congested links. Such cache servers are offered today by a large number of vendors such as Network Appliance, Volera, and Cisco Systems. However, the cache cost, as well as the maintenance cost associated with each cache, requires careful placement of the caches to minimize the overall cost of the live streaming infrastructure. In the context of an existing VPN, it is therefore important to find the optimal cache placement to minimize the number of caches which have to be deployed to serve a given client population.
We first show that this optimal cache placement problem is NP-hard in general, and hence only restricted versions of the problem are likely to be efficiently solvable. We then show that the problem restricted to the use of interception caches has a provable optimal solution with complexity O(V) with V being the number of routers in the VPN. We also provide heuristic solutions for the general case and thoroughly evaluate them using simulations. Each heuristic solution provides improvement over the interception-based solution at the expense of additional implementation cost.
The rest of this paper is organized as follows. In Section 2, we discuss related work. Section 3 contains a more detailed problem statement and describes our proposed cache placement algorithms. Section 4 describes the simulation method we used to evaluate the proposed algorithms, and Section 5 contains the simulation results. Section 6 concludes the paper.
While a significant body of related work exists, we believe the work presented in this paper to be unique in the following aspects:
In the Web space, several papers consider the placement of objects or replicas on network servers [6,8,7]. The purpose here is to decide which objects should be replicated on what set of network servers while trading off improved performance against the cost of servers. For the problem of live streaming, which we have addressed, this kind of partial object placement is not possible because in general all of the content (i.e., the complete live stream) needs to be distributed to all users.
Another group of papers investigated the placement of network servers in various scenarios [13,12,5,11]. The most general of these with a problem statement closest to our work is work by Shi and Turner [13]. They consider the number of servers which are needed and where they need to be placed in an overlay network to satisfy a certain quality of service to all clients. Their work differs from ours in that it aims at an Internet environment rather than the more constrained VPN environment we have considered. Furthermore, while their problem statement is very general, they make a number of simplifying assumptions, e.g., network capacity constraints are ignored, which is not realistic for our problem setting. Work by Jamin et al. [5] and Qiu et al. [12] investigate server placement in the context of performance improvement of Web traffic.
In summary, the existing cache or object placement algorithms for Web traffic in the Internet environment do not directly apply to our problem, because streaming services have a more strict requirement on bandwidth. There is usually a minimum bandwidth guarantee needed for the streaming service to be acceptable. Furthermore, streaming events are typically of longer duration than web transactions and thus sufficient bandwidth must exist between the client and the server during the entire duration of the event. By taking into account this additional and indispensable bandwidth constraint, our study is focused on developing both efficient and robust algorithms for provisioning streaming services in mostly known network settings.
Figure 1 depicts a typical VPN topology to illustrate the scenario we are considering in this paper. In the figure, a live stream is assumed to originate from an origin server which connects directly to a densely interconnected ``hub network'', consisting of high capacity (typically WAN) links. It interconnects ``spoke networks'' consisting of richly connected islands of LAN technology.
Figure 1 also shows the inherent problem with distributing continuous streaming content via unicast delivery. The thick lines show a shortest-path distribution tree from the origin server. The numbers next to each of the lines indicate the required capacity of each link assuming that each spoke network requires three units of capacity. The well-known solution to this scalability problem consist of the distribution of streaming caching servers throughout the network to effectively form an application level multicast distribution mechanism.
In this paper, we address the practical and important problem of determining the minimum number of caching servers required to deliver live unicast streaming content to a given client population. By definition, a client represents a streaming media end user that requests a single live stream. We start by assuming that the network topology and link capacities are known. These constraints are relaxed later to investigate the robustness of our algorithms. We assume all clients need to be satisfied, i.e., we want to serve the live streams without degradation in quality to all clients. Given the minimum number of caching servers, a second optimization criterion is minimizing the network congestion defined as the total bandwidth usage by placing the caches strategically.
There is an inherent tradeoff between bandwidth utilization and the number of caches needed to satisfy a user population. At an extreme, we can place a cache at each router to achieve the minimal total bandwidth usage, i.e., emulating the use of native multicast. The optimization criteria we study in this paper require that we satisfy all users with the minimal number of caches. Therefore, we first find the minimal number of caches and then place them to minimize bandwidth usage. We emphasize that our algorithms can be easily adapted to a different cost model by modifying the cost of adding caches and bandwidth usage. For instance, our algorithms can be used to discover the bottleneck links and compare the cost of placing a cache versus just upgrading the link. Our contribution is to provide a general framework for optimizing different criteria. We believe that our chosen criteria represent a reasonable choice for practical considerations.
More precisely we make the following assumptions unless otherwise stated:
As indicated earlier, we use this ``perfect'' knowledge as a starting point and then consider the robustness of our algorithms in the case of incomplete knowledge.
 |
Claim: The Minimum Cache Placement problem is NP-hard.

Note that although the topology of the instance we constructed does not follow the ``hub and spoke'' model specified in the previous section, it could be the topology for a spoke in such a model, and thus the problem remains NP-hard when restricted to the hub and spoke model. Note also that the construction in the above proof shows that the Cache Placement Problem is NP-hard even if all links are symmetric and all capacities are equal to 1. Furthermore, the result holds both when all routes must follow shortest paths as in OSPF and when there are no constraints on routing other than link capacity.
To make use of streaming caching servers to build
application level distribution trees, streaming clients have
to request the stream from a caching server rather than the
origin server. One way to achieve this is
by transparently intercepting requests for streaming content
at the network layer and passing it to a caching server, the
intercepting proxy approach, as illustrated in Figure 3.
In the figure, the numbers next to each of the lines indicate
the required capacity of each link;
arrows of the same line type indicate these streams come
from the same source ![]() .
WCCP [3] is an example protocol that enables this
functionality by intercepting requests on certain port
ranges in a router and passing all such traffic to
a caching server.
.
WCCP [3] is an example protocol that enables this
functionality by intercepting requests on certain port
ranges in a router and passing all such traffic to
a caching server.
Fortunately, when intercepting proxies are used, the problem is simplified by restricting traffic to a single distribution tree rooted at the origin server. Thus, a cache can only serve the clients downstream from the root of the tree, given the viewpoint that the root of the tree is the origin server. Such a restriction represents the mechanism used in the intercepting proxy solution where end clients are requesting from the origin server as they would normally do, but caches placed on the route between the client and server intercept the request and deliver the stream. We now present a simple and efficient greedy algorithm that gives the optimal solution in terms of the minimum number of caches. We subsequently show how a dynamic programming algorithm working on the results of the greedy solution can compute a way to place this minimum number of caches so as to minimize the total bandwidth used.
We assume we are given a distribution tree T with nodes V and edges E
directed away from the root vs, which is the origin server for the stream.
In addition, there is a capacity Ce for each edge ![]() ,
and a demand (number of clients requesting streams) Sv for each node.
We assume without loss of generality that every leaf node has
at least one client requesting a stream, i.e., that
,
and a demand (number of clients requesting streams) Sv for each node.
We assume without loss of generality that every leaf node has
at least one client requesting a stream, i.e., that ![]() for
all leaf nodes v. If not, we can simply delete the leaf node and its
incoming link from the tree.
The tree itself can be computed in O(|V|) time based on router table
information, assuming that shortest path routing without path splitting is
in effect, as in common implementations of the OSPF routing protocol.
for
all leaf nodes v. If not, we can simply delete the leaf node and its
incoming link from the tree.
The tree itself can be computed in O(|V|) time based on router table
information, assuming that shortest path routing without path splitting is
in effect, as in common implementations of the OSPF routing protocol.
In what follows, we shall use the notation De to denote the amount of
bandwidth required on link e, given the current cache placement.
Note that if De > Ce the link is overloaded. If the link
(u,v) is overloaded, we shall call v a red node; otherwise
it is a green node.
Note that one way to get a feasible cache placement is simply to identify
the set of red nodes for the case of no caches, and then place a cache on
each red node. This will be called the ``red nodes'' solution in what
follows. This may not be an optimal solution however. To get an optimal
solution for a tree T, we can use the following algorithm.
Algorithm:
Label each node v with a depth value d(v) - the number of links on
the path from v to the origin server vs.
Let
![]() .
For each node v, let e(v) denote the incoming link for v, i.e.,
the unique edge (u,v) in the tree.
(We can let this be a dummy edge of infinite capacity in the case of the
root vs.)
Let T(v) denote the subtree rooted
at v and let children(v) denote the set of nodes u such
that
.
For each node v, let e(v) denote the incoming link for v, i.e.,
the unique edge (u,v) in the tree.
(We can let this be a dummy edge of infinite capacity in the case of the
root vs.)
Let T(v) denote the subtree rooted
at v and let children(v) denote the set of nodes u such
that ![]() .
.
Greedy(T)
For each i=(dmax, dmax-1, .... 1),
For eachwith d(v) = i
Recompute De(v) as.
If De(v) > Ce(v), place a cache at v and set De(v)=1.
Note that the algorithm works in from the leaves of the tree, processing a node only after all its children have been processed. It takes time O(|V|) since it processes each node once, and looks at each link (of which there are only |V|-1 in a tree) just twice.
Claim: The greedy algorithm assigns the minimum number of caches
needed to satisfy all client requests, assuming flows are restricted to
the distribution tree T.

As shown in the previous section, the greedy algorithm produces a cache placement for a tree such that for any node in the tree, the number of caches in the subtree rooted at the node is the minimum possible if all requests in that subtree are to be satisfied. This placement may not, however, be the best with respect to bandwidth utilization of some other measure of congestion. A standard method for measuring overall congestion is to take the sum over all edges e of a congestion cost cc(e,t) for that edge, where t is the amount of traffic carried by edge e, and cc(e,t) is typically assumed to be a nondecreasing function of t. For this application, we may assume that t is an integer in the range from 0 to capacity(e), where capacity is expressed in terms of the maximum number of simultaneous streams the link can carry. For congestion cost corresponding to bandwidth utilization is simply cc(e,t) = t.
It is not difficult to see that it might be possible to decrease total congestion cost by moving a cache from its greedy location toward a leaf. Although this may increase the traffic on the link coming into the old location, it might decrease the traffic on the link between the old and the new location, for a net decrease in congestion.
In this section we observe that, given the greedy placement and an
arbitrary congestion cost function cc(e,t), we can efficiently
find a placement that minimizes total congestion cost, subject to the
constraint that the optimal number of caches must be used.
The algorithm uses dynamic programming and takes time
![]() .
Note that this can be fairly expensive, since some of the links in the
cores of the networks we study in our simulations have sufficient capacities
to carry more than 8000 streams.
However, one would expect a shortest-path tree in such a network to contain
relatively few such edges.
.
Note that this can be fairly expensive, since some of the links in the
cores of the networks we study in our simulations have sufficient capacities
to carry more than 8000 streams.
However, one would expect a shortest-path tree in such a network to contain
relatively few such edges.
Preliminary simulations show that applying the algorithm
to the bandwidth utilization case (cc(e,t)=t)
can result in improvements of as much as
![]() in total congestion for large topologies. The technical
details of the algorithm and the simulations will be presented in the
extended version of this paper.
in total congestion for large topologies. The technical
details of the algorithm and the simulations will be presented in the
extended version of this paper.
In the previous section, we assumed that client requests are intercepted on layer 3 and redirected to an appropriate cache. However, all cache vendors today offer in addition to interception based redirection, layer 7 based redirection methods such as DNS, HTTP/RTSP redirect or meta-file rewriting [2].
Layer 7 redirection relaxes the constraint of using a single distribution tree from the origin server and allows each client to use any cache, no longer restricting the client to caches that lie between it and the root on a fixed distribution tree. Since this problem is NP-hard as proved in Section 3.2, we settle for designing heuristics that attempt to find near-optimal solutions.
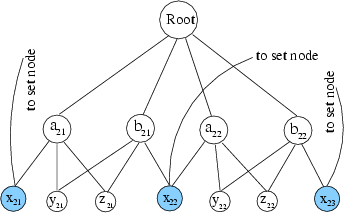
Similar to the Content Distribution Networks that commonly use DNS to do server selection [10], a layer of indirection is required to translate the request for streaming server by the user to the desired server. Such Layer 7 redirection can be done at different granularities with higher cost associated with a finer granularity. At the extreme, each client attached to the router can potentially select a different cache server. A more coarse-grained redirection can be done on a per prefix level. Similarly, clients attached to the same router are constrained to select the same server. We consider the improvement in cache reduction compared to the greedy algorithm at two different granularities: client-based redirection and router-based redirection. Note, due to the inherent tradeoff between bandwidth usage and the number of caches, these solutions attempt to find fewer caches by making use of links with spare bandwidth and hence have higher overall bandwidth utilization. These two approaches are shown in Figures 4 and 5. In Figure 4, all clients connecting through the lower left router are served from the same cache, while in Figure 5, clients connecting through the bottom left router are served from two different caches. Here we assume the two clouds attached to the lower left router are not separate spoke networks; they are clients directly connected to the router.
Greedy_Router_Redirect(G,T)
Begin by computing link demands De under the assumption that
all routing follows the distribution tree and no caches are used.
Let R denote the initial set of red nodes (nodes v whose incoming
link e(v) has De(v) > Ce(v)).
For each i=(dmax, dmax-1, .... 1)
Letbe the set of red nodes with d(v)=i.
For each,
Call heuristic H(v) (described below) to identify
a set R(v) of red nodes that can be turned green if
a cache is placed on v. Set x(v)=|R(v)|.
Order the nodes in R' by decreasing value of x(v).
While R' is nonempty,
Let v' be the first node in R' according to the above order
and place a cache at v'.
To the extent possible use the routing computed by H(v')
to turn red nodes in R(v') green, so long as this can be
done without turning any green nodes red.
(Note that if this is not the first cache placed at depth i
not all conversions envisioned in the computation of H(v)
may still be possible.)
Remove any nodes that have turned green from R and R'.
The heuristic H(v) works as follows. We randomly pick nodes (without replacement) from R in order of decreasing depth, starting with depth d(v). (By the way the algorithm works, H(v) is only called when there are no red nodes with greater depth than v.) For each chosen node v', we then look for a way to route streams from a cache at v to v' or its children so as to reduce the demand on e(v') enough to turn v' green, subject to the requirement that if the cache serves any client at a node, it must serve all the clients at that node. If we find a way to turn v' green, we adjust the traffic on the affected links to reflect the changes required, both from adding the new streams from the cache at v and from deleting the old streams from other caches or the origin that were replaced. We then go on to the next choice for v' and continue until we have considered all red nodes other than v.
Note that H is just a heuristic. (The problem of finding the maximum number of red nodes that can be turned green is itself NP-hard.) As we have implemented it, H has running time O(|V||E|), so the running time for the overall algorithm is O(|V|2|E|).
Thus, it is essential to evaluate how well our algorithms perform
under such practical constraints. The solutions presented so far
unrealistically assume that the link capacity is well known and there
is no background traffic. In Section 5 we empirically measure
the number of clients left unserved due to faulty capacity estimation
in our model, and also measure the improvement obtainable if we restrict
usage of links to ![]() of capacity, thus using more caches but hopefully
serving more clients.
of capacity, thus using more caches but hopefully
serving more clients.
To evaluate the effectiveness of various algorithms proposed in this paper, we simulate the behavior of our algorithms on typical VPN hub-spoke topologies. In this section, we discuss the simulation parameters and assumptions, network topologies, and evaluation metrics used.
Our simulations encompass three classes of VPNs.
We modified the GT-ITM internetwork topology generator [1] to produce layer 3 hub-spoke topologies. Since each router has a number of clients requesting the streaming service, we make sure that the topology is connected. The topology inside each spoke domain is constructed by connecting two vertices randomly with a specified probability.
The input parameters to the topology generator are the following: number of fully meshed hub routers, average number of spoke domains per hub router, average number of routers per hub, number of multihoming links, and the probability that two routers inside the same spoke are connected. Multihoming links are randomly placed between a hub router and a spoke router not within the spoke domain connected to the hub router. Furthermore, for the evaluation of the resilience of our algorithms to uncertainties in topology data, the topology generator also takes in an error distribution for link capacity estimation and a value representing the probability that two links in the same spoke domain share at layer 2.
|
|
We first study the effectiveness of our greedy algorithm. We also highlight some interesting effect of the topology on the cache requirement. Figure 6 plots the average number of cache servers per router required using the greedy algorithm for spoke router degree of 3 and 4, as the spoke domain size increases. The size of hub network is fixed at 5 hub routers, each with an average of 40 spoke domains. We define the spoke router degree or spoke degree to be the average number of outgoing links a router in the spoke domain has. The figure shows that increasing spoke domain size increases the overall cache requirement and increasing spoke router degree decreases cache requirement. With larger spoke domain size, there is inherently higher demand for bandwidth because of larger number of clients. However, the average number of caches per router actually decreases slightly with increasing spoke size, because a single cache can serve more clients. With higher router degree, a cache placed inside a spoke domain can serve more clients; therefore, fewer caches are needed overall. Intuitively, caches should be placed where there is high degree of connectivity to maximize its benefit.
Figure 6 also plots the number red nodes versus topology
size. Red nodes are routers with demand from child
routers exceeding its parent link capacity in the original
distribution tree before any caches have been placed. This gives an
upper bound on the number of caches required using the greedy
algorithm. As the number of routers increases, the probability of a
cache alleviating the demand of its parent red nodes also increases.
Note that the percentage by which the greedy algorithm improves on this
upper bound is substantial, although the gain declines as router
degree increases. For large topologies with spoke degree of 3, the
maximum reduction in cache requirement is about ![]() .
The variance in the results are due to differences in the number of
multihoming links, client distribution, and randomness in topology
generation.
.
The variance in the results are due to differences in the number of
multihoming links, client distribution, and randomness in topology
generation.
We now study the benefit of caching on reducing bandwidth usage. Figure 7 plots the average per link bandwidth requirement in the presence of caches using the greedy placement (shown in Figure 6) compared with that in the original network using a distribution from the origin server. The benefit of cache servers is quite clear, as the bandwidth requirement grows roughly sublinearly with the greedy algorithm's cache placement. The rate of increase is visibly faster in the case when no caches are present. We also note that the original bandwidth requirement for the topology with spoke router degree of 3 is slightly higher than the topology with spoke router degree of 4 for the same router count. Intuitively, with higher spoke degree, there is higher chance of aggregating traffic because the distribution tree is bushier. With higher router degree, a single cache also has more chance of serving more clients. As we have shown in Figure 6, fewer cache servers are needed with higher spoke degree for the same topology size. Due to the inherent tradeoff between the number of cache servers and bandwidth usage, the bandwidth usage in the presence of caches is slightly higher for the topology with spoke router degree of 4, because of fewer number of caches.
Figure 8 shows the median number of caches required for a given topology as the number of multihoming links increases. The topology consists of 12 hub routers with an average of 10 spoke domains per hub router and a spoke router degree of 3. On average, there is less requirement for cache servers as the number of multihoming links increases. Any multihomed spoke domain can reach the hub network through any of the links. The shortest path tree rooted at the origin server in the hub network takes advantage of such multihomed links to find higher capacity paths to the spokes and thus minimize the number of caches needed. In this example shown, for this particular topology, the amount of saving in the number of cache server requirement can be more than
Figure 9 shows the effect of the number of spokes per hub node or the spoke size on cache requirement. In this set of simulations we keep the total number of routers in the topology constant at 2,412; the total number of clients varies between 105,486 and 109,072 with standard deviation of 694. There are 12 hub nodes in the hub network. We vary the number of spoke domains attached to each hub router. In effect, we also vary the number of routers in each spoke domain to keep the total number of routers constant. At one extreme, each hub router has only a single spoke domain with 200 routers. At the other extreme, each hub router has 200 spoke domains, each with a single router. As the number of spoke domain increases, less aggregation is possible. Each spoke domain only has a single link to the hub domain. If that link is unable to support the client demand within the spoke domain, a cache must be placed there. The smaller the spoke domain, the fewer clients can make use of the cache. As a result, the topologies with numerous small spoke domains require significantly more caches. We emphasize that this is an inherent limitation in the topology and is not due to the greedy algorithm. Designers of VPNs may take this effect of topology on cache requirement into consideration.
We now compare the greedy algorithm and the additional redirection
systems with the bound obtained using local exhaustive
search. Figure 10 plots the average number of caches
per router with each data point representing the mean of 60 simulation
runs with varying number of multihoming links.
It shows that as the number of routers
increases, greedy is outperformed by router-based, client-based,
and flow-based redirection. With large topologies, client-based redirection can
reduce the number of caches used by greedy algorithm by more than ![]() .
We also observe that finer grained redirection provides
sufficient benefit for large networks. Client-based redirection can
provide more than
.
We also observe that finer grained redirection provides
sufficient benefit for large networks. Client-based redirection can
provide more than ![]() in the number of caches compared
with router-based redirection. And flow-based redirection can in
addition reduce up to
in the number of caches compared
with router-based redirection. And flow-based redirection can in
addition reduce up to ![]() number of caches compared to the
client-based redirection. The curve for flow-based algorithm and local
exhaustive search are very close to each other, indicating that
flow-based redirection results in close to optimal number of
caches. In fact, the difference is just 18 caches or less for large
topologies, out of a total of 384 or fewer caches.
number of caches compared to the
client-based redirection. The curve for flow-based algorithm and local
exhaustive search are very close to each other, indicating that
flow-based redirection results in close to optimal number of
caches. In fact, the difference is just 18 caches or less for large
topologies, out of a total of 384 or fewer caches.
This particular example is based on the network topology consisting of 6 fully meshed hub routers in the hub network, each hub router having on average 20 spoke domains, and an average spoke router degree of 3. The number of multihoming links vary between 1 and the hub size 6. This means that the local exhaustive search may predict up to 6 fewer caches compared to the true optimal placement. We have observed similar results with different topology setups.
Figure 11 plots the number of unsatisfied users due to overloaded links for each algorithm when we introduce an empirical error distribution for link capacity values from our measurement study and
One possible way to deal with the imperfect topology information is to
always leave some spare bandwidth on each link or on links where we
suspect our capacity estimation is incorrect. We implemented
this heuristic and only let our algorithms use ![]() of
the estimated link capacity. Note that underestimating the link capacity
will result in more caches being used, in this case roughly
of
the estimated link capacity. Note that underestimating the link capacity
will result in more caches being used, in this case roughly ![]() more.
On the other hand, the number of unsatisfied users, while continuing
to grow with topology size, is substantially reduced, as can be
observed in Figure 12.
Our evaluation also makes a compelling case that
we need measurement information or external knowledge
on where links are most likely shared and where capacity estimates are
not accurate. Given such information, we can selectively avoid
overloading these links in the algorithms.
more.
On the other hand, the number of unsatisfied users, while continuing
to grow with topology size, is substantially reduced, as can be
observed in Figure 12.
Our evaluation also makes a compelling case that
we need measurement information or external knowledge
on where links are most likely shared and where capacity estimates are
not accurate. Given such information, we can selectively avoid
overloading these links in the algorithms.
In this paper, we study the problem of placing cache servers in VPNs to provision for unicast based video streaming events. Our goal is to satisfy a given client population with the minimal number of cache servers. Given the bound on the number of cache servers, we add the additional goal of placing them in such a way as to minimize the total bandwidth usage. We developed provably optimal algorithms to achieve both goals using an interception cache server based solution. In addition, we prove that the problem is NP-hard in general. We then develop a set of simple and efficient heuristics to provide reasonable solutions to the cache placement problem if non-interception based redirection is used. Each of these solutions provide additional improvement in cache reduction at the expense of increased implementation cost compared to interception based redirection.
In addition to those theoretical results we performed extensive simulations to
evaluate the performance of our algorithms in realistic settings. We
discovered in particular that if non-interception based redirection systems
are used, the number of caches can be reduced by more than ![]() using our
heuristics compared to the greedy strategy for interception based
redirection. Additionally, in large networks, if redirection is based
on individual client IP addresses, our heuristics reduce the number of
caches by
using our
heuristics compared to the greedy strategy for interception based
redirection. Additionally, in large networks, if redirection is based
on individual client IP addresses, our heuristics reduce the number of
caches by ![]() compared to the case where redirection is based on
the router or the entire IP prefix ranges. If technologies such MPLS
is available to perform source routing, we show a flow-based algorithm
can improve up to
compared to the case where redirection is based on
the router or the entire IP prefix ranges. If technologies such MPLS
is available to perform source routing, we show a flow-based algorithm
can improve up to ![]() in the number of caches and is very close to
the actual optimal.
in the number of caches and is very close to
the actual optimal.
For future work, we intend to verify our algorithms by implementing it within a large VPN. We also plan to evaluate the robustness of flow-based algorithm in presence of inaccurate input data and more thoroughly study the benefit in bandwidth saving using our proposed dynamic programming algorithm.
This document was generated using the LaTeX2HTML translator Version 2002 (1.62)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -dir HTML -noaddress -antialias -antialias_text -split 0 -white -nocontents_in_navigation -noindex_in_navigation -noauto_navigation -nonavigation -notop_navigation -nobottom_navigation -math -math_parsing -html_version 3.2 bw.tex
The translation was initiated by on 2003-03-03