Internet is becoming an increasingly prosperous network for many types of commerce. In electronic marketplaces, group buyings are seen as an effective form of electronic commerce. When buyers cooperate with each other, a seller can discount the price of a good. In many existing group buying sites, some sellers deal in the same sort goods or their imitations. Buyers form coalitions for each item on sale. However, buyers cannot always purchase goods at a lower price, because buyers' sub-groups are distributed. Thus, buyers need to search hard to find the goods they can purchase. In this paper, we propose a group buying marketplace on the Internet. In our marketplace, buyers can purchase goods at a lower price by forming coalitions. In our system, buyers are integrated based on buyers' multi-attribute preferences (utilities). Our system supports buyers' decision making by using the Analytic Hierarchy Process. We propose some methods for group integration. Advantages of our market can be described as follows. (1) Buyers' multi-attribute utilities are reflected effectively in group integration. (2) Buyers can purchase goods at a lower price. (3) Buyers' payments are decided based on their degree of compromise. (4) A successful seller can sell goods in their stock.
Group buying, Group decision support system, E-market, AHP
As the Internet develops, it is becoming an increasingly prosperous network for many types of commerce. Group buying has become a particularly effective form of electronic commerce [1]. Group buying is a model in which multiple buyers cooperate and buy a good/service at a discount price. When buyers can cooperate with each other, a seller can discount the price of a good [3]. Multiple buyers can form coalitions with each other on the world wide web. In existing group buying sites, however, buyers cannot purchase goods at a lower price, because buyers' groups are often distributed on the web. Thus, each buyer in a group cannot purchase a good that satisfies his/her preference, therefore, each buyer's preference is not accurately reflected. To solve this problem, we propose a group integration support system for group buying. Buyers' groups are integrated into another buyers' group in our system. Our system can support group buying in which the users' preferences are reflected when effectively trading. In this work, we propose a group integration support system for group buying. Here, we assume the multi-attribute utility theory: when buyers purchase goods, buyers have multi-attribute preferences in goods selection. Our system supports the group integration based on multi-attribute utility theory. This example relates to buying a personal computer. Personal computers have the following attributes: memory, hard disk, price, and so on. It is important that multi-attribute preferences are satisfactory for all buyers.
The rest of the paper is organized as follows. In section 2, we propose a new group buying support system. In section 3, we show the advantages of our system. Finally in Section 4, we provide some final remarks.
We consider a situation in which
there are multiple goods and multiple buyers in
group buying sites.
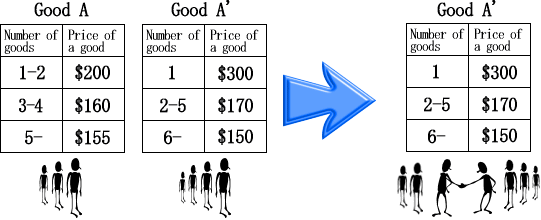
In Figure 1, the left figure shows buyer group distribution.
 |
| Figure 1. A buyers' groups distribution and a buyers integration |
We assume the multi-attribute utility theory.
A buyer's preference is shown as a utility function.
A utility function consists of multiple independent attributes based on
MAUT ( Multi Attribute Utility Theory ) [2]. In general,
MAUT handles problems for which outcomes are characterized by two or more
attributes. For example, purchasing a new car requires consideration of the
price, the shape, the color, the type, etc. In MAUT, for an alternative
Ci, the attributes X1, X2, ..., Xn exist, and their values are
x1(Ci), x2(Ci), ...,xn(Ci).
We can represent the utility u(Ci) for the attribute Ci as
In this section we show an algorithm of buyers or buyer group integration. Goods weights are calculated based on pairwise comparison matrices in the AHP. A group's pairwise comparison matrix is made by calculating the geometrical mean of the each element of the matrix, which the buyer decides. A group's weighting for goods is decided based on the group's pairwise comparison matrix.
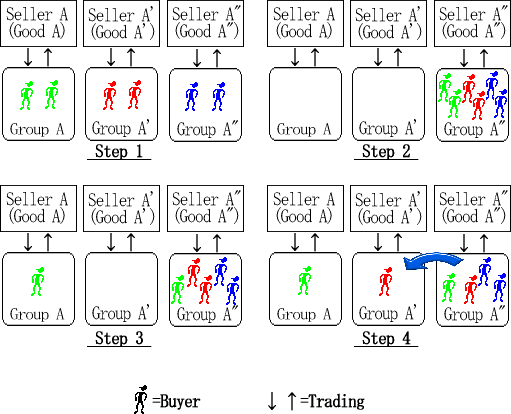 |
| Figure 2. A coordination of the integration |
In [Step 1], if each buyer can purchase good at the lowest price, the process finishes and each buyer purchases a good (step1 in Figure 2). If each buyer cannot purchase a good at the lowest price, the process progresses to [Step 2]. In [Step 2], if all buyers' utilities are reflected effectively by integration, the process finishes and the integrated buyers trade with a seller (step2 in Figure 2). Group integration is effective on price; however, there are cases where buyers' utilities are not reflected effectively. We propose a novel algorithm for group integration in a later description. In [Step 2], if the condition is not satisfied, the process proceeds to [Step 3]. In [Step 3], buyers satisfy conditions that are pre-integrated into a group (step3 in Figure 2). The data is reserved and used for comparison with [Step 4]'s data in [Step 5]. In [Step 4], utilities of buyers pre-integrated in [Step 3] are not reflected, so the buyers select again before pre-integration (step4 in Figure 2). The data is reserved and used for comparison with [Step 3]'s data in [Step 5]. In [Step 5], a comparison of [Step 3]'s data and [Step 4]'s data is conducted. The larger data is adopted for group integration. The group integration 1 and 2 in the Fig. 2 is selected, otherwise the buyers are not integrated and purchase the goods he/she selected before pre-integration.
We conducted an experiment to present the algorithm's effectiveness. We evaluated the following case concerned with buyer's utility and payment amount. The cases are individual purchase, simple group buying, and group integration. We assume three goods are registered, and ten buyers who evaluate substitutes are participate in the E-Group Buying Market. The reservation price of each buyer is decided based on uniform distribution between $1,000 and $2,000. The price of each good is decided based on information from a real group buying site. In this experiment, we assume there is no upper limit in the number of goods. Comparisons of buying methods are as follows. [Individual buying] is not group buying. [Simple group buying] is a buying method of existing group buying. [Group integration 1] is a buying method using our algorithm [Step 2]. [Group integration 2] is a buying method using our algorithm [Step 3] or [Step 4].
The experiments are investigated in the following Case 1 to
Case 3.
Case 1 In this case, each buyer's evaluated price
is not important in pairwise comparison.
Case 2 In this case, each buyer's evaluation of each attribute
is important, as in pairwise comparison.
Case 3 In this case, each buyer's evaluated price
is important in pairwise comparison.
Table 1 shows a comparison of buyers' utilities and sum total between [simple group buying] and [group integration]. The improvement ratio is calculated by dividing the utility in the [simple group buying] by the utility. The geometric mean of utilities in [group integration 2] is higher than in [simple group buying]. For [group integration 2], it calculated the discount rate by dividing the sum total in [simple group buying] by the sum total in [group integration 2]. Thus, discount rate in [group integration 2] is higher than in [simple group buying]. Therefore, our algorithm is reflected favorably in terms of buyers' utilities and payment amount by group integration.
| Buyers' utilities | Case 1 | Case 2 | Case 3 |
| Simple group buying | 0.50350 | 0.45172 | 0.53248 |
| Group integration 2 | 0.54184 | 0.54259 | 0.56485 |
| Rate of improvement | 8% | 20% | 6% |
| Sum total | Case 1 | Case 2 | Case 3 |
| Simple group buying | 0.50350 | 0.45172 | 0.53248 |
| Group integration 2 | 0.54184 | 0.54259 | 0.56485 |
| Rate of improvement | 8% | 20% | 6% |
In this paper, we proposed an E-Group Buying Market, which has a system for group buying dealing in substitute goods. The system can realize that buyers' utilities and payment amount are reflected effectively by group integration. In the system, buyers' utilities are shown based on a multi-attribute utility theory using the AHP. We proposed and indicated effectiveness of an algorithm for group integration. A buyer's payment amount is decided based on compromise value, and the system using fee is decided based on the value. In the experiment, [group integration 2] in our algorithm is superior to [simple group buying] with respect to buyers' utilities and sum totals. Advantages of our market are as follows. (1) It realizes trading that reflects buyers' multi-attribute preferences. (2) Each buyer can purchase a good at a lower price before group integration. (3) A buyer's payment amount is decided based on compromise value. (4) Successful sellers can trade with more buyers.