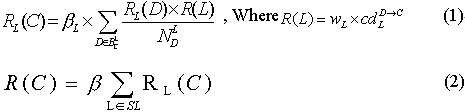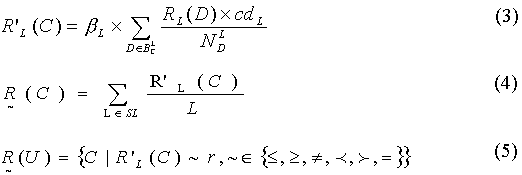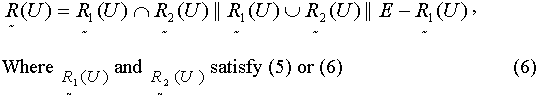Ranking Semantic-linked Network
Hai Zhuge
Knowledge Grid
Research Group, Key Laboratory of Intelligent Information Processing
Institute
of Computing Technology, Chinese Academy of Sciences, P.O.Box 2704, Beijing, 100080, China
zhuge@ict.ac.cn
Liping Zheng
Knowledge Grid
Research Group, Key Laboratory of Intelligent Information Processing
Institute
of Computing Technology, Chinese Academy of Sciences, P.O.Box 2704, Beijing, 100080, China
zhengliping@263.net
ABSTRACT
Traditional link analysis approaches used in web retrieval only apply to rank
hyperlinked web pages. This paper introduces the notion of semantic-linked
network consisting of semantic links and semantic components, and proposes an
approach for ranking the semantic-linked network, which effectively quantifies
the semantic importance of semantic components.
Keywords
Link analysis, ranking algorithm, semantic component, semantic link
1. INTRODUCTION
The current web is based on the HTTP and HTML. The Semantic Web extends the
current web by making the web resources machine-understandable [3]. Markup
languages like XML [1], OIL [2], DAML [4] have been suggested by the semantic
web community. Other efforts towards the next-generation web include the Grid (http://www.gridforum.org),
the emerging Semantic Grid [6] and Knowledge Grid (http://kg.ict.ac.cn).
Different from direct semantics expression of web resources, we suggest a
set of semantic links to describe the semantic relationship between relevant
resources: 1) Cause-effect link (C1¾ce→C2):
C1 is the cause of C2; 2) Implication link (C1¾imp→C2):
the semantics of C1 implies that of C2; 3) Subtype link
(C1¾st→C2):
C2 is a part of C1; 4) Similar-to link (C1¾(sim,
sd)→C2): the semantics of C2 is similar to
that of C1, and sd is the similarity degree; 5) Instance link
(C1¾ins→C2):
C2 is the instance of C1; 6) Sequential link (C1¾seq→C2):
the content of C2 is successor of that of C1; 7) Reference
link (C1¾ref→C2):
C2 is further explanation of C1; 8) Undefined link
(C1¾und→C2):
there is no obvious semantic relationship between C1 and C2
[7]. Semantic links can be inexact (C1¾(L,
cd) → C2): L is some semantic link; cd is
the certainty degree of semantic relationships between resources C1
and C2.
A semantic component is a network consisting of arcs of semantic links and
small granularity semantic components. Basic semantic component element could be
all kinds of e-files like text and images. Semantic-linked network consists of
semantic-linked semantic components. Software tool able to mark semantic links
in a plain text has been implemented. Users can use ordinary browsers to browse
the semantic-linked network.
How to differentiate the importance of the semantic components in the
semantic-linked network becomes an important issue when browsing and searching
the network. Traditional Web search engines employs hyperlink analysis approach
and ranking algorithms (such as the PageRank algorithm [5]) to enhance the
effectiveness of web page retrieval by sorting the retrieval results according
to rank order. This paper proposes an algorithm similar to PageRank to rank the
semantic components in the network.
2. Semantic Component Ranking Algorithm
Semantic link structure reflects the relevance among semantic components,
just as hyperlink structure reflects the relevance of current web pages.
Naturally we refer to link analysis to solve the ranking issue of the
semantic-linked network. But in PageRank, every web page has only one rank
dealing with hyperlinks. In the semantic-linked network we must consider
multiple semantics expressed by different types of semantic link. For a semantic
component, we compute eight individual L-ranks, dealing with different L-links
respectively. L-rank is computed by algorithm similar to PageRank: the L-rank
of a component is evenly distributed among all components it points to via L–link.
To give an overall rank, T-Rank is computed as follows: select link types
that need to compute L-rank, assign each chosen L-rank a weight wL
according to semantic priority rule: ref £
ins £
st £
imp £
ce, then sum up all chosen L-ranks proportionally according to wL.
Let C, D be components, SL = {ce, imp, st,
ref, ins, sim, seq, und},
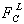 be the set of components C points to by L-link and
be the set of components C points to by L-link and
 be the set of components that point to C by L-link.
be the set of components that point to C by L-link.
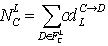 is the sum of certainty degree of all L-links from C. βL
(or β) is a factor for normalization. L-rank (RL(C))
and T-Rank (R(C)) of C are defined as formula (1)
and (2):
is the sum of certainty degree of all L-links from C. βL
(or β) is a factor for normalization. L-rank (RL(C))
and T-Rank (R(C)) of C are defined as formula (1)
and (2):
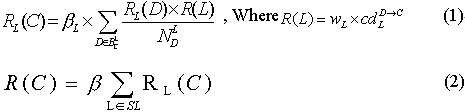
Experiments demonstrate that the proposed algorithm has the convergence
properties. Figure 1 shows the mean number of iterations of L-Rank and
that of PageRank based on link databases with the same link structure: As number
of links increases L-Rank algorithm converges faster whereas PageRank
algorithm converges slower though their convergence curves both tend to become
smooth; L-Rank algorithm converges slightly slower than PageRank
based on the same link structure. The main cause is semantic links refine the
hyperlinks by adding semantic certainty degree.
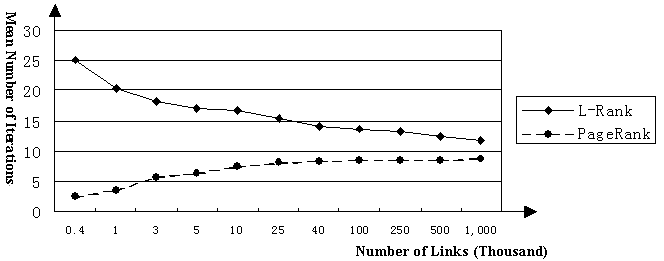
Figure
1. Convergence properties comparison between
L-Rank
and PageRank.
To improve the L-Rank algorithm and obtain better ranking results, we
employ any of the following four filtering methods to pre-treat semantic-linked
network: Method 1 groups components by topics or subjects and filters those
components not belonging to the specified category. Method 2 filters
irrelevant semantic links by matching anchor text of link with keywords of
query, thus semantic links irrelevant to keywords are abridged in a mass. Method
3 applies Method 1 first and then Method 2 next. Method 4 applies Method 2 first
and then Method 1 next.
3. PERSONALIZED RANKING
To meet
needs of users’ personal interests, we further propose a personalized ranking
algorithm where fuzzy-set rank (defined as formula (3) and (4))
is used to
record the contribution of different semantic links to the rank of a semantic
component. Formula
(5) and (6) defines the personalized rank.
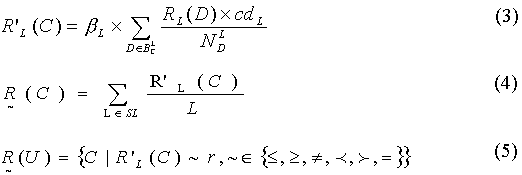
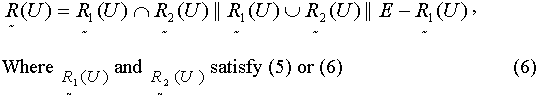
4. ANALYSIS AND COMPARISON
The relationship between the proposed ranking algorithms
and filtering methods is illustrated in Figure 2. L-Rank is the basic algorithm
to compute the individual rank based on L-link. T-Rank and Fuzzy-set Rank
are two
description forms of rank. By taking into account users’ personal view,
Personalized Rank is the refinement of Fuzzy-set Rank. Methods 1 – 4 are used
to reduce the number of semantic components and links for ranking.
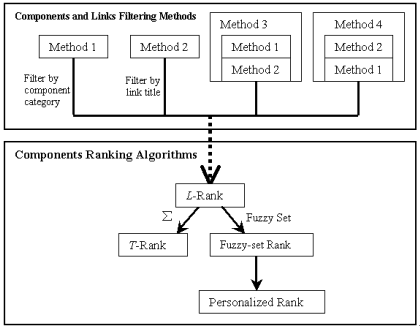
Figure
2. Relationship
between ranking algorithms
and filtering methods.
Traditional
link analysis approaches are based on the current web. The approach we propose
is based on the semantic-linked network, which establishes semantic
interconnection among resources. Semantic components and semantic links contain
richer semantics than the HTML web pages and the simplex hyperlinks.
The proposed filtering methods reduce the scale of semantic components and
semantic links that need to rank. By comparison, traditional link analysis
approaches do not support link filtering so as to obtain more effective
retrieval.
5. SUMMARY
This paper introduces the notion of semantic-linked
network to extend the current hyperlinked web. The network is composed of
semantic components and semantic links, and a semantic component can be also a
semantic-linked network. An effective approach for ranking the semantic-linked
network is proposed. The approach consists of the basic ranking algorithm,
the personalized ranking algorithm based on fuzzy-set rank representation, and
the methods for filtering semantic components and semantic links. Ongoing work
includes setting more rational evaluation criteria for components evaluation and
optimizing the ranking algorithms to get better performance.
6. ACKNOWLEDGEMENTS
This work was supported by the National Science Foundation of China (NSFC).
7. REFERENCES
- S.Decker et al. The Semantic Web: The Roles of XML and RDF, IEEE Internet
Computing, September/October 2000, 63-74.
- D.Fensel, et al. OIL: An Ontology Infrastructure for the Semantic Web,
IEEE Intelligent Systems, 16(2), March/April 2001, 38-45.
- J.Heflin and J.Hendler. A Portrait of the Semantic Web in Action, IEEE
Intelligent Systems, 16(2), March/April 2001, 54-59.
- J.Hendler and D.McGuinness. The DARPA Agent Markup Language, IEEE
Intelligent Systems, 15(6), November/December 2000, 72-73.
- L.Page, S.Brin, R.Motwani, and T.Winograd. The Pagerank Citation Ranking:
Bringing Order to the Web, Technical Report, Stanford, Santa Barbara, CA
93106, January 1998.
- H.Zhuge. A Knowledge Grid Model and Platform for Global Knowledge Sharing,
Expert Systems with Applications, 22(4), 2002, 313-320.
- H.Zhuge. Active Document Framework ADF: Concept and Method, in Proceedings of the 5th
Asia Pacific Web Conference, April 23-25, Xian, China, 2003.
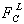 be the set of components C points to by L-link and
be the set of components C points to by L-link and
 be the set of components that point to C by L-link.
be the set of components that point to C by L-link.
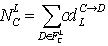 is the sum of certainty degree of all L-links from C. βL
(or β) is a factor for normalization. L-rank (RL(C))
and T-Rank (R(C)) of C are defined as formula (1)
and (2):
is the sum of certainty degree of all L-links from C. βL
(or β) is a factor for normalization. L-rank (RL(C))
and T-Rank (R(C)) of C are defined as formula (1)
and (2):