In this paper, we present a localized algorithm for constructing power-efficient topology for wireless ad hoc networks. The constructed topology is sparse, has a constant bounded power stretch factor, and the total transmission power is low. In addition, the time complexity of our algorithm to generate a solution is also low and the energy for each mobile node can thus be further saved, as computations also consume power from a mobile computer.
Wireless ad hoc networks, topology control, power consumption.
A wireless ad hoc network is formed from mobile nodes without using an infrastructure. The lack of a physical backbone poses a strong need of topology control of the network. Also, due to the finite power supply of a mobile computer, power conservation has been widely used as a primary control parameter in the design of protocols for ad hoc networks. Therefore, the problem of power-efficient topology control has been attracting more and more researchers from the areas of mobile computing and networking.
A wireless ad hoc network can be modeled by a weighted directed graph G = (V, E), where V represents the set of all the mobile nodes and E represents a set of edges. Edge (u, v) Î E if and only if node v is in the transmission range of node u. We use ||uv|| to denote the Euclidean distance between node u and node v. The weight of the edge (u, v) is the power consumed for transmitting signal from node u to node v. It's value can be formulated as ||uv|| b in the most widely-used power-attenuation model, where b is a real constant between 2 and 5 depending on the wireless transmission environment. This power consumption is typically called transmitter power and is treated as the major part of power consumption to transmit signals.
In this paper, we assume that each mobile node has a GPS receiver for acquiring its own location information. We assume that initially all mobile nodes are operated at full transmission power and have the transmission radius equal to one unit by a proper scaling. Consequently, the resulted graph G will be a unit-disk graph (denoted as UDG (V))and there is an edge between two nodes if and only if their Euclidean distance is at most one. We assume that UDG (V) is strongly connected and all mobile nodes have unique identifiers (ID). Wireless ad hoc networks are power constrained, and it is thus undesirable to ask each node to transmit with maximum power. As a result, each mobile node should adjust its transmission power to potentially reduce the total power consumption while still maintain network connectivity. Due to the characteristics of wireless ad hoc networks, it is preferred that the underlying network topology can be constructed in a localized manner. Let f be a complete transmission power assignment on V and Gf be the associated communication graph. We adopt the definitions of total-cost of f and power stretch factor of Gf given in [1].
In [3] Rodoplu and Meng described a distributed protocol for constructing a topology that guarantees the least-power path between every pair of nodes that are connected in a given graph. Recently, Li et al. [4] proposed a protocol based on their results but performs better and is computationally simpler. In [5] Li and Wan proposed a distributed position-based protocol to construct an enclosure graph for conserving power in one communication session. All these works focus on constructing a subgraph of G that contains the minimum-power topology, namely, a subgraph that is the union of all the least-power paths. On the other hand, the problems of finding a complete transmission power assignment with optimization criteria of the maximum or total transmission power assigned has been studied in [6,7]. In [1] Li et al. discussed the trade-off between sparseness and power efficiency of the topology. They also studied the power efficiency property of several well-known proximity graphs.
For simplicity, we first assume that each node in the network is stationary. While considering a complete transmission power assignment f, there is obviously a trade-off between total-cost of f and power stretch factor of Gf since reducing the transmission power of each node may diminish least-power paths or vice versa. The problem of finding a complete transmission power assignment f whose total-cost is the minimum among all complete assignments is called the min-total assignment problem. However, this problem is NP-hard and it is still an open question for the best approximation ratio. Therefore, our algorithm is designed in such a way that we first construct a subgraph of G that has a constant bounded power stretch factor. After that, the total transmission power consumption is minimized as much as possible. The basic idea is using the local information of each node to excise some logical links of the subgraph while still keeps the power stretch factor being bounded by a constant c.
Our algorithm consists of two phases. In the first phase we construct the constrained Gabriel graph GG (G) over the unit disk graph UDG (V). Here we choose GG (G) since it can be constructed locally and efficiently and has a power stretch factor one. In addition, the constrained Gabriel graph was used as a subgraph in several important routing protocols. Nevertheless, any other geometry structure that guarantees a constant bounded power stretch factor can be used in this phase. Suppose that GG (G) is associated with a transmission power assignment f. For each node u, if a logical link (u, v) of GG (G) satisfies the equation ||uv|| b = f (u), then (u, v) is called a critical link. The transmission radius associated with f (u) is denoted by radius (u). For each node u, the amount of transmission power saved by excising all its critical links is denoted by ps (u). The priority of node u is a pair pri (u) = <ps (u), ID>, where ID is used to break the ties. Each node is only required to know the locations, priorities and the transmission radiuses of the nodes within its two-hop neighborhood of UDG (V).
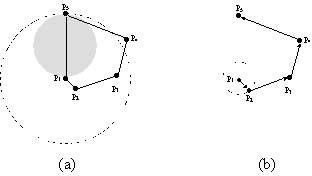
In the second phase, we eliminate the critical links that are replaceable with alternative paths. For each critical link ( u, v), node u tries to search a path that reaches node v based on its local information. We call such path the replacing path of (u, v). Whenever a node u finds itself having the highest priority and ps (u) > 0 within its two-hop neighborhood, it starts a search for the replacing paths. The searching process is based on Dijkstra's algorithm. However, for each node u, no global knowledge of the network topology is available, consequently, we ask u to construct a subgraph G' (u) = (V', E') on top of GG (G) based on the location and transmission radius information of the nodes in its vicinity. A node vi belongs to V' if vi is within u's two-hop neighborhood of UDG (V). An edge (vi , vj) belongs to E' if ||vivj|| £ radius (vi) and (vi, vj) belongs to the edges of GG (G). After the construction of G' (u), node u applies Dijkstra's algorithm on it to search for the shortest path Pmin (u, v). If no such path exists or p (Pmin (u, v )) is more than c times larger than the weight of (u, v), then the searching procedure is ended and ps (u) is set to 0. Otherwise, Pmin (u, v) is the eligible replacing path of (u, v), and (u, v) is excised. Figure 1. gives a illustration: in Figure 1 (a) the solid lines are the logical links of GG (G) and are all bi-directional. The area covered by the dotted line is the transmission range of p1. Note that there should be no other node in the gray area. The transmission range (and thus the transmission power) of p1can be largely reduced by applying our algorithm as shown in Figure 1(b).

Figure 1. Illustrative example.
If all the critical links are excised, the priority of u is recalculated, with the critical links decided by a new value of f (u) that corresponds to the minimum operational power needed to cover the remaining logical links. Node u then disseminates its new priority and replacing paths to its two-hop neighborhood by a notification message. Each constituent link in the replacing paths is tagged as a replacing link. For each node w with ps (w) > 0, if w receives a notification message, it first checks if any of its critical links is tagged as replacing, if yes, w sets ps (w) to 0 and disseminates its new priority to its two-hop neighborhood. Otherwise, if node w finds its priority is the local maximum within its two-hop neighborhood, it starts to search the replacing paths following the above steps. This searching procedure is repeated until every node vi in the network has ps (vi) = 0.
In this paper, we show how to construct a power-efficient topology for wireless ad hoc networks in a localized manner. The topology constructed by our algorithm has several desired features such as sparse and constant bounded power stretch factor. To develop a localized algorithm for constructing topologies in which the total transmission power assigned is within a constant factor of the optimal cost and that its power stretch factor is still bounded by a constant should be of interesting work.