Web Page Scoring Systems
for Horizontal and Vertical Search
Michelangelo Diligenti
Dipartimento di Ingegneria dell'Informazione
Via Roma 56 - Siena, Italy
diligmic@dii.unisi.it
Marco Gori
Dipartimento di Ingegneria dell'Informazione
Via Roma 56 - Siena, Italy
marco@dii.unisi.it
Marco Maggini
Dipartimento di Ingegneria dell'Informazione
Via Roma 56 - Siena, Italy
maggini@dii.unisi.it
Copyright is held by the author/owner(s).
WWW2002, May 7-11, 2002, Honolulu, Hawaii, USA.
ACM 1-58113-449-5/02/0005.
Abstract
Page ranking is a fundamental step towards the construction of effective
search engines for both generic (
horizontal) and
focused (
vertical) search.
Ranking schemes for horizontal search like the PageRank algorithm used
by Google operate on
the topology of the graph, regardless of the page content. On the other
hand, the recent development of vertical portals (
vortals)
makes it useful to adopt scoring systems focussed on the topic and
taking the page content into account.
In this paper, we propose a general framework for Web Page Scoring
Systems (WPSS) which incorporates and extends many of the relevant
models proposed in the literature. Finally, experimental results are given
to assess the features of the proposed scoring
systems with special emphasis on vertical search.
Categories and Subject Descriptors
F.2.2 [Analysis of Algorithms and Problem Complexity]: Nonnumerical
Algorithms and Problems - Sorting and Searching;
H.3.3 [Information Storage and Retrieval]: Information Search and
Retrieval - Information Filtering;
H.5.4 [Information Interfaces and Presentation]: Hypertext/Hypermedia
General terms
Algorithms
Keywords
Web Page Scoring Systems, Random Walks,
HITS, PageRank, Focused PageRank
The analysis of the hyperlinks on the Web [1]
can significantly increase the capability of search engines.
A simple counting of the number of references does not take into account the
fact that not all the citations have the same authority.
PageRank[2]
is a noticeable example of a topological-based ranking criterion.
An interesting example of query-dependent criteria is
given in [3].
User queries are issued to a search engine in order to create a set of
seed pages. Crawling the Web forward and backward from that seed
is performed to mirror the Web portion containing the information which
is likely to be useful. A ranking criterion based on topological
analyses can be applied to the pages belonging to the selected Web portion.
Very interesting results in this direction have
been proposed in [4,5,6].
In [7] a Bayesian approach is used to
compute hub and authorities, whereas in [8] both
topological information and information about page content are included
in distillation of information sources performed by a Bayesian approach.
Generally speaking, the ranking of hypertextual documents is expected
to take into account the reputation of the source,
the page updating frequency, the popularity,
the speed access, the degree of authority, and the
degree of hubness.
The page rank of hyper-textual documents can be thought of as a function of
the document content and the hyperlinks.
In this paper, we propose a general framework for Web Page Scoring Systems
(WPSS) which incorporates and extends many of the relevant models
proposed in the literature. The general web page scoring model proposed in
this paper extends both PageRank [2]
and the HITS scheme
[3].
In addition, the proposed model exhibits a number of novel features, which turn
out to be very useful especially for focused (vertical) search.
The content of the pages is combined with the web graphical structure
giving rise to scoring mechanisms which which are focused on a specific
topic. Moreover, in the proposed model, vertical search schemes can
take into account the mutual relationship amongst different topics.
In so doing, the discovery of pages with high score for a given topic
affects the score of pages with related topics.
Experimental results were carried out to assess the features of the
proposed scoring systems with special emphasis on vertical search. The
very promising experimental results reported in the paper provide a clear
validation of the proposed general scheme for web page scoring systems.
Page Rank and Random Walks
Random walk theory has been widely used to compute the absolute relevance
of a page in the Web [2,6].
The Web is represented as a graph
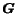 , where each Web page
is a node and a link between two nodes represents a hyperlink
between the associated pages.
A common assumption is that the relevance
, where each Web page
is a node and a link between two nodes represents a hyperlink
between the associated pages.
A common assumption is that the relevance 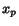 of page
of page 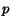 is represented by the probability of ending up in that page during
a walk on this graph.
is represented by the probability of ending up in that page during
a walk on this graph.
In the general framework we propose, we consider a complete model of
the behavior of a user surfing the Web. We assume that a Web surfer can
perform one out of four atomic actions at each step of his/her traversal of the
Web graph:
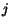 jump to a node of the graph;
jump to a node of the graph;
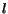 follow a hyperlink from the current page;
follow a hyperlink from the current page;
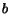 follow a back-link (a hyperlink in the inverse direction);
follow a back-link (a hyperlink in the inverse direction);
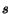 stay in the same node.
stay in the same node.
Thus the set of the atomic actions used to move on the Web is
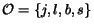 .
.
We assume that the behavior of the surfer depends on the page he is
currently visiting. The action he/she will decide to take will depend
on the page contents and the links it contains. For example if the
current page is interesting to the surfer, it is likely he/she
will follow a hyperlink contained in the page. Whereas, if the page is not interesting,
the surfer will likely jump to a different page not linked by the current one.
We can model the user behavior by a set of probabilities which depend
on the current page:
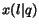 the probability of following one hyperlink from page
the probability of following one hyperlink from page  ,
,
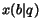 the probability of following one back-link from page
the probability of following one back-link from page  ,
,
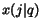 the probability of jumping from page
the probability of jumping from page  ,
,
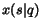 the probability of remaining in page
the probability of remaining in page  .
.
These values must satisfy the normalization constraint
Most of these actions need to specify their targets. Assuming that the
surfer's behavior is time-invariant, then we can model the targets
for jumps, hyperlink or back-link choices by using the following parameters:
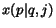 the probability of jumping from page
the probability of jumping from page  to page
to page 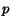 ;
;
 the probability of selecting a hyperlink from page
the probability of selecting a hyperlink from page  to page
to page  ;
this value is not null only for the pages
;
this value is not null only for the pages 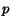 linked directly by page
linked directly by page  ,
i.e.
,
i.e. 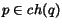 , being
, being 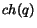 the set of the children of node
the set of the children of node  in the graph
in the graph
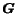 ;
;
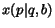 the probability of going back from page
the probability of going back from page  to page
to page 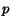 ;
this value is not null only for the pages
;
this value is not null only for the pages 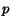 which link directly page
which link directly page  ,
i.e.
,
i.e. 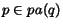 , being
, being 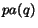 the set of the parents of node
the set of the parents of node  in the graph
in the graph
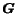 .
.
These sets of values must satisfy the following probability normalization constraints
for each page
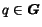 :
:
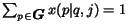 ,
,
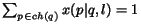 ,
,
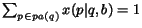 .
.
The model considers a temporal sequence of actions performed by the surfer
and it can be used to compute the probability that the surfer
is located in page 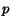 at time
at time 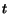 ,
, 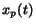 . The probability
distribution on the pages of the Web is updated by taking into
account the possible actions at time
. The probability
distribution on the pages of the Web is updated by taking into
account the possible actions at time 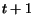 using the following
equation
using the following
equation
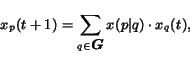 |
(1) |
where the probability 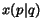 of going from page
of going from page  to page
to page 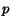 is
obtained by considering the action which can be performed by the
surfer. Thus, using the previous definitions for the actions,
the equation can be rewritten as
is
obtained by considering the action which can be performed by the
surfer. Thus, using the previous definitions for the actions,
the equation can be rewritten as
These probabilities can be collected in a 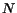 -dimensional vector
-dimensional vector
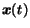 , being
, being 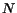 the number of pages in the Web graph
the number of pages in the Web graph
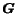 ,
and the probability update equations can be rewritten in a matrix form.
The probabilities of moving from a page
,
and the probability update equations can be rewritten in a matrix form.
The probabilities of moving from a page  to a page
to a page 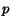 given
an action can be organized into the following matrices:
given
an action can be organized into the following matrices:
- the forward matrix
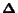 whose element
whose element  is the
probability
is the
probability 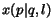 ;
;
- the backward matrix
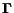 collecting the probabilities
collecting the probabilities
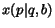 ;
;
- the jump matrix
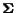 which is defined by
the jump probabilities
which is defined by
the jump probabilities 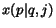 .
.
The forward and backward matrices are related to the Web adjacency matrix
 whose entries are 1 if page
whose entries are 1 if page 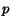 links page
links page  . In particular,
the forward matrix
. In particular,
the forward matrix
 has non null entries only in the
positions corresponding to 1s in matrix
has non null entries only in the
positions corresponding to 1s in matrix
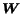 , and the backward matrix
, and the backward matrix
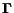 has non null entries in the positions corresponding
to 1s in
has non null entries in the positions corresponding
to 1s in
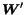 .
.
Further, we can define the set of action matrices which collect
the probabilities of taking one of the possible actions from a given page  .
These are
.
These are 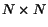 diagonal matrices defined as follows:
diagonal matrices defined as follows:
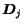 whose diagonal values
whose diagonal values 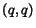 are the probabilities
are the probabilities 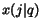 ,
,
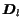 collecting
the probabilities
collecting
the probabilities 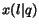 ,
,
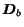 containing the values
containing the values 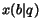 , and
, and
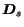 having on the diagonal the probabilities
having on the diagonal the probabilities 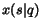 .
.
Hence, equation (2) can be written in
matrix form as
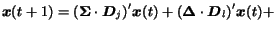 |
|
|
(3) |
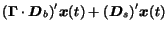 |
|
|
|
The transition matrix
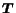 used to update the probability distribution is
used to update the probability distribution is
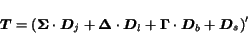 |
(4) |
Using this definition, the equation
(3) can be written as
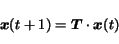 |
(5) |
Starting from a given initial distribution
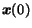 equation
(5) can be applied
recursively to compute the probability distribution at a given
time step
equation
(5) can be applied
recursively to compute the probability distribution at a given
time step 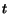 yielding
yielding
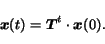 |
(6) |
In order to define an absolute page rank for the pages on the Web,
we consider the stationary distribution of the Markov chain
defined by the previous equations.
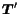 is the state transition matrix of
the Markov chain.
is the state transition matrix of
the Markov chain.
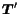 is stable, since
is stable, since
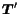 is a stochastic matrix having its maximum eigenvalue equal to
is a stochastic matrix having its maximum eigenvalue equal to 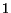 .
Since the state vector
.
Since the state vector
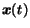 evolves following the equation
of a Markov Chain, it is guaranteed that if
evolves following the equation
of a Markov Chain, it is guaranteed that if
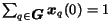 , then
, then
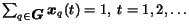 .
.
By applying the results on Markov chains (see e.g. [9]),
we can prove the following proposition.
Proposition 2.1
If
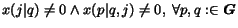
then
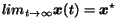
where
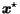
does not depend on the initial state vector
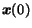
.

In order to simplify the general model proposed so far, we
can introduce some assumptions on the probability matrices.
A possible choice is to consider some actions to be
independent on the current page. A first hypothesis we
investigate is the case of jump probabilities which
are independent on the starting page  . This choice models
a surfer who decides to make random jumps from a given page
to another page with uniform probability. Thus, the jump
matrix
. This choice models
a surfer who decides to make random jumps from a given page
to another page with uniform probability. Thus, the jump
matrix
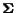 has all the entries equal to
has all the entries equal to
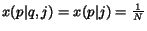
Moreover, we suppose that also the probability of choosing a
jump among the available actions does not depend on the page,
i.e.
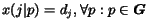 . Under these two assumptions,
equation (3) becomes
. Under these two assumptions,
equation (3) becomes
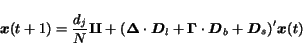 |
(7) |
because
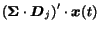 =
=
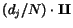 as
as
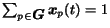 .
.
If we define
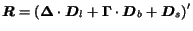 ,
the solution of equation (7) is
,
the solution of equation (7) is
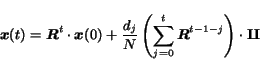 |
(8) |
Using the Frobenius theorem on matrices, the following bound on the maximum
eigenvalue of
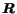 can be derived
can be derived
because
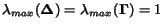 .
Hence, in equation
(8)
the first term vanishes as
.
Hence, in equation
(8)
the first term vanishes as
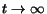 , i.e.
, i.e.
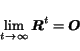 |
(10) |
where
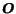 is the matrix having all elements equal to
is the matrix having all elements equal to 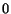 .
Thus, when
.
Thus, when 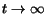 , the probability distribution
, the probability distribution
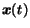 converges to
converges to
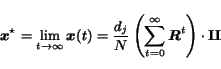 |
(11) |
Since
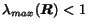 as shown in equation (9),
it can be proven that the previous equation converges to
as shown in equation (9),
it can be proven that the previous equation converges to
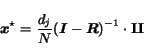 |
(12) |
As it is stated by proposition 2.1,
the value of
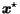 does not depend on the choice of the initial state vector
does not depend on the choice of the initial state vector
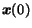 .
.
Multiple State Model
A model based on a single variable may not capture the complex relationships among
Web pages when trying to model their importance. Ranking schemes based
on multiple variables have been proposed in
[3,6],
where a pair of variables are used to represents the concepts of
hubness and authority of a page.
In the probabilistic framework described so far, we can define a multivariable
scheme by considering a pool of Web surfers each described by a single variable.
Each surfer is characterized by his/her own way of browsing
the Web modeled by using different parameter values in each
state transition equation.
By choosing proper values for these parameters we can choose different
policies in evaluating the absolute importance of the pages. Moreover,
the surfers may interact by accepting suggestions from
each other.
In order to model the activity of 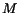 different surfers,
we use a set of state variables
different surfers,
we use a set of state variables
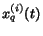 which represent
the probability of each surfer
which represent
the probability of each surfer 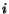 to be visiting page
to be visiting page  at time
at time
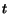 . The interaction among the surfers is modeled by a set of
parameters which define the probability of the surfer
. The interaction among the surfers is modeled by a set of
parameters which define the probability of the surfer 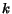 to accept
the suggestion of the surfer
to accept
the suggestion of the surfer 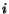 , thus jumping from the page he/she
is visiting to the one visited by the surfer
, thus jumping from the page he/she
is visiting to the one visited by the surfer 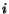 . This
interaction happens before the choice of the actions described previously.
If we hypothesize that the interaction does not depend on the
page the surfer
. This
interaction happens before the choice of the actions described previously.
If we hypothesize that the interaction does not depend on the
page the surfer 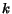 is currently visiting, the degree of
interaction with the surfer
is currently visiting, the degree of
interaction with the surfer 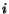 is modeled by the value
is modeled by the value
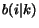 which represents the probability for the surfer
which represents the probability for the surfer 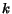 of jumping to
the page visited by the surfer
of jumping to
the page visited by the surfer 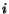 . These values must satisfy the
probability normalization constraint
. These values must satisfy the
probability normalization constraint
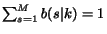 .
.
As an example, suppose that there are two surfers, ``the novice''
and ``the expert''. Surfer 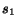 , the novice,
blindly trusts the suggestions of surfer
, the novice,
blindly trusts the suggestions of surfer 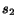 as he/she believes
as he/she believes
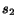 is an expert in discovering authoritative pages,
whereas
is an expert in discovering authoritative pages,
whereas 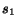 does not trust at all his/her own capabilities.
In this case the complete dependence of the novice on the expert
is modeled by choosing
does not trust at all his/her own capabilities.
In this case the complete dependence of the novice on the expert
is modeled by choosing 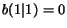 and
and 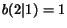 , i.e. the novice
chooses the page visited by the expert with probability equal to 1.
, i.e. the novice
chooses the page visited by the expert with probability equal to 1.
Before taking any action, the surfer 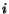 repositions himself/herself
in page
repositions himself/herself
in page 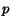 with probability
with probability
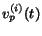 looking at the
suggestions of the other surfers. This probability is computed
as
looking at the
suggestions of the other surfers. This probability is computed
as
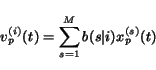 |
(13) |
Thus, when computing the new probability distribution
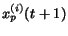 due to the action taken at time
due to the action taken at time 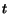 by the surfer
by the surfer 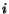 , we consider
the distribution
, we consider
the distribution
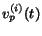 instead of
instead of
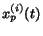 when
applying equation (2). Thus, the transition
function is defined as follows
when
applying equation (2). Thus, the transition
function is defined as follows
| |
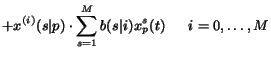 |
|
(14) |
When considering 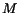 surfers, the score vectors of each surfer
surfers, the score vectors of each surfer
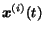 can be collected as the columns of a matrix
can be collected as the columns of a matrix
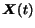 .
Moreover, we define the
.
Moreover, we define the ![$[M \times M]$](../../CDROM/refereed/629/img114.gif) matrix
matrix
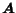 which
collects the values
which
collects the values 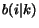 . The matrix
. The matrix
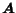 will be referred to
as the interaction matrix. Finally, each surfer
will be referred to
as the interaction matrix. Finally, each surfer 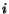 will be described by his/her own forward, backward and jump
matrices
will be described by his/her own forward, backward and jump
matrices
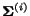 ,
,
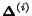 ,
,
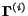 and by the action matrices
and by the action matrices
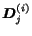 ,
,
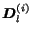 ,
,
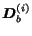 ,
,
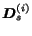 . Thus, the transition matrix for the Markov chain associated
to the surfer
. Thus, the transition matrix for the Markov chain associated
to the surfer 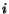 is
is
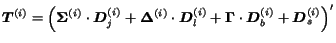 .
.
Using these definitions, the set of  interacting surfers can be described
by rewriting equation (14)
as a set of matrix equations as follows
interacting surfers can be described
by rewriting equation (14)
as a set of matrix equations as follows
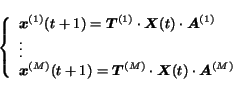 |
(15) |
When the surfers are independent on each other (i.e.
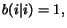
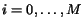 , and
, and
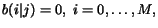
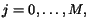
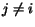 ),
the model reduces to
),
the model reduces to 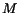 models as described by
equation (6).
models as described by
equation (6).
Horizontal WPSS
Horizontal WPSSs do not consider any information on the page contents
and produce the rank vector using just the topological characteristics
of the Web graph. In this section we show how these scoring
systems can be described in the proposed probabilistic framework.
In particular we derive the two most popular Page Scoring Systems,
PageRank and HITS, as special cases.
PageRank
The Google search engine employs a ranking scheme based on a
random walk model defined by a single state variable.
Only two actions are considered:
the surfer jumps to a new random page with probability 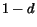 or he/she follows one link from the current page with probability
or he/she follows one link from the current page with probability 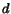 .
The Google ranking scheme, called PageRank, can be
described in the general probabilistic
framework of equation (2),
by choosing its parameters as follows. First, the probabilities
of following a back-link
.
The Google ranking scheme, called PageRank, can be
described in the general probabilistic
framework of equation (2),
by choosing its parameters as follows. First, the probabilities
of following a back-link 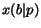 and of remaining in any page
and of remaining in any page
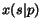 are null for all the pages
are null for all the pages 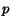 . Then, as stated above,
the probability of performing a random jump is
. Then, as stated above,
the probability of performing a random jump is
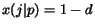 for any page
for any page 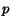 , whereas the probability of
following a hyperlink contained in the page
, whereas the probability of
following a hyperlink contained in the page 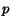 is
also a constant, i.e.
is
also a constant, i.e. 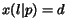 . Given that a jump is taken,
its target is selected using a uniform probability distribution
over all the
. Given that a jump is taken,
its target is selected using a uniform probability distribution
over all the 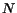 Web pages, i.e.
Web pages, i.e.
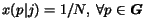 .
Finally, the probability of following the hyperlink from
.
Finally, the probability of following the hyperlink from  to
to 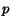 does not depend on the page
does not depend on the page 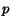 , i.e.
, i.e.
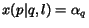 .
In order to meet the normalization constraint,
.
In order to meet the normalization constraint,
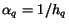 where
where 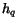 is the number of links exiting from page
is the number of links exiting from page  (the page
hubness). This assumption makes the surfer random, since
we define a uniform probability distribution among all
the outgoing links.
(the page
hubness). This assumption makes the surfer random, since
we define a uniform probability distribution among all
the outgoing links.
This last hypothesis cannot be met by pages which do not contain any
links to other pages. A page with no out-links is called sink page,
since it would behave just like a score sink in the PageRank propagation
scheme. In order to keep the probabilistic interpretation of
PageRank, all sink nodes must be removed.
The page rank of sinks is then computed from the page ranks of
their parents.
Under all these assumptions equation (2)
can be rewritten as
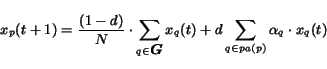 |
(16) |
Since the probabilistic interpretation is valid, it holds that
and, then, equation (16) becomes
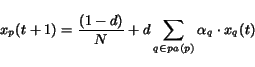 |
(17) |
Since 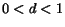 ,
,
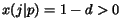 for each page and then
equation (12)
guarantees that the Google's PageRank converges to a distribution
of page scores that does not depend on the initial distribution.
for each page and then
equation (12)
guarantees that the Google's PageRank converges to a distribution
of page scores that does not depend on the initial distribution.
In order to apply the Google's PageRank scheme without removing
the sink nodes, we can introduce the following modification
to the original equations. Since no links can be followed from
a sink node  ,
, 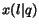 must be equal to
must be equal to 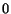 and
and 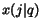 equal to
equal to 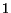 . Thus, when there are sinks,
. Thus, when there are sinks,
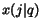 is defined as
is defined as
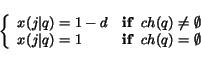 |
(18) |
In this case the contribution of the jump probabilities does not
sum to a constant term as it happens in equation (17),
but the value
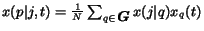 must be computed at the beginning of each iteration. This is the
computational scheme we used in our experiments.
must be computed at the beginning of each iteration. This is the
computational scheme we used in our experiments.
The HITS Ranking System
The HITS algorithm was proposed to model authoritative documents
only relying on the information hidden in the connections among
them due to co-citation or web hyperlinks
[3].
In this formulation the Web pages are divided into two page classes:
pages which are information sources (authorities) and
pages which link to information sources (hubs).
The HITS algorithm assigns two numbers to each page 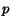 ,
the page authority and the page hubness
in order to model the importance of the page.
These values are computed by applying iteratively the
following equations
,
the page authority and the page hubness
in order to model the importance of the page.
These values are computed by applying iteratively the
following equations
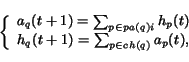 |
(19) |
where 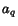 indicates the authority of page
indicates the authority of page  and
and 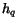 its hubness.
If
its hubness.
If
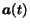 is the vector of
the authorities at step
is the vector of
the authorities at step 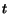 , and
, and
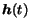 is the hubness vector at step
is the hubness vector at step 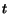 , the previous equation can be rewritten
in matrix form as
, the previous equation can be rewritten
in matrix form as
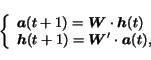 |
(20) |
where
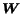 is the adjacency matrix of the Web graph.
It is trivial to demonstrate that as
is the adjacency matrix of the Web graph.
It is trivial to demonstrate that as 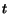 tends to infinity,
the direction of authority vector tends to be parallel
to the main eigenvector of the
tends to infinity,
the direction of authority vector tends to be parallel
to the main eigenvector of the
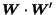 matrix,
whereas the hubness vector tends to be parallel to the main
eigenvector of the
matrix,
whereas the hubness vector tends to be parallel to the main
eigenvector of the
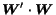 matrix.
matrix.
The HITS ranking scheme can be represented
in the general Web surfer framework, even if some of the assumptions will
violate the probabilistic interpretation.
Since HITS uses two state variables, the hubness and the authority of a page,
the corresponding random walk model is a multiple state scheme
based on the activity of two surfers. Surfer 1 is associated to the
hubness of pages whereas surfer 2 is associated to the authority
of pages. For both surfers the probabilities of remaining in the
same page 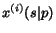 and of jumping to a random page
and of jumping to a random page
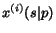 are null. Surfer 1 never follows a link, i.e.
are null. Surfer 1 never follows a link, i.e.
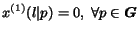 whereas he/she always follows
a back-link, i.e.
whereas he/she always follows
a back-link, i.e.
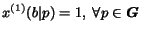 . Because of this, the
HITS computation violates the probability normalization constraints,
since
. Because of this, the
HITS computation violates the probability normalization constraints,
since
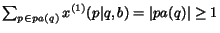 .
.
Surfer 2 has the opposite behavior with respect to surfer 1.
He/she always follows a link, i.e.
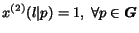 ,
and he/she never follows a back-link, i.e.
,
and he/she never follows a back-link, i.e.
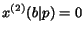 .
In this case the normalization constraint is violated for
the values of
.
In this case the normalization constraint is violated for
the values of 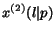 because
because
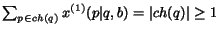 .
.
Under these assumptions
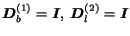 , being
, being
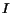 the identity matrix, whereas
the identity matrix, whereas
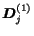 ,
,
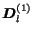 ,
,
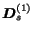 ,
,
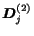 ,
,
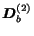 ,
,
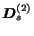 are
all equal to the null matrix.
are
all equal to the null matrix.
The interaction between the surfers is described by the matrix:
![\begin{displaymath}
\mbox{\boldmath$A$}= \left[
\begin{array}{cc}
0 & 1 \\
1 & 0 \\
\end{array} \right]
\end{displaymath}](../../CDROM/refereed/629/img170.gif) |
(21) |
The interpretation of the interactions represented by this matrix is
that surfer 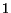 considers surfer
considers surfer 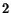 as an expert in
discovering authorities and always moves to the position suggested by
that surfer before acting. On the other hand, surfer
as an expert in
discovering authorities and always moves to the position suggested by
that surfer before acting. On the other hand, surfer 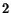 considers
surfer
considers
surfer 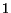 as an expert in finding hubs and then he/she always moves to
the position suggested by that surfer before choosing the next action.
as an expert in finding hubs and then he/she always moves to
the position suggested by that surfer before choosing the next action.
In this case equation
(15)
is
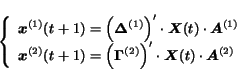 |
(22) |
Using equation (21) and
the HITS assumption
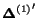

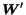 ,
,
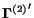

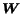 we obtain
we obtain
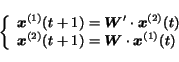 |
(23) |
which, redefining
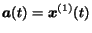 and
and
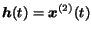 ,
is equivalent to the HITS computation of
equation (20).
,
is equivalent to the HITS computation of
equation (20).
The HITS model violates the probabilistic interpretation and this makes the
computation unstable, since the
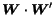 matrix has a principal
eigenvalue much larger then
matrix has a principal
eigenvalue much larger then 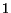 . Hence, unlike Google's PageRank, the HITS
algorithm needs the score to be normalized at the end of each iteration.
. Hence, unlike Google's PageRank, the HITS
algorithm needs the score to be normalized at the end of each iteration.
Finally, the HITS scheme suffers from other drawbacks. In particular,
large highly connected communities of Web pages tend to attract
the principal eigenvector of
 , thus pushing
to zero the relevance of all other pages. As a result the page
scores tend to decrease rapidly to zero for pages outside those
communities. Recently some heuristics have been proposed to avoid this
problem even if such behavior can not be generally avoided because
of the properties of the dynamic system associated to the HITS algorithm
[10].
, thus pushing
to zero the relevance of all other pages. As a result the page
scores tend to decrease rapidly to zero for pages outside those
communities. Recently some heuristics have been proposed to avoid this
problem even if such behavior can not be generally avoided because
of the properties of the dynamic system associated to the HITS algorithm
[10].
The PageRank-HITS model
PageRank is stable, it has a well defined behavior because of its
probabilistic interpretation and it can be applied to large page collections
without canceling the influence of the smallest Web communities.
On the other hand, PageRank is sometimes too simple to take
into account the complex relationships of Web page citations.
HITS is not stable, only the largest Web community influences the ranking,
and this does not allow the application of HITS to large page collections.
On the other hand the hub and authority model can capture more than
PageRank the relationships among Web pages.
In this section we show that the proposed probabilistic framework
allows to include the advantages of both approaches.
We employ two surfers, each one implementing a bidirectional PageRank surfer.
We assume that surfer  either follows a back-link with probability
either follows a back-link with probability
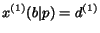 or jumps to a random page
with probability
or jumps to a random page
with probability
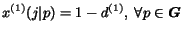 .
Whereas surfer
.
Whereas surfer 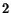 either follows a forward link with probability
either follows a forward link with probability
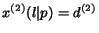 or jumps to a random page with probability
or jumps to a random page with probability
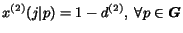 .
.
Like in HITS, the interaction between the surfers is described by the matrix
In this case, equation
(15)
becomes
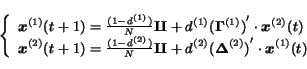 |
(24) |
Further, we assume the independence of parameters
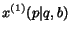 and
and
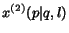 on the page
on the page 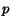 . Hence, it holds that
. Hence, it holds that
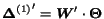 ,
,
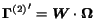 ,
where
,
where
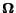 is the diagonal matrix with element
is the diagonal matrix with element 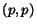 equal to
equal to 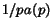 and
and
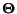 is the diagonal matrix with element
is the diagonal matrix with element 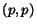 equal to
equal to 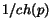 . Then:
. Then:
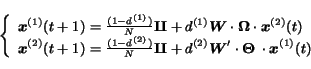 |
(25) |
This page rank is stable, the scores sum up to 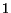 and no normalization
is required at the end of each iteration. Moreover, the two state variables
can capture and process more complex relationships among pages.
and no normalization
is required at the end of each iteration. Moreover, the two state variables
can capture and process more complex relationships among pages.
In particular, setting
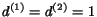 yields a normalized version
of HITS, which has been proposed in [4].
yields a normalized version
of HITS, which has been proposed in [4].
Vertical WPSS
Horizontal WPSSs exploit the information provided by the Web graph
topology. Different properties of the graph are evidenced by each
model. For example the intuitive idea that a highly linked page
is an absolute authority can be captured by PageRank or
HITS schemes. However, when applying scoring techniques for
focused search the page contents should be taken into account beside
the graph topology. Vertical WPSSs aim at computing a relative
ranking of pages when focusing on a specific topic. A vertical
WPSS relies on the representation of the page content with
a set of features (e.g. a set of keywords) and on a classifier
which is used to assess the degree of relevance of the page with
respect to the topic of interest. Basically the general probabilistic
framework of WPSSs proposed in this paper can be used to define
a vertical approach to page scoring. Several models can be derived
which combine the ideas underlining the topology-based scoring
and the topic relevance measure provided by text classifiers.
In particular a text classifier can be used to compute proper
values for the probabilities needed by the random walk model.
As it is shown by the experimental results, vertical WPSSs
can produce more accurate results in ranking topic specific pages.
Focused PageRank
In the PageRank framework, when choosing to follow
a link in a page  each link has the same probability
each link has the same probability 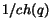 to be followed. Instead of the random surfer model,
in the focused domain we can consider the more realistic case
of a surfer who follows the links according to the
suggestions provided by a page classifier.
to be followed. Instead of the random surfer model,
in the focused domain we can consider the more realistic case
of a surfer who follows the links according to the
suggestions provided by a page classifier.
If the surfer is located at page  and the pages linked by page
and the pages linked by page  have scores
have scores
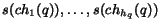 by a topic
classifier, the probability of the surfer to follow the
by a topic
classifier, the probability of the surfer to follow the 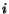 -th link
is defined as
-th link
is defined as
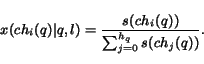 |
(26) |
Thus the forward matrix
 will depend on the classifier
outputs on the target pages.
will depend on the classifier
outputs on the target pages.
Hence, the modified equation to compute the combined page
scores using a PageRank-like scheme is
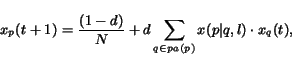 |
(27) |
where 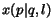 is computed as in equation (26).
is computed as in equation (26).
This scoring system removes the assumption of complete randomness of the
underlying Web surfer. In this case, the surfer is aware of what he/she is
searching, and he/she will trust the classifier suggestions following the links
with a probability proportional to the score of the page the links leads to.
This allows us to derive a topic-specific page rank.
For example: the ``Microsoft'' home is highly authoritative
according to the topic-generic PageRank, whereas it is not highly
authoritative when searching for ``Perl'' language tutorials, since
even if that page gets many citations, most of these citations will be scarcely
related to the target topic and then not significantly considered in the
computation.
Double Focused PageRank
The focused PageRank model described previously uses a topic specific
distribution for selecting the link to follow but the decision on the
action to take does not depend on the contents of the current page.
A more realistic model should take into account the fact that the
decision about the action is usually dependent on the contents of
the current page. For example, let us suppose that two surfers are searching
for a ``Perl Language tutorial'', and that the first one is located at the page
``http://www.perl.com'', while the second is located at the page
``http://www.cnn.com''. Clearly it is more likely that the first
surfer will decide to follow a link from the current page while
the second one will prefer to jump to another page
which is related to the topic he is interested in.
We can model this behavior by adapting the action probabilities
using the contents of the current page, thus modeling
a focused choice of the surfer's actions.
In particular, the probability of following a hyperlink
can be chosen to be proportional to the degree of relevance 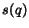 of the current
page with respect to the target, i.e.
of the current
page with respect to the target, i.e.
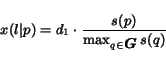 |
(28) |
where 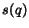 is computed by a text classifier.
is computed by a text classifier.
On the other hand, the probability of jumping away from a page decreases
proportionally to 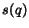 , i.e.
, i.e.
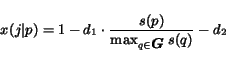 |
(29) |
Finally, we assume that the probability of landing into page after
a jump is proportional to its relevance 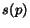 , i.e.
, i.e.
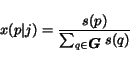 |
(30) |
Such modifications can be integrated into the focused PageRank
proposed in section 4.1 to model a focused
navigation more accurately. Equation
(12)
guarantees that the resulting scoring system
is stable and that it converges to a score distribution independent
from the initial distribution.
Experimental Results
Figure 1:
(a) The distribution of page scores for the topic ``Linux''.
(b) The distribution of scores for the topic ``cooking recipes''.
In both cases PageRank is much smoother that the
HITS one. The focused versions of the PageRank are still
smooth but concentrate the scores on a smaller set of authoritative
pages which are more specific for the considered topic.
![\includegraphics[width=60mm]{linuxDistribution.eps}](../../CDROM/refereed/629/img206.gif) |
![\includegraphics[width=60mm]{cucinaDistribution.eps}](../../CDROM/refereed/629/img207.gif) |
| (a) |
(b) |
Using the focus crawler described in [11], we have
performed two focus crawling sessions, downloading 150.000 pages for each
single crawl. During the first session the crawler spidered the Web searching
for pages on the topic ``Linux''. During the second session the crawler gathered
pages on ``cooking recipes''. Each downloaded page was classified to assess its
relevance with respect to the specific topic. Considering the
hyperlinks contained in each page, two Web subgraphs were created to
perform the evaluation of the different WPSSs proposed in the previous
sections. For the second crawling session, the connectivity map of pages
was pruned removing all links from a page to pages in the same site
in order to reduce the ``nepotism'' of Web pages.
The topological structure of the graphs and the scores of the text classifiers
were used to evaluate the following WPSSs:
- the ``In-link'' surfer. Such surfer is located in pages
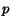 with
probability
with
probability
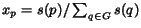 where
where 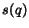 is the relevance
of the page computed by the text classifier;
is the relevance
of the page computed by the text classifier;
- the PageRank surfer;
- the Focused PageRank scheme as described in section
4.1;
- the Double Focused PageRank scheme described in section
4.2;
- the HITS surfer pool;
- the PageRank-HITS surfer pool.
We have performed an analysis of the distribution of page scores using the different
algorithms proposed in this paper. For all the PageRank surfers (focused or not)
we set the 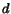 parameter equal to
parameter equal to 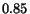 .
For each ranking function, we normalized the rank using its maximum
value. We sorted the pages according to their ranks,
then we plotted the distribution of the normalized rank values.
Figure 1 reports the plots for the two categories,
``Linux'' and ``cooking recipes''.
In both cases the HITS surfer assigns a score value significantly greater
than zero only to the small set of pages associated to the main eigenvector
of the connectivity matrix of the analyzed portion of the Web.
On the other hand the PageRank surfer is more stable and its score distribution
curve is smooth. This is the effect of the homogeneous term
.
For each ranking function, we normalized the rank using its maximum
value. We sorted the pages according to their ranks,
then we plotted the distribution of the normalized rank values.
Figure 1 reports the plots for the two categories,
``Linux'' and ``cooking recipes''.
In both cases the HITS surfer assigns a score value significantly greater
than zero only to the small set of pages associated to the main eigenvector
of the connectivity matrix of the analyzed portion of the Web.
On the other hand the PageRank surfer is more stable and its score distribution
curve is smooth. This is the effect of the homogeneous term 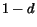 in
equation (17) and of the stability in the computation
provided by the probabilistic interpretation.
The Focused PageRank surfer and the Double Focused one still provide a smooth
distribution. However, the focused page ranks are more concentrated around
the origin. This reflects the fact that the vertical WPSSs are able to
discriminate the authorities on the specific topic, whereas the
classical PageRank scheme considers the authoritative pages regardless their topic.
in
equation (17) and of the stability in the computation
provided by the probabilistic interpretation.
The Focused PageRank surfer and the Double Focused one still provide a smooth
distribution. However, the focused page ranks are more concentrated around
the origin. This reflects the fact that the vertical WPSSs are able to
discriminate the authorities on the specific topic, whereas the
classical PageRank scheme considers the authoritative pages regardless their topic.

|

|
|
Figure 2:
We report the 8 top score pages from a portion of the
Web focused on the topic ``Linux'', using either the PageRank surfer,
or a HITS surfer pool.
For the HITS surfer pool we report the pages with the top authority value.
|
Figure 3:
We report the 8 top score pages from a portion of the
Web focused on the topic ``Linux'', using the proposed
focused versions of the PageRank surfer.
|
Figures 2 and 3 show, respectively,
the 8 top score pages
for four different WPSSs on the database with pages
on topic ``Linux'', while figures 4 and 5
reports the same results for the topic ``cooking recipes''.
As shown in figure 2,
all pages distilled by the HITS algorithm come from the same site.
In fact, a site which has many internal connections may acquire the
principal eigenvector of the connectivity matrix associated
to the considered portion of the Web graph, conquering all the top
positions in the page rank and hiding all other resources.
Even the elimination of intra-site links does not improve the performances of
the HITS algorithm. For example, as shown in the HITS section of
figure 4, the Web site ``www.allrecipe.com'',
which is subdivided into a collection of Web sites (``www.seafoodrecipes.com'',
``www.cookierecipes.com'', etc.) strongly connected among them, occupies all
the top positions in the ranking list, hiding all other resources.
In [10]
the content of pages is considered in order to propagate relevance scores
only over the subset of links pointing to pages on a specific topic.
In the ``cooking recipe'' case, the performances cannot be improved even
using page content, since all the considered sites are effectively on the
topic ``cooking recipes'', and then there is a semantic reason because such
sites are connected. We claim that such behavior is intrinsic of the HITS
model.

|

|
| Figure 4:
We report the 8 top score pages from a portion of the
Web, focused on the topic ``cooking recipes'', using either the
PageRank surfer, or the HITS surfer pool.
For the HITS surfer pool we report the pages with the top authority value.
|
Figure 5:
We report the 8 top score pages from a portion of the
Web, focused on the topic ``cooking recipes'', using the proposed
focused PageRank surfers.
|
The PageRank algorithm is not topic dependent. Since some pages are
referred to by many Web pages independently from their content, such pages
result in always being authoritative, regardless the topic of interest.
For example, in figures 2 and 4
pages like ``www.yahoo.com'', ``www.google.com'', etc, are shown
in the top list even if they are not closely related to the specific
topic.
It is shown in figures 3 and 5 that
the ``Focused PageRank'' WPSS described in section 4.1
can filter many off-topic authoritative pages from the top
list. Finally, the ``Double Focused PageRank'' WPSS
is even more effective in filtering all the off-topic
authorities, while pushing all the authorities on the relevant topic to
the top positions.
In order to evaluate the proposed WPSSs, we employed a
methodology similar to that one presented in
[12].
For each WPSS we selected the 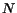 pages with highest score, creating a collection of pages to be evaluated
by a pool of humans.
pages with highest score, creating a collection of pages to be evaluated
by a pool of humans. 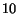 experts on the specific topics independently labelled
each page in the collection as ``authoritative for the topic'' or ``not
authoritative for the topic''.
Such a reliable set of judgments was finally used to measure the percentage of positive
(or negative) judgments on the best
experts on the specific topics independently labelled
each page in the collection as ``authoritative for the topic'' or ``not
authoritative for the topic''.
Such a reliable set of judgments was finally used to measure the percentage of positive
(or negative) judgments on the best 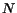 pages returned by each ranking function.
In particular,
pages returned by each ranking function.
In particular, 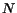 was varied between
was varied between 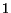 and
and 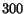 .
The topics selected for these experiments were ``Linux'' and ``Golf''.
As in the previous experiments 150.000 pages were collected by
focus crawling the Web.
.
The topics selected for these experiments were ``Linux'' and ``Golf''.
As in the previous experiments 150.000 pages were collected by
focus crawling the Web.
Figure 6 reports the percentage of
positive judgments on the 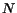 best pages returned by the five WPSSs,
respectively, for the topic ``Linux'' and ``Golf''.
In both cases the HITS algorithm is clearly the worst among the other ones.
Since its performance decreases significantly when applied to the entire
collection of documents, it can only be used as a query-dependent ranking
schema [1].
best pages returned by the five WPSSs,
respectively, for the topic ``Linux'' and ``Golf''.
In both cases the HITS algorithm is clearly the worst among the other ones.
Since its performance decreases significantly when applied to the entire
collection of documents, it can only be used as a query-dependent ranking
schema [1].
Figure 6:
The plots show the percentage of positive judgments assessed
by a set of 10 users on the best 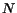 pages returned by the various WPSSs
respectively for the topic ``Linux'' (case a) and ``Golf'' (case b).
pages returned by the various WPSSs
respectively for the topic ``Linux'' (case a) and ``Golf'' (case b).
![\includegraphics[width=60mm]{linuxGoodLogToRes.eps}](../../CDROM/refereed/629/img216.gif) |
![\includegraphics[width=60mm]{golfGoodLogToRes.eps}](../../CDROM/refereed/629/img217.gif) |
| (a) |
(b) |
As previously reported in [12],
in spite of its simplicity the In-link algorithm has performances similar
to PageRank. In our experiments PageRank outperformed the
In-Links algorithm on the category ``Golf'', whereas it was outperformed on
the category ``Linux''. However, in both cases the gap is small.
The two focused ranking functions clearly outperformed all the not
focused ones, demonstrating that when searching focused authorities,
a higher accuracy is provided by employing a stable computation schema
and by taking into account the page content.
Conclusions
In this paper, we have proposed a general framework for the
definition of web page scoring systems for horizontal and
vertical search engines. The proposed scheme incorporates
many relevant scoring models proposed in the literature.
Moreover, it contains novel features which looks very appropriate
especially for vortals. In particular, the topological structure of the web
as well as the content of the web pages play jointly a crucial
rule for the construction of the scoring.
The experimental results support the effectiveness of the
proposal which clearly emerge especially for vertical search.
Finally, it is worth mentioning that the model described in
this paper is very well-suited for the construction of
learning-based WPSS, which can, in principle, incorporate the
user information while surfing the Web.
Acknowledgments
We would like to thank Ottavio Calzone who performed some
of the experimental evaluations of the scoring systems.
- 1
-
M. Henzinger, ``Hyperlink analysis for the Web,'' IEEE Internet
Computing, vol. 1, pp. 45-50, January/February 2001.
- 2
-
L. Page, S. Brin, R. Motwani, and T. Winograd, ``The PageRank citation
ranking: Bringing order to the web,'' tech. rep., Computer Science
Department, Stanford University, 1998.
- 3
-
J. Kleinberg, ``Authoritative sources in a hyperlinked environment.'' Report RJ
10076, IBM, May 1997, 1997.
- 4
-
K. Bharat and M. Henzinger, ``Improved algorithms for topic distillation in a
hyperlinked enviroment,'' in Proceedings of the 21st ACM SIGIR
Conference on Research and Developments in Information Retrieval,
pp. 104-111, 1998.
- 5
-
R. Lempel and S. Moran, ``The stochastic approach for link-structure analysis
(SALSA) and the TKC effect,'' in Proceedings of the 9th World Wide
Web Conference, 2000.
- 6
-
R. Lempel and S. Moran, ``Salsa: The stochastic approach for link-structure
analysis,'' ACM Transactions on Information Systems, vol. 19,
pp. 131-160, April 2001.
- 7
-
D. Cohn and H. Chang, ``Learning to probabilistically identify authoritative
documents,'' in Proc. 17th International Conf. on Machine Learning,
pp. 167-174, Morgan Kaufmann, San Francisco, CA, 2000.
- 8
-
D. Cohn and T. Hofmann, ``The missing link: a probabilistic model of document
content and hypertext connectivity,'' in Neural Information Processing
Systems, vol. 13, 2001.
- 9
-
E. Seneta, Non-negative matrices and Markov chains.
Springer-Verlag, 1981.
- 10
-
M. Joshi, V. Tawde, and S. Chakrabarti, ``Enhanced topic distillation using
text, markup tags, and hyperlinks,'' in International ACM Conference on
Research and Development in Information Retrieval (SIGIR), August 2001.
- 11
-
M. Diligenti, F. Coetzee, S. Lawrence, L. Giles, and M. Gori, ``Focus crawling
by context graphs,'' in Proceedings of the International Conference on
Very Large DataBases, 11-15 September 2000, Il Cairo, Egypt, pp. 527-534,
2000.
- 12
-
B. Amento, L. Terveen, and W. Hill, ``Does authority mean quality? predicting
expert quality ratings of Web documents,'' in Proceedings of the 23rd
International ACM SIGIR Conference on Research and Development in Information
Retrieval, pp. 296-303, 2000.
Footnotes
- ...
PageRank
- http://www.google.com
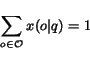
![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
![]() at time
at time ![]() ,
, ![]() . The probability
distribution on the pages of the Web is updated by taking into
account the possible actions at time
. The probability
distribution on the pages of the Web is updated by taking into
account the possible actions at time ![]() using the following
equation
using the following
equation
![]() .
These are
.
These are ![]() diagonal matrices defined as follows:
diagonal matrices defined as follows:
![]() whose diagonal values
whose diagonal values ![]() are the probabilities
are the probabilities ![]() ,
,
![]() collecting
the probabilities
collecting
the probabilities ![]() ,
,
![]() containing the values
containing the values ![]() , and
, and
![]() having on the diagonal the probabilities
having on the diagonal the probabilities ![]() .
.
![]() is the state transition matrix of
the Markov chain.
is the state transition matrix of
the Markov chain.
![]() is stable, since
is stable, since
![]() is a stochastic matrix having its maximum eigenvalue equal to
is a stochastic matrix having its maximum eigenvalue equal to ![]() .
Since the state vector
.
Since the state vector
![]() evolves following the equation
of a Markov Chain, it is guaranteed that if
evolves following the equation
of a Markov Chain, it is guaranteed that if
![]() , then
, then
![]() .
.

![\begin{displaymath}
\mathbf{\Sigma} = \left[
\begin{array}{cccc}
\frac{1}{N} & ...
...} & \frac{1}{N} & \ldots & \frac{1}{N} \\
\end{array} \right]
\end{displaymath}](../../CDROM/refereed/629/img64.gif)
![]() . Under these two assumptions,
equation (3) becomes
. Under these two assumptions,
equation (3) becomes
![]() ,
the solution of equation (7) is
,
the solution of equation (7) is
![]() different surfers,
we use a set of state variables
different surfers,
we use a set of state variables
![]() which represent
the probability of each surfer
which represent
the probability of each surfer ![]() to be visiting page
to be visiting page ![]() at time
at time
![]() . The interaction among the surfers is modeled by a set of
parameters which define the probability of the surfer
. The interaction among the surfers is modeled by a set of
parameters which define the probability of the surfer ![]() to accept
the suggestion of the surfer
to accept
the suggestion of the surfer ![]() , thus jumping from the page he/she
is visiting to the one visited by the surfer
, thus jumping from the page he/she
is visiting to the one visited by the surfer ![]() . This
interaction happens before the choice of the actions described previously.
If we hypothesize that the interaction does not depend on the
page the surfer
. This
interaction happens before the choice of the actions described previously.
If we hypothesize that the interaction does not depend on the
page the surfer ![]() is currently visiting, the degree of
interaction with the surfer
is currently visiting, the degree of
interaction with the surfer ![]() is modeled by the value
is modeled by the value
![]() which represents the probability for the surfer
which represents the probability for the surfer ![]() of jumping to
the page visited by the surfer
of jumping to
the page visited by the surfer ![]() . These values must satisfy the
probability normalization constraint
. These values must satisfy the
probability normalization constraint
![]() .
.
![]() , the novice,
blindly trusts the suggestions of surfer
, the novice,
blindly trusts the suggestions of surfer ![]() as he/she believes
as he/she believes
![]() is an expert in discovering authoritative pages,
whereas
is an expert in discovering authoritative pages,
whereas ![]() does not trust at all his/her own capabilities.
In this case the complete dependence of the novice on the expert
is modeled by choosing
does not trust at all his/her own capabilities.
In this case the complete dependence of the novice on the expert
is modeled by choosing ![]() and
and ![]() , i.e. the novice
chooses the page visited by the expert with probability equal to 1.
, i.e. the novice
chooses the page visited by the expert with probability equal to 1.
![]() repositions himself/herself
in page
repositions himself/herself
in page ![]() with probability
with probability
![]() looking at the
suggestions of the other surfers. This probability is computed
as
looking at the
suggestions of the other surfers. This probability is computed
as
![]() due to the action taken at time
due to the action taken at time ![]() by the surfer
by the surfer ![]() , we consider
the distribution
, we consider
the distribution
![]() instead of
instead of
![]() when
applying equation (2). Thus, the transition
function is defined as follows
when
applying equation (2). Thus, the transition
function is defined as follows
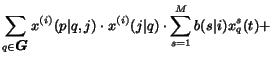
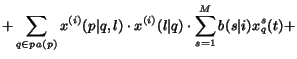
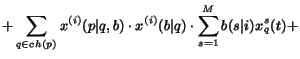
![]() surfers, the score vectors of each surfer
surfers, the score vectors of each surfer
![]() can be collected as the columns of a matrix
can be collected as the columns of a matrix
![]() .
Moreover, we define the
.
Moreover, we define the ![]() matrix
matrix
![]() which
collects the values
which
collects the values ![]() . The matrix
. The matrix
![]() will be referred to
as the interaction matrix. Finally, each surfer
will be referred to
as the interaction matrix. Finally, each surfer ![]() will be described by his/her own forward, backward and jump
matrices
will be described by his/her own forward, backward and jump
matrices
![]() ,
,
![]() ,
,
![]() and by the action matrices
and by the action matrices
![]() ,
,
![]() ,
,
![]() ,
,
![]() . Thus, the transition matrix for the Markov chain associated
to the surfer
. Thus, the transition matrix for the Markov chain associated
to the surfer ![]() is
is
![]() .
.
![]() interacting surfers can be described
by rewriting equation (14)
as a set of matrix equations as follows
interacting surfers can be described
by rewriting equation (14)
as a set of matrix equations as follows
![]()
![]() , and
, and
![]()
![]()
![]() ),
the model reduces to
),
the model reduces to ![]() models as described by
equation (6).
models as described by
equation (6).
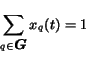
![]() ,
,
![]() for each page and then
equation (12)
guarantees that the Google's PageRank converges to a distribution
of page scores that does not depend on the initial distribution.
for each page and then
equation (12)
guarantees that the Google's PageRank converges to a distribution
of page scores that does not depend on the initial distribution.
![]() ,
, ![]() must be equal to
must be equal to ![]() and
and ![]() equal to
equal to ![]() . Thus, when there are sinks,
. Thus, when there are sinks,
![]() is defined as
is defined as
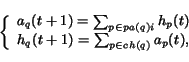
![]() and of jumping to a random page
and of jumping to a random page
![]() are null. Surfer 1 never follows a link, i.e.
are null. Surfer 1 never follows a link, i.e.
![]() whereas he/she always follows
a back-link, i.e.
whereas he/she always follows
a back-link, i.e.
![]() . Because of this, the
HITS computation violates the probability normalization constraints,
since
. Because of this, the
HITS computation violates the probability normalization constraints,
since
![]() .
.
![]() ,
and he/she never follows a back-link, i.e.
,
and he/she never follows a back-link, i.e.
![]() .
In this case the normalization constraint is violated for
the values of
.
In this case the normalization constraint is violated for
the values of ![]() because
because
![]() .
.
![]() , being
, being
![]() the identity matrix, whereas
the identity matrix, whereas
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() are
all equal to the null matrix.
are
all equal to the null matrix.
![]() matrix has a principal
eigenvalue much larger then
matrix has a principal
eigenvalue much larger then ![]() . Hence, unlike Google's PageRank, the HITS
algorithm needs the score to be normalized at the end of each iteration.
. Hence, unlike Google's PageRank, the HITS
algorithm needs the score to be normalized at the end of each iteration.
![]() , thus pushing
to zero the relevance of all other pages. As a result the page
scores tend to decrease rapidly to zero for pages outside those
communities. Recently some heuristics have been proposed to avoid this
problem even if such behavior can not be generally avoided because
of the properties of the dynamic system associated to the HITS algorithm
[10].
, thus pushing
to zero the relevance of all other pages. As a result the page
scores tend to decrease rapidly to zero for pages outside those
communities. Recently some heuristics have been proposed to avoid this
problem even if such behavior can not be generally avoided because
of the properties of the dynamic system associated to the HITS algorithm
[10].
![\begin{displaymath}
\mbox{\boldmath$A$}= \left[
\begin{array}{cc}
0 & 1 \\
1 & 0 \\
\end{array} \right]
\end{displaymath}](../../CDROM/refereed/629/img170.gif)
![]() and
and
![]() on the page
on the page ![]() . Hence, it holds that
. Hence, it holds that
![]() ,
,
![]() ,
where
,
where
![]() is the diagonal matrix with element
is the diagonal matrix with element ![]() equal to
equal to ![]() and
and
![]() is the diagonal matrix with element
is the diagonal matrix with element ![]() equal to
equal to ![]() . Then:
. Then:
![]() yields a normalized version
of HITS, which has been proposed in [4].
yields a normalized version
of HITS, which has been proposed in [4].
![]() and the pages linked by page
and the pages linked by page ![]() have scores
have scores
![]() by a topic
classifier, the probability of the surfer to follow the
by a topic
classifier, the probability of the surfer to follow the ![]() -th link
is defined as
-th link
is defined as
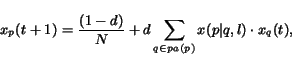
![]() of the current
page with respect to the target, i.e.
of the current
page with respect to the target, i.e.
![]() , i.e.
, i.e.
![\includegraphics[width=60mm]{linuxDistribution.eps}](../../CDROM/refereed/629/img206.gif)
![\includegraphics[width=60mm]{cucinaDistribution.eps}](../../CDROM/refereed/629/img207.gif)
![]() best pages returned by the five WPSSs,
respectively, for the topic ``Linux'' and ``Golf''.
In both cases the HITS algorithm is clearly the worst among the other ones.
Since its performance decreases significantly when applied to the entire
collection of documents, it can only be used as a query-dependent ranking
schema [1].
best pages returned by the five WPSSs,
respectively, for the topic ``Linux'' and ``Golf''.
In both cases the HITS algorithm is clearly the worst among the other ones.
Since its performance decreases significantly when applied to the entire
collection of documents, it can only be used as a query-dependent ranking
schema [1].
![\includegraphics[width=60mm]{linuxGoodLogToRes.eps}](../../CDROM/refereed/629/img216.gif)
![\includegraphics[width=60mm]{golfGoodLogToRes.eps}](../../CDROM/refereed/629/img217.gif)