Simulation, Verification and Automated Composition

of Web Services

 

 

ABSTRACT

Web services -- Web-accessible programs and devices – are a key application area for the Semantic Web. With the proliferation of Web services and the evolution towards the Semantic Web comes the opportunity to automate various Web services tasks.  Our objective is to enable markup and automated reasoning technology to describe, simulate, compose, test, and verify compositions of Web services.  We take as our starting point the DAML-S DAML+OIL ontology for describing the capabilities of Web services.  We define the semantics for a relevant subset of DAML-S in terms of a first-order logical language.  With the semantics in hand, we encode our service descriptions in a Petri Net formalism and provide decision procedures for Web service simulation, verification and composition.  We also provide an analysis of the complexity of these tasks under different restrictions to the DAML-S composite services we can describe.  Finally, we present an implementation of our analysis techniques.  This implementation takes as input a DAML-S description of a Web service, automatically generates a Petri Net and performs the desired analysis.  Such a tool has broad applicability both as a back end to existing manual Web service composition tools, and as a stand-alone tool for Web service developers.

Categories and Subject Descriptors

I.2.4 [Artificial Intelligence]:  Knowledge Representation Formalisms and Methods - Representation languages, representations, Predicate logic, Frames and scripts.

General Terms

Algorithms, Design, Standardization, Languages, Theory,  Verification.

Keywords

Semantic Web, DAML, Ontologies, Web Services, Web Service Composition, Distributed Systems, Automated Reasoning.

 

1.  INTRODUCTION

The vision of the semantic Web [4] is to provide computer-interpretable markup of the Web’s content and capability, thus enabling automation of many tasks currently performed by human-beings.  A key application for semantic Web technologies is Web services – Web-accessible programs and devices that will proliferate the Web.   Examples of such Web services include the book-buying service at www.amazon.com, or the travel service at www.travelocity.com.  Semantic markup of the content and capability of Web services – what a service does, how to use it, what its effect will be – will enable easy automation of a variety of reasoning tasks, currently performed manually by human beings, or through arduous hand-coding that enables subsequent automation.  Such tasks include automated Web service discovery, automated invocation, automated interoperation, automated selection and composition, and automated execution monitoring [10,17,23].

 

In this paper, we are motivated by issues related to Web service composition.  Compositions of Web services are created in many different ways.  Many compositions are created manually by the service provider by taking simple Web-accessible programs, such as a form-validation program, or database lookup program, and composing them using typical procedural programming constructs such as if-then-else, sequence or while-loop.   The book-buying service at www.amazon.com is an example of a composite service.

 

A number of software systems are available to facilitate manual composition of programs, and more recently Web services.  Such programs, which include a diversity of workflow tools [1,12], and more recently service composition aids such as BizTalk Orchestration [20] enable a user to manually specify a composition of programs to perform some task.  Most recently, technologies have been proposed that use some form of semantic markup of Web services in order to automatically compose Web services to perform some desired task (e.g., [23,24,3,31]).  Regardless of how the compositions originated, we are interested here in describing and proving properties of these services – to test the system by simulating its execution under different input conditions, to logically verify certain maintenance and safety conditions associated with the service, and to automatically compose services.  In summary, our objective is to enable markup and automated reasoning technology to describe, simulate, automatically compose, test and verify Web service compositions. 

 

Our starting point is the DAML-S ontology for Web services [8,9], which we exploit to provide semantic markup of the content and capabilities of Web services.  In Section 3 we provide a semantics for a portion of the DAML-S language we require to describe compositions of Web services.  In Section 4, we provide an operational semantics using Petri Nets.  In Section 5, we describe decision procedures for Web services simulation, testing, composition, and verification.  We also provide an analysis of the complexity of these tasks under restricted classes of Web service compositions.  Finally in Section 6, we discuss our implementation of a software tool for performing the proposed automated reasoning tasks.  The theory and implementation presented in this paper has broad applicability both as a back end to enhance existing manual composition tools, and as a stand-alone tool for simulation, testing, verification and automated composition of Web services.

 

2.  DAML-S

Critical to the vision of the semantic Web is the provision of a markup language, (or in artificial intelligence (AI) terminology, a knowledge representation language), that has a well-defined semantics to enable unambiguous computer interpretation.  The language must also be sufficiently expressive to describe the properties and capabilities of Web services.  Over the last several years, a number of semantic Web markup languages have been proposed.  These include XML, RDF and RDF(S) and most recently DAML+OIL [13,17,30].  We have adopted DAML+OIL as our content language for describing Web services, and in particular we have adopted DAML-S.

 

DAML+OIL is an AI-inspired description logic-based language for describing taxonomic information. The DAML+OIL language builds on top of XML and RDF(S) to provide a language with both a well-defined semantics and a set of language constructs including classes, subclasses and properties with domains and ranges, for describing a Web domain.  DAML+OIL can further express restrictions on membership in classes and also restrictions on domains and ranges, including cardinality restrictions. 

 

DAML-S is a DAML+OIL ontology for Web services developed by a coalition of researchers[3], under the auspices of the DARPA Agent Markup Language (DAML) program.  The latest release of this ontology is located at [8] and an earlier version is described [9]. The DAML-S ontology describes a set of classes and properties, specific to the description of Web services.  The upper ontology of DAML-S comprises the service profile for describing service advertisements, the process model for describing the actual program that realizes the service, and the service grounding for describing the transport-level messaging information associated with execution of the program.  The service grounding is akin to the Web Service Description Language, WSDL.

 

It is the process model that provides a declarative description of the properties of the Web-accessible programs we wish to reason about. To illustrate the salient features of the DAML-S process model, we use the example of a fictitious book-buying service offered by the Web service provider, Congo Inc.  The Congo example was described in the original release of DAML-S, and its markup can be found at http://www.daml.org/services.  We use a variant of it here for illustration purposes.

 

The process model conceives each program as either an atomic  or composite process. It additionally allows for the notion of a simple process, which is used to describe a view, abstraction or default instantiation of the atomic or composite process to which it expands. We focus here on atomic and composite processes.

 

<daml:Class rdf:ID="Process">

  <daml:unionOf rdf:parseType="daml:collection">

    <daml:Class rdf:about="#AtomicProcess"/>

    <daml:Class rdf:about="#SimpleProcess"/>

    <daml:Class rdf:about="#CompositeProcess"/>

  </daml:unionOf>

</daml:Class>

An atomic process is a non-decomposable Web-accessible program.  It is executed by a single (e.g., http) call, and returns a response.  It does not require an extended conversation between the calling program or agent, and the Web service. 

 

<daml:Class rdf:ID="AtomicProcess">

  <daml:subClassOf rdf:resource="#Process"/>

</daml:Class>

An example of an atomic process is the LocateBook service that takes as input the name of a book and returns a description of the book and its price, if the book is in Congo’s catalogue.

 

<daml:Class rdf:ID="LocateBook">

  <rdfs:subClassOf 

          rdf:resource="&process;#AtomicProcess"/>

</daml:Class>

 

In contrast, a composite process is composed of other composite or atomic processes through the use of control constructs.  These constructs are typical programming language constructs such as sequence, if-then-else, while, fork, etc. that dictate the ordering and the conditional execution of processes in the composition.  We provide a subset of the markup below.

 

<daml:Class rdf:ID="CompositeProcess">

 <daml:intersectionOf

            rdf:parseType="daml:collection">

   <daml:Class rdf:about="#Process"/>

   <daml:Restriction daml:minCardinality="1">

     <daml:onProperty rdf:resource="#composedOf"/>

   </daml:Restriction>

 </daml:intersectionOf>

</daml:Class>

 

<rdf:Property rdf:ID="composedOf">

  <rdfs:domain rdf:resource="#CompositeProcess"/>

  <rdfs:range rdf:resource="#ControlConstruct"/>

</rdf:Property>

 

An example of a composite process might be the Find-n-Buy service that composes LocateBook, together with order request and financial transaction services.  The composition constructs allow for multiple different execution pathways to termination depending, in this case, on whether the book is sold by Congo, is in stock, and whether the user wishes to buy it.

 

Associated with each process is a set of properties. Using a program or function metaphor, a process has parameters to which it is associated.  Two types of parameters are the DAML-S properties input and (conditional) output.

 

<rdf:Property rdf:ID="parameter">

 <rdfs:domain rdf:resource="#Process"/>

 <rdfs:range 

   rdf:resource="http://www.daml.org/... #Thing"/>

 </rdf:Property>

 

<rdf:Property rdf:ID="input">

 <rdfs:subPropertyOf rdf:resource="#parameter"/>

</rdf:Property>

An input for LocateBook might be the name of the book.

<rdf:Property rdf:ID="bookName">

  <rdfs:subPropertyOf

             rdf:resource="&process;#input"/>

  <rdfs:domain rdf:resource="#LocateBook"/>

  <rdfs:range rdf:resource="&xsd;#string"/>[4]

</rdf:Property>

 

Inputs can be mandatory or optional.  In contrast, outputs are generally conditional.  This is important.  For example, when you search for a book in the Congo catalogue, the output may be a detailed description of the book, if Congo carries it, or it may be a “Sorry we don’t carry.” message.  Such outputs are characterized as conditional outputs. We define a conditional output class that describes both a condition and the output based on this condition.  An unconditional output has a zero cardinality restriction on its condition.

 

<rdf:Property rdf:ID="output">

 <rdfs:domain rdf:resource="#parameter"/>

 <rdfs:range rdf:resource="#ConditionalOutput"/>

</rdf:Property>

 

<daml:Class rdf:ID="ConditionalOutput">

 <daml:subClassOf

    rdf:resource="http://www.daml.org/...#Thing"/>

</daml:Class>

 

<rdf:Property rdf:ID="coCondition">

  <rdfs:comment>

     The condition of the conditional output.

  </rdfs:comment>

<rdfs:domain rdf:resource="#ConditionalOutput"/>

 <rdfs:range rdf:resource="#Condition"/>

</rdf:Property>

 

<rdf:Property rdf:ID="coOutput">

  <rdfs:comment>

     The output of the conditional output.

  </rdfs:comment>

  <rdfs:domain rdf:resource="#ConditionalOutput"/>

  <rdfs:range 

    rdf:resource="http://www.daml.org/...#Thing"/>

</rdf:Property>

 

In addition to the program or function metaphor, it is also useful to use an action, event or process metaphor to conceive services.  In this context we can consider services to have the properties precondition and (conditional) effect.  Preconditions and conditional effects are described analogously to inputs and conditional outputs.

 

Preconditions specify things that must be true of the world in order for an agent to execute a service.  A precondition of every process is that the agent knows the input parameters of the process.  For example, one precondition for LocateBook is that the agent Knows(bookName). Stipulating knowledge preconditions pertaining to the input parameters is redundant with the input parameters and are only distinguished as knowledge preconditions in the semantics.  Many Web services that are embodied as programs on the Web only have these preconditions.  At the level of abstraction we are modeling Web services, there are no physical preconditions to the execution of a piece of software on the Web.  In contrast, Web-accessible devices may have many physical preconditions such as bandwidth resources or battery power. 

 

<rdf:Property rdf:ID="precondition"> 

<rdfs:domain rdf:resource="#Process"/>

<rdfs:range 

   rdf:resource="http://www.daml.org/... #Thing"/>

</rdf:Property>

 

Conditional effects characterize the physical side-effects, execution of a Web-service has on the world.  An example of a conditional effect for a BuyBook service might be Own(bookName), when InStock(bookName).  Note that not all services have physical side-effects, in particular, services that are strictly information providing do not.  The DAML-S markup for conditional effects is analogous to that for conditional outputs.

 

3.  THE SEMANTICS OF DAML-S

The DAML-S DAML+OIL ontology provides a set of distinguished classes and properties for describing the content and capabilities of Web services.  The DAML+OIL language in which it is specified has a well-defined semantics, however the expressive power of DAML+OIL is not sufficient to restrict DAML-S to all and only the intended interpretations.  Our objective in this section is to describe a semantics for that portion of DAML-S that is relevant to our work on Web service composition.  In particular, we ascribe a semantics to the notion of atomic and composite processes.

 

One compelling way to do this, as has been done with the semantics of DAML+OIL [13], is to describe DAML-S in a more expressive language, such as first-order logic, and to add a set of axioms to this theory that constrains the models of the theory to all and only the intended interpretations.  Since DAML-S is actually a process modeling language, and its relationship to other process modeling languages is important to interoperability, an even more compelling way to ascribe a semantics to DAML-S is to map it to the US National Institute of Standard’s (NIST) Process Specification Language (PSL) [29].  PSL is a process specification ontology described in the situation calculus, a (mostly) first-order logical language for reasoning about dynamical systems [28].  PSL’s role is to serve as the lingua franca for all business and manufacturing process specification languages. Once the DAML-S language is stabilized, we should easily be able to translate the situation calculus description in Section 3.1 into the PSL ontology [15]. 

 

3.1  From DAML-S to Situation Calculus

The situation calculus language we use [28] is a first-order logical language for representing dynamically changing worlds in which all of the changes are the direct result of named actions performed by some agent.  Situations are sequences of actions, evolving from an initial distinguished situation, designated by the constant S₀.  If a(y)[5] is an action and s, a situation, the result of performing a in s is the situation represented by the function do(a,s).  Functions and relations whose values vary from situation to situation, called fluents, are denoted by a predicate symbol taking a situation term as the last argument (e.g., Own(bookName,s)).  Finally, Poss(a,s) is a distinguished fluent expressing that action a is possible to perform in situation s.  

 

The dialect of the situation calculus that we use includes a means of representing knowledge.  In particular, there is a distinguished fluent K(s,s’) that describes the accessibility relation between situations. The notation Knows(f,s) denotes that the formula f is known in situation s (e.g., Knows(Owns(“On the Road”,s))). The notation Kwhether(f,s) is an abbreviation for a formula indicating that the truth value of f is known.  I.e., Kwhether(f,s) = Knows(f,s) Ú Knows(Øf,s).  Finally, the abbreviation Kref(j,s) abbreviates a formula indicating that the functional value of j is known.  The situation calculus is fully described in [28].  We dispense with further details and focus here on the salient features relevant to this paper.

 

Atomic processes in DAML-S are actions a(y) in the situation calculus.  The input parameters of an atomic process are the parameters y of action a. E.g., the atomic process BuyBook is the parameterized action BuyBook(bookName) .

 

Conditional effects and outputs:  The conditional effects of an atomic process are represented in the situation calculus as positive and negative effect axioms of the following form:

     Poss(a,s) Ù g_F⁺(x,a,s)  ® F(x,do(a,s))

     Poss(a,s) Ù g_F^-(x,a,s)  ®  Ø F(x,do(a,s)).

 

g_F^(+/-)(x,a,s) contains all the different combinations of actions and conditions that would make fluent F (e.g., Own(bookName,s)) respectively true/false after execution of the action. The following is an example of a positive effect axiom for the BuyBook service with respect to its effect on Own(bookName).  In this example, g_F⁺(x,a,s) is a=BuyBook(bookName) Ù Instock(bookName).

      Poss(a,s) Ù  a=BuyBook(bookName)  Ù  Instock(bookmane,s)

                                                              ® Own(bookName,do(a,s))

 

In our example, we do not illustrate a service that has a negative effect on the fluent Own. To make it more interesting, we add the following.

     Poss(a,s) Ù  a=SellBook(bookName)

                                                        ® Ø Own(bookName,do(a,s))

Although specified as outputs rather than effects in the DAML-S markup, the conditional outputs of an atomic process a are treated as knowledge effects semantically.  This is an important distinction captured in our semantics.  E.g.,

    Poss(a,s)  Ù

        a=LocateBook(bookName)   Ù  Incatalogue(bookName,s)

                                                  ®  Kref(Price(bookName),do(a,s))

 

The output of a service is the information the agent is being told.  Hence the effect will either be a Kref, Kwhether or Knows expression.

 

To address the frame problem representationally [28], effect axioms are compiled into successor state axioms, by appealing to a causal completeness assumption – that the effect axioms for a fluent F characterize all and only actions that cause a change in the (truth) value of fluent F.  Successor state axioms express all the conditions underwhich a fluent value can change.  This ensures that the models of the situation calculus represent all and only the intended interpretations.

 

Successor state axioms, one for each fluent in the language, are of the following form:

     F(x,do(a,s)) º g_F⁺(x,a,s) Ú (F(x,s) Ù  Ø g_F^-(x,a,s))

I.e., the fluent F is true in do(a,s) iff an action made it true (i.e., g_F⁺(x,a,s)) or it was already true and an action did not make it false (i.e., (F(x,s) Ù  Ø g_F^-(x,a,s))).

     Own(bookName,do(a,s)) º 

(a=BuyBook(bookName)  Ù Instock(bookName,s))

              Ú  (Own(bookName,s) Ù a ¹ SellBook(bookName))

 

Successor state axioms for knowledge are discussed in [28].

 

Preconditions and inputs:  DAML-S preconditions for an atomic process are represented as well-formed formula in the situation calculus.  Each precondition of an atomic process is expressed as a necessary condition for actions in the situation calculus.

     Poss(a,s)   ® p_i

where p_i  is a formula relativized to s.  E.g.,

     Poss(CheckGPS(location),s) ® Charged(GPSbattery,s)

 

For multiple preconditions, this generalizes to:

     Poss(a,s)   ® p₁ Ù p₂ Ù¼Ù p_n

 

Just as outputs are treated as knowledge effects, so too are inputs treated as knowledge preconditions semantically.  The agent must know the value of the inputs to the service before it can execute the service. For example, in order to execute LocateBook, the agent must know the values of all the inputs.  Hence for every input j_i, of an atomic process a,

     Poss(a,s) ®  Kref(j₁,s) Ù¼Ù Kref(j_n,s)

 

Under the completeness assumption, that the preconditions encode all and only the preconditions for an atomic process, these necessary conditions for action are compiled into action precondition axioms of the following form:

     Poss(a,s) º p₁ Ù p₂ Ù¼Ù p_n Ù Kref(j₁,s) Ù¼Ù Kref(j_n,s)

 

E.g.,

     Poss(CheckGPS(location),s) º

                                      Charged(GPSbattery,s) Ù Kref(location,s)

 

The complete situation calculus axiomatization of a DAML-S description includes the sets of axioms described above,

·          successor state axioms, D_SS,

·          action precondition axioms, D_ap,,

as well as the following axioms described in [28], namely

·          foundational axioms of the situation calculus, S,

·          axioms describing the initial situation, D_S0,,

·          unique names for actions, D_una,

·          domain closure axioms for actions, D_dca.

 

These axioms collectively capture the intended interpretation of the portion of DAML-S we have described here.

 

Note that we have not described the translation of DAML-S composite processes into the situation calculus.  This translation follows nicely from the representation of complex actions in the situation calculus using Golog [14]. Further discussion of this point is beyond the scope of this paper.

 

4.  AN OPERATIONAL SEMANTICS

In the previous section we ascribed a semantics to a relevant subset of DAML-S.  With this semantics in hand, we can reason about the execution of Web services.  We use the situation calculus as a lingua franca and translate into a representation that provides special-purpose machinery for the tasks we wish to address.  Specifically, we use the distributed operational semantics of processes provided by Petri Nets [26].  Several other options present themselves, including simple finite state automata, or process algebras such as the Pi-Calculus.  The latter provides the theoretical foundations for Microsoft’s XLANG.  However, most of these approaches do not offer techniques for quantitative analysis. We selected Petri Nets for its combination of compelling computational semantics, ease of implementation, and its ability to address both offline analysis tasks such as Web service composition and online execution tasks such as deadlock determination resource satisfaction, and quantitative performance analysis.  We also note the existence of several well-known techniques mapping from Petri Nets to process logics and vice versa [25,26].

 

There are tradeoffs associated with any choice of computational machinery.  In the most general case, Petri Nets with inhibitory arcs are Turing equivalent.  Hence, the translation from situation calculus does not limit the systems we can analyze.  Nevertheless, the situation calculus is a more parsimonious for large theories.  Petri Nets have a form of computational completion semantics that enables easy mapping from the situation calculus and that addresses the frame problem in a very nice way [27]. Their natural representation of change and concurrency allows us to construct a distributed and executable operational semantics of Web services. We are also able to bring to bear well established theories from the vast computer science literature on Petri Nets [26] to define subclasses of the DAML-S process model with respect to their computational complexity. Finally, Petri Nets also have the advantage of dealing with resources, something that will be important in reasoning about Web service devices.

 

In the subsection to follow we describe our approach in detail.  We introduce the notion of a Petri Net and describe the representation of our situation calculus theory in Petri Nets.  We then go on to describe computational analysis techniques to realize many Web service automation tasks. 

 

4.1  Petri Nets

We have constructed an execution semantics for DAML-S based on Petri Nets. A Petri Net is a bipartite graph containing places (drawn as circles) and transitions (drawn as rectangles).  Places hold tokens and represent predicates about the world state or internal state. Transitions are the active component.  When all of the places pointing into a transition contain an adequate number of tokens (usually 1) the transition is enabled and may fire, removing its input tokens and depositing a new set of tokens in its output places.  The most relevant features of Petri Nets for our purposes are their ability to model events and states in a distributed system and to cleanly capture sequentiality, concurrency and event-based asynchronous control. Our extensions to the basic Petri Net formalism include typed arcs, hierarchical control, durative transitions, parameterization, typed (individual) tokens and stochasticity. For this paper, the crucial fact about our representation is that it is active with a well defined real-time execution semantics for service descriptions.

 

The rest of this section details our mapping.  The section to follow describes our automatic model construction, simulation and analysis of DAML-S markups using the theory of Petri Nets. While we are aiming for this paper to be selfsufficient, we will borrow results from the well-developed theory of concurrent systems. For specific relevant results, we refer the reader to the appropriate citation. For a more general introduction to the theory and analysis of distributed and concurrent systems using Petri Nets, the reader is referred to one of several excellent surveys (e.g., [26, 5, 32,1]).

 

Definition 1 (Petri Nets) A Petri Net (PN) is an algebraic structure (P, T, I, O) composed of:

·          finite set  of places, P = {p1, p2, ... pn},

·          finite set of transitions, T = {t1, t2, ... tm},

·          Transition Input Function, I. I maps each transition ti to a multiset of P.

·          Transition Output Function, O. O maps each transition ti to a multiset of P. [6]

 

Definition 2 (Markings/Tokens/Initial marking) A marking in a Petri Net PN(P, T, I, O) is a function µ, that maps every place into a natural number. If for a given marking µ, µ(pi) = x, then it is said that the place pi holds x tokens at the marking µ. A special marking, denoted by µ0, will be called the initial marking.

 

Definition 3 (Enabled/Fireable transitions at marking µ) At a given marking µ, if for any ti e T, µ(p) ³ #[p,I(ti)], " p e P, then ti is said to be enabled by the marking µ.  Here #[p,I(ti)] denotes the number of occurrences of place p in the multiset I(ti). Let us denote the set of all enabled transitions at a given marking µ by EN(µ).  In conventional Petri Nets every enabled transition may fire. This is not always true for other kind of Petri Nets, particularly the timed ones.  If we denote by F(µ) the set of all fireable transitions at a given marking µ, then for conventional Petri Nets F(µ) = EN(µ).

 

Definition 4 (Transition firing/Occurrence sequence)  The firing of any enabled transition, ti, at marking µ, causes the change of the marking µ to a new marking µ' as follows: " p e P, µ'(p) = µ(p) - #[p,  I(ti)] + #[p, O(ti)].  Where: #[p, I(ti)] and #[p, O(ti)], denotes, the number of occurrences of place p in the multiset I(ti) and in the multiset O(ti) respectively. In other words, the new marking µ', for each place p, is equal to the old number of tokens in that place, minus the number of occurrences of p in the input.  A sequence of firings (t1 …tn) that take an initial marking µ0 to a new marking µN is called an occurrence sequence.

 

Graphical representation:  The algebraic structure of a Petri Net PN(P, T, I, O) may be represented graphically. In this graphical representation, a Petri Net will be represented by a bipartite graph, where:  every place will be represented by a circle; every transition will be represented by a rectangle ; the function I will be represented by directed arcs linking every p Î I(ti) to the transition ti. These arcs are called input arcs to the transition ti; and the function O will be represented by directed arcs linking each transition ti to every p Î O(ti). Analogously with the input arcs, these arcs are called output arcs to the transition ti .

 

Modeling discrete systems with Petri Nets:  When modeling a discrete system with a Petri Net, partial states of the system are represented by places. Whether the system is in a particular partial state or not is represented by the presence/absence of a token in the place representing this partial state. Events are represented by the transitions. Conditions allowing an event to occur are represented by the input arcs to the associated transition of this event. These are normally called pre-conditions. The input places of these arcs represent the combination of the several partial states that must be valid in order that the event represented by the transition occurs. After the occurrence of an event (firing of an enabled transition) a new set of partial states will be valid. These are called the post conditions and are represented by the output arcs of the fired transition.

 

4.2  A Petri Net Semantics for DAML-S

Section 3 defined the semantics of DAML-S atomic processes in terms of a set of situation calculus axioms. We start by showing the mapping from the situation calculus axioms to the corresponding Petri Net structure. After describing the basic mapping, we describe the net structures for the various control constructs that define composite processes in DAML-S.

 

4.2.1  DAML-S Atomic Processes as Petri Nets

Recall, the basic set of axioms representing the DAML-S atomic process were the effect axioms, i.e.,

     Poss(a,s) Ù g_F⁺(x,a,s)  ® F(x,do(a,s))

     Poss(a,s) Ù g_F^-(x,a,s)  ® ØF(x,do(a,s)),

 

and the necessary conditions for actions.  The latter embody both the physical preconditions described in the DAML-S markup, and the knowledge preconditions reflecting the requirement that an agent know the values of the input parameters of the process.  We distinguish these by the subscript w (world) and k (knowledge) :

     Poss_w (a,s) ® p₁ Ù p₂ Ù¼Ù p_n

     Poss_k(a,s) ®  Kref(j₁,s) Ù¼Ù Kref(j_n,s)

     Poss(a,s) ® p₁ Ù p₂ Ù¼Ù p_n Ù Kref(j₁,s) Ù¼Ù Kref(j_n,s)

 

In the situation calculus, a completion assumption is made to reflect that 1) the effect axioms specify all and only the conditions under which a fluent can change, and 2) the necessary conditions for actions specify all and only the conditions under which an action a is possible to execute.  This completion assumption is captured axiomatically by translating effect axioms into successor state axioms and necessary conditions for actions into action precondition axioms.  Petri Nets provide a computational mechanism for achieving this completion.  The graph structure defines the completion and computation over the graph structure achieves the computational completion semantics.  Hence, the solution to the frame problem is captured in the computational semantics of Petri Nets.

 

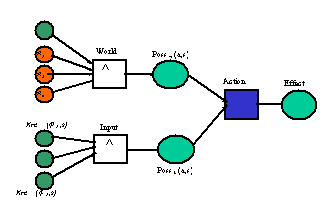
Figure 1.  Atomic DAML-S process

 

 

Figure 1 illustrates the graphical Petri Net representation of a DAML-S atomic process.  With multiple conditional effects, there would be a transition for each possible conditional effect, with a preset of the specific condition(s) and a postset of the effect of excecuting that action under those conditions. To ease exposition in this paper, we will not consider multiple conditional effects. In the discussion to follow, the atomic process in Figure 1 will be represented as a single transition (in blue, where visible).

4.2.2  DAML-S Composite Processes as Petri Nets

Having illustrated the mapping from the situation calculus description of a DAML-S atomic process, we now turn to modeling composite processes as Petri Net structures.   DAML-S composite processes are compositions of sub-processes -- other composite or atomic processes. All composite processes bottom out in atomic processes.  The DAML-S composedOf property specifies the control flow and data flow of its sub-processes, yielding constraints on the ordering and conditional execution of these sub-processes.

 

 

 

 

 

 

 

 

 

 

 

Figure 2.  Canonical DAML-S composite process

 

Figure 2 illustrates the canical graphical Petri Net representation of a DAML-S composite process, comprising start/finish, ready/done, and a control construct. We consider each construct of DAML-S version 0.6 [8] and provide the appropriate Net structure that captures a possible execution semantics of that construct. The basic control constructs we consider are the sequence, parallel, condition, choice, and the various iterate classes of DAML-S. Figure 3 depicts the Distributed OPErational (DOPE) semantics for the various DAML-S composite constructs.

 

We have implemented a DAML-S interpreter that translates DAML-S markups to the Petri Net based simulation and modeling environment KarmaSIM [27]. The KarmaSIM tool allows for interactive simulation and supports the various verification and performance analysis techniques. In Figure 3, the thickened (red, where visible) arcs correspond to the result of transition firing and token transfer as the system moves from state to state. The thickened (brown filled) transitions depict the enabled transitions. As is clear from the state shown in Figure 3, the overall system has a distributed operational semantics.  I.e., each transition fires based on its local input conditions, and transition firings correspond to system evolution.

 

We now describe the various DAML-S composite constructs and their DOPE semantics. Note that in Figure 3, DAML-S atomic processes correspond to transition and embedded composite processes are recursively built up from their ground atomic processes.  In Section 6, we illustrate a book buying example [8] that utilizes and illustrates many of these constructs. 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

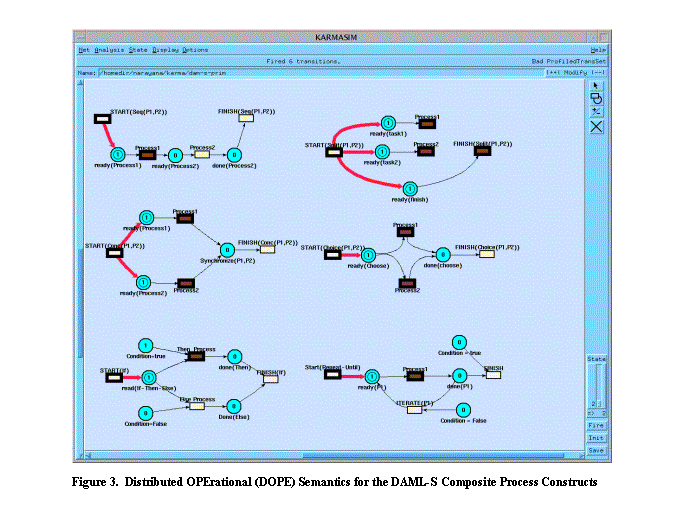
The sequence construct:  In DAML-S, Sequence has a list of component sub-processes that specify the body. As shown in Figure 3 (Seq(P1,P2)), the semantics of sequence is a total ordering on the process list, where Process1 (P1) and Process2 (P2) are executed in sequence.  Assuming its preconditions are satisfied, P2 can execute  upon the completion of P1.

 

The split construct:  A split composite process consists of concurrent execution of a bag of sub-processes.  No further specification about waiting, synchronization, etc. is made at this level of the DAML-S ontology. Our model of the Split construct assumes a process that initiates a set of concurrent processes and terminates. We use special constructs to model the synchronization aspects, both local and barrier types. Thus, in the situation shown in Figure 3 (Split(P1,P2)), the two split processes Process1 and Process2 are initiated, and the composite process is ready to transition to a FINISHed state.

 

The split and join (concurrent) construct:  A split-and-join composite process consists of concurrent execution of a bag of sub-processes. The default assumes barrier synchronization. With Split and Split and Join, we can define processes which have partial synchronization (e.g., split all and join some subset). In the example network shown in Figure 3 (Conc(P1,P2)), both processes are concurrently enabled and the overall composite process waits until both processes are completed. One can analogously construct cases of Split n join m (m <= n), etc.

The choice construct: A choice composite process selects a process for execution from among a bag of processes. The choose property, takes a choice bag and returns a chosen bag. The cardinality of the bag can be specified through a restriction to get choose(n)  (0<n<=|bag|). DAML-S does not distinguish choice from alternative.  As shown in Figure 3 (Choice(P1,P2)), the DAML-S specification corresponds to both Process1 and Process2 being possible choices; selecting and completing either choice would allow the composite process to finish.  The semantic framework supports probabilistic choice, but DAML-S has not (yet) been augmented with probabilities.

 

The if-then-else construct:  An if-then-else composite process is a simple construct that has a relation whose domain is a process and whose range is a binary value. This internal process usually  corresponds to one or more test actions, but it may alternatively be some evaluation of world state, resource levels, timeouts or other conditions that affect the evolution of processes.  DAML-S conditions have a property conditionValue which is a boolean. The specific execution branch (i.e., which process/action to execute) depends on the value of this property.  In the example shown in Figure 3 (If-Then-Else), the Condition value is TRUE and the Then branch of the If-Then-Else is enabled. If the Condition value were FALSE, the Else process bag would be active.

 

The repeat-condition construct: DAML-S has both repeat-while and repeat-until composite processes.  Repeat-while specializes the ControlConstruct class with properties whileCondition (whose DAML-S range is of type Condition) and whileProcess (range is of type Repeat).  No commitments are made about whether this is asynchronous (w/o prioritized interrupts) or synchronous (with specific polling/busy-wait strategies), etc.  This is left for the particular execution model to specify.  Similarly, repeat-until specializes the ControlConstruct class with properties untilCondition (range is of type Condition) and untilProcess (range is of type Repeat).  Figure 3 (repeat-until) shows the execution semantics of the Repeat-until construct. The Repeat-while semantics is analogous except that input places for the DAML-S conditionValue (the Condtion=true and Condition=False nodes in Figure 3) are reversed.

5.  ANALYSIS OF WEB SERVICES TASKS

Whether created manually by Web service providers, value-adding 3^rd party Web service providers, or by some automated tool, the semantic Web will be replete with composite services.  Assessing the correctness, effectiveness, safety and efficiency of composite services is vital to safe and reliable automation of Web services.  In this section we provide a set of computational analysis tools, based on our Petri Net representation, that enable us to automate Web service tasks such as:

Simulation – simulate the evolution of a Web service under different conditions.

Validation – test whether a Web service behaves as expected.

Verification – establish the upholding of certain properties of a Web service (e.g., that it maintains certain properties, that it ensures safety, etc.)

Composition – generate a composition of Web services that achieves a specified goal.

Performance Analysis – evaluate the ability of a service to meet requirements with respect to throughput times, service levels, and resource utilization.

 

While our tools provide for sophisticated performance analysis, detailed discussion of these techniques is outside the scope of this paper. In Section 6, we discuss the implementation of these analysis tools together with their application to DAML-S described Web services.

5.1 Simulation, Validation, Verification and Composition

Simulation of a PN is straightforward.  Similarly, validation can be done by interactive simulation: hypothetical cases, in many cases a predefined test suite, are fed to the system to see whether they generate the expected output and the expected effects relative to the PN representation. For verification, composition and performance analysis more advanced analysis techniques are needed. Fortunately, many powerful analysis techniques have been developed for Petri Nets [5,11,26]. Linear algebraic techniques can be used to verify many properties, e.g., place invariants, transition invariants, and (non-)reachability. Coverability graph analysis, model checking, and reduction techniques can be used to analyze the dynamic behavior of a Petri Net. Simulation and Markov-chain analysis can be used for performance evaluation.

 

Three of the most important verification problems are: reachability, liveness and existence of deadlocks.  With the proliferation of embedded devices, the issue of safe operation is becoming central to device verification. In the context of Web services, verification that a composite service upholds a safety constraint (e.g., ensuring that a credit card is only debited once per transaction, or not executing the order to send the merchandise until the goods are paid for) is critical.  In what follows, we show that the verification of safety constraints, the detection of deadlock, and the automated composition of Web services can be characterized in terms of the notion of reachability.[7]

 

Definition 5 (Reachability)  A marking M is reachable if it is the marking reached by some occurrence sequence (Definition 4). Given a marking M of N, the set of reachable markings of the net (P; T; F; M) (i.e., the net obtained by replacing the initial marking M₀ by M) is denoted by [M >.

 

Notice that the empty sequence is an occurrence sequence and that it reaches the initial marking M₀. The reachability problem for a net N is the problem of deciding for a given marking M of N if it is reachable. 

 

Safety of a distributed system is defined as lack of reachabilility to an unsafe state.

 

Definition 6 (Safety of Web Service Compositions) Let S be a Web service composition with associated net (P;T;F;M).  Let f be a safety constraint, and let marking M’ encode the negation (i.e., the violation) of the safety constraint f.  Then a Web service composition S is safe with respect to f  iff there is no occurrence sequence of the net of S that reaches M’.

 

Analogously we define the task of generating a composition of Web services to achieve a goal as the problem of finding an occurrence sequence that reaches the marking depicting the user’s desired goal state.  The occurrence sequence dictates the sequence of Web services whose execution leads to the goal.  Sequential composition of atomic services to achieve a goal state can be realized using DAML-S and reachability analysis as described here.  We may automatically compose composite services using the same technique by compiling composite processes into macros following [22].

 

Definition 7 (Automated Composition of Web Services) Let A be a set of atomic Web services and let N=(P;T;F;M) be the net that depicts the behavior of all the services in A.  Further, let j represent the user’s goal, and let M’ be the marking that depicts this goal in N.  Then a1;a2,…;an is a sequential composition of atomic services that achieves user goal j iff a1;a2,…;an is an occurrence sequence in the reachability analysis of  M’ in N. Note, that the case of Web service composition is one of service input-output composition where an individual service is treated as atomic. This is in contrast to general process composition, where all possible interleavings should be considered.[8] Of course, given some agent goal, a service description and our process semantics, a smart agent with sufficient computational resources could compute optimal compositions by combining partial service executions.[9]

 

This notion of automated composition of Web services with macros is analogous to AI planning in systems such as Blackbox [19]  or Graphplan [6] where we have complete information about the initial situation [22].  In contrast, however, these planners look for plans of a bounded length, hence reducing the complexity of search as we will see below.  It is important to observe in the general case that the search space for most practical Web service compositions is very branchy (there are many services to choose from).  Fortunately, the resulting composition tends to be short.

 

In addition to the verification of safety constraints, another important analysis to perform is the determination of deadlock.  Deadlock is obviously an important property to consider in the composition of services, since one wishes to avoid compositions, which lead to reachable states where the service hangs and no further interaction is possible.

 

Definition 8 (Deadlock) A marking of a net is a deadlock if it enables no transitions. The deadlock problem for a net is the problem of deciding if any of its reachable markings is a deadlock.

 

5.2 Complexity of DAML-S Services Tasks

In this subsection, we relate the complexity of various Web service task to the expressiveness of DAML-S.

 

Theorem 1  The reachability problem for process models built on DAML-S (0.5) service descriptions is PSPACE-complete.

 

Proof Sketch (Theorem 1)  The proof relies on the results of [7] which showed P-Space completeness of  a specific subclass of Petri Nets which are 1-safe nets. Their proof was based on a  polynomial reduction from reachability for 1-safe nets to the LINEAR BOUNDED AUTOMATON ACCEPTANCE problem, which is known to be PSPACE-complete.

 

Definition 9 (1-Safe Nets)  A marking M of a net N is 1-safe if for every place p of the net M(p) £ 1. We identify a 1-safe marking M with the set of places p such that M(p) = 1. A net N is 1-safe if all its reachable markings are 1-safe.

 

Lemma 1 DAML-S 0.5 service descriptions result in 1-safe nets.

 

The proof can be found in an extended version of this paper, now at http://www.icsi.berkeley.edu/~snarayan/www11.html.

 

Proposition 1 (Complexity of Verification and Composition) From Theorem 1, we can conclude that the complexity of Web service safety verification and automated sequential composition of atomic services is P-SPACE in the general case.  Note however that in the case of safety verification, the net is simply the net of the individual composite service being verified, which will in general be extremely small.  In contrast, the net used for Web service composition is the net characterizing the behavior of all atomic Web services under consideration for composition.  It will be large, though the resulting occurrence sequence will in general be short.  These results are consistent with the complexity results for AI planning [2].  From Theorems 2 and 3 below we can draw similar conclusions about the complexity of our Web service automation tasks.

 

Theorem 2 Without the iterate constructs (iterate, repeat-until, repeat-while) the reachability problem for a DAML-S 0.5 process model is NP-Complete. 

 

The proof makes use of the following fact.

 

Proposition 2  DAML-S 0.5 without the iterate constructs results in an acyclic network.

 

Proof Sketch (Theorem 2)  For acyclic networks, there is a well known polynomial-time reduction to INTEGER LINEAR PROGRAMMING [7], because in an acyclic net N with initial marking M₀ a marking M is reachable iff the system of equations corresponding to the state equation M = M₀+C( X), where C is the incidence matrix of N, has an integer vector solution X.  (For the definitions of incidence matrix and state equation, see, for instance, [26].) Since INTEGER LINEAR PROGRAMMING is in NP [7], so is the reachability problem for DAML-S 0.5 without the iterate constructs.

 

Proposition 3 (Complexity of Restricted Verification and Composition) From Theorem 2 we can conclude that Web Service Safety Verification is NP-Complete for composite services without the iterate constructs.  Theorem 2 is not relevant to automated composition since the net used to generate the composition does not represent a single process.  Theorems 3 and 4 below define classes of composite Web services where safety verification is polynomial.

 

Theorem 3 Without the choice and iterate constructs, DAML-S 0.5 forms a sub-language with polynomial algorithms for reachability and deadlock of a DAML-S process.

 

Proof Sketch (Theorem 3) The proof makes use of the theory of conflict-free nets.

 

Definition 7 (Conflict-Free Nets) Conflict-free nets are a subclass in which conflicts are structurally ruled out.  A net N = (P; T; F; M0) is conflict-free if for every place p, if |p^·| > 1, then  p^·Í ^·p. Howell and Rosier show [18] that the reachability, liveness, and deadlock problems for 1-safe conflict-free nets are solvable in polynomial time.

 

Proposition 4 In DAML-S,  a) both iterate and choice introduce conflict constructs (iterate introduces a conflict between the repeat and finish transitions, while choice is by definition a structural conflict) and b) no other control construct introduces structural conflicts.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Theorem 4 Without the iterate and condition constructs, DAML-S forms a sublanguage with polynomial algorithms for reachability and deadlock of a DAML-S process.

 

Proof Sketch (Theorem 4) The proof makes use of the theory of  free-choice nets.

 

Definition 8 (Free-Choice Nets) A net N = (P; T; F; M₀) is free-choice if for any pair (p; t) Î F Ç (T  X P), it is the case that p^·.= {t} or ^·p = {t}. In a free-choice net, if some transitions share an input place p, then p is their unique input place. It follows that if any of them is enabled, then all of them are enabled. Therefore, it is always possible to freely choose which of them occurs. The reachability problem is still PSPACE-complete for 1-safe free-choice nets.

 

Proposition 5  In DAML-S,  a) both iterate and condition introduce nonfree constructs and b) no other control construct introduces nonfree constructs.

 

Proposition 6 DAML-S modulo the iterate and condition constructs results in a free-choice net.

 

The principal verification tractability results are shown in Table 1. We have not discussed the issue of resources in this paper.  Resources are not common with Web-accessible programs, but they are common with devices.  With resources, the DAML-S language becomes equivalent to general place transition nets, for which reachability and deadlock detection is known to be exponential in both space and time.  This result is included for completeness since the DAML-S coalition plans to introduce resources in a future release.

 

6.  IMPLEMENTATION

We have implemented a DAML-S interpreter that translates DAML-S markups to the simulation  and modeling environment KarmaSIM [27]. The KarmaSIM tool allows for interactive simulation and supports the various verification and performance analysis techniques outlined earlier. 

The DAML-S interpreter is a Java program that reads in DAML-S files and outputs a network description. The network is constructed recursively. Atomic processes are created as shown in Figure 1. For each control construct specified in the file, a template net is created as described in Section 4. The recursive procedure bottoms out when all the transitions correspond to atomic processes. The network thus constructed can then be visualized graphically using the KarmaSIM simulation environment. Once created, a variety of analysis techniques including reachability analysis, deadlock detection, invariant computations (T and S invariants) can be performed for different intial states. The service provider can also perform interactive simulations to validate various hypothetical interaction scenarios, as well as to enact the canonical usage of the service. Built into the framework are also quantitative analysis techniques that can compute throughputs, as well as most-likely paths using a variety of Markov Chain analysis techniques. A more complete description of the KarmaSIM framework can be found at http://www.ai.sri.com/daml/services/.

 

We have already used our implementation to model a variety of the existing DAML-S service ontologies. An example network, constructed from the DAML-S Congo.daml book-buying Web service, is illustrated in Figure 4 of the paper and can be found at http://www.daml.org/services/daml-s/2001/05/Congo.daml.  The thick (red) arrow indicates the stage of the interactive simulation (here the customer is ready to finish the buy transaction)[10]. The network here has a variety of non-free constructs as well as loops and exercises the full functionality of DAML-S. An earlier version of the system had a deadlock in that it does not allow a user to create a new account if there is already one known. This has since been corrected.

 

 

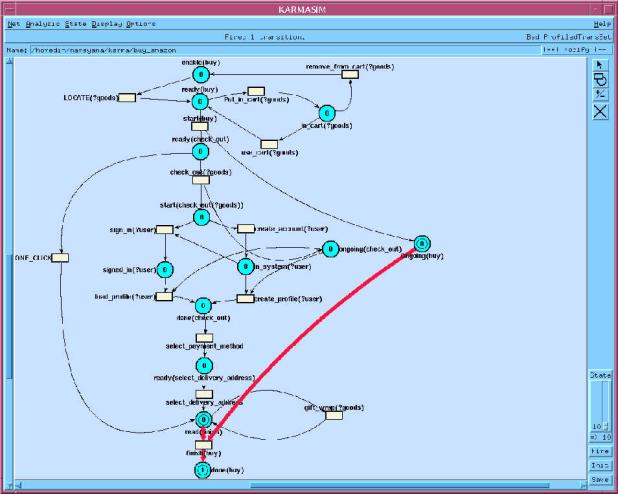
         Figure 4.  KarmaSIM simulation the DAML-S congo example

 

7.  CONCLUSION

The Semantic Web is an exciting vision for the evolution of the World Wide Web. Adding semantics enables structured information to be interpreted unambiguously. Precise interpretation is a necessary prerequisite for automatic Web search, discovery and use. Services are a particularly important component of the Semantic Web. A semantic service description language can enable a qualitative advance in the quality and quantity of e-commerce transactions on the Web [16,23]. The DAML Services Coalition, under the guise of DAML-S [9], has taken some important first steps in this direction. This paper is the first attempt to provide a model-theoretic semantics as well as a distributed operational semantics that can be used for simulation, validation, verification, automated composition and enactment of DAML-S-described Web services. The benefits of our approach include:

Formal executable semantics: a service description is fully represented using the machinery of situation calculus and its execution behavior unambiguously described using Petri Nets.

Analysis techniques and tools:  mapping DAML-S onto situation calculus and Petri Nets allows us to tap into a rich repository of analysis techniques and tools.

Service implementation tool: we mapped the DAML-S service description to an existing process model which was able to perform simulation, enactment and analysis of composite service descriptions.

Complexity and reasoning: the expressive power of the DAML-S process model compares to ordinary Petri Nets.  We identified more tractable subsets of DAML-S which trade expressiveness for more efficient analysis for verification, composition and model checking.

 

We described an implemented system that is able to read in DAML-S service descriptions and perform simulation, enactment and analysis that can a) aid the service provider to test the functional correctness and tune the performance of her service,  and b) enable service composition agents to automatically configure a sequence of atomic services to achieve a specific goal.  Furthermore, our model provides guidelines for important future  extensions to DAML-S in the direction of richer execution monitoring constructs and more expressive resource-based reasoning constructs. While this paper outlined our computational  model and implementation with respect to the DAML-S markup language, we believe that the tools and techniques described are broadly applicable and necessary for realizing the vision of a Semantic Web.

 

 

 

8.  ACKNOWLEDGEMENTS

We would like to acknowledge our colleagues in the DAML Services Coalition for development of the DAML-S ontology.  We would also like to thank the members of the DAML groups at KSL, Stanford and at SRI International for interesting discussions on various aspects of this work. We particularly thank the WWW11 anonymous reviewers for an informative and thorough review of this paper.  Finally we gratefully acknowledge the financial support of the US Defense Advanced Research Projects Agency DARPA Agent Markup Language (DAML) Program #F30602-00-C-0168 and  #F30602-00-2-0579-P00001.

 

 

9.  REFERENCES

[1] van der Aalst, W..M..P. Woflan: A Petri-net-based workflow analyzer, Systems Analysis - Modelling - Simulation, 35(3):345-357, 1999.

 

[2] Baral, C., Kreinovich, V. and Trejo, R. Computational complexity of planning and approximate planning in the presence of incompleteness, Artificial Intelligence, 122(1-2):241-267, 2000.

 

[3]  V. Richard Benjamins, Enric Plaza,Enrico Motta, Dieter Fensel, Rudi Studer, Bob Wielinga, Guus Schreiber and Zdenek Zdrahal:Benjamins, V.R., Plaza, E., Motta, E., Fensel, D., Studer, R.,  Wielinga, B., Schreiber, G.,  and Zdrahal, Z. IBROW3 - An intelligent brokering service for knowledge-component reuse on the world wide web. Proc.11^th Banff Knowledge Acquisition for Knowledge-Based System Workshop (KAW’98), 1998.

http://spuds.cpsc.ucalgary.ca/KAW/KAW98/KAW98Proc.html

 

[4] Berners-Lee, T., Hendler, J., Lassila, O. The Semantic Web, Scientific American, May, 2001.

 

[5] Best, E. and Desel, J. Partial order behaviour and structure of Petri Nets. Formal Aspects of Computing, 2:123-138, 1990.

 

[6] Blum, A.L. and Furst, M.L. Fast Planning through Planning Graph Analysis, Artificial Intelligence, 90(1-2):281-300, 1997.

 

[7] Cheng, A. and Esperza, J. Complexity results for 1-safe nets, FST&TCS 13, Foundations of Software Technology & Theoretical Computer Science, 1993.

 

[8] DAML-S versions 0.5 and 0.6. http://www.daml.org/services/.

 

[9] DAML Services Coalition: Ankolekar, A., Burstein, M., Hobbs, J., Lassila, O., Martin, D., McIlraith, S., Narayanan, S., Paolucci, M., Payne, T., Sycara, K., Zeng, H. DAML-S: Semantic Markup for Web Services, Proc. International Semantic Web Working Symposium (SWWS), 2001.

 

[10] Denker, G., Hobbs, J., Martin D., Narayanan, S. and Waldinger,  R., Querying and accessing information on the semantic web, Proc. Semantic Web Workshop, in conjunction with 10th International Worldwide Web Conference, 2001.

 

[11] Desel, J. and Esparza, J. Shortest paths in reachability graphs. Proc. Application and Theory of Petri Nets, pp. 224-241, Springer-Verlag (LNCS 691), 1993.

 

[12] Ellis, C.A. and G.J. Nutt, Modelling and enactment of workflow systems, Application and Theory of Petri Nets, LNCS 691, pp. 1-16, Springer-Verlag, 1993.

 

[13] Fikes, R. and McGuinness, D.  An Axiomatic Semantics for RDF, RDF-S, and DAML+OIL, Manuscript.  March, 2001.

 http://www.daml.org/2001/03/axiomatic-semantics.html

 

[14] De Giacomo, G., Lesperance, Y. and Levesque, H. ConGolog, a concurrent programming language based on the situation calculus. Artificial Intelligence, 121(1-2):109-169, 2000.

 

[15]  Gruninger, M.  Personal communications, August, 2001.

 

[16] Hendler, J. Agents on the Web. IEEE Intelligent Systems. Special Issue on the Semantic Web. 16(2) March/April, 2001.

 

[17] Hendler, J. and McGuinness, D. The DARPA Agent Markup Language. IEEE Intelligent Systems, Trends and Controversies, pp. 6-7, November/December 2000.

 

[18] Howell, R. and Rosier, L.E. Problems concerning fairness and temporal logic for conflict-free Petri Nets. Theoretical Computer Science, 64(3):305-329, 1989.

 

[19] H. Kautz and B. Selman, Unifying SAT-based and graph-based planning, Proc. 16^th International Joint Conference on Artificial Intelligence (IJCAI’99), 1999.

 

[20] Lowe, D. et al. BizTalk(TM) Server: The Complete Reference.  November, 2001.

 

[21] Mayr, E.W. An algorithm for the general Petri net reachability problem. SIAM Journal on Computing, 13:441-460, 1984.

 

[22] McIlraith, S. and Fadel, R.  Planning with Complex Actions. 

Proc. International Workshop  on Non-Monotonic Reasoning (NMR2002). To appear, 2002. 

 

[23] McIlraith, S. Son, T.C. and Zeng, H. Semantic Web services , IEEE Intelligent Systems. Special Issue on the Semantic Web. 16(2):46-53, March/April, 2001.

 

[24] McIlraith, S. and Son, T. Adapting Golog for composition of semantic Web services, Proc 8^th International Conference on Principles of Knowledge Representation and Reasoning. To appear, 2002.

 

[25] Meseguer, J. and Montanari, U. Petri Nets are monoids. Information and Computation, 88:105, 1990.

 

[26] Murata, T. Petri Nets: Properties, analysis and applications. Proc. of the IEEE,  77(4):541-580, 1989.

 

[27] Narayanan, S. Reasoning About Actions in Narrative Understanding. Proc. International Joint Conference on Artificial Intelligence (IJCAI '99), pp. 350-358, 1999.

 

[28] Reiter, R. Knowledge in Action:  Logical Foundations for Specifying and Implementing Dynamical Systems.  MIT Press, 2001.

 

[29] Schlenoff, M. Gruninger, F. Tissot,  J. Valois, J. Lubell, J. Lee, The Process Specification Language (PSL): Overview and Version 1.0 Specification, NISTIR 6459, National Institute of Standards and Technology, Gaithersburg, MD, 2001.

 

[30] van Harmelen, F. and Horrocks, I.  FAQs on OIL: the Ontology Inference Layer. IEEE Intelligent Systems, Trends and Controversies, pp. 3-6, November/December 2000.

 

[31] Waldinger, R. Deductive composition of Web software agents. Proc. NASA Goddard Workshop on Formal Approaches to Agent-Based Systems, LNCS 1871, Springer-Verlag. 2000.

 

[32] Winskel, G. Petri Nets, algebras, morphisms and compositionality. Information and Computation, 72(3):197-238, 1987.