Optimal Crawling Strategies for Web Search Engines

J.L. Wolf, M.S. Squillante, P.S. Yu
IBM T.J. Watson Research Center
{jlwolf,mss,psyu}@us.ibm.com

J. Sethuraman
Columbia University
jay@ieor.columbia.edu

L. Ozsen
Northwestern University
ozsen@yahoo.com

Copyright is held by the author/owner(s).
WWW2002, May 7-11, 2002, Honolulu, Hawaii, USA.
ACM 1-58113-449-5/02/0005.

Abstract

1  Introduction

Web search engines play a vital role on the World Wide Web, since they provide for many clients the first pointers to web pages of interest. Such search engines employ crawlers to build local repositories containing web pages, which they then use to build data structures useful to the search process. For example, an inverted index is created that typically consists of, for each term, a sorted list of its positions in the various web pages.

On the other hand, web pages are frequently updated by their owners [8,21,27], sometimes modestly and sometimes more significantly. A large study in [2] notes that 23% of the web pages change daily, while 40% of commercial web pages change daily. Some web pages disappear completely, and [2] reports a half-life of 10 days for web pages. The data gathered by a search engine during its crawls can thus quickly become stale, or out of date. So crawlers must regularly revisit the web pages to maintain the freshness of the search engine's data.

In this paper, we propose a two-part scheme to optimize the crawling (or perhaps, more precisely, the recrawling) process. One reasonable goal in such a scheme is the minimization of the average level of staleness over all web pages, and the scheme we propose here can solve this problem. We believe, however, that a slightly different metric provides greater utility. This involves a so-called embarrassment metric: The frequency with which a client makes a search engine query, clicks on a url returned by the search engine, and then finds that the resulting page is inconsistent with respect to the query. In this context, goodness would correspond to the search engine having a fresh copy of the web page. However, badness must be partitioned into lucky and unlucky categories: The search engine can be bad but lucky in a variety of ways. In order of increasing luckiness the possibilities are: (1) The web page might be stale, but not returned to the client as a result of the query; (2) The web page might be stale, returned to the client as a result of the query, but not clicked on by the client; and (3) The web page might be stale, returned to the client as a result of the query, clicked on by the client, but might be correct with respect to the query anyway. So the metric under discussion would only count those queries on which the search engine is actually embarrassed: The web page is stale, returned to the client, who clicks on the url only to find that the page is either inconsistent with respect to the original query, or (worse yet) has a broken link. (According to [17], and noted in [6], up to 14% of the links in search engines are broken, not a good state of affairs.)

The first component of our proposed scheme determines the optimal number of crawls for each web page over a fixed period of time called the scheduling interval, as well as determining the theoretically optimal (ideal) crawl times themselves. These two problems are highly interconnected. The same basic scheme can be used to optimize either the staleness or embarrassment metric, and is applicable for a wide variety of stochastic update processes. The ability to handle complex update processes in a general unified framework turns out to be an important advantage and a contribution of our approach in that the update patterns of some classes of web pages appear to follow fairly complex processes, as we will demonstrate. Another important model supported by our general framework is motivated by, for example, an information service that updates its web pages at certain times of the day, if an update to the page is necessary. This case, which we call quasi-deterministic, is characterized by web pages whose updates might be characterized as somewhat more deterministic, in the sense that there are fixed potential times at which updates might or might not occur. Of course, web pages with deterministic updates are a special case of the quasi-deterministic model. Furthermore, the crawling frequency problem can be solved under additional constraints which make its solution more practical in the real world: For example, one can impose minimum and maximum bounds on the number of crawls for a given web page. The latter bound is important because crawling can actually cause performance problems for web sites.

This first component problem is formulated and solved using a variety of techniques from probability theory [23,28] and the theory of resource allocation problems [12,14]. We note that the optimization problems described here must be solved for huge instances: The size of the World Wide Web is now estimated at over one billion pages, the update rate of these web pages is large, a single crawler can crawl more than a million pages per day, and search engines employ multiple crawlers. (Actually, [2] notes that their own crawler can handle 50-100 crawls per second, while others can handle several hundred crawls per second. We should note, however, that crawling is often restricted to less busy periods in the day.) A contribution of this paper is the introduction of state-of-the-art resource allocation algorithms to solve these problems.

The second component of our scheme employs as its input the output from the first component. (Again, this consists of the optimal numbers of crawls and the ideal crawl times). It then finds an optimal achievable schedule for the crawlers themselves. This is a parallel machine scheduling problem [3,20] because of the multiple crawlers. Furthermore, some of the scheduling tasks have release dates, because, for example, it is not useful to schedule a crawl task on a quasi-deterministic web page before the potential update takes place. Our solution is based on network flow theory, and can be posed specifically as a transportation problem [1]. This problem must also be solved for enormous instances, and again there are fast algorithms available at our disposal. Moreover, one can impose additional real-world constraints, such as restricted crawling times for a given web page.

We know of relatively few related papers in the research literature. Perhaps the most relevant is [6]. (See also [2] for a more general survey article.) In [6] the authors essentially introduce and solve a version of the problem of finding the optimal number of crawls per page. They employ a staleness metric and assume a Poisson update process. Their algorithm solves the resulting continuous resource allocation problem by the use of Lagrange multipliers. In [7] the authors also study a similar problem (Poisson updates, but with general crawl time distributions), with weights proportional to the page update frequencies. They present a heuristic to handle large problem instances. The problem of optimizing the number of crawlers is tackled in [26], based on a queueing-theoretic analysis, in order to avoid the two extremes of starvation and saturation. In summary, there is some literature on the first component of our crawler optimization scheme, though we have noted above several potential advantages of our approach. To our knowledge, this is the first paper that meaningfully examines the corresponding scheduling problem which is the second component of our scheme.

Another important aspect of our study concerns the statistical properties of the update patterns for web pages. This clearly is a critical issue for the analysis of the crawling problem, but unfortunately there appears to be very little in the literature on the types of update processes found in practice. To the best of our knowledge, the sole exception is a recent study [19] which suggests that the update processes for pages at a news service web site are not Poisson. Given the assumption of Poisson update processes in most previous studies, and to further investigate the prevalence of Poisson update processes in practice, we analyze the page update data from a highly accessed web site serving highly dynamic pages. A representative sample of the results from our analysis are presented and discussed. Most importantly, these results demonstrate that the interupdate processes span a wide range of complex statistical properties across different web pages and that these processes can differ significantly from a Poisson process. By supporting in our general unified approach such complex update patterns (including the quasi-deterministic model) in addition to the Poisson case, we believe that our optimal scheme can provide even greater benefits in real-world environments.

The remainder of this paper is organized as follows. Section 2 describes our formulation and solution for the twin problems of finding the optimal number of crawls and the idealized crawl times. We loosely refer to this first component as the optimal frequency problem. Section 3 contains the formulation and solution for the second component of our scheme, namely the scheduling problem. Section 4 discusses some issues of parameterizing our approach, including several empirical results on update pattern distributions for real web pages based on traces from a production web site. In Section 5 we provides experimental results showing both the quality of our solutions and their running times. Section 6 contains conclusions and areas for future work.

2  Crawling Frequency Problem

2.1  General Framework

We denote by N the total number of web pages to be crawled, which shall be indexed by i. We consider a scheduling interval of length T as a basic atomic unit of decision making, where T is sufficiently large to support our model assumptions below. The basic idea is that these scheduling intervals repeat every T units of time, and we will make decisions about one scheduling interval using both new data and the results from the previous scheduling interval. Let R denote the total number of crawls possible in a single scheduling interval.

Let u_i,n Î I R⁺ denote the point in time at which the n^th update of page i occurs, where 0 < u_i,1 < u_i,2 < ¼ £ T, i Î { 1, 2, ¼, N }. Associated with the n^th update of page i is a mark k_i,n Î I K, where k_i,n is used to represent all important and useful information for the n^th update of page i and I K is the space of all such marks (called the mark space). Examples of possible marks include information on the probability of whether an update actually occurs at the corresponding point in time (e.g., see Section 2.3.3) and the probability of whether an actual update matters from the perspective of the crawling frequency problem (e.g., a minimal update of the page may not change the results of the search engine mechanisms). The occurrences of updates to page i are then modeled as a stationary stochastic marked point process U_i = { (u_i,n , k_i,n)  ;  n Î I N } defined on the state space I R⁺ × I K. In other words, U_i is a stochastic sequence of points { u_i,1, u_i,2, ¼} in time at which updates of page i occur, together with a corresponding sequence of general marks { k_i,1, k_i,2, ¼} containing information about these updates.

A counting process N_i^u(t) is associated with the marked point process U_i and is given by N_i^u(t) º max{ n : u_i,n £ t }, t Î I R₊. This counting process represents the number of updates of page i that occur in the time interval [0,t]. The interval of time between the n-1^st and n^th update of page i is given by U_i,n º u_i,n - u_i,n-1, n Î I N, where we define u_i,0 º 0 and k_i,0 º Æ. The corresponding forward and backward recurrence times are given by A_i^u(t) º u_i,Ni^u(t)+1 - t and B_i^u(t) º t - u_i,Ni^u(t), respectively, t Î I R₊. In this paper we shall make the assumption that the time intervals U_i,n Î I R⁺ between updates of page i are independent and identically distributed (i.i.d.) following an arbitrary distribution function G_i (·) with mean l_i^-1 > 0, and thus the counting process N_i^u(t) is a renewal process [23,28], i Î { 1, 2, ¼, N }. Note that u_i,0 does not represent the time of an actual update, and therefore the counting process { N_i^u(t)  ;  t Î I R₊ } (starting at time 0) is, more precisely, an equilibrium renewal process (which is an instance of a delayed renewal process) [23,28].

Suppose we decide to crawl web page i a total of x_i times during the scheduling interval [0,T] (where x_i is a non-negative integer less than or equal to R), and suppose we decide to do so at the arbitrary times 0 £ t_i,1 < t_i,2 < ¼ < t_i,xi £ T. Our approach in this paper is based on computing a particular probability function that captures, in a certain sense, whether the search engine will have a stale copy of web page i at an arbitrary time t in the interval [ 0 , T]. From this we can in turn compute a corresponding time-average staleness estimate a_i (t_i,1, ¼, t_i,xi) by averaging this probability function over all t within [ 0 , T]. Specifically, we consider the arbitrary time t_i,j as falling within the interval U_{i,Ni^u(ti,j)+1} between the two updates of page i at times u_i,Ni^u(ti,j) and u_{i,Ni^u(ti,j)+1}, and our interest is in a particular time-average measure of staleness with respect to the forward recurrence time A_i^u(t_i,j) until the next update, given the backward recurrence time B_i^u(t_i,j). Figure 1 depicts a simple example of this situation.

Figure 1: Example of Stationary MPP Framework

More formally, we exploit conditional probabilities to define the following time-average staleness estimate

ai (ti,1, ¼, ti,xi) =  1 T    xi å j=0     ó õ ti,j+1 ti,j  æ è ó õ ¥ 0    \sf P[  A,B,C  ] \sf P[  B  ]  gBiu(v)  dv   ö ø  dt ,      (1)

where A = { U_i,ni,j+1 £ t - t_i,j + v }, B = { U_i,ni,j+1 > v }, C = { k_i,ni,j+1 Î K }, t_i,0 º 0, t_i,xi+1 º T, n_i,j º N_i^u(t_i,j), g_Bi^u(·) is the stationary density for the backward recurrence time, and K Ì I K is the mark set of interest for the staleness estimate under consideration. Note that the variable v is used to integrate over all possible values of B_i^u(t_i,j) Î [0,¥). Further observe the dependence of the staleness estimate on the update patterns for web page i.

When K = I K (i.e., all marks are considered in the definition of the time-average staleness estimate), then the inner integral above reduces as follows:

ó õ ¥ 0    Gi( t - ti,j + v ) - Gi( v ) 1 - Gi( v ) gBiu(v) dv = ó õ ¥ 0  æ ç ç è 1 - G   i  ( t - ti,j + v ) G   i  ( v ) ö ÷ ÷ ø gBiu(v) dv ;      (2)

where [`G]<sub>i</sub>(t) º 1 - G<sub>i</sub>(t) is the tail distribution of the interupdate times U<sub>i,n</sub>, n Î I N. From standard renewal theory [23,28], we have g<sub>Bi<sup>u</sup></sub>(t) = l<sub>i</sub>[`G]_i(t), and thus after some simple algebraic manipulations we obtain

ai (ti,1, ¼, ti,xi) =  1 T xi å j=0  ó õ ti,j+1 ti,j  æ è  1  -  li ó õ ¥ 0  G   i  ( t - ti,j + v )  dv   ö ø  dt.          (3)

Naturally we would also like the times t_i,1, ¼t_i,xi to be chosen so as to minimize the time-average staleness estimate a_i (t_i,1, ¼, t_i,xi), given that there are x_i crawls of page i. Deferring for the moment the question of how to find these optimal values t_i,1^*, ¼t_i,xi^*, let us define the function A_i by setting

Ai (xi) = ai (ti,1*, ¼, ti,xi*) .

(4)

Thus, the domain of this function A_i is the set {0, ¼, R }.

We now must decide how to find the optimal values of the x_i variables. While one would like to choose x_i as large as possible, there is competition for crawls from the other web pages. Taking all web pages into account, we therefore wish to minimize the objective function

N å i=1  wi Ai ( xi )

(5)

subject to the constraints

N å i=1  xi = R, (6) xi Î { 0, ¼,R }.          (7)

Here the weights w_i will determine the relative importance of each web page i. If each weight w_i is chosen to be 1, then the problem becomes one of minimizing the time-average staleness estimate across all the web pages i. However, we will shortly discuss a way to pick these weights a bit more intelligently, thereby minimizing a metric that computes the level of embarrassment the search engine has to endure.

The optimization problem just posed has a very nice form. Specifically, it is an example of a so-called discrete, separable resource allocation problem. The problem is separable by the nature of the objective function, written as the summation of functions of the individual x_i variables. The problem is discrete because of the second constraint, and a resource allocation problem because of the first constraint. For details on resource allocation problems, we refer the interested reader to [12]. This is a well-studied area in optimization theory, and we shall borrow liberally from that literature. In doing so, we first point out that there exists a dynamic programming algorithm for solving such problems, which has computational complexity O(NR²).

Fortunately, we will show shortly that the function A_i is convex, which in this discrete context means that the first differences A_i (j+1) - A_i (j) are non-decreasing as a function of j. (These first differences are just the discrete analogues of derivatives.) This extra structure makes it possible to employ even faster algorithms, but before we can do so there remain a few important issues. Each of these issues is discussed in detail in the next three subsections, which involve: (1) computing the weights w_i of the embarrassment level metric for each web page i; (2) computing the functional forms of a_i and A_i for each web page i, based on the corresponding marked point process U_i; and (3) solving the resulting discrete, convex, separable resource allocation problem in a highly efficient manner.

It is important to point out that we can actually handle a more general resource allocation constraint than that given in Equation (7). Specifically, we can handle both minimum and maximum number of crawls m_i and M_i for each page i, so that the constraint instead becomes x_i Î { m_i, ¼,M_i } . We can also handle other types of constraints on the crawls that tend to arise in practice [4], but omit details here in the interest of space.

2.2  Computing the Weights w_i

Consider Figure 2, which illustrates a decision tree tracing the possible results for a client making a search engine query. Let us fix a particular web page i in mind, and follow the decision tree down from the root to the leaves.

Figure 2: Embarrassment Level Decision Tree

The first possibility is for the page to be fresh: In this case the web page will not cause embarrassment to the search engine. So, assume the page is stale. If the page is never returned by the search engine, there again can be no embarrassment: The search engine is simply lucky in this case. What happens if the page is returned? A search engine will typically organize its query responses into multiple result pages, and each of these result pages will contain the urls of several returned web pages, in various positions on the page. Let P denote the number of positions on a returned page (which is typically on the order of 10). Note that the position of a returned web page on a result page reflects the ordered estimate of the search engine for the web page matching what the user wants. Let b_i,j,k denote the probability that the search engine will return page i in position j of query result page k. The search engine can easily estimate these probabilities, either by monitoring all query results or by sampling them for the client queries.

The search engine can still be lucky even if the web page i is stale and returned: A client might not click on the page, and thus never have a chance to learn that the page was stale. Let c_j,k denote the frequency that a client will click on a returned page in position j of query result page k. These frequencies also can be easily estimated, again either by monitoring or sampling.

One can speculate that this clicking probability function might typically decrease both as a function of the overall position (k-1) P +j of the returned page and as a function of the page k on which it is returned. Assuming a Zipf-like function [29,15] for the first function and a geometric function to model the probability of cycling through k-1 pages to get to returned page k, one would obtain a clicking probability function that looks like the one provided in Figure 3. (According to  [4] there is some evidence that the clicking probabilities in Figure 3 actually rise rather than fall as a new page is reached. This is because some clients do not scroll down - some do not even know how to do so. More importantly,  [4] notes that this data can actually be collected by the search engine.)

Figure 3: Probability of Clicking as Function of Position/Page

Finally, even if the web page is stale, returned by the search engine, and clicked on: The changes to the page might not cause the results of the query to be wrong. This truly lucky loser scenario can be more common than one might initially suspect, because most web pages typically do not change in terms of their basic content, and most client queries will probably try to address this basic content. In any case, let d_i denote the probability that a query to a stale version of page i yields an incorrect response. Once again, this parameter can be easily estimated.

Assuming, as seems reasonable, that these three types of events are independent, one can compute the total level of embarrassment caused to the search engine by web page i as

wi = di å j  å k  cj,k bi,j,k.

(8)

Note that although the functional form of the above equation is a bit involved, the value of w_i is simply a constant from the perspective of the resource allocation problem.

2.3  Computing the Functions a_i and A_i

2.3.1  Exponential Distribution Function G_i

Suppose as before that we crawl a total of x_i times in the scheduling interval at the arbitrary times t_i,1, ¼t_i,xi. It then follows from Equation (3) that the time-average staleness estimate is given by

ai (ti,1, ¼, ti,xi) =  1 T xi å j=0  ó õ ti,j+1 ti,j  æ è 1  -  li ó õ ¥ 0  e-li (t - ti,j + v)  dv   ö ø  dt =  1 T xi å j=0  ó õ ti,j+1 ti,j  ( 1  -  e-li (t - ti,j) )  dt . (9)

After some minor algebraic manipulations, we obtain that the time-average staleness estimate is given by

ai (ti,1, ¼, ti,xi) = 1 +  1 li T xi å j=0  ( e- li (ti,j+1-ti,j ) - 1 ) . (10)

Letting T_i,j = t_i,j+1 - t_i,j for all 0 £ j £ x_i, then the problem of finding A_i reduces to minimizing

1 +  1 li T xi å j=0  ( e- li Ti,j - 1 )

(11)

subject to the constraints

0 £ Ti,j £ T, (12) xi å j=0  Ti,j = T. (13)

Modulo a few constants, which are not important to the optimization problem, this now takes the form of a continuous, convex, separable resource allocation problem. As before, the problem is separable by the nature of the objective function. It is continuous because of the first constraint, and it is a resource allocation problem because of the second constraint; it is also convex for the reasons provided below.

The key point is that the optimum value is known to occur at the value (T_i,1^*, ¼, T_i,xi^*) where the derivatives T^-1 e^{-l_i T_i,j*} of the summands in Equation (11) are equal, subject to the constraints 0 £ T_i,j^* £ T and å_j=0^x_i T_i,j^* = T. The general result, originally due to [9], was the seminal paper in the theory of resource allocation problems, and there exist several fast algorithms for finding the values of T_i,j^*. See [12] for a good exposition of these algorithms. In our special case of the exponential distribution, however, the summands are all identical, and thus the optimal decision variables as well can be found by inspection: They occur when each T_i,j^*=T/(x_i + 1). Hence, we can write

Ai (xi) = 1 +  xi +1 li T ( e- li T/(xi +1) - 1 ),

(14)

which is easily shown to be convex.

2.3.2  General Distribution Function G_i

2.3.3  Quasi-Deterministic Case

A key observation is that all crawls should be done at the potential update times, because there is no reason to delay beyond when the update has occurred. This also implies that we can assume x_i £ Q_i +1, as there is no reason to crawl more frequently. (The maximum of Q_i+1 crawls corresponds to the time 0 and the Q_i other potential update times.) Hence, consider the binary decision variables

yi,j = ì í î 1 , if a crawl occurs at time ui,j ; 0 , otherwise .

(15)

If we crawl x_i times, then we have å_j=0^Q_i y_i,j = x_i.

Note that, as a consequence of the above assumptions and observations, the two integrals in Equation (1) reduce to a much simpler form. Specifically, let us consider a staleness probability function [`p] (y_i,0, ¼, y_i,Qi, t) at an arbitrary time t, which we now compute. Recall that N_i^u(t) provides the index of the latest potential update time that occurs at or before time t, so that N_i^u(t) £ Q_i. Similarly, define

Ji(t)      =      max { j : ui,j £ t ,   yi,j=1 ,    0 £ j £ Qi }+ ,

(16)

which is the index of the latest potential update time at or before time t that is actually going to be crawled. Clearly we can also unambiguously use J_i,j to abbreviate the value of J_i(t) at any time t for which j=N_i^u(t). Now we have

- p   (yi,0, ¼, yi,Qi, t)      =      1 - Niu(t) Õ j=Ji(t)+1  (1- ki,j),

(17)

where a product over the empty set, as per normal convention, is assumed to be 1.

Figure 4 illustrates a typical staleness probability function [`p]. (For visual clarity we display the freshness function 1-[`p] rather than the staleness function in this figure.) Here the potential update times are noted by circles on the x-axis. Those which are actually crawled are depicted as filled circles, while those that are not crawled are left unfilled. The freshness function jumps to 1 during each interval immediately to the right of a crawl time, and then decreases, interval by interval, as more terms are multiplied into the product (see Equation (17)). The function is constant during each interval - that is precisely why J_i,j can be defined.

Figure 4: Freshness Probability Function for Quasi-Deterministic Web Pages

Now we can compute the corresponding time-average probability estimate as

- a   (yi,0, ¼, yi,Qi) = Qi å j=0  ui,j[1- j Õ k=Ji,j+1  (1- ki,j)].

(18)

The question of how to choose the optimal x_i crawl times is perhaps the most subtle issue in this paper. We can write this as a discrete resource allocation problem, namely the minimization of Equation (18) subject to the constraints y_i,j Î {0, 1 } and å_j=0^Q_i y_i,j = x_i. The problem with this is that the decision variables y_i,j are highly intertwined in the objective function. While our optimization problem can be solved exactly by the use of so-called non-serial dynamic programming algorithms, as shown in [12], or can be solved as a general integer program, such means to obtain the problem solution will not have good performance. Hence, for reasons we shall describe momentarily, we choose to employ a greedy algorithm for the optimization problem: That is, we first estimate the value of A_i (1) by picking that index 0 £ j £ Q_i for which the objective function will decrease the most when y_i,j is turned from 0 to 1. In the general inductive step we assume that we are given an estimate for A_i (x_i -1). Then to compute A_i (x_i ) we pick that index 0 £ j £ Q_i with y_i,j=0 for which the objective function decreases the most upon setting y_i,j=1. It can be shown that the greedy algorithm does not, in general, find the optimal solution. However, the average freshness can be easily shown to be an increasing, submodular function (in the number of crawls), and so the greedy algorithm is guaranteed to produce a solution with average freshness at least (1 - 1/e) of the best possible [18]. For the special case we consider, we believe the worst-case performance guarantee of the greedy algorithm is strictly better. We therefore feel justified in suggesting the greedy algorithm as a heuristic to find A_i in general. Moreover, it is trivial to check that the function A_i, when estimated in this way, is convex: If, given two successive greedy choices, the first difference decreases, then the second greedy choice would have been chosen before the first one.

2.4  Solving the Discrete Separable Convex
Resource Allocation Problem

N å i=1  Fi ( xi )

(19)

subject to the constraints

N å i=1  xi = R

(20)

and

xi Î { mi, ¼,Mi }

(21)

with convex F_is is very well studied in the optimization literature. We point the reader to [12] for details on these algorithms. We content ourselves here with a brief overview.

The earliest known algorithm for discrete, convex, separable resource allocation problems is essentially due to Fox [9]. More precisely, Fox looked at the continuous case, noting that the Lagrange multipliers (or Kuhn-Tucker conditions) implied that the optimal value occurred when the derivatives were as equal as possible, subject to the above constraints. This gave rise to a greedy algorithm for the discrete case which is usually attributed to Fox. One forms a matrix in which the (i,j)th term D_i,j is defined to be the first difference: D_i,j = F_i (j+1) - F_i (j). By convexity the columns of this matrix are guaranteed to be monotone, and specifically non-decreasing. The greedy algorithm initially sets each x_i to be m_i. It then finds the index i for which x_i + 1 £ M_i and the value of the next first difference D_i,xi is minimal. For this index i^* one increments x_i^* by 1. Then this process repeats until Equation (20) is satisfied, or until the set of allowable indices i empties. (In that case there is no feasible solution.) Note that the first differences are just the discrete analogs of derivatives for the continuous case, and that the greedy algorithm finds a solution in which, modulo Constraint (21), all first differences are as equal as possible. The complexity of the greedy algorithm is O(N+R logN).

There is a faster algorithm for our problem, due to Galil and Megiddo [11], which has complexity O(N (logR)² ). The fastest algorithm is due to Frederickson and Johnson [10], and it has complexity O(max{ N, N log(R/N) }). The algorithm is highly complex, consisting of three components. The first component eliminates elements of the D matrix from consideration, leaving O(R) elements and taking O(N) time. The second component iterates O(log(R/N)) times, each iteration taking O(N) time. At the end of this component only O(N) elements of the D matrix remain. Finally, the third component is a linear time selection algorithm, finding the optimal value in O(N) time. For full details on this algorithm see [12]. We employ the Frederickson and Johnson algorithm in this paper.

There do exist some alternative algorithms which could be considered for our particular optimization problem. For example, the quasi-deterministic web page portion of the optimization problem is inherently discrete, but the portions corresponding to other distributions can be considered as giving rise to a continuous problem (which is done in [6]). In the case of distributions for which the expression for A_i is differentiable, and for which the derivative has a closed form expression, there do exist very fast algorithms for (a) solving the continuous case, and (b) relaxing the continuous solution to a discrete solution. So, if all web pages had such distributions the above approach could be attractive. Indeed, if most web pages had such distributions, one could partition the set of web pages into two components. The first set could be solved by continuous relaxation, while the complementary set could be solved by a discrete algorithm such as that given by [10]. As the amount of resource given to one set goes up, the amount given to the other set would go down. So a bracket and bisection algorithm [22], which is logarithmic in complexity, could be quite fast. We shall not pursue this idea further here.

3  Crawler Scheduling Problem

We know from the previous section the desired number of crawls x_i^* for each web page i. Since we have already computed the optimal schedule for the last scheduling interval, we further know the start time t_i,0 of the final crawl for web page i within the last scheduling interval. Thus we can compute the optimal crawl times t_i,1^* , ..., t_i,xi^* for web page i during the current scheduling interval. For the stochastic case it is important for the scheduler to initiate each of these crawl tasks at approximately the proper time, but being a bit early or a bit late should have no serious impact for most of the update probability distribution functions we envision. Thus it is reasonable to assume a scheduler cost function for the jth crawl of page i, whose update patterns follow a stochastic process, that takes the form S(t) = | t - t_i,j^* |. On the other hand, for a web page i whose update patterns follow a quasi-deterministic process, being a bit late is acceptable, but being early is not useful. So an appropriate scheduler cost function for the jth crawl of a quasi-deterministic page i might have the form

S(t) = ì í î ¥ if t < ti,j* t - ti,j otherwise

(22)

In terms of scheduling notation, the above crawl task is said to have a release time of t_i,j. See [3] for more information on scheduling theory.

Virtually no work seems to have been done on the scheduling problem in the research literature on crawlers. Yet there is a simple, exact solution for the problem. Specifically, the problem can be posed and solved as a transportation problem as we shall we now describe. See [1] for more information on transportation problems and network flows in general. We describe our scheduling problem in terms of a network.

We define a bipartite network with one directed arc from each supply node to each demand node. The R supply nodes, indexed by j, correspond to the crawls to be scheduled. Each of these nodes has a supply of 1 unit. There will be one demand node per time slot and crawler pair, each of which has a demand of 1 unit. We index these by 1 £ l £ S_k and 1 £ k £ C. The cost of arc jkl emanating from a supply node j to a demand node kl is S_j (T_kl). Figure 5 shows the underlying network for an example of this particular transportation problem. Here for simplicity we assume that the crawlers are homogeneous, and thus that each can crawl the same number S=S_k of pages in the scheduling interval T. In the figure the number of crawls is R=4, which equals the number of crawler time slots. The number of crawlers is C=2, and the number of crawls per crawler is S=2. Hence R=CS.

Figure 5: Transportation Problem Network

The specific linear optimization problem solved by the transportation problem can be formulated as follows.

Minimize M å i=1  N å j=1  M å k=1  Ri (Tjk) fijk (23)

The solution of a transportation problem can be accomplished quickly. See, for example, [1].

Although not obvious at first glance, the nature of the transportation problem formulation ensures that there exists an optimal solution with integral flows, and the techniques in the literature find such a solution. Again, see [1] for details. This implies that each f_ijk is binary. If f_ijk=1 then a crawl of web page i is assigned to the jth crawl of crawler k.

If it is required to fix or restrict certain crawl tasks from certain crawler slots, this can be easily done: One simply changes the costs of the restricted directed arcs to be infinite. (Fixing a crawl task to a subset of crawler slots is the same as restricting it from the complementary crawler slots.)

4  Parameterization Issues

Note that when each page i is crawled we can easily obtain the last update time for the page. While this does not provide information about any other updates occurring since the last crawl of page i, we can use this information together with the data and models for page i from previous scheduling intervals to statistically infer key properties of the update process for the page. This is then used in turn to construct a probability distribution (including a quasi-deterministic distribution) for the interupdate times of page i.

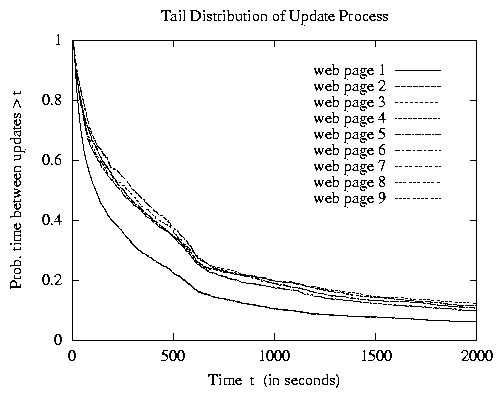
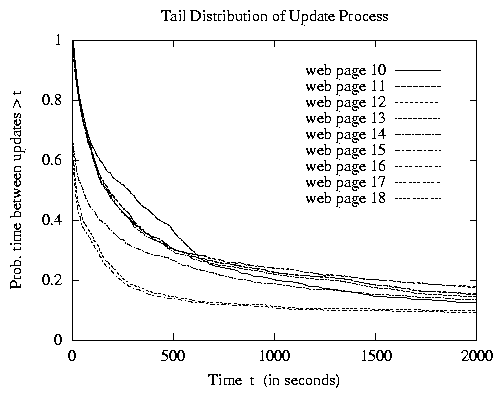
Another important aspect of our approach concerns the statistical properties of the update process. The analysis of previous studies has essentially assumed that the update process is Poisson [6,7,26], i.e., the interupdate times for each page follow an exponential distribution. Unfortunately, very little has been published in the research literature on the properties of update processes found in practice, with the sole exception (to our knowledge) of a recent study [19] suggesting that the interupdate times of pages at a news service web site are not exponential. To further investigate the prevalence of exponential interupdate times in practice, we analyze the page update data from another web site environment whose content is highly accessed and highly dynamic. Specifically, we consider the update patterns found at the web site for the 1998 Nagano Olympic Games, referring the interested reader to [16,25] for more details on this environment. Figure 6 plots the tail distributions of the time between updates for each of a set of 18 individual dynamic pages which are representative of the update pattern behaviors found in our study of all dynamic pages that were modified a fair amount of time. In other words, the curves illustrate the probability that the time between updates to a given page is greater than t as a function of time t.

We first observe from these results that the interupdate time distributions can differ significantly from an exponential distribution. More precisely, our results suggest that the interupdate time distribution for some of the web pages at Nagano have a tail that decays at a subexponential rate and can be closely approximated by a subset of the Weibull distributions; i.e., the tail of the long-tailed Weibull interupdate distribution is given by [`G](t) = e<sup>-lta</sup>, where t ³ 0, l > 0 and 0 < a < 1. We further find that the interupdate time distribution for some of the other web pages at Nagano have a heavy tail and can be closely approximated by the class of Pareto distributions; i.e., the tail of the Pareto interupdate time distribution is given by [`G](t) = ( b/ (b+ t) )^a, where t ³ 0, b > 0 and 0 < a < 2. Moreover, some of the periodic behavior observed in the update patterns for some web pages can be addressed with our quasi-deterministic distribution.

The above analysis is not intended to be an exhaustive study by any means. Our results, together with those in [19], suggest that there are important web site environments in which the interupdate times do not follow an exponential distribution. This includes the quasi-deterministic instance of our general model, which is motivated by information services as discussed above. The key point is that there clearly are web environments in which the update process for individual web pages can be much more complex than a Poisson process, and our general formulation and solution of the crawler scheduling problem makes it possible for us to handle such a wide range of web environments within this unified framework.

5  Experimental Results

In our experiments we consider combinations of different types of web page update distributions. In a number of cases we use a mixture of 60% Poisson, 30% Pareto and 10% quasi-deterministic distributions. In the experiments we choose T to be one day, though we have made runs for a week as well. We set N to be one million web pages, and varied R between 1.5 and 5 million crawls. We assumed that the average rate of updates over all pages was 1.5, and these updates were chosen according to a Zipf-like distribution with parameters N and q, the latter chosen between 0 and 1 [29,15]. Such distributions run the spectrum from highly skewed (when q = 0) to totally uniform (when q = 1). We considered both the staleness and embarrassment metrics. When considering the embarrassment metric we derived the weights in Equation (8) by considering a search engine which returned 5 result pages per query, with 10 urls on a page. The probabilities b_i,j,k with which the search engine returns page i in position j of query result page k were chosen by linearizing these 50 positions, picking a randomly chosen center, and imposing a truncated normal distribution about that center. The clicking frequencies c_j,k for position j of query page k are chosen as described in Section 2.2, via a Zipf-like function with parameters 50 and q = 0, with a geometric function for cycling through the pages. We assumed that the client went from one result page to the next with probability 0.8. We choose the lucky loser probability d_i of web page i yielding an incorrect response to the client query by picking a uniform random number between 0 and 1. All curves in our experiments display the analytically computed objective function values of the various schemes.

Figure 7 shows two experiments using the embarrassment metric. In the left-hand side of the figure we consider the results under different mixtures of update distributions by varying the ratio of R to N from 1.5 to 5. We consider here a true Zipf distribution for the update frequencies - in other words we choose Zipf-like parameter q = 0. There are six curves, namely optimal, proportional and uniform in both weighted and unweighted versions. (The unweighted optimal curve is the result of employing unit weights during the computation phase, but displaying the weighted optimal objective function.) By definition the unweighted optimal scheme will not perform as well as the weighted optimal scheme, which is indeed the best possible solution. In all other cases, however, the unweighted variant does better than the weighted variant. So the true uniform policy does the best amongst all of the heuristics, at least for the experiments considered in our study. This somewhat surprising state of affairs was noticed in [6] as well. Both uniform policies do better than their proportional counterparts. Notice that the weighted optimal curve is, in fact, convex as a function of increasing R. This will always be true.

In the right-hand side of Figure 7 we show a somewhat differing mixture of distributions. In this case we vary the Zipf-like parameter q while holding the value of R to be 2.5 million (so that R/N = 2.5). As q increases, thus yielding less skew, the objective functions generally increase as well. This is appealing, because it shows in particular that the optimal scheme does very well in highly skewed scenarios, which we believe are more representative of real web environments. Moreover, notice that the curves essentially converge to each other as q increases. This is not too surprising, since the optimal, proportional and uniform schemes would all result in the same solutions precisely in the absence of weights when q = 1. In general the uniform scheme does relatively better in this figure than it did in the previous one. The explanation is complex, but it essentially has to do with the correlation of the weights and the update frequencies. In fact, we show this example because it puts uniform in its best possible light.

In Figure 8 we show four experiments where we varied the ratio of R to N. These figures depict the average staleness metric, and so we only have three (unweighted) curves per figure. The top left-hand figure depict a mixture of update distribution types, and the other three figures depict, in turn, pure Poisson, Pareto and quasi-deterministic distributions. Notice that these curves are cleaner than those in Figure 7. The weightings, while important, introduce a degree of noise into the objective function values. For this reason we will focus on the non-weighted case from here on. The y-axis ranges differ on each of the four figures, but in all cases the optimal scheme yields a convex function of R/N (and thus of R). The uniform scheme performs better than the proportional scheme once again. It does relatively less well in the Poisson update scenario. In the quasi-deterministic figure the optimal scheme is actually able to reduce average staleness to 0 for sufficiently large R values.

In Figure 9 we explore the case of Pareto interupdate distributions in more detail. Once again, the average staleness metric is plotted as a function of the parameter a in the Pareto distribution; refer to Section 4. This distribution is said to have a heavy tail when 0 < a < 2, which is quite interesting because it is over this range of parameter values that the optimal solution is most sensitive. In particular, we observe that the optimal solution value is rather flat for values of a ranging from 4 toward 2. However, as a approaches 2, the optimal average staleness value starts to rise which continues to increase in an exponential manner as a ranges from 2 toward 0. These trends appear to hold for all three schemes, with our optimal scheme continuing to provide the best performance and uniform continuing to outperform the proportional scheme. Our results suggest the importance of supporting heavy-tailed distributions when they exist in practice (and our results of the previous section demonstrate that they do indeed exist in practice). This is appealing because it shows in particular that the optimal scheme does very well in these complex environments which may be more representative of real web environments than those considered in previous studies.

Figure 9: Pareto Example

Figure 10: Transportation Problem Example

The transportation problem solution to the scheduling problem is optimal, of course. Furthermore, the quality of the solution, measured in terms of the deviation of the actual time slots for the various tasks from their ideal time slots, will nearly always be outstanding. Figure 10 shows an illustrative example. This example involves the scheduling of one day with C=10 homogeneous crawlers and 1 million crawls per crawler. So there are 10 million crawls in all. Virtually all crawls occur within a window of plus or minus 20 time slots. We also highlight the quasi-deterministic tasks, to notice that they occur on or after their ideal time slots, as required. The quasi-deterministic crawls amounted to 20% of the overall crawls in this example. The bottom line is that this scheduling problem will nearly always yield optimal solutions of very high absolute quality.

The crawling frequency scheme was implemented in C and run on an IBM RS/6000 Model 50. In no case did the algorithm require more than a minute of elapsed time. The crawler scheduling algorithm was implemented using IBM's Optimization Subroutine Library (OSL) package [13], which can solve network flow problems. Problems of our size run in approximately two minutes.

6  Conclusion

Acknowledgement. We thank Allen Downey for pointing us to [19].

References