Topic-Sensitive PageRank
Taher H. Haveliwala1
Stanford University
Computer Science Department
Stanford, CA 94305
taherh@cs.stanford.edu
(650) 723-9273
Copyright is held by the author/owner(s).
WWW2002, May 7-11, 2002, Honolulu, Hawaii, USA.
ACM 1-58113-449-5/02/0005.
Abstract:
In the original PageRank algorithm for
improving the ranking of search-query results, a single PageRank
vector is computed, using the link structure of the Web, to capture
the relative ``importance'' of Web pages, independent of any
particular search query. To yield more accurate search results, we
propose computing a set of PageRank vectors, biased using
a set of representative topics, to capture more accurately the
notion of importance with respect to a particular topic. By using
these (precomputed) biased PageRank vectors to generate
query-specific importance scores for pages at query time, we show
that we can generate more accurate rankings than with a single,
generic PageRank vector. For ordinary keyword search queries, we
compute the topic-sensitive PageRank scores for pages satisfying
the query using the topic of the query keywords. For searches done
in context (e.g., when the search query is performed by
highlighting words in a Web page), we compute the topic-sensitive
PageRank scores using the topic of the context in which the query
appeared.
Categories and Subject Descriptors
H.3.3 [Information Storage and Retrieval]: Information Search and
Retrieval - search process, information filtering, retrieval models;
H.3.1 [Information Storage and Retrieval]: Content Analysis and
Indexing - linguistic processing
General Terms
Algorithms, Experimentation
Keywords
search, Web graph, link structure, PageRank,
search in context, personalized search
1 Introduction
Various link-based ranking strategies have been developed
recently for improving Web-search query results. The HITS algorithm
proposed in [14] relies
on query-time processing to deduce the hubs and
authorities that exist in a subgraph of the Web consisting
of both the results to a query and the local neighborhood of these
results. [4] augments the
HITS algorithm with content analysis to improve precision for the
task of retrieving documents related to a query topic (as opposed
to retrieving documents that exactly satisfy the user's information
need). [8] makes use of HITS for
automatically compiling resource lists for general topics.
The PageRank algorithm discussed in [7,16] precomputes a rank vector that
provides a-priori ``importance'' estimates for all of the pages on
the Web. This vector is computed once, offline, and is independent
of the search query. At query time, these importance scores are
used in conjunction with query-specific IR scores to rank the query
results. PageRank has a clear efficiency advantage over the HITS
algorithm, as the query-time cost of incorporating the
precomputed PageRank importance score for a page is low.
Furthermore, as PageRank is generated using the entire Web graph,
rather than a small subset, it is less susceptible to localized
link spam.
In this paper, we propose an approach that (as with HITS) allows
the query to influence the link-based score, yet (as with PageRank)
requires minimal query-time processing. In our model, we compute
offline a set of PageRank vectors, each
biased with a different topic, to create for each page a set of importance scores with respect to
particular topics. The idea of biasing the PageRank computation was
suggested in [6] for the
purpose of personalization, but was never fully explored.
This biasing process involves introducing artificial links into the
Web graph during the offline rank computation, and is described
further in Section 2.
By making PageRank topic-sensitive, we avoid the problem of
heavily linked pages getting highly ranked for queries for which
they have no particular authority [3]. Pages considered important in
some subject domains may not be considered important in others,
regardless of what keywords may appear either in the page or in
anchor text referring to the page [5]. An approach termed
Hilltop, with motivations similar to ours, is suggested
in [5] that is designed to
improve results for popular queries. Hilltop generates a
query-specific authority score by detecting and indexing pages that
appear to be good experts for certain keywords, based on their
outlinks. However, query terms for which experts were not found
will not be handled by the Hilltop algorithm.
[17] proposes using the set of Web pages
that contain some term as a bias set for influencing the PageRank
computation, with the goal of returning terms for which a
given page has a high reputation. An approach for enhancing
rankings by generating a PageRank vector for each possible query term
was recently proposed in [18] with
favorable results. However, the approach requires considerable
processing time and storage, and is not easily extended to make use of
user and query context. Our approach
to biasing the PageRank computation is novel in its use of a small number
of representative basis topics, taken from the Open Directory, in
conjunction with a unigram language model used to classify the query
and query context.
In our work we consider two scenarios. In the first, we assume a
user with a specific information need issues a query to our search
engine in the conventional way, by entering a query into a search
box. In this scenario, we determine the topics most closely
associated with the query, and use the appropriate topic-sensitive
PageRank vectors for ranking the documents satisfying the query.
This ensures that the ``importance'' scores reflect a preference
for the link structure of pages that have some bearing on the
query. As with ordinary PageRank, the topic-sensitive PageRank
score can be used as part of a scoring function that takes into
account other IR-based scores. In the second scenario, we assume
the user is viewing a document (for instance, browsing the Web or
reading email), and selects a term from the document for which he
would like more information. This notion of search in
context is discussed in [10]. For instance, if a query for
``architecture'' is performed by highlighting a term in a document
discussing famous building architects, we would like the result to
be different than if the query ``architecture'' is performed by
highlighting a term in a document on CPU design. By selecting the
appropriate topic-sensitive PageRank vectors based on the context
of the query, we hope to provide more accurate search results. Note
that even when a query is issued in the conventional way, without
highlighting a term, the history of queries issued
constitutes a form of query context. Yet another source of context
comes from the user who submitted the query. For instance,
the user's bookmarks and browsing history could be used in
selecting the appropriate topic-sensitive rank vectors. These
various sources of search context are discussed in Section 5.
A summary of our approach follows. During the offline processing
of the Web crawl, we generate 16 topic-sensitive PageRank vectors,
each biased (as described in Section 2) using URLs from a top-level
category from the Open Directory Project (ODP) [2]. At query time, we calculate the
similarity of the query (and if available, the query or user
context) to each of these topics. Then instead of using a single
global ranking vector, we take the linear combination of the
topic-sensitive vectors, weighted using the similarities of the
query (and any available context) to the topics. By using a set of rank vectors, we are able to determine
more accurately which pages are truly the most important with
respect to a particular query or query-context. Because the
link-based computations are performed offline, during the
preprocessing stage, the query-time costs are not much greater than
that of the ordinary PageRank algorithm.
2 Review of PageRank
A review of the PageRank algorithm ([16,7,11]) follows. The basic idea of
PageRank is that if page 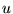 has a link to page
has a link to page 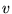 , then the author of
, then the author of 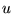 is implicitly conferring some importance to
page
is implicitly conferring some importance to
page 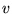 . Intuitively,
Yahoo! is an important page, reflected by the fact that
many pages point to it. Likewise, pages prominently pointed to from
Yahoo! are themselves probably important. How much
importance does a page
. Intuitively,
Yahoo! is an important page, reflected by the fact that
many pages point to it. Likewise, pages prominently pointed to from
Yahoo! are themselves probably important. How much
importance does a page 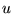 confer to its outlinks? Let
confer to its outlinks? Let 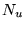 be the outdegree of page
be the outdegree of page
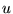 , and let
, and let 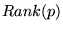 represent the importance
(i.e., PageRank) of page
represent the importance
(i.e., PageRank) of page 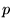 . Then the link
. Then the link 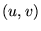 confers
confers
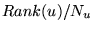 units
of rank to
units
of rank to 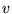 .
This simple idea leads to the following fixpoint computation that
yields the rank vector
.
This simple idea leads to the following fixpoint computation that
yields the rank vector
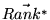 over all
of the pages on the Web. If
over all
of the pages on the Web. If 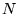 is the number of pages, assign all pages the
initial value
is the number of pages, assign all pages the
initial value 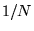 .
Let
.
Let 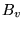 represent the set
of pages pointing to
represent the set
of pages pointing to 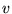 . In
each iteration, propagate the ranks as follows:2
. In
each iteration, propagate the ranks as follows:2
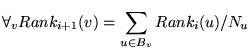
|
(1) |
We continue the iterations until
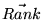 stabilizes
to within some threshold. The final vector
stabilizes
to within some threshold. The final vector
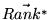 contains
the PageRank vector over the Web. This vector is computed only once
after each crawl of the Web; the values can then be used to
influence the ranking of search results [1].
contains
the PageRank vector over the Web. This vector is computed only once
after each crawl of the Web; the values can then be used to
influence the ranking of search results [1].
The process can also be expressed as the following eigenvector
calculation, providing useful insight into PageRank. Let 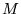 be the square, stochastic
matrix corresponding to the directed graph
be the square, stochastic
matrix corresponding to the directed graph 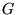 of the Web, assuming all nodes in
of the Web, assuming all nodes in 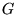 have at least one outgoing
edge. If there is a link from page
have at least one outgoing
edge. If there is a link from page 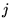 to page
to page 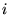 , then let the matrix entry
, then let the matrix entry 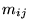 have the value
have the value 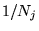 . Let all other entries
have the value 0. One iteration of the
previous fixpoint computation corresponds to the matrix-vector
multiplication
. Let all other entries
have the value 0. One iteration of the
previous fixpoint computation corresponds to the matrix-vector
multiplication
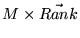 .
Repeatedly multiplying
.
Repeatedly multiplying
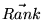 by
by 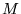 yields the dominant
eigenvector
yields the dominant
eigenvector
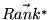 of the
matrix
of the
matrix 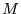 . In
other words,
. In
other words,
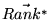 is the
solution to
is the
solution to
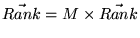 |
(2) |
Because 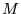 corresponds to the stochastic transition matrix over the graph
corresponds to the stochastic transition matrix over the graph
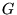 , PageRank can be
viewed as the stationary probability distribution over pages
induced by a random walk on the Web.
, PageRank can be
viewed as the stationary probability distribution over pages
induced by a random walk on the Web.
One caveat is that the convergence of PageRank is guaranteed
only if 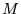 is
irreducible (i.e.,
is
irreducible (i.e., 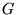 is
strongly connected) and aperiodic [15]. The latter is guaranteed in
practice for the Web, while the former is true if we add a damping
factor
is
strongly connected) and aperiodic [15]. The latter is guaranteed in
practice for the Web, while the former is true if we add a damping
factor 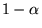 to the rank propagation. We can define
a new matrix
to the rank propagation. We can define
a new matrix 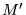 in
which we add transition edges of probability
in
which we add transition edges of probability
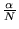 between every pair of nodes in
between every pair of nodes in 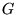 :
:
![$\displaystyle M' = (1-\alpha) M + \alpha [\frac{1}{N}]_{N \times N}$](../../CDROM/refereed/127/img49.png)
|
(3) |
This modification improves the quality of PageRank by introducing a
decay factor 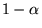 which limits the effect of rank
sinks [6], in
addition to guaranteeing convergence to a unique rank vector.
Substituting
which limits the effect of rank
sinks [6], in
addition to guaranteeing convergence to a unique rank vector.
Substituting 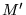 for
for
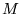 in Equation 2, we can express PageRank as the
solution to:3
in Equation 2, we can express PageRank as the
solution to:3
with
![$ \vec{p} = [\frac{1}{N}]_{N \times 1}$](../../CDROM/refereed/127/img57.png) . The key to
creating topic-sensitive PageRank is that we can bias the
computation to increase the effect of certain categories of pages
by using a nonuniform
. The key to
creating topic-sensitive PageRank is that we can bias the
computation to increase the effect of certain categories of pages
by using a nonuniform
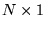 personalization vector for
personalization vector for 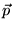 ([6]).4 Note that the biasing involves
introducing additional rank to the appropriate nodes in
each iteration of the computation. It is not simply a
postprocessing step performed on the standard PageRank vector.
([6]).4 Note that the biasing involves
introducing additional rank to the appropriate nodes in
each iteration of the computation. It is not simply a
postprocessing step performed on the standard PageRank vector.
In terms of the random-walk model, the personalization vector
represents the addition of a complete set of transition edges where
the probability on an artificial edge 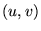 is given by
is given by
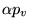 . We will
refer to the solution
. We will
refer to the solution
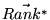 of
Equation 5, with
of
Equation 5, with
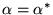 and
a particular
and
a particular
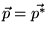 ,
as
,
as
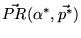 . By appropriately
selecting
. By appropriately
selecting 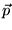 , the rank vector can be made to prefer
certain categories of pages. The bias factor
, the rank vector can be made to prefer
certain categories of pages. The bias factor 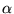 specifies the degree to
which the computation is biased towards
specifies the degree to
which the computation is biased towards 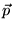 .
.
3 Topic-Sensitive PageRank
3.1 Outline of Approach
In our approach to topic-sensitive PageRank, we precompute the
importance scores offline, as with ordinary PageRank. However, we
compute multiple importance scores for each page; we compute a set
of scores of the importance of a page with respect to various
topics. At query time, these importance scores are combined based
on the topics of the query to form a composite PageRank score for
those pages matching the query. This score can be used in
conjunction with other IR-based scoring schemes to produce a final
rank for the result pages with respect to the query. As the scoring
functions of commercial search engines are not known, in our work
we do not consider the effect of these other IR scores.5 We believe that the improvements
to PageRank's precision will translate into improvements in overall
search rankings, even after other IR-based scores are factored
in.6
3.2 ODP-biasing
The first step in our approach is to generate a set of biased
PageRank vectors using a set of ``basis'' topics. This step is
performed once, offline, during the preprocessing of the Web crawl.
For the personalization vector 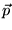 described in Section 2, we use the URLs present in the
various categories in the ODP. We create 16 different biased
PageRank vectors by using the URLs present below each of the 16 top
level categories of the ODP as the personalization vectors. In
particular, let
described in Section 2, we use the URLs present in the
various categories in the ODP. We create 16 different biased
PageRank vectors by using the URLs present below each of the 16 top
level categories of the ODP as the personalization vectors. In
particular, let 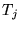 be
the set of URLs in the ODP category
be
the set of URLs in the ODP category 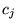 . Then when computing the PageRank vector for
topic
. Then when computing the PageRank vector for
topic 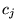 , in place of the
uniform damping vector
, in place of the
uniform damping vector
![$ \vec{p} = [\frac{1}{N}]_{N \times 1}$](../../CDROM/refereed/127/img76.png) , we use the
nonuniform vector
, we use the
nonuniform vector
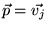 where
where
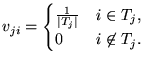
|
(6) |
The PageRank vector for topic 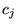 will be referred to as
will be referred to as
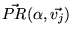 . We also generate
the single unbiased PageRank vector (denoted as
NOBIAS) for the purpose of
comparison. The choice of
. We also generate
the single unbiased PageRank vector (denoted as
NOBIAS) for the purpose of
comparison. The choice of 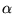 will be discussed in Section 4.1.
will be discussed in Section 4.1.
We also compute the 16 class term-vectors 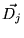 consisting of the
terms in the documents below each of the 16 top level categories.
consisting of the
terms in the documents below each of the 16 top level categories.
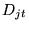 simply gives
the total number of occurrences of term
simply gives
the total number of occurrences of term 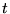 in documents listed below class
in documents listed below class 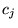 of the ODP.
of the ODP.
One could envision using other sources for creating
topic-sensitive PageRank vectors; however, the ODP data is freely
available, and as it is compiled by thousands of volunteer editors,
is less susceptible to influence by any one party.7
3.3 Query-Time Importance Score
The second step in our approach is performed at query time.
Given a query 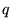 , let
, let
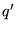 be the context of
be the context of
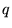 . In other words, if
the query was issued by highlighting the term
. In other words, if
the query was issued by highlighting the term 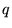 in some Web page
in some Web page 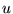 , then
, then 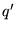 consists of the terms in
consists of the terms in 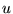 . For ordinary queries not done
in context, let
. For ordinary queries not done
in context, let 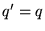 . Using a unigram language model, with parameters
set to their maximum-likelihood estimates, we compute
the class probabilities for
each of the 16 top level ODP classes, conditioned on
. Using a unigram language model, with parameters
set to their maximum-likelihood estimates, we compute
the class probabilities for
each of the 16 top level ODP classes, conditioned on 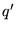 . Let
. Let 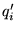 be the
be the 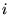 th term in the query (or query context)
th term in the query (or query context) 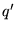 . Then given the query
. Then given the query 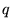 , we compute for each
, we compute for each 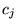 the following:
the following:
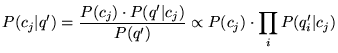
|
(7) |
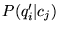 is
easily computed from the class term-vector
is
easily computed from the class term-vector 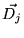 . The quantity
. The quantity 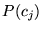 is not as straightforward. We chose to
make it uniform, although we could personalize the query results
for different users by varying this distribution. In other
words, for some user
is not as straightforward. We chose to
make it uniform, although we could personalize the query results
for different users by varying this distribution. In other
words, for some user  , we
can use a prior distribution
, we
can use a prior distribution 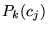 that reflects the interests of user
that reflects the interests of user
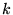 . This method
provides an alternative framework for user-based personalization,
rather than directly varying the damping vector
. This method
provides an alternative framework for user-based personalization,
rather than directly varying the damping vector 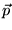 as had been suggested
in [7,6].
as had been suggested
in [7,6].
Using a text index, we retrieve URLs for all documents
containing the original query terms 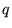 . Finally, we compute the
query-sensitive importance score of each of these retrieved URLs as
follows. Let
. Finally, we compute the
query-sensitive importance score of each of these retrieved URLs as
follows. Let 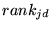 be the rank of document
be the rank of document 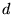 given by the rank vector
given by the rank vector
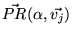 (i.e., the rank
vector for topic
(i.e., the rank
vector for topic 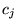 ).
For the Web document
).
For the Web document 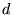 , we
compute the query-sensitive importance score
, we
compute the query-sensitive importance score 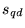 as follows.
as follows.
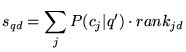
|
(8) |
The results are ranked according to this composite score 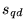 .8
.8
The above query-sensitive PageRank computation has the following
probabilistic interpretation, in terms of the ``random surfer''
model [7]. Let 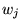 be the coefficient used to
weight the
be the coefficient used to
weight the 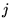 th
rank vector, with
th
rank vector, with
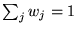 (e.g., let
(e.g., let
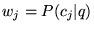 ). Then note that the
equality
). Then note that the
equality
![$\displaystyle \sum_j [w_j \vec{PR}(\alpha, \vec{v_j})] = \vec{PR}\bigl(\alpha, \sum_j [w_j \vec{v_j}]\bigr)$](../../CDROM/refereed/127/img123.png)
|
(9) |
holds, as shown in Appendix A. Thus we see that the following
random walk on the Web yields the topic-sensitive score 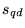 . With probability
. With probability 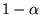 , a random surfer on
page
, a random surfer on
page 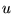 follows an outlink
of
follows an outlink
of 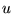 (where the
particular outlink is chosen uniformly at random). With probability
(where the
particular outlink is chosen uniformly at random). With probability
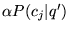 , the surfer instead jumps
to one of the pages in
, the surfer instead jumps
to one of the pages in 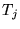 (where the particular page in
(where the particular page in 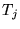 is chosen uniformly at
random). The long term visit probability that the surfer is at page
is chosen uniformly at
random). The long term visit probability that the surfer is at page
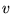 is exactly given
by the composite score
is exactly given
by the composite score 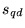 defined above. Thus, topics exert
influence over the final score in proportion to their affinity with
the query (or query context).
defined above. Thus, topics exert
influence over the final score in proportion to their affinity with
the query (or query context).
4 Experimental Results
To measure the behavior of topic-sensitive PageRank, we
conducted a series of experiments. In Section 4.1 we describe the similarity
measure we use to compare two rankings. In Section 4.2, we investigate how the induced
rankings vary, based on both the topic used to bias the rank
vectors as well as the choice of the bias factor 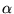 . In Section 4.3, we present results of a user
study showing the retrieval performance of ordinary PageRank versus
topic-sensitive PageRank. Finally, in Section 4.4, we provide an initial look at how
the use of query context can be used in conjunction with
topic-sensitive PageRank.
. In Section 4.3, we present results of a user
study showing the retrieval performance of ordinary PageRank versus
topic-sensitive PageRank. Finally, in Section 4.4, we provide an initial look at how
the use of query context can be used in conjunction with
topic-sensitive PageRank.
As a source of Web data, we used the latest Web crawl from the
Stanford WebBase [12],
performed in January 2001, containing roughly 120 million pages.
Our crawl contained roughly 280,000 of the 3 million URLs in the
ODP. For our experiments, we used 35 of the sample queries given
in [9], which were in turn
compiled from earlier papers.9 The
queries are listed in Table 1.
Table 1: Queries used
| affirmative action |
lipari |
| alcoholism |
lyme disease |
| amusement
parks |
mutual
funds |
| architecture |
national
parks |
| bicycling |
parallel
architecture |
| blues |
recycling
cans |
| cheese |
rock
climbing |
| citrus
groves |
san
francisco |
| classical
guitar |
shakespeare |
| computer
vision |
stamp
collecting |
| cruises |
sushi |
| death
valley |
table
tennis |
| field
hockey |
telecommuting |
| gardening |
vintage
cars |
| graphic
design |
volcano |
| gulf war |
zen
buddhism |
| hiv |
zener |
| java |
|
4.1 Similarity Measure for Induced Rankings
We use two measures when comparing rankings. The first measure,
denoted
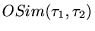 , indicates the degree of
overlap between the top
, indicates the degree of
overlap between the top 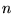 URLs of two rankings,
URLs of two rankings, 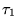 and
and 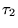 . We define the overlap of two sets
. We define the overlap of two sets 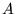 and
and 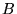 (each of size
(each of size 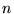 ) to be
) to be
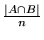 . In our
comparisons we will use
. In our
comparisons we will use 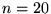 . The overlap measure
. The overlap measure 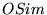 gives an incomplete
picture of the similarity of two rankings, as it does not indicate
the degree to which the relative orderings of the top
gives an incomplete
picture of the similarity of two rankings, as it does not indicate
the degree to which the relative orderings of the top 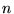 URLs of two rankings are in
agreement. Therefore, we also use a variant of the Kendall's
URLs of two rankings are in
agreement. Therefore, we also use a variant of the Kendall's 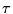 distance measure.
See [9] for a discussion of
various distance measures for ranked lists in the context of Web
search results. For consistency with
distance measure.
See [9] for a discussion of
various distance measures for ranked lists in the context of Web
search results. For consistency with  , we will present our definition as a
similarity (as opposed to distance) measure, so that values closer
to 1 indicate closer agreement. Consider two partially ordered
lists of URLs,
, we will present our definition as a
similarity (as opposed to distance) measure, so that values closer
to 1 indicate closer agreement. Consider two partially ordered
lists of URLs, 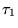 and
and 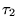 , each of length
, each of length 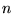 . Let
. Let 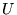 be the union of the URLs in
be the union of the URLs in 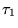 and
and 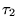 . If
. If 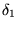 is
is
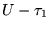 , then let
, then let
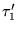 be the
extension of
be the
extension of 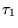 , where
, where 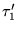 contains
contains 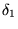 appearing after all the URLs in
appearing after all the URLs in 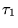 .10We extend
.10We extend 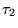 analogously to yield
analogously to yield 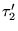 . We define our
similarity measure
. We define our
similarity measure 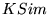 as follows:
as follows:
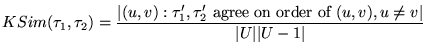
|
(10) |
In other words,
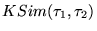 is the probability that
is the probability that 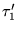 and
and 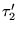 agree on the relative ordering of a
randomly selected pair of distinct nodes
agree on the relative ordering of a
randomly selected pair of distinct nodes
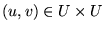 .
.
4.2 Effect of ODP-Biasing
In this section we measure the effects of topically biasing the
PageRank computation. Firstly, note that the choice of the bias
factor 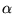 , discussed in Section 2, affects the degree to which the
resultant vector is biased towards the topic vector used for
, discussed in Section 2, affects the degree to which the
resultant vector is biased towards the topic vector used for 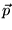 . Consider the extreme
cases. For
. Consider the extreme
cases. For 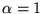 , the URLs in the bias set
, the URLs in the bias set 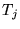 will be assigned the score
will be assigned the score
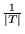 , and all other URLs
receive the score 0. Conversely, as
, and all other URLs
receive the score 0. Conversely, as 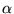 tends to 0, the content of
tends to 0, the content of 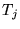 becomes irrelevant to the
final score assignment.
becomes irrelevant to the
final score assignment.
We chose to use
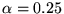 heuristically, after inspecting the rankings for several of the
queries listed in Table 1. We did not concentrate on
optimizing
heuristically, after inspecting the rankings for several of the
queries listed in Table 1. We did not concentrate on
optimizing 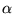 , as we discovered that the induced
rankings of query results are not very sensitive to the choice of
, as we discovered that the induced
rankings of query results are not very sensitive to the choice of
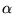 . For
instance, for
. For
instance, for
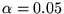 and
and
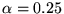 , we
measured the average similarity of the induced rankings across our
set of test queries, for each of our PageRank vectors.11 The results are given in
Table 2. We see that the
average overlap between the top 20 results for the two values of
, we
measured the average similarity of the induced rankings across our
set of test queries, for each of our PageRank vectors.11 The results are given in
Table 2. We see that the
average overlap between the top 20 results for the two values of
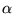 is very high.
Furthermore, the high values for
is very high.
Furthermore, the high values for  indicate high overlap as well agreement (on
average) on the relative ordering of these top 20 URLs for the two
values of
indicate high overlap as well agreement (on
average) on the relative ordering of these top 20 URLs for the two
values of 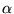 . All subsequent experiments use
. All subsequent experiments use
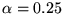 .
.
Table 2: Average similarity of rankings for
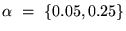
| Bias Set |
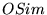 |
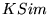 |
| NOBIAS |
0.72 |
0.64 |
| ARTS |
0.66 |
0.58 |
| BUSINESS |
0.63 |
0.54 |
| COMPUTERS |
0.70 |
0.60 |
| GAMES |
0.78 |
0.67 |
| HEALTH |
0.73 |
0.62 |
| HOME |
0.77 |
0.67 |
| KIDS &
TEENS |
0.74 |
0.66 |
| NEWS |
0.74 |
0.65 |
| RECREATION |
0.62 |
0.55 |
| REFERENCE |
0.68 |
0.57 |
| REGIONAL |
0.60 |
0.52 |
| SCIENCE |
0.69 |
0.59 |
| SHOPPING |
0.66 |
0.55 |
| SOCIETY |
0.57 |
0.50 |
| SPORTS |
0.69 |
0.60 |
| WORLD |
0.64 |
0.55 |
The differences across different topically-biased
PageRank vectors is much higher, dwarfing any variations caused by
the choice of 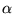 . We computed the average, across our test
queries, of the pairwise similarity between the rankings induced by
the different topically-biased vectors. The 5 most similar pairs,
according to our
. We computed the average, across our test
queries, of the pairwise similarity between the rankings induced by
the different topically-biased vectors. The 5 most similar pairs,
according to our 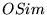 measure, are given in Table 3, showing that even the most
similar topically-biased rankings have little overlap.
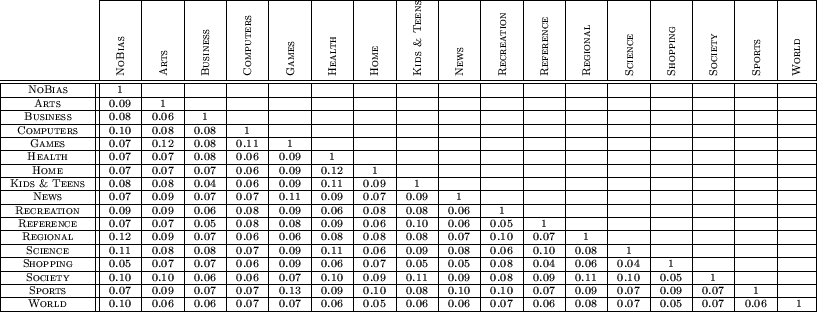
Table 4 shows that the
pairwise similarities of the rankings induced by the other ranking
vectors are close to 0. Having established that the
topically-biased PageRank vectors each rank the results
substantially differently, we proceed to investigate which of these
rankings is ``best'' for specific queries.
measure, are given in Table 3, showing that even the most
similar topically-biased rankings have little overlap.
Table 4 shows that the
pairwise similarities of the rankings induced by the other ranking
vectors are close to 0. Having established that the
topically-biased PageRank vectors each rank the results
substantially differently, we proceed to investigate which of these
rankings is ``best'' for specific queries.
Table 3: Topic pairs yielding most
similar rankings
| Bias-Topic Pair |
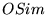 |
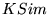 |
| (GAMES,
SPORTS) |
0.18 |
0.13 |
| (NOBIAS,
REGIONAL) |
0.18 |
0.12 |
| (KIDS & TEENS,
SOCIETY) |
0.18 |
0.11 |
| (HEALTH,
HOME) |
0.17 |
0.12 |
| (HEALTH, KIDS
& TEENS) |
0.17 |
0.11 |
Table 4: Pairwise comparison of
topically-biased rankings (
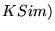
|
As an example, Table 5 shows the top 5 ranked URLs
for the query ``bicycling,'' using each of the topically-biased
PageRank vectors. Note in particular that the ranking induced by
the SPORTS-biased vector is of high quality.12 Also note that the ranking
induced by the SHOPPING-biased vector leads to the
high ranking of websites selling bicycle-related accessories.
Table 5: Query ``bicycling''
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.3 Query-Sensitive Scoring
In this section we look at how effectively we can utilize the
ranking precision gained by the use of multiple PageRank vectors.
Given a query, our first task is to determine which of the rank
vectors can best rank the results for the query. We found that
simply using 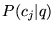 as discussed in
Section 3.3 yielded
intuitive results for determining which topics are most closely
associated with a query. In particular, for most of the test
queries, the ODP categories with the highest values for
as discussed in
Section 3.3 yielded
intuitive results for determining which topics are most closely
associated with a query. In particular, for most of the test
queries, the ODP categories with the highest values for 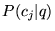 are intuitively
the most relevant categories for the query. In Table 6, we list for each test query, the
3 categories with the highest values for
are intuitively
the most relevant categories for the query. In Table 6, we list for each test query, the
3 categories with the highest values for 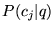 . When computing the composite
. When computing the composite
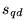 score in our
experiments, we chose to use the weighted sum of only the rank
vectors associated with the three topics with the highest values
for
score in our
experiments, we chose to use the weighted sum of only the rank
vectors associated with the three topics with the highest values
for 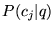 ,
rather than all of the topics. Based on the data in Table 6, we saw no need to include the
scores from the topic vectors with lower associated values for
,
rather than all of the topics. Based on the data in Table 6, we saw no need to include the
scores from the topic vectors with lower associated values for
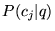 .
.
To compare our query-sensitive approach to ordinary PageRank, we
conducted a user study. We randomly selected 10 queries from our
test set for the study, and found 5 volunteers. For each query, the
volunteer was shown 2 result rankings; one consisted of the top 10
results satisfying the query, when these results were ranked with
the unbiased PageRank vector, and the other consisted of the top 10
results for the query when the results were ranked with the
composite 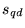 score.13The volunteer was asked to select
all URLs which were ``relevant'' to the query, in their opinion.
Furthermore, they were asked to say which of the two rankings was
``better'' overall, in their opinion. They were not told anything
about how either of the rankings was generated. The rankings
induced by the topic-sensitive PageRank score
score.13The volunteer was asked to select
all URLs which were ``relevant'' to the query, in their opinion.
Furthermore, they were asked to say which of the two rankings was
``better'' overall, in their opinion. They were not told anything
about how either of the rankings was generated. The rankings
induced by the topic-sensitive PageRank score 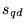 were significantly
preferred by our test group. Let a URL be considered
relevant if at least 3 of the 5 volunteers selected it as
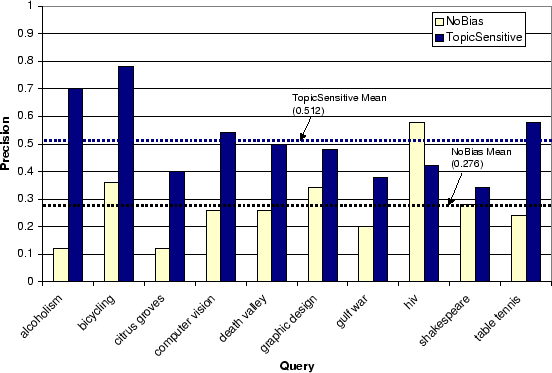
relevant for the query. The precision then is the fraction
of the top 10 URLs that are deemed relevant. The precision
of the two ranking techniques for each test query is shown in
Figure 1. The average
precision for the rankings induced by the topic-sensitive PageRank
scores is substantially higher than that of the unbiased PageRank
scores. Furthermore, as shown in Table 7, for nearly all queries, a
majority of the users preferred the rankings induced by the
topic-sensitive PageRank scores. These results suggest that the
effectiveness of a query-result scoring function can be improved by
the use of a topic-sensitive PageRank scheme in place of a generic
PageRank scheme.
were significantly
preferred by our test group. Let a URL be considered
relevant if at least 3 of the 5 volunteers selected it as
relevant for the query. The precision then is the fraction
of the top 10 URLs that are deemed relevant. The precision
of the two ranking techniques for each test query is shown in
Figure 1. The average
precision for the rankings induced by the topic-sensitive PageRank
scores is substantially higher than that of the unbiased PageRank
scores. Furthermore, as shown in Table 7, for nearly all queries, a
majority of the users preferred the rankings induced by the
topic-sensitive PageRank scores. These results suggest that the
effectiveness of a query-result scoring function can be improved by
the use of a topic-sensitive PageRank scheme in place of a generic
PageRank scheme.
Table 6: Estimates for
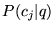
| affirmative action |
| NEWS |
0.41 |
| SOCIETY |
0.22 |
| REFERENCE |
0.17 |
|
|
| alcoholism |
| HEALTH |
0.47 |
| KIDS & TEENS |
0.20 |
| ARTS |
0.06 |
|
|
| amusement parks |
| REGIONAL |
0.51 |
| RECREATION |
0.23 |
| KIDS & TEENS |
0.08 |
|
|
| architecture |
| COMPUTERS |
0.26 |
| REFERENCE |
0.19 |
| BUSINESS |
0.09 |
|
|
| bicycling |
| SPORTS |
0.52 |
| REGIONAL |
0.13 |
| HEALTH |
0.07 |
|
|
| blues |
| ARTS |
0.52 |
| SHOPPING |
0.12 |
| NEWS |
0.08 |
|
|
| cheese |
| HOME |
0.72 |
| RECREATION |
0.10 |
| SHOPPING |
0.05 |
|
|
| citrus groves |
| SHOPPING |
0.34 |
| HOME |
0.21 |
| REGIONAL |
0.18 |
|
|
| classical guitar |
| ARTS |
0.75 |
| SHOPPING |
0.21 |
| NEWS |
0.01 |
|
|
| computer vision |
| COMPUTERS |
0.24 |
| BUSINESS |
0.14 |
| REFERENCE |
0.09 |
|
|
| cruises |
| RECREATION |
0.65 |
| REGIONAL |
0.18 |
| SPORTS |
0.04 |
|
|
| death valley |
| REGIONAL |
0.28 |
| SOCIETY |
0.14 |
| NEWS |
0.10 |
|
|
| field hockey |
| SPORTS |
0.89 |
| SHOPPING |
0.03 |
| REFERENCE |
0.03 |
|
|
| gardening |
| HOME |
0.63 |
| SHOPPING |
0.14 |
| REGIONAL |
0.04 |
|
|
| graphic design |
| COMPUTERS |
0.36 |
| BUSINESS |
0.23 |
| SHOPPING |
0.09 |
|
|
| gulf
war |
| SOCIETY |
0.21 |
| KIDS & TEENS |
0.18 |
| REGIONAL |
0.17 |
|
|
| hiv |
| HEALTH |
0.40 |
| NEWS |
0.19 |
| KIDS & TEENS |
0.14 |
|
|
| java |
| COMPUTERS |
0.53 |
| GAMES |
0.10 |
| KIDS & TEENS |
0.06 |
|
|
| lipari |
| HOME |
0.19 |
| KIDS & TEENS |
0.17 |
| NEWS |
0.13 |
|
|
| lyme
disease |
| HEALTH |
0.96 |
| REGIONAL |
0.01 |
| RECREATION |
0.01 |
|
|
| mutual funds |
| BUSINESS |
0.77 |
| REGIONAL |
0.05 |
| HOME |
0.05 |
|
|
| national parks |
| REGIONAL |
0.42 |
| RECREATION |
0.16 |
| KIDS & TEENS |
0.09 |
|
|
| parallel architecture |
| COMPUTERS |
0.70 |
| SCIENCE |
0.10 |
| REFERENCE |
0.07 |
|
|
| recycling cans |
| HOME |
0.42 |
| BUSINESS |
0.38 |
| KIDS & TEENS |
0.06 |
|
|
| rock
climbing |
| RECREATION |
0.54 |
| REGIONAL |
0.13 |
| SPORTS |
0.07 |
|
|
| san
francisco |
| SPORTS |
0.27 |
| REGIONAL |
0.16 |
| RECREATION |
0.10 |
|
|
| shakespeare |
| ARTS |
0.34 |
| REFERENCE |
0.21 |
| KIDS & TEENS |
0.15 |
|
|
| stamp collecting |
| SHOPPING |
0.44 |
| RECREATION |
0.39 |
| SCIENCE |
0.02 |
|
|
| sushi |
| HOME |
0.56 |
| KIDS & TEENS |
0.13 |
| SHOPPING |
0.07 |
|
|
| table tennis |
| SPORTS |
0.53 |
| SHOPPING |
0.14 |
| REGIONAL |
0.09 |
|
|
| telecommuting |
| BUSINESS |
0.70 |
| KIDS & TEENS |
0.04 |
| SOCIETY |
0.03 |
|
|
| vintage cars |
| SHOPPING |
0.67 |
| RECREATION |
0.23 |
| HOME |
0.02 |
|
|
| volcano |
| SCIENCE |
0.36 |
| REGIONAL |
0.18 |
| RECREATION |
0.13 |
|
| zen
buddhism |
| SOCIETY |
0.88 |
| KIDS & TEENS |
0.09 |
| WORLD |
0.01 |
|
| zener |
| KIDS & TEENS |
0.17 |
| NEWS |
0.13 |
| BUSINESS |
0.11 |
|
|
Figure 1: Precision @ 10
results for our test queries. The average precision over the ten
queries is also shown.
|
Table 7: Ranking preferred by majority of users
| Query |
Preferred by
Majority |
| alcoholism |
TOPICSENSITIVE |
| bicycling |
TOPICSENSITIVE |
| citrus groves |
TOPICSENSITIVE |
| computer vision |
TOPICSENSITIVE |
| death valley |
TOPICSENSITIVE |
| graphic design |
TOPICSENSITIVE |
| gulf war |
TOPICSENSITIVE |
| hiv |
NOBIAS |
| shakespeare |
Neither |
| table tennis |
TOPICSENSITIVE |
4.4 Context-Sensitive Scoring
In Section 4.3, the
topic-sensitive ranking vectors were chosen using the topics most
strongly associated with the query term. If the search is done in
context, for instance by highlighting a term in a Web page and
invoking a search, then the context can be used instead of the
query to determine the topics. Using the context can help
disambiguate the query term and yield results that more closely
reflect the intent of the user. We now illustrate with an example
how using query-context can help a system which uses
topic-sensitive PageRank.
Consider the query ``blues'' taken from our test set. This term
has several different senses; for instance it could refer to a
musical genre, or to a form of depression. Two Web pages in which
the term is used with these different senses, as well as short
textual excerpts from the pages, are shown in Table 8. Consider the case where a
user reading one of these two pages highlights the term ``blues''
to submit a search query. At query time, the first step of our
system is to determine which topic best applies to the query in
context. Thus, we calculate 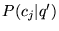 as described in Section 3.3, using for
as described in Section 3.3, using for 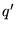 the terms of the entire
page, rather than just the term ``blues.'' For the first page
(discussing music),
the terms of the entire
page, rather than just the term ``blues.'' For the first page
(discussing music),
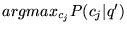 is
ARTS, and for the second page (discussing
depression),
is
ARTS, and for the second page (discussing
depression),
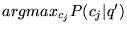 is
HEALTH. The next step is to use a text index to
fetch a list of URLs for all documents containing the term
``blues'' -- the highlighted term for which the query was issued.
Finally, the URLs are ranked using the appropriate ranking vector
that was selected using the
is
HEALTH. The next step is to use a text index to
fetch a list of URLs for all documents containing the term
``blues'' -- the highlighted term for which the query was issued.
Finally, the URLs are ranked using the appropriate ranking vector
that was selected using the 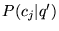 values (i.e., either
ARTS or HEALTH). Table 9 shows the top 5 URLs for
the query ``blues'' using the topic-sensitive PageRank vectors for
ARTS, HEALTH, and
NOBIAS. We see that as desired, most
of the results ranked using the ARTS-biased vector
are pages discussing music, while all of the top results ranked
using the HEALTH-biased vector discuss depression.
The context of the query allows the system to pick the appropriate
topic-sensitive ranking vector, and yields search results
reflecting the appropriate sense of the search term.
values (i.e., either
ARTS or HEALTH). Table 9 shows the top 5 URLs for
the query ``blues'' using the topic-sensitive PageRank vectors for
ARTS, HEALTH, and
NOBIAS. We see that as desired, most
of the results ranked using the ARTS-biased vector
are pages discussing music, while all of the top results ranked
using the HEALTH-biased vector discuss depression.
The context of the query allows the system to pick the appropriate
topic-sensitive ranking vector, and yields search results
reflecting the appropriate sense of the search term.
Table 8: Two different search contexts
for the query ``blues''
| That Blues Music
Page |
Postpartum Depression & the `Baby
Blues' |
| http://www.fred.net/turtle/blues.shtml |
http://familydoctor.org/handouts/379.html |
| ...If you're stuck for new material, visit Dan
Bowden's Blues and Jazz Transcriptions - lots of older blues guitar
transcriptions for you historic blues fans ... |
...If you're a new mother and have any of these
symptoms, you have what is called the ``baby blues.'' ``The blues''
are considered a normal part of early motherhood and usually go
away within 10 days after delivery. However, some women have worse
symptoms or symptoms last longer. This is called ``postpartum
depression.'' ... |
Table 9: Results for query
``blues''
|
|
|
|
|
|
|
5 Sources of Search Context
In the previous section, we discussed one possible source of
context to utilize in the generation of the composite PageRank
score, namely the document containing the query term highlighted by
the user. There are a variety of other sources of context that may
be used in our scheme. For instance, the history of queries issued
leading up to the current query is another form of query context. A
search for ``basketball'' followed up with a search for ``Jordan''
presents an opportunity for disambiguating the latter. As another
example, most modern search engines incorporate some sort of
hierarchical directory, listing URLs for a small subset of the Web,
as part of their search interface.14 The current node in the
hierarchy that the user is browsing at constitutes a source of
query context. When browsing URLs at
TOP/ARTS, for instance, any queries
issued could have search results (from the entire Web index) ranked
with the ARTS rank vector, rather than either
restricting results to URLs listed in that particular category, or
not making use of the category whatsoever. In addition to these
types of context associated with the query itself, we can also
potentially utilize query independent user context.
Sources of user context include the users' browsing patterns,
bookmarks, and email archives. As mentioned in Section 3.3, we can integrate user context by
selecting a nonuniform prior, 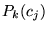 , based on how closely the user's
context accords with each of the basis topics.
, based on how closely the user's
context accords with each of the basis topics.
When attempting to utilize the aforementioned sources of search
context, mediating the personalization of PageRank via a set of
basis topics yields several benefits over attempting to explicitly
choose a personalization vector directly.
- Flexibility: For any kind of context, we can compute the
context-sensitive PageRank score by using a classifier to compute
the similarity of the context with the basis topics and then
weighting the topic-sensitive PageRank vectors appropriately. We
can treat such diverse sources of search context such as email,
bookmarks, browsing history, and query history uniformly.
- Transparency: The topically-biased rank vectors have
intuitive interpretations. If we see that our system is giving
undue preference to certain topics, we can tune the classifier used
on the search context, or adjust topic weights manually. When
utilizing user context, the users themselves can be shown what
topics the system believes represent their interests.
- Privacy: Certain forms of search context raise potential
privacy concerns. Clearly it is inappropriate to send the user's
browsing history or other personal information to the search-engine
server for use in constructing a profile. However a
client-side program could use the user context to generate
the user profile locally, and send only the summary information,
consisting of the weights assigned to the basis topics, over to the
server. The amount of privacy lost in knowing only that the user's
browsing pattern suggests that he is interested in
COMPUTERS with weight 0.5 is much less than actually
obtaining his browser's history cache. When making use of
query-context, if the user is browsing sensitive personal
documents, they would be more comfortable if the search client sent
to the server topic weights rather than the actual document text
surrounding the highlighted query term.
- Efficiency: For a small number of basis topics (such as
the 16 ODP categories), both the query-time cost and the offline
preprocessing cost of our approach is low, and practical to
implement with current Web indexing infrastructure.
A wide variety search-context sources exist which, if utilized
appropriately, can help users better manage the deluge of
information they are faced with. Although we have begun exploring
how best to make use of available context, much work remains in
identifying and utilizing search context with the goal of
personalizing Web search.
6 Ongoing Work
We are currently exploring several ways of improving our
approach for topic-sensitive PageRank. As discussed in the previous
section, discovering sources of search context is a ripe area of
research. Another area of investigation is the development of the
best set of basis topics. For instance it may be worthwhile to use
a finer-grained set of topics, perhaps using the second or third
level of the Open Directory hierarchy, rather than simply the top
level. However, a fine-grained set of topics leads to efficiency
considerations, as the cost of the naive approach to computing
these topic-sensitive vectors is linear in the number of basis
topics. See [13] for approaches
that may make the use of a larger, finer grained set of basis
topics practical.
We are also currently investigating a different approach to
creating the damping vector 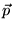 used to create the topic-sensitive rank
vectors. This approach has the potential of being more resistant to
adversarial ODP editors. Currently, as described in Section 3.2, we set the damping vector
used to create the topic-sensitive rank
vectors. This approach has the potential of being more resistant to
adversarial ODP editors. Currently, as described in Section 3.2, we set the damping vector
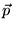 for topic
for topic
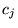 to
to 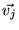 , where
, where 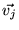 is defined in
Equation 6. In the modified
approach, we instead first train a classifier for the basis set of
topics using the ODP data as our training set, and then assign to
all pages on the Web a distribution of topic weights.15Let this topic weight of a page
is defined in
Equation 6. In the modified
approach, we instead first train a classifier for the basis set of
topics using the ODP data as our training set, and then assign to
all pages on the Web a distribution of topic weights.15Let this topic weight of a page
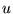 for category
for category 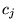 be
be 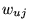 . Then we replace Equation 6 with
. Then we replace Equation 6 with
![$\displaystyle \forall_{i \in Web} [v_{ji} = \frac{w_{ij}}{\sum_k w_{kj}}]$](../../CDROM/refereed/127/img221.png)
|
(11) |
In this way, we hope to ensure that the PageRank vectors generated
are not overly sensitive to particular choices made by individual
ODP editors.
We plan to investigate the above enhancements to generating the
topic-sensitive PageRank score, and evaluate their effect on
retrieval performance, both in isolation and when combined with
typical IR scoring functions.
7 Acknowledgments
I would like to thank Professor Jeff Ullman for invaluable
comments and feedback. I would like to thank Glen Jeh and Professor
Jennifer Widom for several useful discussions. I would also like to
thank Aristides Gionis for his feedback. Finally, I would like to
thank the anonymous reviewers for their insightful comments.
- 1
- The Google Search Engine: Commercial search engine founded by
the originators of PageRank.
http://www.google.com/.
- 2
- The Open Directory Project: Web directory for over 2.5 million
URLs.
http://www.dmoz.org/.
- 3
- `More Evil Than Dr. Evil?'
http://searchenginewatch.com/sereport/99/11-google.html.
- 4
- Krishna Bharat and Monika R. Henzinger.
Improved algorithms for topic distillation in a hyperlinked
environment.
In Proceedings of the ACM-SIGIR, 1998.
- 5
- Krishna Bharat and George A. Mihaila.
When experts agree: Using non-affiliated experts to rank popular
topics.
In Proceedings of the Tenth International World Wide Web
Conference, 2001.
- 6
- Sergey Brin, Rajeev Motwani, Larry Page, and Terry
Winograd.
What can you do with a web in your pocket.
In Bulletin of the IEEE Computer Society Technical Committee on
Data Engineering, 1998.
- 7
- Sergey Brin and Larry Page.
The anatomy of a large-scale hypertextual web search engine.
In Proceedings of the Seventh International World Wide Web
Conference, 1998.
- 8
- S. Chakrabarti, B. Dom, D. Gibson,
J. Kleinberg, P. Raghavan, and S. Rajagopalan.
Automatic resource compilation by analyzing hyperlink structure and
associated text.
In Proceedings of the Seventh International World Wide Web Conference,
1998.
- 9
- Cynthia Dwork, Ravi Kumar, Moni Naor, and
D. Sivakumar.
Rank aggregation methods for the web.
In Proceedings of the Tenth International World Wide Web
Conference, 2001.
- 10
- Lev Finkelstein, Evgeniy Gabrilovich, Yossi Matias, Ehud
Rivlin, Zach Solan, Gadi Wolfman, and Eytan Ruppin.
Placing search in context: the concept revisited.
In Proceedings of the Tenth International World Wide Web
Conference, 2001.
- 11
- Taher H. Haveliwala.
Efficient computation of PageRank.
Stanford University Technical Report, 1999.
- 12
- J. Hirai, S. Raghavan, H. Garcia-Molina, and
A. Paepcke.
WebBase: A repository of web pages.
In Proceedings of the Ninth International World Wide Web
Conference, 2000.
- 13
- Glen Jeh and Jennifer Widom.
Scaling personalized web search.
Stanford University Technical Report, 2002.
- 14
- Jon Kleinberg.
Authoritative sources in a hyperlinked environment.
In Proceedings of the ACM-SIAM Symposium on Discrete
Algorithms, 1998.
- 15
- Rajeev Motwani and Prabhakar Raghavan.
Randomized Algorithms.
Cambridge University Press, United Kingdom, 1995.
- Larry Page.
PageRank: Bringing order to the web.
Stanford Digital Libraries Working Paper, 1997.
- 17
- Davood Rafiei and Alberto O. Mendelzon.
What is this page known for? Computing web page reputations.
In Proceedings of the Ninth International World Wide Web
Conference, 2000.
- 18
- Matthew Richardson and Pedro Domingos.
The Intelligent Surfer: Probabilistic Combination of Link and
Content Information in PageRank, volume 14.
MIT Press, Cambridge, MA, 2002 (To appear).
Appendix
A. Weighted Sum of PageRank Vectors
In this section we derive the interpretation of the weighted sum
of PageRank vectors.16
Consider a set of rank vectors
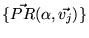 for some fixed
for some fixed
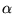 .17 For brevity let
.17 For brevity let
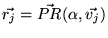 .
Furthermore let
.
Furthermore let
![$ \vec{r'} = \sum_j [w_j \vec{r_j}]$](../../CDROM/refereed/127/img225.png) , and
, and
![$ \vec{v'} = \sum_j [w_j \vec{v_j}]$](../../CDROM/refereed/127/img226.png) . We claim that
. We claim that
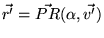 . In other
words,
. In other
words, 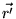 is itself a PageRank vector, where the
personalization vector
is itself a PageRank vector, where the
personalization vector 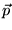 is set to
is set to 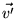 . The proof follows.
. The proof follows.
Because each 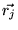 satisfies Equation 5 (with
satisfies Equation 5 (with
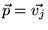 ), we have that
), we have that
Thus 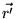 satisfies Equation 5 for the personalization vector
satisfies Equation 5 for the personalization vector
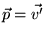 ,
and our proof is complete.
,
and our proof is complete.
Footnotes
- 1
- Supported by NSF Grant IIS-0085896 and an NSF Graduate Research
Fellowship.
- 2
- Note that for
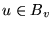 , the edge
, the edge 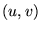 guarantees
guarantees
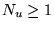 .
.
- 3
- Equation 5 makes use of
the fact that
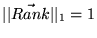 .
.
- 4
- A minor caveat: to ensure that
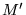 is irreducible when
is irreducible when 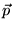 contains any 0 entries, nodes not
reachable from nonzero nodes in
contains any 0 entries, nodes not
reachable from nonzero nodes in 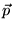 should be removed. In practice this is
not problematic.
should be removed. In practice this is
not problematic.
- 5
- For instance, most search engines use term weighting schemes
which make special use of HTML tags.
- 6
- Note that the topic-sensitive PageRank score itself implicitly
makes use of IR in determining the topic of the query.
However this use of IR is not vulnerable to manipulation of
pages by adversarial webmasters seeking to raise the score
of their sites.
- 7
- See Section 6 for an
approach we are exploring which reduces the ability for even
malicious ODP editors to affect scores in any non-negligible
way.
- 8
- Alternatively,
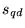 can be used as part of a more general
scoring function.
can be used as part of a more general
scoring function.
- 9
- Several queries which produced very few hits on our repository
were excluded.
- 10
- The URLs within
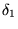 are not ordered with respect to one
another.
are not ordered with respect to one
another.
- 11
- We used 25 iterations of PageRank in all cases.
- 12
- Of course this is a subjective statement; a user study is
presented in Section 4.3.
- 13
- Both the title and URL were presented to the user. The title
was a hyperlink to a current version of the Web page.
- 14
- See for instance http://directory.google.com/Top/Arts/
or http://dir.yahoo.com/Arts/.
- 15
- For instance, estimated class
probabilities for the basis topics.
- 16
- The proof that follows is based on discussions with Glen Jeh (
see [13]).
- 17
- See the end of Section 2 for the description of our
notation.
![]() has a link to page
has a link to page ![]() , then the author of
, then the author of ![]() is implicitly conferring some importance to
page
is implicitly conferring some importance to
page ![]() . Intuitively,
Yahoo! is an important page, reflected by the fact that
many pages point to it. Likewise, pages prominently pointed to from
Yahoo! are themselves probably important. How much
importance does a page
. Intuitively,
Yahoo! is an important page, reflected by the fact that
many pages point to it. Likewise, pages prominently pointed to from
Yahoo! are themselves probably important. How much
importance does a page ![]() confer to its outlinks? Let
confer to its outlinks? Let ![]() be the outdegree of page
be the outdegree of page
![]() , and let
, and let ![]() represent the importance
(i.e., PageRank) of page
represent the importance
(i.e., PageRank) of page ![]() . Then the link
. Then the link ![]() confers
confers
![]() units
of rank to
units
of rank to ![]() .
This simple idea leads to the following fixpoint computation that
yields the rank vector
.
This simple idea leads to the following fixpoint computation that
yields the rank vector
![]() over all
of the pages on the Web. If
over all
of the pages on the Web. If ![]() is the number of pages, assign all pages the
initial value
is the number of pages, assign all pages the
initial value ![]() .
Let
.
Let ![]() represent the set
of pages pointing to
represent the set
of pages pointing to ![]() . In
each iteration, propagate the ranks as follows:2
. In
each iteration, propagate the ranks as follows:2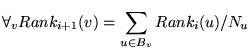
![]() be the square, stochastic
matrix corresponding to the directed graph
be the square, stochastic
matrix corresponding to the directed graph ![]() of the Web, assuming all nodes in
of the Web, assuming all nodes in ![]() have at least one outgoing
edge. If there is a link from page
have at least one outgoing
edge. If there is a link from page ![]() to page
to page ![]() , then let the matrix entry
, then let the matrix entry ![]() have the value
have the value ![]() . Let all other entries
have the value 0. One iteration of the
previous fixpoint computation corresponds to the matrix-vector
multiplication
. Let all other entries
have the value 0. One iteration of the
previous fixpoint computation corresponds to the matrix-vector
multiplication
![]() .
Repeatedly multiplying
.
Repeatedly multiplying
![]() by
by ![]() yields the dominant
eigenvector
yields the dominant
eigenvector
![]() of the
matrix
of the
matrix ![]() . In
other words,
. In
other words,
![]() is the
solution to
is the
solution to![]() is
irreducible (i.e.,
is
irreducible (i.e., ![]() is
strongly connected) and aperiodic [15]. The latter is guaranteed in
practice for the Web, while the former is true if we add a damping
factor
is
strongly connected) and aperiodic [15]. The latter is guaranteed in
practice for the Web, while the former is true if we add a damping
factor ![]() to the rank propagation. We can define
a new matrix
to the rank propagation. We can define
a new matrix ![]() in
which we add transition edges of probability
in
which we add transition edges of probability
![]() between every pair of nodes in
between every pair of nodes in ![]() :
:![]() is given by
is given by
![]() . We will
refer to the solution
. We will
refer to the solution
![]() of
Equation 5, with
of
Equation 5, with
![]() and
a particular
and
a particular
![]() ,
as
,
as
![]() . By appropriately
selecting
. By appropriately
selecting ![]() , the rank vector can be made to prefer
certain categories of pages. The bias factor
, the rank vector can be made to prefer
certain categories of pages. The bias factor ![]() specifies the degree to
which the computation is biased towards
specifies the degree to
which the computation is biased towards ![]() .
.![]() described in Section 2, we use the URLs present in the
various categories in the ODP. We create 16 different biased
PageRank vectors by using the URLs present below each of the 16 top
level categories of the ODP as the personalization vectors. In
particular, let
described in Section 2, we use the URLs present in the
various categories in the ODP. We create 16 different biased
PageRank vectors by using the URLs present below each of the 16 top
level categories of the ODP as the personalization vectors. In
particular, let ![]() be
the set of URLs in the ODP category
be
the set of URLs in the ODP category ![]() . Then when computing the PageRank vector for
topic
. Then when computing the PageRank vector for
topic ![]() , in place of the
uniform damping vector
, in place of the
uniform damping vector
![]() , we use the
nonuniform vector
, we use the
nonuniform vector
![]() where
where![]() consisting of the
terms in the documents below each of the 16 top level categories.
consisting of the
terms in the documents below each of the 16 top level categories.
![]() simply gives
the total number of occurrences of term
simply gives
the total number of occurrences of term ![]() in documents listed below class
in documents listed below class ![]() of the ODP.
of the ODP.![]() , let
, let
![]() be the context of
be the context of
![]() . In other words, if
the query was issued by highlighting the term
. In other words, if
the query was issued by highlighting the term ![]() in some Web page
in some Web page ![]() , then
, then ![]() consists of the terms in
consists of the terms in ![]() . For ordinary queries not done
in context, let
. For ordinary queries not done
in context, let ![]() . Using a unigram language model, with parameters
set to their maximum-likelihood estimates, we compute
the class probabilities for
each of the 16 top level ODP classes, conditioned on
. Using a unigram language model, with parameters
set to their maximum-likelihood estimates, we compute
the class probabilities for
each of the 16 top level ODP classes, conditioned on ![]() . Let
. Let ![]() be the
be the ![]() th term in the query (or query context)
th term in the query (or query context) ![]() . Then given the query
. Then given the query ![]() , we compute for each
, we compute for each ![]() the following:
the following: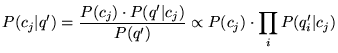
![]() is
easily computed from the class term-vector
is
easily computed from the class term-vector ![]() . The quantity
. The quantity ![]() is not as straightforward. We chose to
make it uniform, although we could personalize the query results
for different users by varying this distribution. In other
words, for some user
is not as straightforward. We chose to
make it uniform, although we could personalize the query results
for different users by varying this distribution. In other
words, for some user ![]() , we
can use a prior distribution
, we
can use a prior distribution ![]() that reflects the interests of user
that reflects the interests of user
![]() . This method
provides an alternative framework for user-based personalization,
rather than directly varying the damping vector
. This method
provides an alternative framework for user-based personalization,
rather than directly varying the damping vector ![]() as had been suggested
in [7,6].
as had been suggested
in [7,6].![]() . Finally, we compute the
query-sensitive importance score of each of these retrieved URLs as
follows. Let
. Finally, we compute the
query-sensitive importance score of each of these retrieved URLs as
follows. Let ![]() be the rank of document
be the rank of document ![]() given by the rank vector
given by the rank vector
![]() (i.e., the rank
vector for topic
(i.e., the rank
vector for topic ![]() ).
For the Web document
).
For the Web document ![]() , we
compute the query-sensitive importance score
, we
compute the query-sensitive importance score ![]() as follows.
as follows.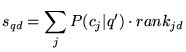
![]() be the coefficient used to
weight the
be the coefficient used to
weight the ![]() th
rank vector, with
th
rank vector, with
![]() (e.g., let
(e.g., let
![]() ). Then note that the
equality
). Then note that the
equality![$\displaystyle \sum_j [w_j \vec{PR}(\alpha, \vec{v_j})] = \vec{PR}\bigl(\alpha, \sum_j [w_j \vec{v_j}]\bigr)$](../../CDROM/refereed/127/img123.png)
![]() . In Section 4.3, we present results of a user
study showing the retrieval performance of ordinary PageRank versus
topic-sensitive PageRank. Finally, in Section 4.4, we provide an initial look at how
the use of query context can be used in conjunction with
topic-sensitive PageRank.
. In Section 4.3, we present results of a user
study showing the retrieval performance of ordinary PageRank versus
topic-sensitive PageRank. Finally, in Section 4.4, we provide an initial look at how
the use of query context can be used in conjunction with
topic-sensitive PageRank.![]() , indicates the degree of
overlap between the top
, indicates the degree of
overlap between the top ![]() URLs of two rankings,
URLs of two rankings, ![]() and
and ![]() . We define the overlap of two sets
. We define the overlap of two sets ![]() and
and ![]() (each of size
(each of size ![]() ) to be
) to be
![]() . In our
comparisons we will use
. In our
comparisons we will use ![]() . The overlap measure
. The overlap measure ![]() gives an incomplete
picture of the similarity of two rankings, as it does not indicate
the degree to which the relative orderings of the top
gives an incomplete
picture of the similarity of two rankings, as it does not indicate
the degree to which the relative orderings of the top ![]() URLs of two rankings are in
agreement. Therefore, we also use a variant of the Kendall's
URLs of two rankings are in
agreement. Therefore, we also use a variant of the Kendall's ![]() distance measure.
See [9] for a discussion of
various distance measures for ranked lists in the context of Web
search results. For consistency with
distance measure.
See [9] for a discussion of
various distance measures for ranked lists in the context of Web
search results. For consistency with ![]() , we will present our definition as a
similarity (as opposed to distance) measure, so that values closer
to 1 indicate closer agreement. Consider two partially ordered
lists of URLs,
, we will present our definition as a
similarity (as opposed to distance) measure, so that values closer
to 1 indicate closer agreement. Consider two partially ordered
lists of URLs, ![]() and
and ![]() , each of length
, each of length ![]() . Let
. Let ![]() be the union of the URLs in
be the union of the URLs in ![]() and
and ![]() . If
. If ![]() is
is
![]() , then let
, then let
![]() be the
extension of
be the
extension of ![]() , where
, where ![]() contains
contains ![]() appearing after all the URLs in
appearing after all the URLs in ![]() .10We extend
.10We extend ![]() analogously to yield
analogously to yield ![]() . We define our
similarity measure
. We define our
similarity measure ![]() as follows:
as follows: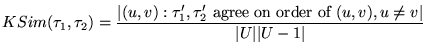
![]() is the probability that
is the probability that ![]() and
and ![]() agree on the relative ordering of a
randomly selected pair of distinct nodes
agree on the relative ordering of a
randomly selected pair of distinct nodes
![]() .
.![]() , discussed in Section 2, affects the degree to which the
resultant vector is biased towards the topic vector used for
, discussed in Section 2, affects the degree to which the
resultant vector is biased towards the topic vector used for ![]() . Consider the extreme
cases. For
. Consider the extreme
cases. For ![]() , the URLs in the bias set
, the URLs in the bias set ![]() will be assigned the score
will be assigned the score
![]() , and all other URLs
receive the score 0. Conversely, as
, and all other URLs
receive the score 0. Conversely, as ![]() tends to 0, the content of
tends to 0, the content of ![]() becomes irrelevant to the
final score assignment.
becomes irrelevant to the
final score assignment.![]() heuristically, after inspecting the rankings for several of the
queries listed in Table 1. We did not concentrate on
optimizing
heuristically, after inspecting the rankings for several of the
queries listed in Table 1. We did not concentrate on
optimizing ![]() , as we discovered that the induced
rankings of query results are not very sensitive to the choice of
, as we discovered that the induced
rankings of query results are not very sensitive to the choice of
![]() . For
instance, for
. For
instance, for
![]() and
and
![]() , we
measured the average similarity of the induced rankings across our
set of test queries, for each of our PageRank vectors.11 The results are given in
Table 2. We see that the
average overlap between the top 20 results for the two values of
, we
measured the average similarity of the induced rankings across our
set of test queries, for each of our PageRank vectors.11 The results are given in
Table 2. We see that the
average overlap between the top 20 results for the two values of
![]() is very high.
Furthermore, the high values for
is very high.
Furthermore, the high values for ![]() indicate high overlap as well agreement (on
average) on the relative ordering of these top 20 URLs for the two
values of
indicate high overlap as well agreement (on
average) on the relative ordering of these top 20 URLs for the two
values of ![]() . All subsequent experiments use
. All subsequent experiments use
![]() .
.![]() . We computed the average, across our test
queries, of the pairwise similarity between the rankings induced by
the different topically-biased vectors. The 5 most similar pairs,
according to our
. We computed the average, across our test
queries, of the pairwise similarity between the rankings induced by
the different topically-biased vectors. The 5 most similar pairs,
according to our ![]() measure, are given in Table 3, showing that even the most
similar topically-biased rankings have little overlap.
Table 4 shows that the
pairwise similarities of the rankings induced by the other ranking
vectors are close to 0. Having established that the
topically-biased PageRank vectors each rank the results
substantially differently, we proceed to investigate which of these
rankings is ``best'' for specific queries.
measure, are given in Table 3, showing that even the most
similar topically-biased rankings have little overlap.
Table 4 shows that the
pairwise similarities of the rankings induced by the other ranking
vectors are close to 0. Having established that the
topically-biased PageRank vectors each rank the results
substantially differently, we proceed to investigate which of these
rankings is ``best'' for specific queries.![]() as discussed in
Section 3.3 yielded
intuitive results for determining which topics are most closely
associated with a query. In particular, for most of the test
queries, the ODP categories with the highest values for
as discussed in
Section 3.3 yielded
intuitive results for determining which topics are most closely
associated with a query. In particular, for most of the test
queries, the ODP categories with the highest values for ![]() are intuitively
the most relevant categories for the query. In Table 6, we list for each test query, the
3 categories with the highest values for
are intuitively
the most relevant categories for the query. In Table 6, we list for each test query, the
3 categories with the highest values for ![]() . When computing the composite
. When computing the composite
![]() score in our
experiments, we chose to use the weighted sum of only the rank
vectors associated with the three topics with the highest values
for
score in our
experiments, we chose to use the weighted sum of only the rank
vectors associated with the three topics with the highest values
for ![]() ,
rather than all of the topics. Based on the data in Table 6, we saw no need to include the
scores from the topic vectors with lower associated values for
,
rather than all of the topics. Based on the data in Table 6, we saw no need to include the
scores from the topic vectors with lower associated values for
![]() .
.![]() score.13The volunteer was asked to select
all URLs which were ``relevant'' to the query, in their opinion.
Furthermore, they were asked to say which of the two rankings was
``better'' overall, in their opinion. They were not told anything
about how either of the rankings was generated. The rankings
induced by the topic-sensitive PageRank score
score.13The volunteer was asked to select
all URLs which were ``relevant'' to the query, in their opinion.
Furthermore, they were asked to say which of the two rankings was
``better'' overall, in their opinion. They were not told anything
about how either of the rankings was generated. The rankings
induced by the topic-sensitive PageRank score ![]() were significantly
preferred by our test group. Let a URL be considered
relevant if at least 3 of the 5 volunteers selected it as
relevant for the query. The precision then is the fraction
of the top 10 URLs that are deemed relevant. The precision
of the two ranking techniques for each test query is shown in
Figure 1. The average
precision for the rankings induced by the topic-sensitive PageRank
scores is substantially higher than that of the unbiased PageRank
scores. Furthermore, as shown in Table 7, for nearly all queries, a
majority of the users preferred the rankings induced by the
topic-sensitive PageRank scores. These results suggest that the
effectiveness of a query-result scoring function can be improved by
the use of a topic-sensitive PageRank scheme in place of a generic
PageRank scheme.
were significantly
preferred by our test group. Let a URL be considered
relevant if at least 3 of the 5 volunteers selected it as
relevant for the query. The precision then is the fraction
of the top 10 URLs that are deemed relevant. The precision
of the two ranking techniques for each test query is shown in
Figure 1. The average
precision for the rankings induced by the topic-sensitive PageRank
scores is substantially higher than that of the unbiased PageRank
scores. Furthermore, as shown in Table 7, for nearly all queries, a
majority of the users preferred the rankings induced by the
topic-sensitive PageRank scores. These results suggest that the
effectiveness of a query-result scoring function can be improved by
the use of a topic-sensitive PageRank scheme in place of a generic
PageRank scheme.
![]() as described in Section 3.3, using for
as described in Section 3.3, using for ![]() the terms of the entire
page, rather than just the term ``blues.'' For the first page
(discussing music),
the terms of the entire
page, rather than just the term ``blues.'' For the first page
(discussing music),
![]() is
ARTS, and for the second page (discussing
depression),
is
ARTS, and for the second page (discussing
depression),
![]() is
HEALTH. The next step is to use a text index to
fetch a list of URLs for all documents containing the term
``blues'' -- the highlighted term for which the query was issued.
Finally, the URLs are ranked using the appropriate ranking vector
that was selected using the
is
HEALTH. The next step is to use a text index to
fetch a list of URLs for all documents containing the term
``blues'' -- the highlighted term for which the query was issued.
Finally, the URLs are ranked using the appropriate ranking vector
that was selected using the ![]() values (i.e., either
ARTS or HEALTH). Table 9 shows the top 5 URLs for
the query ``blues'' using the topic-sensitive PageRank vectors for
ARTS, HEALTH, and
NOBIAS. We see that as desired, most
of the results ranked using the ARTS-biased vector
are pages discussing music, while all of the top results ranked
using the HEALTH-biased vector discuss depression.
The context of the query allows the system to pick the appropriate
topic-sensitive ranking vector, and yields search results
reflecting the appropriate sense of the search term.
values (i.e., either
ARTS or HEALTH). Table 9 shows the top 5 URLs for
the query ``blues'' using the topic-sensitive PageRank vectors for
ARTS, HEALTH, and
NOBIAS. We see that as desired, most
of the results ranked using the ARTS-biased vector
are pages discussing music, while all of the top results ranked
using the HEALTH-biased vector discuss depression.
The context of the query allows the system to pick the appropriate
topic-sensitive ranking vector, and yields search results
reflecting the appropriate sense of the search term.![]() , based on how closely the user's
context accords with each of the basis topics.
, based on how closely the user's
context accords with each of the basis topics.![]() used to create the topic-sensitive rank
vectors. This approach has the potential of being more resistant to
adversarial ODP editors. Currently, as described in Section 3.2, we set the damping vector
used to create the topic-sensitive rank
vectors. This approach has the potential of being more resistant to
adversarial ODP editors. Currently, as described in Section 3.2, we set the damping vector
![]() for topic
for topic
![]() to
to ![]() , where
, where ![]() is defined in
Equation 6. In the modified
approach, we instead first train a classifier for the basis set of
topics using the ODP data as our training set, and then assign to
all pages on the Web a distribution of topic weights.15Let this topic weight of a page
is defined in
Equation 6. In the modified
approach, we instead first train a classifier for the basis set of
topics using the ODP data as our training set, and then assign to
all pages on the Web a distribution of topic weights.15Let this topic weight of a page
![]() for category
for category ![]() be
be ![]() . Then we replace Equation 6 with
. Then we replace Equation 6 with![]() for some fixed
for some fixed
![]() .17 For brevity let
.17 For brevity let
![]() .
Furthermore let
.
Furthermore let
![]() , and
, and
![]() . We claim that
. We claim that
![]() . In other
words,
. In other
words, ![]() is itself a PageRank vector, where the
personalization vector
is itself a PageRank vector, where the
personalization vector ![]() is set to
is set to ![]() . The proof follows.
. The proof follows.![]() satisfies Equation 5 (with
satisfies Equation 5 (with
![]() ), we have that
), we have that![$\displaystyle \equiv \sum_j [w_j \vec{r_j}]$](../../CDROM/refereed/127/img234.png)
![$\displaystyle = \sum_j [w_j ((1-\alpha) M \vec{r_j} + \alpha \vec{v_j})]$](../../CDROM/refereed/127/img235.png)
![$\displaystyle = \sum_j [(1-\alpha) w_j M \vec{r_j}] + \sum_j [\alpha w_j \vec{v_j}]$](../../CDROM/refereed/127/img236.png)
![$\displaystyle = (1-\alpha) M \sum_j [w_j \vec{r_j}] + \alpha \sum_j [w_j \vec{v_j}]$](../../CDROM/refereed/127/img237.png)
![]() satisfies Equation 5 for the personalization vector
satisfies Equation 5 for the personalization vector
![]() ,
and our proof is complete.
,
and our proof is complete.