Copyright is held by the author/owner(s).
WWW2002, May 7-11, 2002, Honolulu, Hawaii, USA.
ACM 1-58113-449-5/02/0005.
Communities are catching social attentions because the decision of a human relies on information available in one's belonging group of people [1, 2, 3]. This trend existed from a long time ago, as long as the history of human culture. Meetings for group-wise decision making and conversations with coworkers have been the information source for each participant. The recent outbreak of community-wares comes from the growth of the variety of powerful communities such as enterprise decision teams, customer groups etc., hand in hand with the growth of communities on the Internet, e.g., mailing lists, message boards, and chat rooms. These trends made various community-based human activities for people with various value criteria.
As a result, various ranges of Web communities appeared - match (friends or mail-pals) making, collaboration, etc. We can classify them into various types of communities for various aims. In one of match-making type, frictions have been caused in the real world by partners who came to know each other in the virtual world, i.e., the Internet. On the other hand, in a problem solving community, the content flow rather than the participants' characters are the main focus of attentions for most participants. The latter type may enable the creation of useful knowledge, rather than new human relations. However, in a problem solving community, new comers may feel hard to take part in the communication because the discussions are highly specialized and the value criteria shared are strongly biased, so people with average knowledge seem to be excluded. This sometimes disturbs the growth of community. Between these two extreme types, chats about easy topics allowing the entry of people with various values exist, where the excitement is remarkable but collisions due to gaps between value criteria can lead to flaming and the disorder of topics.
Thus, the aims and problems underlying each type of community have great impact onto business issues, e.g., whether the community creates useful knowledge, how easy it is to join the community, or why the community is good for making advertisement for commerce [4]. In this paper, we analyze the text of communication in message boards, which we take as an example of Web communities. The types of communities in existing classification as in [4] are generalized systematically, by featuring each type of community on three dimensions we introduced. These dimensions correspond to topological features of the output graph of KeyGraph [5], a co-occurrence graph of words and word-clusters for textual information.
The classification of communities in [4] is being accepted as a model of Web-based societies as business target. Because the book is in Japanese, let us show its classification of Web communities as follows.
Communities of type A and B are hard to distinguish. For example, discussants in a community talking about ecological issues are concerned with how to solve problems in the ecology. This type looks like both A and B. For making the borderline clear, we revise A and B to the following categorization.
A': Centralized arguments for solving a problem
B': Centralized arguments for solving sub-problems relevant to a given problem
In A', the discussion goes lead by predefined organizer(s). On the other hand, participants begin to communicate for solving relevant problems in a decentralized manner in B', and ideas coming out from local communications in parts of the community are compared, selected, or connected by cooperative arguments. Leaders here appear in the course of nature, who have knowledge of higher quality than other participants or who talks more than others. As a result, both A' and B' types of community have some person or topic in the center. Similarly, C and D, specialized to product/service consumers, can be generalized to C' and D' from the aspect of communication content as:
C': Decentralized solving of sub-problems relevant to a given problem
D': Weakly centralized (distributed) solving of sub-problems relevant to a given problem
A community of type E is directed even weaker to defined or concrete topics, and can be pus as:
E': Free conversations for making and sharing a community without defined topics
In F, the communication makes progress in various directions in each community of a shared area of interest, rather than to an absolutely good solution of a shared problem. In this sense, F can be distinguished from communities above, to be described as:
F': Weakly centralized communications on freely selected topics under a shared context, where topics are not always for problem solving but may include experiences with wine-tastes.
The discussion above leads to the classification of communities on the u,v, and w as follows.
Introducing these attributes, we can put the community classes A' through F' above as follows.
This classification implies the existence of other types of communities because we should have 27 (3*3*3) types. In the case of (u, v, w) = (0,1,0), e.g., ones in the poor-mannered community site, the communication spreading to various contexts by anonymous participants leads not to decisions, but to quarreling with words as ``die" ``stupid" etc.
In this paper, we propose a method to compute u, v andw, given a community message board and its text of messages and message writers. Realizing this method, we can guess what sense a community with seemingly complex communications is making and anticipate what sense it will make. For example, if we obtain (u, v, w) = (2,1,1), we can guess there is an expert leading the community to solve problems in a certain domain, as in a community of type B' or B above. This leader can be considered a good teacher for ones interested in the domain. On the other hand, if we obtain (u, v, w) = (1,1,0), we can guess the community is a club-like gathering and can join without hesitation. Further, if the community is creating useful knowledge, the communication content can be a textbook for business.
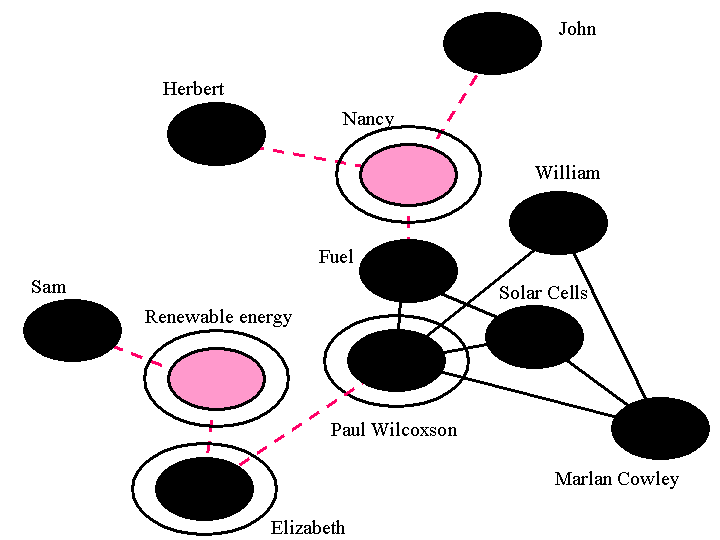
We compute u, v and w based on the thread-based co-occurrence of words in a message board. If there is a message M not a response to a previous message and there are responses to M, those responses and M are called a thread as a set. If a pair of words co-occurs frequently in the same thread, we regard the pair as of high co-occurrence. For example, Figure 1 is a part of a message board talking about ecological issues. The part in Figure 1 focuses attention onto how to make a hybrid car - known as gentle to the atmosphere - prevalent. A group of participants who frequently co-occur in the same threads can be regarded as sharing the (at least temporary) context of interest.
Suppose there are two or more such groups of participants. A participant who stays in one group can be regarded as concentrated in a narrow specific context. On the other hand, one talking to many groups can play a significant role as a messenger helping those groups exchange information and consider new topics, or sending commands to multiple sections, although she may otherwise have just an unstable interest drifting among groups. In either case, she has a potential to develop her ideas to prevail to a wide part of the community, which may lead to innovating ideas. Generally, a leader can be:
These people are followed by people in each local group or sub-community [1]. People who only organize or manage a community, e.g., an administrator of a mailing list, is not usually called a leader because such one does not show directions of communication. However, if this organizer gives new topics to talk about, he can be seen as a leader or:
That is, a leader is a participant from whom the community comes to grow in a radiating manner. In a centralized Web community, such a member catches attentions of other members, more strongly than mutual attentions between non-leader members. The stronger the centralization, the more the communication between the leader and others overwhelm distributed (among non-leaders) communication. As a result, the value of u in Section 3 can be expressed by the extent the community forms a one-to-many radiation structure.
On the other hand, a community where new ideas and leaders often occur has multiple groups among which information is exchanged directly via weak ties and stimulates changes [6,7], rather than centralization. New ideas are sometimes imported to a certain group X from other groups, and people in X can create new knowledge by talking on the new information. As pointed in [8], new idea-combinations trigger innovations.
In order to catch the characteristics of community types, we construct a graph representing human-human and topic-human relations based on the text in message boards. From the discussion above, this graph is desired to satisfy the following conditions:
As a graph satisfying both conditions, we apply KeyGraph [5]. In KeyGraph, the input data D of a1, a2, ... occurring sequentially is dealt in the form as:
D = a1, a2, .... an. b1, b2, b3 ..., bm. c1, c2, .... cp ...
We call each datum ``a1", ``a2", ....or ``cp" a word, and the sequence between two nearest periods a sentence. Accordingly, D is called a document. The algorithm of KeyGraph is summarized as follows, with the metaphor of building (make basis, columns, and then the roofs)
The Process of KeyGraph [5]
In the case of Figure 1, by assigning each participant name or each word in communication to a word and each thread to a sentence in KeyGraph, we obtain the following document from the communication history.
The result of KeyGraph is as in Figure 2, where the lower part corresponds to the part of communication shown in Figure 1. Generally, a roof comes to be of low frequency but a significant position in the graph. In a community, sticks in clusters mean strong ties between people, whereas roofs and columns can be a messenger connecting multiple groups or an innovator touching various participants, and words realizing weak ties between clusters [6,7]. Nodes and sticks in basic clusters were shown in black and columns and roofs were in red in KeyGraph, but let us focus attention to the topological structure of each graph if the paper is printed in black and white.

Based on the output graph of KeyGraph, let us first consider u, the strength of centralization of a community: That is, the extent the graph looks like few-to-many radiation means the strength of leader if the few nodes represent participant-names, and the leading topic if the few nodes represent words in the communication. A straight-forward expression for a centralized community might be
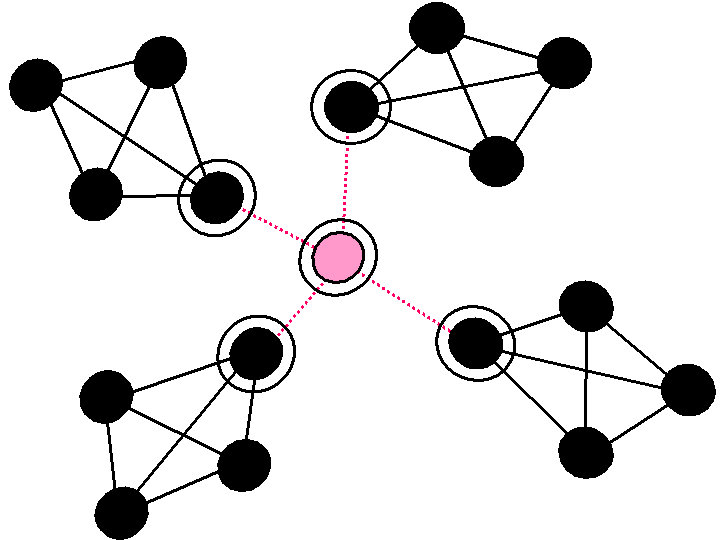
u0 = 2 Maxi outi / N * avri(outi). (1)Here, N and outi represent the number of all nodes in the graph and the number of edges touching each node i, respectively. If the graph is totally centralized, i.e., there is one central node and all other nodes not connected to each other but are connected to the central node, then Maxi (outi) is equal to N-1 and other nodes have only one touching edge (i.e., outi =N -1 if i is the central node and outi =1 otherwise). In this case, accordingly, u0 takes the value of 1. If the central node x has a smaller value of outx and other nodes are connected to each other, u0 becomes smaller. Yet, Eq.(1) is not complete for expressing a community of type A'. For example, Figure 3 has a clearly central node connected to all clusters. However, each node y adjacent to the central node has nearly the equal value of outy to Maxi (outi) i.e., 4. In this case u0 is near to 2/N, much smaller than 1.
A function more appropriate for expressing the degree of centralization is thus desired. A small world has been introduced as a typical form of community in the nature, e.g.,a group of creatures, human, and Web pages [9,10,11]. The extent to which a community looks like a small world, i.e., small-worldliness S, is defined as:
S= C / L. (2)
A community of large S is called a small world. Here, C is the relative density of graph G, defined as the average rate of edges existing among nodes surrounding each node in G, (this rate is 2/3 for ``Solar Cells" in Figure 2, because the number of edges connecting ``Fuel" ``Paul Wilcoson" and ``Marlan Cowley" surrounding ``Solar Cells" is 2, among all 3 possible edges). L is the average value of the shortest distance from each node in G to other nodes in G. Both C and L are normalized with dividing by their values for a random graph of the same number of nodes and edges as G. Differing from [12], here we define the distance between two nodes without a connecting path in G as extremely long - 100 times longer than other nodes.
If human relations in a community are represented by a graph, C means the effect of daily local communications of participants or basic2xf concepts usually talked about. On the other hand, L means the difficulty of information propagation between participants linked via various relations including strong (usual or daily) and weak (unusually communicating) ties [11]. A small world of large S can be regarded as a community where weakly-tied pairs of strongly-tied local sub-communities exchange information to distill new ideas. That is, these variables represent the role of participants and concepts to other participants.
We extend the idea of small world, to formalize u and v as well as creativity w. Here, we introduce Cx and Lx separately for each node x and consider the role of nodes in the overall community. This leads to featuring the community, because the role of each particle, i.e., participant or a concept/idea expressed by words, to the community can be reflected to the role of the community to participants' thoughts and concept developments from communication.
| Large Cx | Small Cx | |
| Large Lx | x is in a peripheral cluster | x is in a central cluster |
| Small Lx | x is far from an ernhanced center | x is in the center not clustered |
Common facts about community formation are shown in Table 1. For example, a leader in a centralized community contacts other members, but those non-leaders do not make communications with each other often. If the non-leader members communicate and co-work to make decisions, we do not call it a centralized community, because the community comes to be a decentralized problem solving system. Thus both Cx and Lx take small values if x represents a leader. On Table 1, we formalize the role of a node in a graph as:
Then, we express the extent of the centralization by p, the coherence of communication context by q, and the application of various information to idea distillation and innovation in local communities by r, of the community represented by the overall graph as in Eq.(6).
Here, Max and avr, respectively, mean the maximum and the average values for all nodes. We can then define the values of u, v and w in Section 2 as in Eq.(7), corresponding to Section 3.
Here, t1 to t6 are the given thresholds for variables. Based on experiences with various communities, we set t1=3.0, t2=1.5, t3=.3, t4=.1, t5=3.0, and t6=1.0 where communities could be classified to A' to F' with the keenest fitting to our impression of exiting Web communications.
In KeyGraph applied to a community as explained above, we can see co-occurrences of (a) participant-participant, (b) participant-word, and (c) word-word. These three types of co-occurrence mean (a) context-sharing group of people, (b) the interest of people in concepts, and (c) hidden context or concept underlying co-occurring set of words. Because the contexts, interests and concepts maybe hidden, i.e., do not appear explicitly in communications, let us look at the output figures of KeyGraph, and make numeric evaluations of the implication of each output.
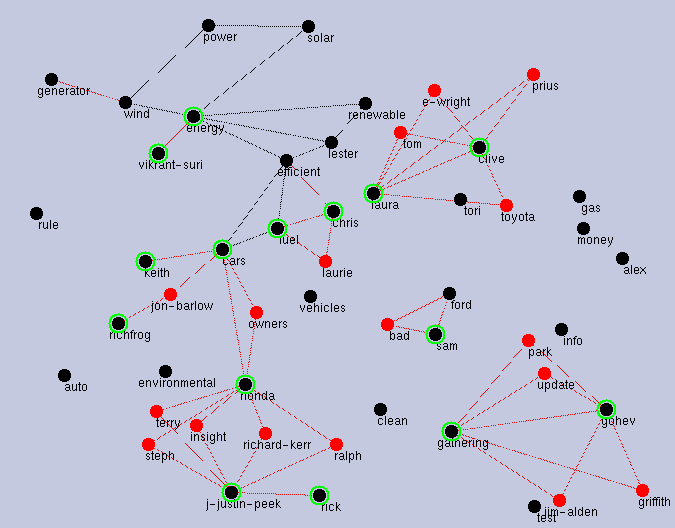
Figure 4 shows the result of KeyGraph for a community talking about energy-saving methods, in a community-collection site of ecology. Many opinions here are concentrated in the recent popular topic ``hybrid cars." The value of u is 1 reflecting ``Honda" as a (not strongly) leading topic, so we can see not a human leader but a leading topic organizing some part of the community. The graph is scattered to connected sub-graphs, and the value of v is 0. This means the community is of low consistency of context, e.g. aiming at solving multiple problems. w is 1, meaning the community is somehow dedicated to creative decisions relevant to hybrid cars. (u, v, w)=(1,0,1) does not correspond to any of A' to F' defined in Section 3. In fact, few new ideas were observed to come out of this community - they exchanged existing experiences and knowledge.
However, if we take a part of the graph, we can find features of creative solving of coherent problems: The left-hand cluster of Figure 4 shows a structure in the order of ``car brand (Honda) -> first order functions (fuel, efficiency) -> second order functions (solar, wind)." Here, the first order functions are functions of which average car users are aware, whereas the second order functions are recognized by car users with advanced consciousness of ecology. This connected graph, representing the relations between interests in these functions, have been formed by the communications of these different users. Thus, the left-hand side cluster has multiple contexts relevant to each other, relevant to car functions. If you trace the communication including words ``Honda" ``solar power" etc., in the order of node-connection, you will understand the meaning of second-order functions with smooth shifts from familiar (beginner's) to unfamiliar (advanced) contexts. This cluster takes (1,1,1) as the values of (u, v, w) supporting the fact this community is of type D', i.e., weakly centralized (around cars from Honda) for solving sub-problems relevant to a share problem (introduction of solar and hybrid cards to roads).
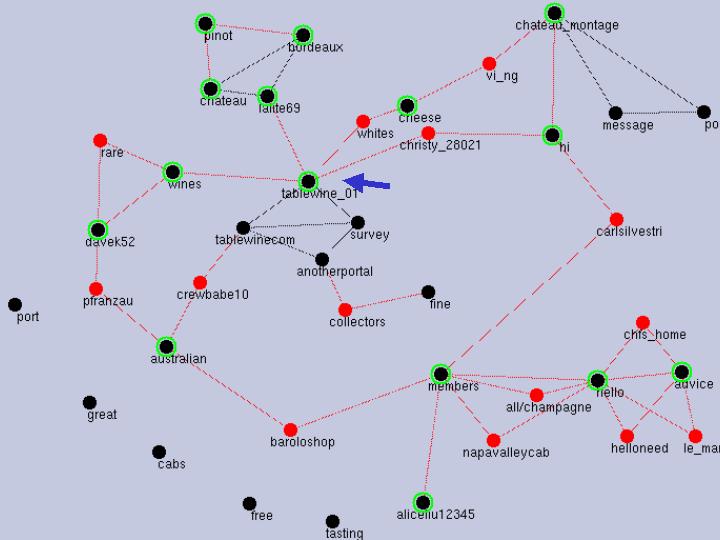
Web communities about wine came to be developed in various directions, and here we deal with one where users organize the message board for themselves. Figure 5 shows the result of KeyGraph for a community of wine collectors. The participants have specific knowledge about wine, and there is no sommelier much more particular about wine than other participants. Thus the community is decentralized by nature, although it has some participants with strong opinions as ``tablewine_01'', arrowed in the upper half of the graph. In this weakly centralized community with some local clusters (representing local communications) linked to each other as in a small world, participants discover new interests. (u, v, w) is (1, 1, 2) in this case, to form type F' i.e., weakly centralized communications on freely selected topics in a shared context. This result matches with the fact people feel they are making a club here. In fact, this is a site called a club on the Web where participants sometimes create knowledge or serve others with new satisfactory information about wine bottles to collect.
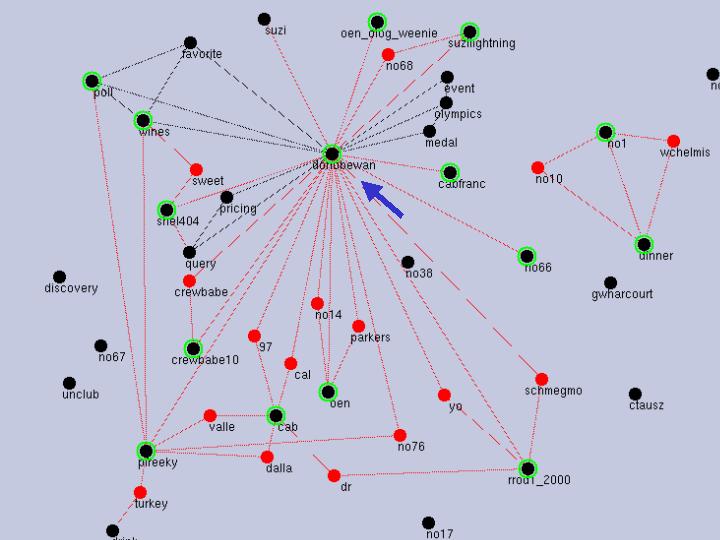
In another wine community as in Figure 6, a sommelier (``donobewan'' of the thick arrow) puts a quiz onto the board almost every week, and participants' communications are accelerated by their trial to answer those questions. The sommelier also answers participants' questions. This is a highly centralized community whose most remarkable feature is the large value of u, i.e., (u, v, w) =(2,1,1). Although this is a site called a wine club, the strong organizer is managing the communications here - as in a group where participants talk for solving various sharable problems. That is, this community is of type B' as the value of (u, v, w) above means.
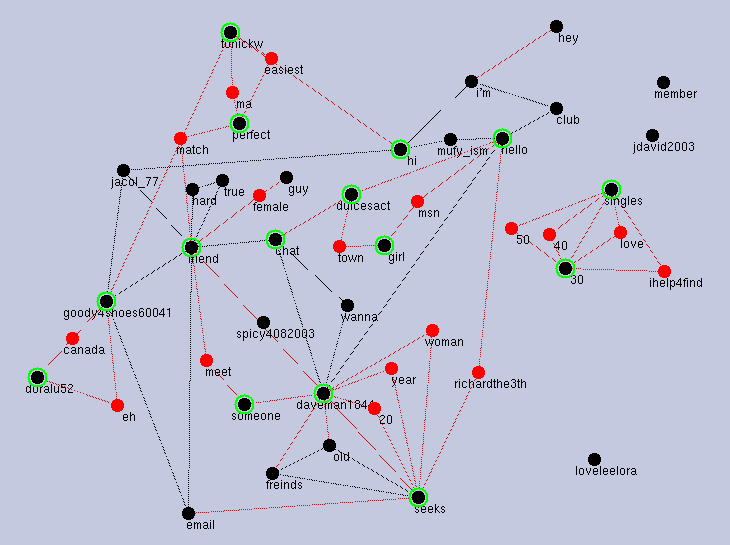
In Figure 7 is the result for a match-making (finding friends, e-mail pals, etc.) community. The value of (u, v, w) was obtained as (0,1,0) which can be seen as a mixture of C' (decentralized solving of sub-problems relevant to a given problem) and E' (free conversations for sharing a community without defined topics). This corresponds to the facts in the community. For example, one first gives a message as ``does any one want a e-mail pal ?" and this problem is solved locally, i.e., by very small number of people in the community. Yet the problems range across too wide topics to be shared in the whole community, and their solutions were not creative at all.
| Predicted u, v, w in Section 3 | Results of u,v, w: x (y) means x=average and
y=2sigma, where sigma =standard deviation |
|
| A' | 2, 2, 2 | 1.7 (.3), 1.8 (.2), 1.6 (.3) |
| B' | 2, 1, 1 | 1.6 (.3), 1.3 (.3), 1.0 (.2) |
| C' | 0, 1, 1 | 0.2 (.3), 0.8 (.3), 1.2 (.1) |
| D' | 1, 1, 1 | 0.2 (.3), 0.8 (.3), 1.2 (.1) |
| E' | 0, 0, 0 to 2 | 0.3 (.3), 0.1 (.2), 0.9 (.4) |
| F' | 1, 1, 0 to 2 | 0.9 (.2), 1.2 (.4), 1.2 (.7) |
In the similar manner to the discussions above, we took ten message boards on the Web for each type as A' through F'. The ``correct" category for each board was given manually by reading the communication contents. Table 2 shows the average values for each type. This result shows the approximate correspondence of obtained results to the prediction of values of (u, v, w) in Section 3. We conclude our three dimensions (u, v, w) form a powerful description of essential features of communities.
We made a three-dimensional space for featuring the essence of communities. This helps in surveying the essence of a community, e.g. whether the community creates useful knowledge, how easy it is to join the community, or whether/why the community is good for making advertisement for commerce. In contrast with previous analysis of human networks on computer mediated communities (CMC) [13], we showed the raw and shallow textual information in communication-sites reflects the dynamics of various communities, across wide types from business aspect.
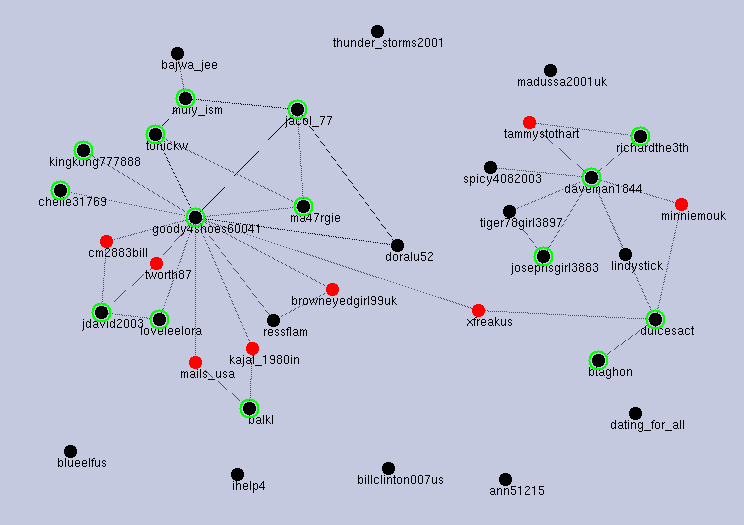
Yet we should be aware of other dimensions. For example, the contents (words and participant names) of communications were seen as C' or E', in Figure 7. However, the graph was much simplified as in Figure 8, if we took only participant names in input D to KeyGraph. The essence of the community seems to be reflected to the results. That is, if the essence is about human relations, human relation structure will be reflected to the result of KeyGraph as in Figure 8. In Figure 8 (u, v, w) took the value-set of (2, 1, 2), well-organized as A' or B'. The difference between Figure 7 and Figure 8 implies there are two relatively strong leaders to make new human relations, but these human relationships do not come from communication topics and topics are just by-products of human relations. In the future work, we aim at formalizing features of communities from various aspects as community topics, human-relations etc., for answering the question ``which community changes the human life?"
1. Rogers, E.M., Diffusion of Innovations, Free Press (1962)
2. Bordia, P. and Rosnow, R.L., Rumor as Group Problem Solving : Development Patterns in Informal Computer-Mediated Groups, Small Group Research, Vol.30 pp.8 - 28. (1999)
3. Nonaka, I., and Takeuchi, H., The Knowledge Creation Company , Oxford University Press (1995)
4. Ishikawa, N., Competitive Advantage Community Strategy, Soft Bank Publishing (2000) In Japanese
5. Ohsawa, Y., et al, KeyGraph: Automatic Indexing by Co-occurrence based on Building Construction Metaphor, Proc. Advanced Digital Library Conference (IEEE ADL'98) pp.12-18 (1998)
6. Granovetter, M.S., The Strength of Weak Tie, The American Journal of Sociology Vol. 78 pp.1360 - 1380 (1973)
7. McPherson, J.M., Popielarz, P.A., and Drobnic, S., Social Networks and Organizational Dynamics. American Sociological Review, Vol.57 pp.153-170 (1992)
8. Goldberg, D.E. The design of innovation: Lessons from genetic algorithms, lessons for the real world. Navigating Complexity, IlliGAL Report 98004 (1998).
9. Watts, D.: Small World: the Dynamics of Networks between Order and Randomness, Princeton (1999)
10. Watts, D. and Strogatz, S. Collective Dynamics of Small World Networks, Nature, 398 (1998)
11. Albert, R., et al, The Diameter of the World Wide Web, Nature, 401 (1999)
12. Matsuo, Y., Ohsawa, Y., and Ishizuka, M., A Document as a Small World, New Frontiers in Artificial Intelligence, LNAI 2253, (Springer Verlag), pp. 444 - 448 (2001)
13. Garton, L., and Wellman, B., Studying On-Line Social Networks, Doing Internet Research, edited by Steve Jones, Thousand Oaks, CA (1999)