In this paper, we aim at finding influential people, comments, and terms contributing the discovery of fascinating topics stimulating peoples' interest. For this purpose, we propose an Influence Diffusion Model (IDM) in text-based communication, where the influence of people, comments, and terms are defined as the degree of text-based relevance of messages. We apply this model to Bulletin Board Service on the Internet, and present our discoveries on experimental evaluations.
Influence Diffusion Model, text-based communication, BBS
Business people, especially marketing researchers, are keen to understand peoples' potential sense of value to create fascinating topics stimulating peoples' interest. In this paper, we focus on new communication places on the Internet such as E-mail, ICQ, Chat, or Bulletin Board Service (BBS). The tools enable us to meet people who are sensitive to the trend and having a great influence on our decision-making. Katz et al. called this type of people as ``opinion leader'' [1].
In this paper, we aim at finding influential people, comments, and terms contributing the discovery of such topics. For this purpose, we propose an Influence Diffusion Model (IDM) in text-based communication, where the influence of people, comments, and terms are defined as the degree of text-based relevance of messages. We apply this model to a BBS, and present our discoveries on experiments.
Diffusion research has been attracted research attentions for decades. [1][2]. Focusing on the diffusion on text-based communication, the researches of computer mediated communications (CMC) are deeply relevant. For example, Kaneko et al. analyzed the comment-chain of e-mails in a mailing-list by using network analysis methods to discover influential comments/people [3]. The study used only the structure of comment-chain, not used the contents.
In this section, we explain our idea of diffusion of influence by focusing on BBS. One of the features of BBS is that communications between people are done by exchanging comments, i.e., posting new comments or replying to the comments. Our first assumption is that the relations of comments, called comment-chain, show the flow of influence. For example, if comment Cy replies to comment Cx, it is considered that Cy is affected by Cx. Similarly, if person Y replies to a comment of person X, Y is considered to be affected by X. In these cases, the influence diffuses from Cx to Cy / from X to Y. In this way, the influence diffuses throughout the comment-chain. Another feature of BBS is that comments are written by natural language composed of terms. Our second assumption is that people's idea is expressed and propagated by the medium of terms. Therefore, the process of diffusion of influence is defined as follow.
Definition 1 In text-based communication, influence diffuses along the comment-chain by medium of terms, i.e., words or phrases.We define the influence by the degree of terms propagating through the comment-chain. For example, If Cy replies to Cx, the influence of Cx onto Cy, ix, y, is defined as
ix, y = | wx ∩ wy | / | wy | ,
where wx and wy are the set of terms in Cx and Cy respectively. In addition, if Cz replies to Cy, the influence of Cx onto Cz via Cy, ix, z, is defined as
ix, z = | wx ∩ wy ∩ wz | / | wz | × ix, y ,
where wz are the terms in Cz. It is considered that the more a comment affects other comments, the more the influence increases. And the same can be applied to the influence of people/term. The influence of a subject (including comment, people or term) then comes to be measurable.
Definition 2 The influence of a subject (a comment, person, or term) to the community is measured by the sum of influence diffused from the subject to all other members of the community.Applying Definition 2 to Cx, the influence (here after, let us skip ``to other members of the community'') is measured by the sum of influence diffused from Cx, i.e., ix, y + ix, z if the community has three members x, y and z.

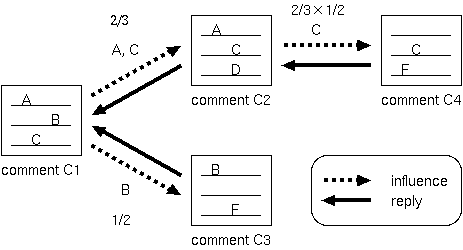
For example, let us measure the influence by using a sample comment-chain illustrated in Fig.1 where C1 is replied to by C2 and C3, and C2 is replied to by C4. In this case, term A, C are propagating from C1 to C2, term B is propagating from C1 to C3, and term C is propagating from C2 to C4. Here, the influence of C1 is calculated as follows.
The inluence of C1 onto C2: The number of propagated terms from C1 to C2 is two (A, C), and the number of terms in C2 is three (A, C, D). Then, the influence from C1 to C2 is 2/3.
The influence of C1 onto C3: The number of propagated terms from C1 to C3 is one (B), and the number of terms in C2 is two (B, F). Then, the influence from C1 to C3 is 1/2.
The influence of C1 onto C4 through C2: The number of propagated terms from C1 to C4 via C2 is one (C), and the number of terms in C2 is two (C, F). Considering that the influence of C1 onto C2 is 2/3, the influence of C1 onto C4 via C2 becomes 2/3 × 1/2 = 1/3.
According to Definition 2, the influence of C1 in Fig.1 is calculated as (the influence from C1 to C2) + (the influence from C1 to C3) + (the influence from C1 to C4) = 2/3 + 1/2 + 1/3 = 3/2. Similarly, the influence of C2, C3 and C4 are calculated as 1/2, 0 and 0 respectively. Therefore, C1 is selected as the most influential comment in Fig.1.
Due to space limitation, we only present our discoveries on experiments and skip the discussions. The comment-chain analyzed here is composed of 17 comments. The main topic is clothing of fleece, especially about popular color and the Internet shopping.
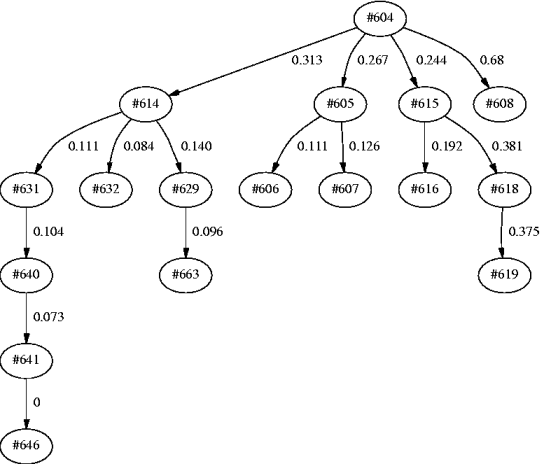
The flows of influence between comments are shown in Fig.2, and the top 5 comments in the order of values of diffusing influence are shown in Table 1.
| Ranking | Comment ID | Influence |
| 1 | #604 | 1.504 |
| 2 | #615 | 0.574 |
| 3 | #618 | 0.375 |
| 4 | #614 | 0.337 |
| 5 | #605 | 0.237 |
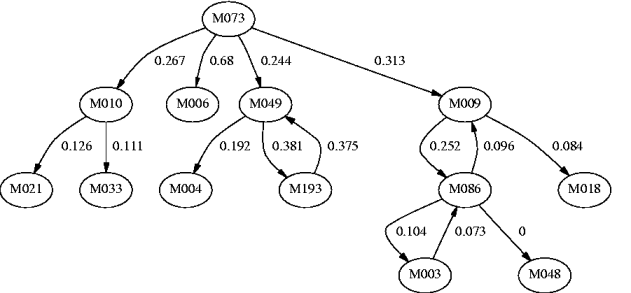
The structure of comment-chain also forms human relations. The influence of a person is defined as the sum of influence of his/her comments. The relations of people, called human network, are shown in Fig.3 and the top 5 people in the order of values of diffusing influence and their comments are listed in Table 2.
| Ranking | Member ID | Comment ID | Influence |
| 1 | M073 | #604 | 1.504 |
| 2 | M049 | #615, #619 | 0.574 |
| 3 | M193 | #618 | 0.375 |
| 4 | M009 | #614, #663 | 0.337 |
| 5 | M010 | #605 | 0.237 |
The influence of comments is propagated by the medium of tems. By assuming that all terms mediate the propagation of equal influence, we can calculate the influence of terms. The top 10 terms in the order of values of diffusing influence are listed in Table 3.
| Ranking | Term | Influence |
| 1 | shop | 0.172 |
| 2 | color | 0.158 |
| 3 | fleece | 0.145 |
| 4 | the Internet | 0.145 |
| 5 | shopping | 0.127 |
| 6 | original | 0.127 |
| 7 | pink | 0.124 |
| 8 | pale olive | 0.099 |
| 9 | poster | 0.061 |
| 10 | UNIQLO | 0.056 |
In this paper, we proposed an Information Diffusion Model (IDM) in text-based communication, and present our discoveries on experiments. The model is one of the formalization of diffusion process that have been attracted attention for decades. In the future work, we plan to apply the model to other archives of text-based communication, such as mailing-list archives, logs of customer support center, and conversation history archives.