In this paper, we propose a new definition of the distance between two pages, called average-clicks. It is based on the probability to click a link through random surfing. We compare the average-clicks measure to the classical measure of clicks, and show that average-clicks fits better to the users' subjective distance.
average-clicks, link structure, random surfer model, subjective distance
There have been a number of recent activities on how to exploit the link structure of the Web. Most of these works analyzing the structure of the Web graph assume the length of each link to be 1 (unit), and the clicks between two pages are counted to measure the distance. However, the distance measured by the number of clicks doesn't reflect well the users' subjective distance. For users, it requires a great effort to find and click a link among a large number of links than a link among a couple of links. If we count minimal clicks to measure the distance between two pages, the path is likely to include link collections, such as Yahoo! directories [1].
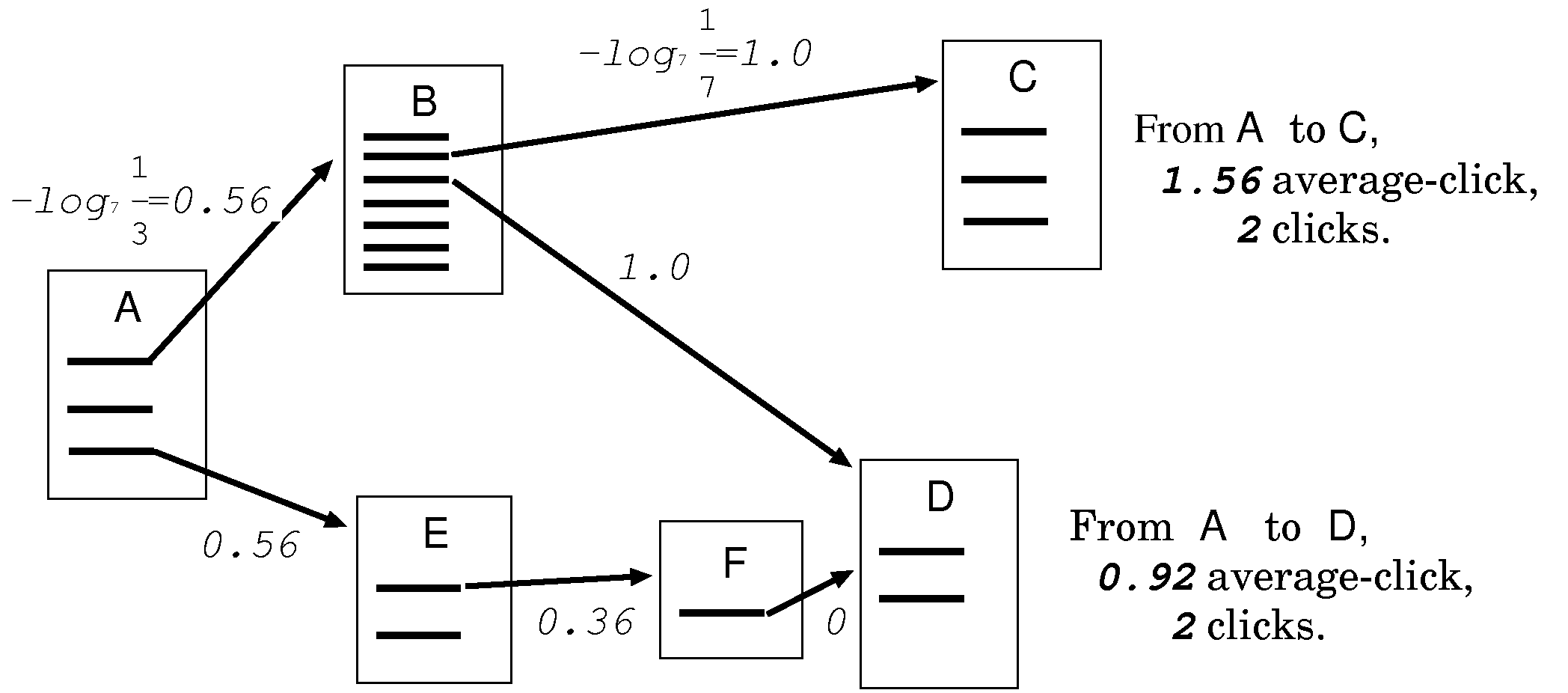
In this paper, we propose a new definition of the distance between two pages, called average-clicks instead of the classical "clicks" measure. This measure reflects how many "average clicks" are needed from a page to another page. An average-click is one click among n links. And two average-clicks is a distance of two successive clicks among n links for each, or one click among n2 links. (We employ n=7.) The average-click is defined on the probability for a "random surfer" to reach the page: A random surfer keeps clicking on successive links at random. The probability for a random surfer in page p to click one of the links in page p is considered as 1/OutDegree(p) in this model. We annotate the link in page p with the length of -logn (1/OutDegree(p)). An average-click is a unit distance of this measure.
By a random surfer model, the probability to click each link in page p is α/OutDegree(p), where α is a damping factor and OutDegree(p) is the number of links page p has. In probability 1-α, a random surfer jumps to a random Web page. Following [2] α is usually set to be 0.85, however, we set α=1 for simplicity.
We annotate a link with the length as negative logarithm of probability, so that summing lengths is akin to multiplying probabilities. A length of a link in page p is defined as
The distance between two pages p and q is defined by the shortest path, that is, the sum of the length of the shortest path from p to q. From a probabilistic point of view, this is equivalent to focus only on the path with the largest probability for a random surfer to get from page p to page q.

Fig. 1 illustrates some pages and the links between them. Page A has three links, thus the length of each link is -log7 (1/3) ≈ 0.56 average-click. As page B has seven links, the length is each 1 average-click. Summing 0.56 and 1, the distance from A to C is 1.56 average-click. In the case of page D, there is two paths from page A to D. The average-clicks is smaller in the lower path, though it takes three clicks. The shortest path in terms of average-clicks is the lower path, while the path with minimal clicks is the upper path.
This model offers a good approximation to our intuitive concept of distance between Web pages. For example, Yahoo! top-page has currently more than 180 links. In our definition, the length from the top-page to each sub-page is far, as the upper path in Fig. 1. On the other hand, the path length by the local relation, such as the link to one's friends or the link to one's interests, is estimated rather short, as in the lower path of the figure. Intuitively we think the path through the Yahoo! top-page is longer than the path along the acquaintance chain with the same clicks. In our model, page C is more distant from page A than page D, and this fits well to our intuition.
We implement the best-first algorithm to search the shortest path from a starting URL to a target URL. This best-first algorithm is similar to the breadth-first algorithm for clicks measure.
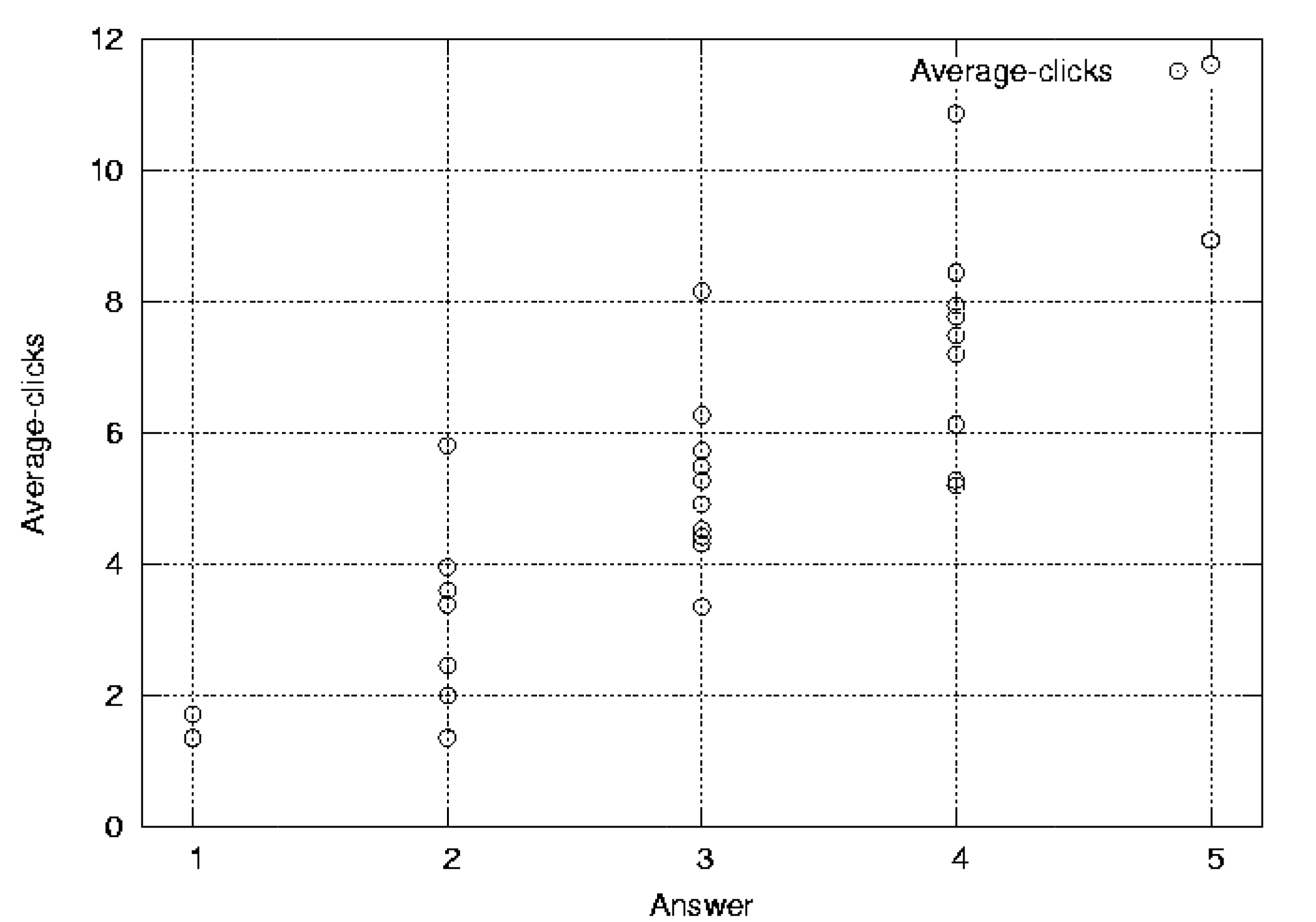
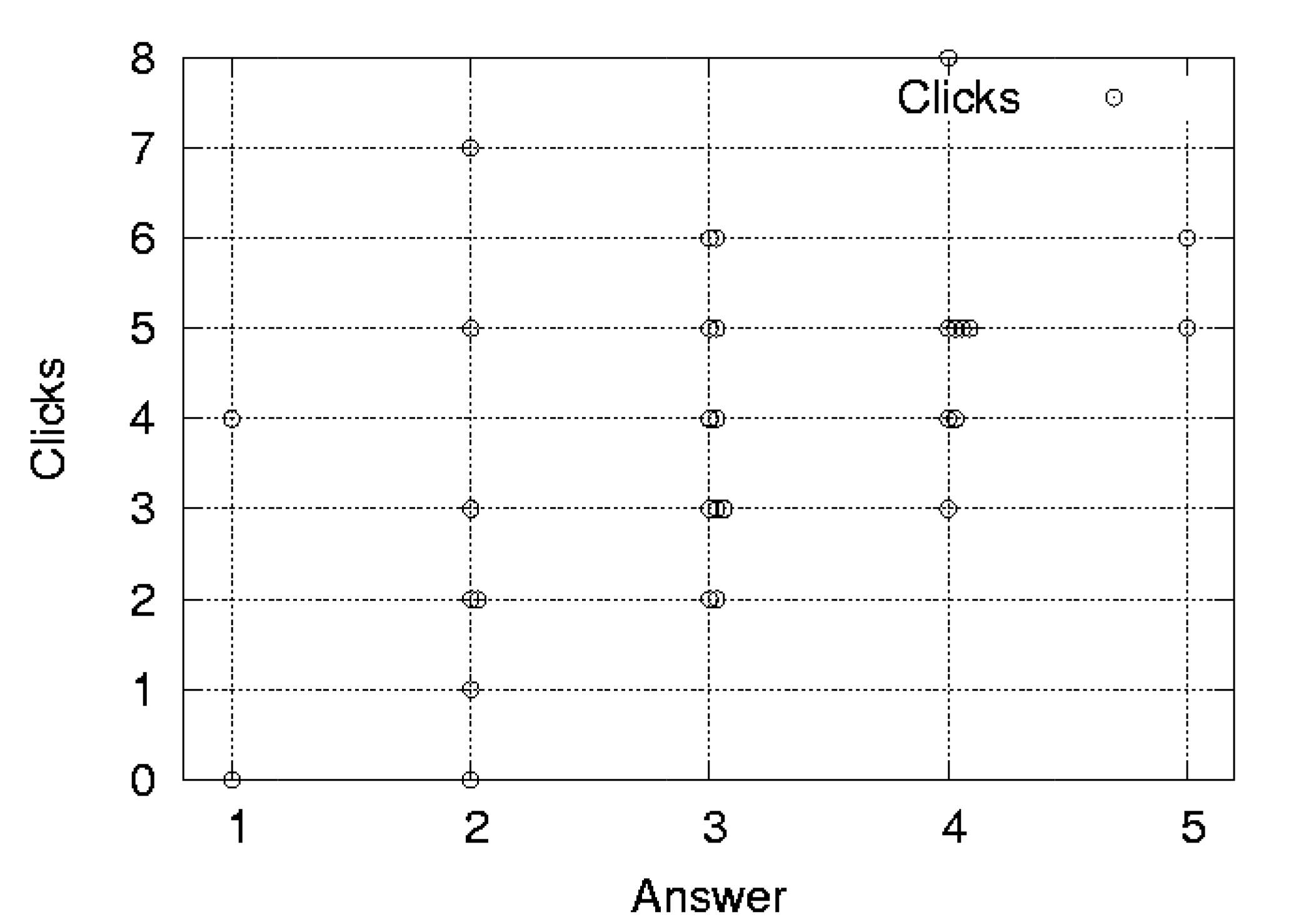
The relation of average-clicks and users' subjective distance is evaluated by questionnaires. We asked 13 participants to rank the pages according to their perceived familiarity. First we pick up 30 pages randomly within a few clicks from each participant's homepage. Then, we asked him/her to answer how familiar each URL of the page is, without providing the contents of the pages or any distance measures. Answers to the questions were made on a 5-point Likert-scale from 1 (very familiar) to 5 (very distant). After the questionnaires, we compare users' ratings with the distance by clicks/average-clicks.
Fig. 2 and 3 show the scatter plot of the results by participant 1. We can see clearly that the rating is correlated with the average-clicks measure. The correlation coefficients of 13 participants are shown in Table 4. Average-clicks have generally stronger correlation with the users' rating. In all the case, the correlation of clicks exceeds the correlation of average-clicks.
| Participant | Correlation coefficient | Significance level of difference |
|
|---|---|---|---|
| Clicks | Average-clicks | ||
| 1 | 0.524 | 0.836 | 1% |
| 2 | 0.325 | 0.804 | 1% |
| 3 | 0.471 | 0.685 | 5% |
| 4 | 0.268 | 0.572 | 5% |
| 5 | 0.641 | 0.674 | above 5% |
| 6 | 0.696 | 0.715 | above 5% |
| 7 | 0.517 | 0.699 | above 5% |
| 8 | 0.490 | 0.569 | above 5% |
| 9 | 0.499 | 0.528 | above 5% |
| 10 | 0.435 | 0.512 | above 5% |
| 11 | 0.358 | 0.436 | above 5% |
| 12 | 0.116 | 0.400 | above 5% |
| 13 | 0.302 | 0.367 | above 5% |
| Average | 0.434 | 0.600 | -- |
| Clicks | Average-clicks | |
|---|---|---|
| Understandability | -0.316 | -0.434 |
| Informativeness | 0.283 | 0.453 |
| Interestingness | -0.148 | -0.159 |
We made another questionnaire. Showing the participant the whole contents of the page for each 30 URL, we asked the following three questions:
Table 2 shows the average correlation coefficient of participants. Understandability has a negative correlation to the distance, that is, if the page is further, it gets more difficult to understand the contents. Informativeness has a positive correlation to the distance, and interestingness has almost nothing to do with distance. Understandability and informativeness have stronger correlation with the average-clicks than clicks measure. Average-clicks approximates the distance between the context of the participant homepage and the other page.
The Web is an example of a social network. Our research also reveals a part of a social network. In [4], the weight of a link is defined by referring to the text of the page. The average-clicks measure requires only the number of links.
The classical clicks measure is intuitively understandable for all Internet users, while the distance based on the probability is relatively difficult to understand. That's why we bring semantics by setting the base of the logarithm to the average number of links in a page: The distance shows how many "average clicks" are needed from one page to another page. This type of length (or cost) assignment is common in the context of cost-based abduction, where finding the MAP (maximum a posteriori probability) solution is equivalent to finding the minimal cost explanation for a set of facts [5]. Fetching the neighboring pages is a common procedure in many algorithms. Average-clicks measure provides a good justification of the practical search, such as "if there are few links, fetch the pages, but if there are many links, give up."
Our experiment is of course not conclusive, however we are convinced that at least in some cases we should use average-clicks instead of clicks measure.